Rep:Mod:01189257
NH3 optimization
Summary
| Question | Answer |
|---|---|
| What is the molecule? | Ammonia |
| What is the calculation method? | RB3LYP |
| What is the basis set? | 6-31G(d,p) |
| What is the final energy E(RB3LYP) in atomic units (au)? | -56.55776864 |
| What is the RMS gradient? | 0.00006917 |
| What is the point group of your molecule? | C3V |
Item
-- Stationary point found.
Item Value Threshold Converged?
Maximum Force 0.000075 0.000450 YES
RMS Force 0.000057 0.000300 YES
Maximum Displacement 0.000864 0.001800 YES
RMS Displacement 0.000399 0.001200 YES
Predicted change in Energy=-9.355400D-08
Optimization completed.
-- Stationary point found.
Bond lengths and angles
N-H bond length = 1.01811 Å
H-N-H bond angle = 105.706 °
Animation
Ammonia |
log file
Link: here
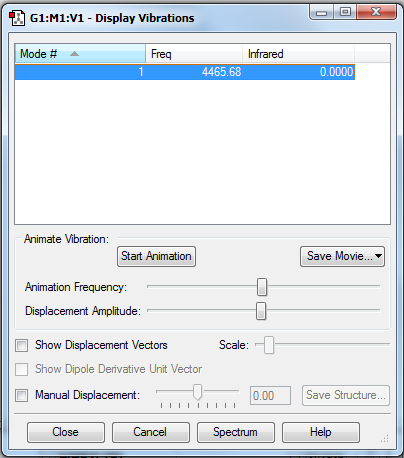
Vibrations
| Question | Answer |
|---|---|
| how many modes do you expect from the 3N-6 rule? | N = 4 hence 12 - 6 = 6 |
| which modes are degenerate (ie have the same energy)? | Modes 2 & 3 are degenerate and Modes 5 & 6 are degenerate. |
| which modes are "bending" vibrations and which are "bond stretch" vibrations? | Bending vibrations: 1, 2, 3
Stretching vibrations: 4, 5, 6 |
| which mode is highly symmetric? | 1, 4 |
| one mode is known as the "umbrella" mode, which one is this? | 1 |
| how many bands would you expect to see in an experimental spectrum of gaseous ammonia? | 2 |
Charges
Charge on N = -1.125 Charge on H = 0.375 Nitrogen, being the more electronegative element is expected to have a negative charge whereas Hydrogen is expected to have a positive charge.
N2 optimization
Summary
| Question | Answer |
|---|---|
| What is the molecule? | Nitrogen |
| What is the calculation method? | RB3LYP |
| What is the basis set? | 6-31G(d,p) |
| What is the final energy E(RB3LYP) in atomic units (au)? | -109.52412868 |
| What is the RMS gradient? | 0.00000060 |
| What is the point group of your molecule? | D∞H |
Item
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401001D-13
Optimization completed.
-- Stationary point found.
Vibrations
As the molecule is linear, by using the 3N - 5, the number of vibrational modes = 1 (symmetrical stretch). However, since this mode results in no change in dipole moment, there will be no bands on the experimental spectrum.
log file
Link: here
H2 optimization
Summary
| Question | Answer |
|---|---|
| What is the molecule? | Hydrogen |
| What is the calculation method? | RB3LYP |
| What is the basis set? | 6-31G(d,p) |
| What is the final energy E(RB3LYP) in atomic units (au)? | -1.17853936 |
| What is the RMS gradient? | 0.00000017 |
| What is the point group of your molecule? | D∞H |
Item
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
Vibrations
As the molecule is linear, by using the 3N - 5, the number of vibrational modes = 1 (symmetrical stretch). However, since this mode results in no change in dipole moment, there will be no bands on the experimental spectrum.
log file
Link: here
Haber-Bosch Process
| Parameter | Value |
|---|---|
| E(NH3) | -56.55776864 |
| 2*E(NH3) | -113.11553728 |
| E(N2) | -109.52412868 |
| E(H2) | -1.17853936 |
| 3*E(H2) | -3.53561808 |
| ΔE = 2*E(NH3)-[E(N2)+3*E(H2)] | -0.05579052 au = -146.47 kJ/mol |
Reaction is exothermic, hence favoured at low temperatures (Le Chatelier's Principle). However, this process is actually carried out at high temperature of 400 - 500 °C to strike a balance between rate of reaction and position of equilibrium.
Small molecule
Summary
| Question | Answer |
|---|---|
| What is the molecule? | Acrolein (systematic name: propenal) |
| What is the calculation method? | RB3LYP |
| What is the basis set? | 6-31G(d,p) |
| What is the final energy E(RB3LYP) in atomic units (au)? | -191.91801485 |
| What is the RMS gradient? | 0.00004031 |
| What is the point group of your molecule? | CS |
Item
Item Value Threshold Converged?
Maximum Force 0.000091 0.000450 YES
RMS Force 0.000032 0.000300 YES
Maximum Displacement 0.001406 0.001800 YES
RMS Displacement 0.000565 0.001200 YES
Predicted change in Energy=-7.295061D-08
Optimization completed.
-- Stationary point found.
Simulation
Acrolein |
Bond Lengths and Angles
C=O: 1.25840 Å
C-C: 1.54000 Å
C=C: 1.35520 Å
O=C-C: 120.227 °
C-C=C: 119.887 °
log file
Link: here
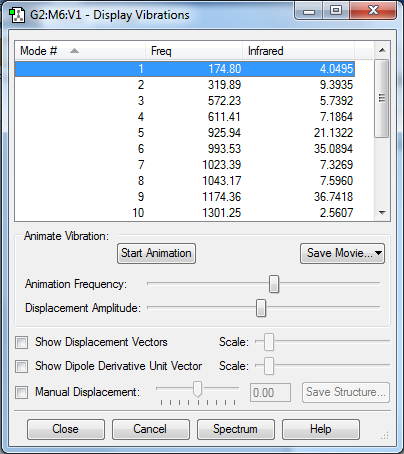
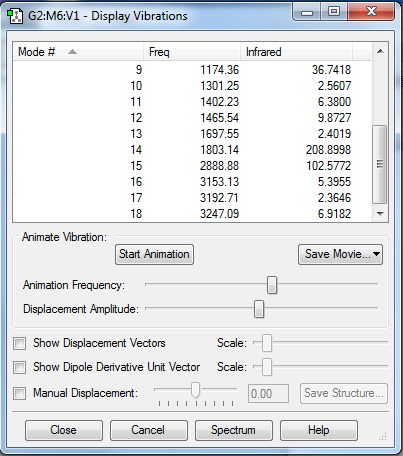
Vibrations
| Type | Modes |
|---|---|
| Bending modes | 1, 2, 5, 6, 7, 8 |
| Vibrating modes | 3, 4, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 |
By the 3N-6 rule for non-linear molecules, there are 18 vibrational modes.
Experimentally, there will likely be 5 peaks (all the other peaks may not be intense enough to show up on the experimental spectrum)
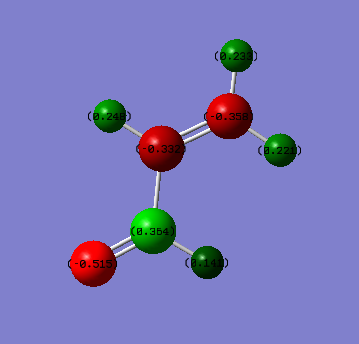
Charge distribution
Oxygen has the highest negative charge due its high electronegativity. Carbon of carbon has a slight positive charge as oxygen draws electron density away from it. α and β carbons have slight negative charge due to the alkene. The reason why the β has a larger negative charge than α carbon is that it is further away from oxygen.
Molecular Orbitals
HOMO
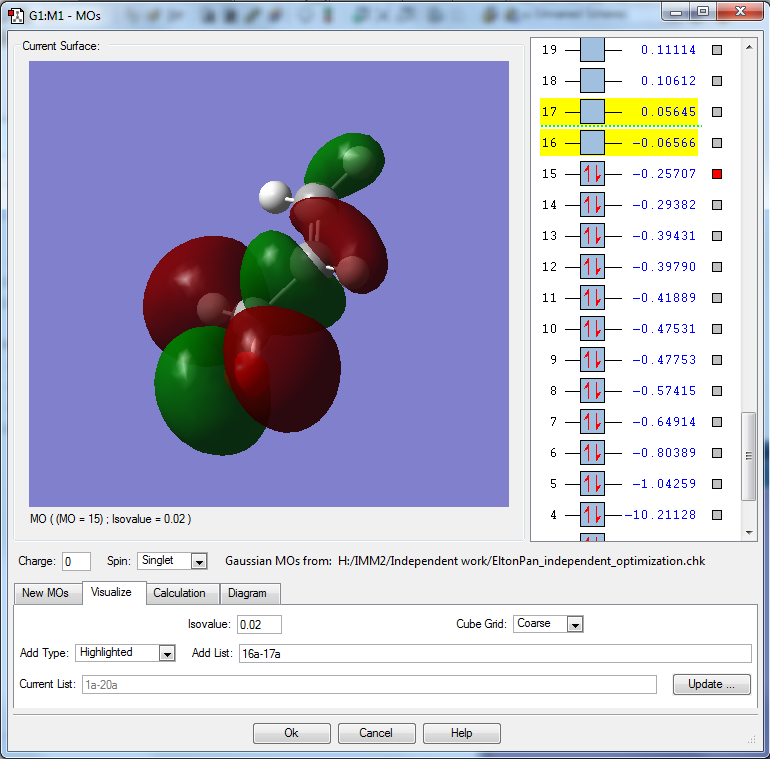
MO is constructed from the 2py & 2px of oxygen, 2py of carbonyl carbon, 2py of α carbon.
MO is bonding between α and β carbons but antibonding between oxygen and carbonyl carbon. Hence it is a mixture of bonding and antibonding.
This MO is the HOMO, having an energy of -0.25707 au, hence participates in reactions through the lone pair of the oxygen.
This MO is occupied, and contributes to the bonding within the alkene and within the carbonyl carbon and α carbon.
LUMO
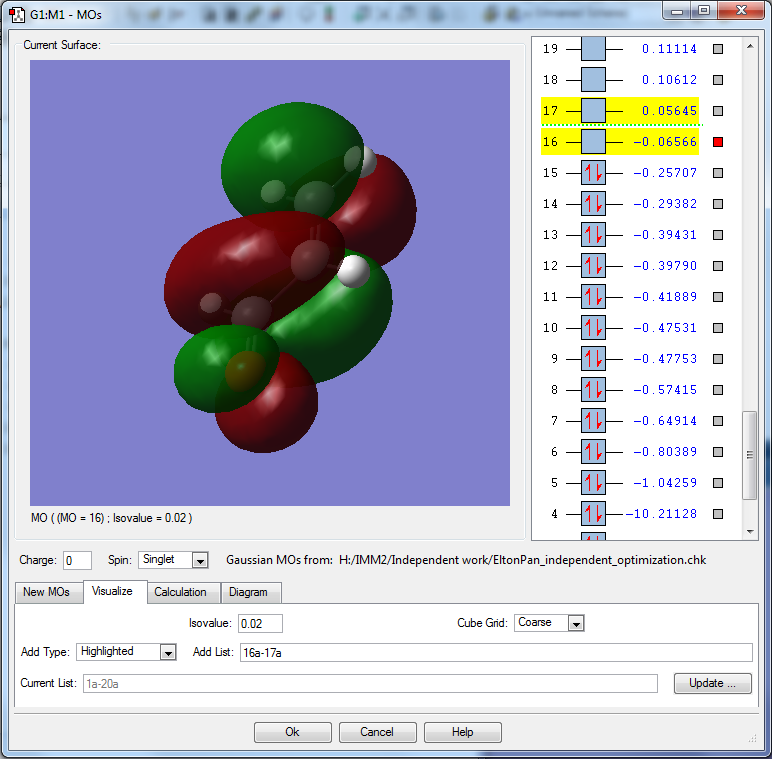
MO is constructed from overlap of 2pz and 3pz orbitals of 3 carbons and oxygen.
MO is bonding between carbonyl carbon and α carbons but antibonding between oxygen and carbonyl carbon.
It is also antibonding between α and β carbons. As a result of this, the LUMO is likely to react in a way such that C=O or C=C breaks (through 1,2- or 1,4- addition). Hence it is a mixture of bonding and antibonding.
This MO is the LUMO, having an energy of -0.06566 au, hence is in the range of energy to participate in reactions.
This MO is unoccupied, and hence can accept electrons in direct or Michael addition reactions. [1]
Other MOs
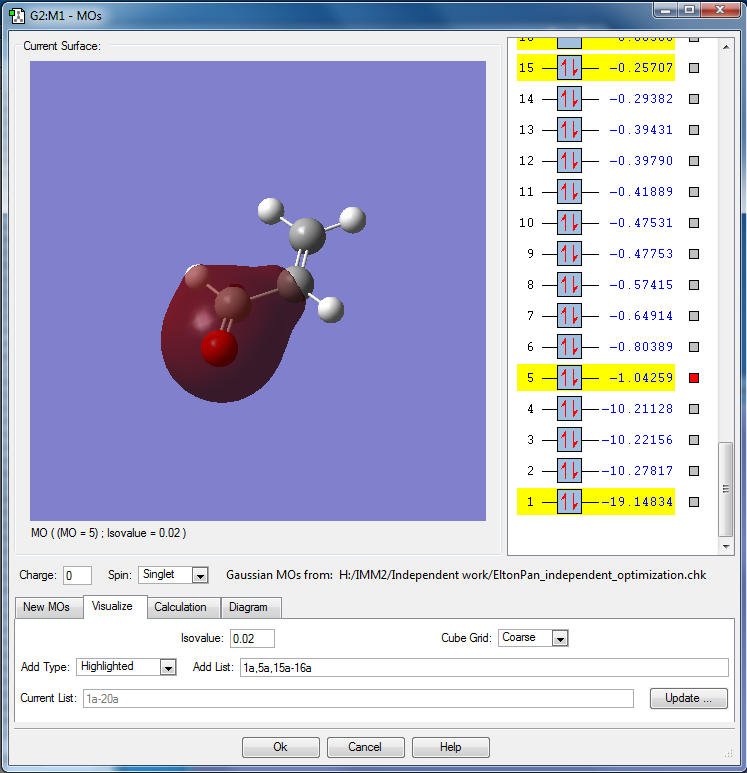
MO is constructed from 2s of oxygen, 2px of carbonyl carbon and 2py, 2s of α carbon.
This results in a bonding MO.
This MO is relatively deep in energy, as it is around 0.79 au deeper in energy compared to the HOMO.
This MO is occupied, and contributes to the bonding carbonyl the α carbon.
MO is constructed from constructive overlap of 2p orbitals of 3 carbons and oxygen.
This results in a bonding MO.
This MO is relatively deep in energy, as it is around 0.14 au deeper in energy compared to the HOMO.
This MO is occupied, and contributes to the bonding between all 4 atoms (3C and 1O).
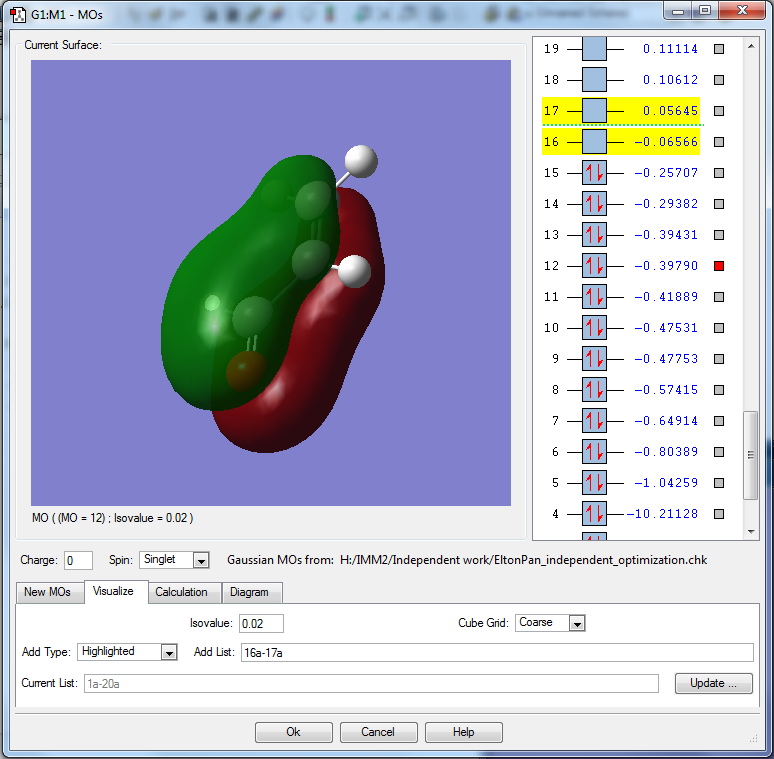
MO is constructed from the 2pz orbitals of the α and β carbons. It also consists of 2p of oxygen and carbonyl carbon.
MO is bonding between α and β carbons. MO is bonding between oxygen and carbonyl carbon. However, it is antibonding between carbonyl carbon and α carbon. Hence, it is a mixture of bonding and antibonding.
This MO is relatively deep in energy, as it is around 0.79 au deeper in energy compared to the HOMO.
This MO is occupied, and contributes to the bonding within the carbonyl and within the alkene.
Independence
The extension that was carried out was the orbital contributions (which AOs make up a given MO) as described above were obtained by looking at the molecular orbital coefficients detailed in the .log file of acrolein, a relatively more complicated molecule.
References
- ↑ Michael, A. (1887), Ueber die Addition von Natriumacetessig- und Natriummalonsäureäthern zu den Aethern ungesättigter Säuren. J. Prakt. Chem., 35: 349–356. doi:10.1002/prac.18870350136