Rep:Mod:01188093

NH₃

Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -56.55776873 au
RMS Gradient: 0.00000485 au
Point Group: C3V
N-H Bond Distance: 1.01798 Å
H-N-H Bond Angle: 105.741°

Item                     Value        Threshold   Converged?
Maximum Force            0.000004     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000072     0.001800     YES
RMS     Displacement     0.000035     0.001200     YES

NH3

The optimisation file is liked to here

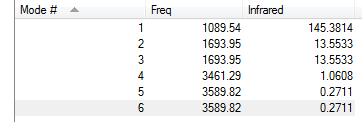
Expected Modes:6
Degenerate: Modes 1 and 2, Modes 5 and 6
Bending Modes: 1,2,3
Stretching Modes: 4,5,6
Highly Symmetric: 4
"Umbrella" Mode: 1
No. of Expected Bands in Spectra: 2; only asymmetric stretches show up in IR spectrum
as they involve a change in dipole moment and as such mode 4 will not appear. Mode 5 
and 6 have a very weak intensity and as such will most likely be buried by noise. Thus,
only modes 1, 2 and 3 will show up and as 2 and 3 are degenerate this will present
itself as only two bands


Expected: Negative on the N and Positive on the H
Charge on N: -1.125
Charge on H: 0.375

N₂

Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -109.52412868 au
RMS Gradient: 0.00000060 au
Point Group: D∞h
N-N Bond Distance:  1.10550 Å

Item                     Value        Threshold    Converged?
Maximum Force            0.000001     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000000     0.001200     YES

N2

The optimisation file is liked to here

H₂

Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -1.17853936 au
RMS Gradient: 0.00000017 au
Point Group: D∞h
H-H Bond Distance:  0.74279 Å

Item                     Value        Threshold    Converged?
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000001     0.001200     YES

H2

The optimisation file is liked to here

The Haber-Bosch Process

N₂ + 3H₂ -> 2NH₃

E(NH3)= -56.55776873 au
2*E(NH3)= -113.11553746 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au 
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579070 au
                           = -146.47848290 kJ/mol

Literature Value: ΔH = -45.7 kJ/mol

The literature value is for the reaction at standard conditions to produce one mole of ammonia.
Thus, the literature value is -91.4 kJ/mol which is quite close to the value calculated by using computational 
chemistry which is expected as there are experimental considerations that would affect the value calculated.
The ammonia product is more stable as the reaction is exothermic.

F₂

Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -199.49825218 au
RMS Gradient: 0.00007365 au
Point Group: D∞h
F-F Bond Distance: 1.40281 Å

Item                     Value        Threshold    Converged?
Maximum Force            0.000128     0.000450     YES
RMS     Force            0.000128     0.000300     YES
Maximum Displacement     0.000157     0.001800     YES
RMS     Displacement     0.000221     0.001200     YES


Expected: Charge Density to be zero for both F as homodinuclear molecule
Charge on F: 0.000

F2

The optimisation file is liked to here

Molecular Orbitals

This orbital comes from the overlap of the 2s orbitals on the F atoms when the 
orbitals are in phase. The MO is bonding there is constructive 

This orbital comes from the overlap of the 2s orbitals on the F atoms when the 
orbitals are out of phase. The MO is anti-bonding as there is destructive 
interference thus resulting in the lack of electron density between the two atoms

This orbital comes from the overlap of the 2p orbitals on the F which lie along 
the axis of the bond. The MO is thus a sigma bond as it is formed by two 
orbitals interacting head on. It is a bonding orbital as there is constructive 
interference between the two atoms.

This orbital comes from the overlap of the 2p orbitals on the F which lie 
perpendicular to the axis of the bond. The MO is a pi bond and it is a bonding 
orbital as the two lobes are in phase with the corresponding lobes on the other 
atom. There is constructive interference and hence electron density between the atoms. 

This orbital comes from the overlap of the 2p orbitals on the F which lie 
perpendicular to the axis of the bond. The MO is a pi bond and it is an anti bonding 
orbital as the two lobes are out of phase with the corresponding lobes on the other 
atom and thus there is destructive interference. This is the HOMO as it is the MO 
with the highest energy while still filled. The LUMO is the 3σ* orbital.