Rep:Mod:01053372
NH3 Molecule
General Analysis
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -56.55776873 a.u |
| RMS Gradient | 0.00000485 |
| Point Group | C3V |
| NH Bond Distance | 1.01798Å |
| HNH Bond Angle | 105.741° |
"Item" Table:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986270D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
test molecule |
Frequency Analysis
Display Vibrations Table:
Q) How many modes do you expect from the 3N-6 rule? (3*4)-6 = 6
Q) Which modes are degenerate (ie have the same energy)? Modes 2&3 and 5&6
Q) Which modes are "bending" vibrations and which are "bond stretch" vibrations? 1,2&3 are bending vibrations. 4,5&6 are stretching vibrations.
Q) which mode is highly symmetric? 4
Q) One mode is known as the "umbrella" mode, which one is this? 1
Q) How many bands would you expect to see in an experimental spectrum of gaseous ammonia? 4
Charge Analysis
Atomic Charge: I would expect the N atom to be more negatively charged, seeing as it is more electronegative than Hydrogen.
N-atom has a charge of -1.125
H-atom has a charge of +0.375
The Haber-Bosch Process
The Haber–Bosch process converts atmospheric nitrogen to ammonia by a reaction with hydrogen with a metal catalyst and high temperatures and pressures:
N2 + 3H2 → 2 NH3
N2
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -109.52359111 a.u |
| RMS Gradient | 0.02473091 |
| Point Group | D∞h |
| Imaginary Freq | 0 |
| Dipole Moment | 0 |
"Item" Table:
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401161D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Vibrations: 1) 2457.33 (Not IR active)
test molecule |
H2
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -1.17853936 a.u |
| RMS Gradient | 0.00000017 |
| Point Group | D∞h |
| Imaginary Freq | 0 |
| Dipole Moment | 0 |
"Item" Table:
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Vibrations: 1) 4465.68 (Not IR active)
test molecule |
The Reaction
E(NH3)= -56.55776873
2*E(NH3)= -113.11553746
E(N2)= -109.52359111
E(H2)= -1.17853936
3*E(H2)= -3.53561808
ΔE= 2*E(NH3)-[E(N2)+3*E(H2)]= -113.11553746 - (-109.52359111 + -3.53561808) = -0.05632827 a.u
Therefore the energy released when converting hydrogen and nitrogen gas to ammonia is, ΔE= -147.889884151 kJ/mol. This would suggest the ammonia product is more thermodynamicaly stable.
The literature value for the enthalpy change of the formation of one mole of gaseous ammonia is −46.1 kJ/mol, so for two moles this would be -96.2kJ/mol.[1]. This was much lower than my modeled reaction and highlights the limits of calculating energy changes of even simple reactions by purely theoretical means. The difference may be due to the fact that the experimental literature value is a enthalpy change, and in our theoretically modeled value we made no assumptions about the pressure, or temperature of the system.
Project Molecule
General Analysis
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -291.88802549 a.u |
| RMS Gradient | 0.00023228 |
| Point Group | Td |
| Si-H-Si Angle | 109.471° |
| Si-H Bond Length | 1.48609Å |
"Item" Table:
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-2.454553D-14
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4849 -DE/DX = 0.0 !
! R2 R(1,3) 1.4849 -DE/DX = 0.0 !
! R3 R(1,4) 1.4849 -DE/DX = 0.0 !
! R4 R(1,5) 1.4849 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
test molecule |
Frequency Analysis
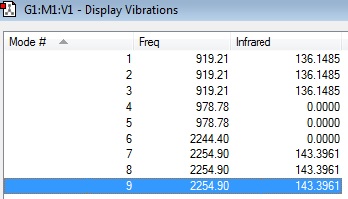
Frequency Table:
Modes 1,2&3 are degenerate bends, wich are IR active. Modes 4,5 are degenerate bends which are IR inactive. Mode 6 is a symmetric stretch which is IR inactive. Modes 7,8 & 9 are degenerate stretches which are IR active.
the 3N-6 rule predicts 9 modes of vibration, corroborating our calculations. However due to the degeneracy and IR inactivity we would expect to see 2 bands in an experimental spectrum of gaseous Silane (modes 1,2&3 and modes 7,8&9).
IR Spectra
Modeled Spectra:
Literature Spectra:
From the experimental literature spectra of Silane we can see a vibrational absorption a little above 2200 wavenumbers, which corresponds to our theoretically calculated 2254.90 wavenumbers. this suggests our model of Silane's bond strenghts and lengths is accurate.
Charge Analysis
Seeing as Hydrogen is more electronegative than Silicon (With Pauling electronegativities of 2.2 and 1.9 respectively) I would expect the Silicon to be positively charged and Hydrogen negatively charged.
Silicon Charge: +0.629
Hydrogen Charge: -0.157
MO Analysis
MO1
Energy: -66.12596 a.u, This is extremely deep in energy which would suggest the Orbital originates from a core AO
Contributing AOs: Si 1s
Bondng type: Non-bonding. The orbital is too low in energy to contribute to bonding
Occupancy: An electron pair
MO2
Energy: -5.28056 a.u, This orbital is lower in energy compared to the HOMO/LUMO energies.
Contributing AOs: Si 2s
Bondng type: Non-bonding. The orbital is too low in energy to contribute to bonding
Occupancy: An electron pair
MO3
Energy: -3.63858 a.u, This orbital is lower in energy compared to the HOMO/LUMO energies.
Contributing AOs: Si-2p
Bondng type: Non-bonding Orbital, this does not contributes to the overall bonding in the molecule as it is too low in energy to interact with the H-1s orbitals
Occupancy: An electron pair
MO9
Energy: -0.35184 a.u, This is the HOMO.
Contributing AOs: A linear subtraction of the Si-3px and Si-3py produces a p like orbital in the diagonal. This combines with 4 H-1s orbitals (in phase with the lobe of the p orbital there interacting with).
Bondng type: Bonding Orbital, this contributes to the overall bonding in the molecule.
Occupancy: An electron pair
MO10
Energy: 0.05053 a.u, This is the LUMO.
Contributing AOs: A linear subtraction of the Si-3px and Si-3py produces a p like orbital in the diagonal. This combines with 4 H-1s orbitals (out of phase with the lobe of the p orbital there interacting with).
Bondng type: Antibonding, detracts from the overall bonding in the molecule. However in this case the orbital is unoccupied
Occupancy: unoccupied
References
- ↑ http://www.chemguide.co.uk/physical/equilibria/haber.html, accessed at 23/2/17 11:24am
- ↑ J. Am. Chem. Soc., 2003, 125 (21), pp 6581–6587, DOI: 10.1021/ja029862l