Rep:Mod:00636773Phys

In this project, results are given as links to anchors in a separate page.

Introduction

The Cope Rearrangement

The Cope rearrangement is a special case of a pericyclic reaction, more specifically a [3,3] sigmatropic intramolecular rearrangement. Following the general scheme for 1,5-hexadiene:

It can also be viewed as being a biradical reaction, with a transition state:

This can go via a boat-like conformation (top) or a chair-like conformation (below):

In this exercise, the rearrangement of 1,5-hexadiene was investigated through various operations - some conformers were optimised to a minimum and a transition state. The transition states were calculated through QST2, QST3 and using the Berny algorithm. These were then used to confirm reactants and products via IRC calculations, and the activation energies were measured.

Additionally, an analogue of 1,5-hexadiene, cis-1,2-divinylcyclobutane was calculated as above and briefly mentioned.

The Diels Alder Reaction

The Diels Alder reaction is the cycloaddition reaction of a diene with a dienophile. The dienophile typically contains a conjugated electron withdrawing group.

In this exercise, the reaction coordinates were calculated for pairs ethylene/cis-butadiene, maleic anhydride/cyclohexa-1,3-diene, sulfur dioxide/butadiene, and sulfur dioxide/1,3-bismethylene cyclohexane.

The Cope Rearrangement

The Cope Rearrangement reaction coordinate was calculated on Gaussian. First, the reactants/products were optimised. Transition state were guessed and optimised, and quadratic synchronous transit calculations were used to predict which products the transition states decomposed to. The energy difference was recorded as the activation energy.

Optimising the Reactants and Products

Some conformations of 1,5-hexadiene were optimised to get used to the exercise. Their relative energies were taken to get an idea of the stabilisation and steric energies involved. Although it might seem that anti conformers would have a lower energy than gauche conformers, Gauche3 was found to have the lowest due to its compromise between steric hindrance and favourable Van der Waals interactions.

Property:	Linkage:
Property:	Anti2:			Gauche5:	Gauche3:
Basis Set:	3-21G	6-31G(d) Opt	6-31G(d) Freq	3-21G	3-21G
Energy:	-231.69253530 a.u.	-234.61171035 a.u.	-234.61171035 a.u.	-231.68961573 a.u.	-231.69266121 a.u.
Relative Energy:	+0.00012591 a.u. +0.33 kJ•mol^-1 +0.08 kcal•mol^-1			+0.00304548 a.u. +8.00 kJ•mol^-1 +1.98 kcal•mol^-1	+0 a.u.
Point Group:	C_i/C₁	C_i/C₁	C_i/C₁	C₁	C₁

The geometry is not affected much between the basis sets 3-21G and 6-31G, as they both minimise energies and converge to similar structures. However, these minima are different to each other and cannot be compared. The anti2 is noted to have a centre of inversion.

Some of the thermochemistry data for the 6-31G basis set of the anti2 confomration is given below:

Anti2
Sum of electronic and zero-point energies:	-234.469204 a.u.
Sum of electronic and thermal energies:	-234.461857 a.u.
Sum of electronic and thermal enthalpies:	-234.460913 a.u.
Sum of electronic and thermal free energies:	-234.500777 a.u.

Optimising the "Chair" and "Boat" Transition Structures

The transition states were guessed and optimised using both the 3-21G and the 6-31G basis sets. Quadratic Synchronous Transits were used with the "reactant" and "product" (QST2), and then with an additional "transition" structure (QST3).

Transition State Structure

An allyl group (radical) was optimised and duplicated to produce, approximately, either a boat or a chair transition state. These transition state structures were further optimised using the Berny algorithm.

Three tries were made - one was a direct optimisation, the second was a failed attempt at freezing coordinates (in retrospect, it's unsurprising that modifying one bond length changes the bond length of another in a cyclic system, all else constant).

Property:	Molecule:
Property:	Allyl:	Chair TS 1:		Chair TS 2:		Chair TS 3:
Type:	Opt	Opt	Freq	Frozen 1	Derivative 1	Frozen 2	Derivative 2	Freq. Analysis 2
Energy:	-115.82304010 a.u.	-231.61932244 a.u.	-231.61932244 a.u.	-231.61402414 a.u.	-231.61932239 a.u.	-231.61517051 a.u.	-231.61932233 a.u.	-231.61932196 a.u.
Imaginary Frequency:			-817.92 cm^-1					-817.99 cm^-1
Bond Lengths (forming/breaking):		2.02Å/2.02Å		2.26Å/2.21Å	2.02Å/2.02Å	2.20Å/2.20Å	2.02Å/2.02Å

The negative frequency was visualised and corresponded to the expected bond-forming/-breaking mode. This is important to confirm the transition state as it represents the local maximum of the particular reaction coordinate.

QST2 and QST3

In the first QST2 calculation, Gaussian successfully broke the structure into two allyl fragments, but then translated one on top of the other. In doing this is creates nearly a chair transition state, but considers the opposite carbons bonded. Simply rotating the central dihedral slightly to break the symmetry was not sufficient to produce the correct structure.

In the second QST2 calculation, the geometry was forced to be similar to the boat transition state. In this case, the boat transition state was successfully found.

In the QST3 calculation, by giving a guessed transition state, Gaussian also successfully optimised a transition state.

Property:	Molecule:
Property:	QST2:		QST3:
Type:	Chair (Failed)	Boat	Boat
Energy:	-231.61932241 a.u.	-231.60280243 a.u.	-231.60280235 a.u.
Imaginary Frequency:	-817.96 cm^-1	-840.18 cm^-1	-840.10 cm^-1
Bond Lengths (forming/breaking):	2.02Å/2.02Å	2.14Å/2.14Å	2.14Å/2.14Å

Attempting to find a boat transition state from anti2 yielded a near-chair transition state
A more rigorous approach successfully found the boat transition state

Intrinsic Reaction Coordinate Calculations

IRC calculations were performed on the optimised transition states. This pushes the the reaction coordinate down the steepest gradient and in the opposite direction (if specified) until a minimum is reached, or the given number of steps is reached. This generates a set of reactants and products. In this case, the reactants and products are identical, and so the IRC is symmetric. The product was optimised and an activation energy was calculated for each set.

		Conformation:
		Boat			Chair
		3-21G:	6-31G(d):	Experimental:	3-21G:	6-31G(d):	Experimental:
Transition State:	Electronic Energy:	-231.60280243 a.u.	-234.54309345 a.u.		-231.61932239 a.u.	-234.55698311 a.u.
	Sum of Electronic and Zero-Point Energies:	-231.460431 a.u.	-234.402347 a.u.		-231.470142 a.u.	-234.414932 a.u.
	Sum of Electronic and Thermal Energies:	-231.454364 a.u.	-234.396012 a.u.		-231.464434 a.u.	-234.409011 a.u.
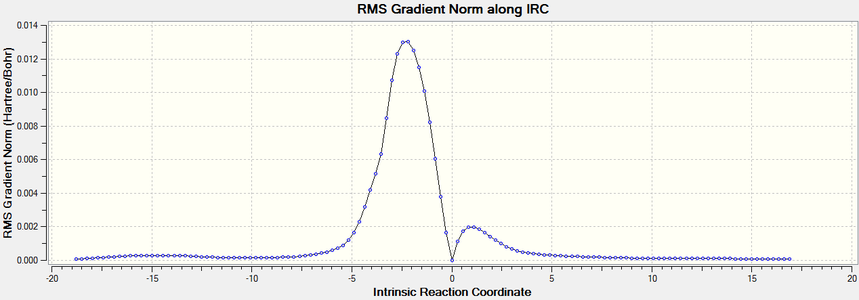
	IRC:
Product:	Electronic Energy:	-231.69266122 a.u.	-234.61132934 a.u.		-231.69253530 a.u.	-234.61171035 a.u.
	Sum of Electronic and Zero-Point Energies:	-231.539486 a.u.	-234.468693 a.u.		-231.538704 a.u.	-234.468263 a.u.
	Sum of Electronic and Thermal Energies:	-231.532647 a.u.	-234.461464 a.u.		-231.531794 a.u.	-234.460957 a.u.
	Conformation:	Gauche3			Anti2
Activation Energy:	0K:	0.079055 a.u.	0.066346 a.u.		0.068562 a.u.	0.053331 a.u.
		207.56 kJ·mol^-1	174.19 kJ·mol^-1		180.01 kJ·mol^-1	140.02 kJ·mol^-1
		49.61 kcal·mol^-1	41.63 kcal·mol^-1	44.7±2.0 kcal·mol^-1 ^[1]	43.02 kcal·mol^-1	33.47 kcal·mol^-1	33.5±0.5 kcal·mol^-1 ^[1]
	298.16K:	0.078283 a.u.	0.065452 a.u.		0.067360 a.u.	0.051946 a.u.
		205.53 kJ·mol^-1	171.84 kJ·mol^-1		176.85 kJ·mol^-1	136.38 kJ·mol^-1
		49.17 kcal·mol^-1	41.07 kcal·mol^-1		42.27 kcal·mol^-1	32.60 kcal·mol^-1

As seen above, 6-31G produces a more accurate result when compared to experimental data. This could be that the basis set reproduces the transition state more accurately reducing the energy, and thus the activation energy is lower.

Creating Cycloocta-1,5-diene

By tethering two of the bonding carbons with an ethylene group, producing a cyclobutane, the product would be cycloocta-1,5-diene^[2]. In this section, the chair conformation equivalent was used.

The transition state was located using the Berny algorithm and an IRC calculation was performed to confirm this and generate reactants and products, which were then optimised.

IRC showing reactants on the right, products on the left.
A gradient plot of the IRC.

Property:	Molecule:
Property:	cis-1,2-Divinylcyclobutane:	Transition State:	Cycloocta-1,5-diene:
Energy:	0.06341935 a.u.	0.11529254 a.u.	0.04274677 a.u.
Relative Energy:	0.00 a.u. 0.00 kJ·mol^-1	+0.05187319 a.u. +32.55 kcal·mol^-1	-0.02067258 a.u. -12.97 kcal·mol^-1

An activation energy of 32.55 kcal·mol^-1 and a change of free energy of -12.97 kcal·mol^-1 were calculated.

The Diels Alder Cycloaddition

Ethylene and cis-Butadiene

The Berny TS (intramolecular bond lengths were made equivalent and the intermolecular distances were 2.2Å) was found for the Diels Alder reaction of ethylene and cis-Butadiene using AM1 and ZDO basis sets. an IRC calculation was then performed and the reactants and products were then optimised. An activation energy of 23.01 kcal·mol^-1 and a change of free energy of -53.96 kcal·mol^-1 were calculated.

Property:	Molecule:
Property:	Ethylene:	cis-Butadiene:	Ethylene + cis-Butadiene (infinite displacement):	Ethylene + cis-Butadiene (Van der Waals displacement):	Transition State:	Product:
Energy:	0.02619024 a.u.	0.04879717 a.u.	0.07498741 a.u.	0.07462794 a.u.	0.11165465 a.u.	-0.01099616 a.u.
Relative Energy:			0.00000000 a.u. 0 kcal·mol^-1	-0.00035947 a.u. -0.23 kcal·mol^-1	+0.03666724 a.u. +23.01 kcal·mol^-1	-0.08598357 a.u. -53.96 kcal·mol^-1
Imaginary Frequency:					-956.22 wavenumbers

MO Analysis

The MOs were plotted and placed in the same orientation. The transition state had one plane of anti-symmetry, as shown cutting through the screen vertically. The relative energies are given, followed by symmetry (a=antisymmetric, s=symmetric) and wavefunction.

Molecule:	Orbital:
Molecule:	HOMO	LUMO
Ethylene:	-0.37969 s φ_{Ethylene HOMO}=φ_HOMO(E)	0.18661 a φ_{Ethylene LUMO}=φ_LUMO(E)
cis-Butadiene:	-0.32539 a φ_{cis-Butadiene HOMO}=φ_HOMO(B)	0.12365 s φ_{cis-Butadiene LUMO}=φ_LUMO(B)
Transition State:	-0.32394 a ψ₂=φ_HOMO(B)+φ_LUMO(E)	0.02315 s ψ₃=φ_LUMO(B)-φ_HOMO(E)
Transition State:	-0.32499 s ψ₁=φ_LUMO(B)+φ_HOMO(E)	0.33780 a ψ₄=φ_HOMO(B)-φ_LUMO(E)
Product:	-0.34187 a ψ_{Cyclohexene HOMO}	0.19311 s ψ_{Cyclohexene LUMO}

The intermolecular bond lengths were 2.12Å, significantly longer than typical sp³-sp³ (1.53-1.55Å), sp³-sp² (1.49-1.52Å) and sp²-sp² (1.45-1.48Å) C-C bond lengths^[3], suggesting that no formal bonding takes place in the transition state.

The orbitals of ethylene and cis-butadiene combine when their symmetries and phases match and overlap favourably, and are thus symmetry allowed. This produces four MOs for the transition state, given by the addition or subtraction of the ethylene and cis-butadiene orbitals. The HOMO for the TS was antisymmetric, suggesting it is formed from the LUMO of ethylene and the HOMO of butadiene.

A close inspection of the energy levels reveals no significant lowering of energy between the transition state and product energies. However, bonding as well as non-bonding orbital interactions across all the MOs will shift in such a way as to lower the overall energy of the product. This shows that often it is insufficient to look at just the HOMO and LUMO.

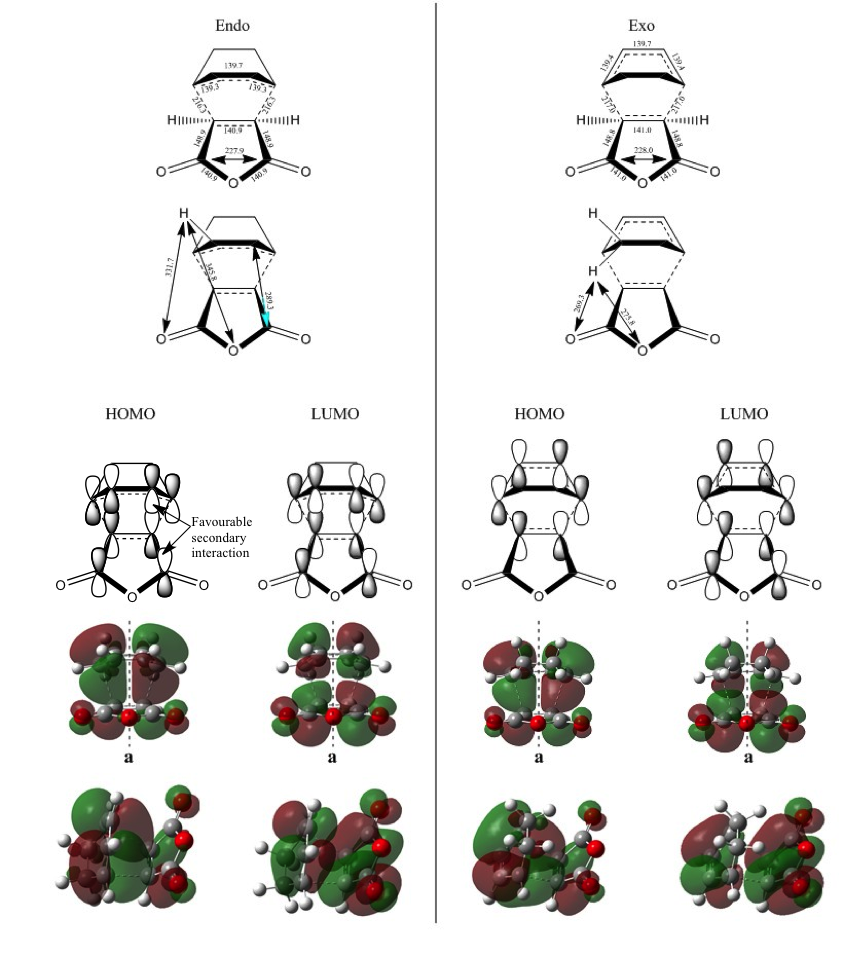
Maleic Anhydride and Cyclohexa-1,3-diene

IRC calculations were performed for the endo and exo transition states for the reaction of maleic anhydride and cyclohexa-1,3-diene and the reactants and products were optimised using AM1 and a ZDO basis set. It was found that the IRC would crash unless the 'Recorrect' option was set to 'Never'. The endo transition state had a lower activation energy, corresponding to about 80% endo and 20% exo.

Property:		Molecule:
Property:		Maleic Anhydride:	Cyclohexa-1,3-diene:	Reactants (infinite displacement):	Transition State:		Product:
Endo:	Energy:	-0.12182424 a.u.	0.02771128 a.u.	-0.09411296 a.u.		-0.05150477 a.u.	-0.16017085 a.u.
	Relative Energy:			0.00000000 a.u. 0 kcal·mol^-1		+0.04260819 a.u. +26.73 kcal·mol^-1	-0.06605789 a.u. -41.45 kcal·mol^-1
	Imaginary Frequency:					-806.05 wavenumbers
Exo:	Energy:	-0.12182424 a.u.	0.02771128 a.u.	-0.09411296 a.u.		-0.05041949 a.u.	-0.15990941 a.u.
	Relative Energy:			0.00000000 a.u. 0 kcal·mol^-1		+0.04369347 a.u. +27.42 kcal·mol^-1	-0.06579645 a.u. -41.29 kcal·mol^-1
	Imaginary Frequency:					-812.18 wavenumbers

MO Analysis

Below are the MOs showing the dependence of kinetics on the approach of cyclohexa-1,3-diene. The approach can be visualised as coming from above and into the page.

Looking at the geometry and MOs of the endo and exo approaches and the transition states, it can be justified that not only does the H<->O distance slightly intrude on their combined Van der Waals radii (275pm), but there is a secondary, non-bonding interaction in the HOMO of the endo transition that lowers the energy, making it more accessible and kinetically favourable. All distances are given in picometres.

As with ethylene and cis-butadiene, the bond lengths were significantly longer than usual, and again it was concluded that no formal bonding took place in the transition state. Both TS HOMOs are antisymmetric, being formed from the LUMO of maleic anhydride and the HOMO of cyclo-1,3-hexadiene.

Hetero-Diels Alder

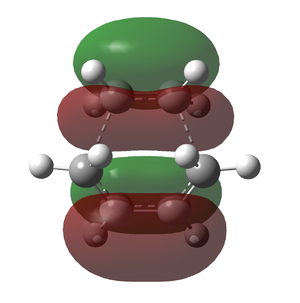
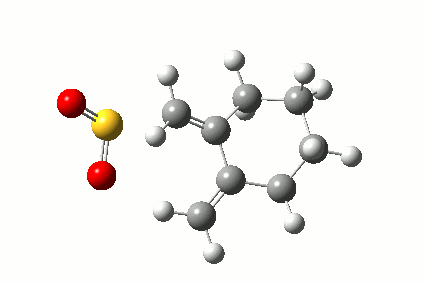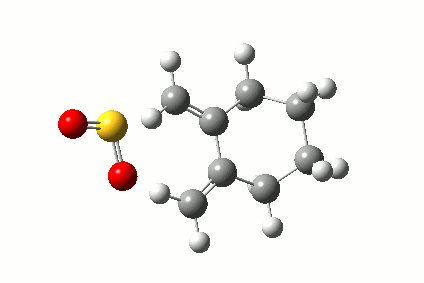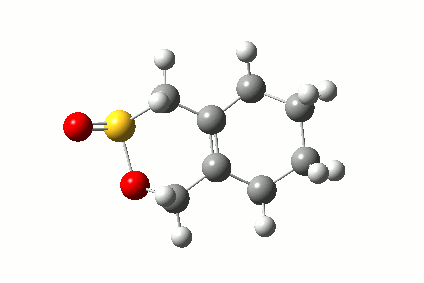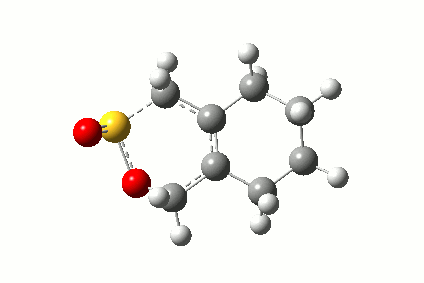
Breaking away from C-C forming reactions, Diels Alder reactions occur for other atoms, including nitrogen and in this case, sulfur and oxygen^[4]. IRC results were plotted for the reaction of sulfur dioxide and cis-butadiene, and sulfur dioxide and 1,2-bismethylene cyclohexane to produce their respective sultines.

Sulfur dioxide and cis-butadiene:

SO₂ + C₄H₆ ⇋ C₄H₆SO₂
The IRC plot of the above reaction.
The gradient of the IRC plot

Sulfur dioxide and 1,2-bismethylene cyclohexane:

SO₂ + C₈H₁₄ ⇋ C₈H₁₄SO₂
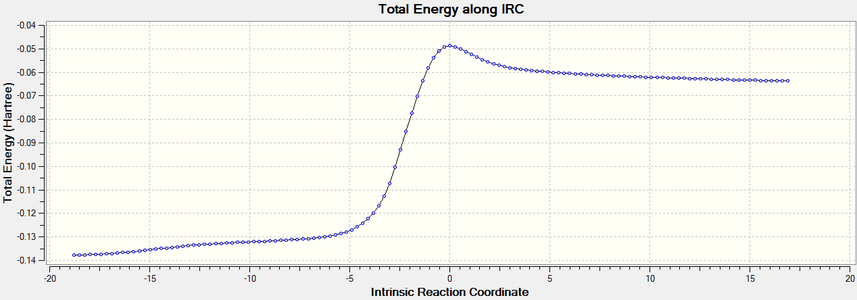
The IRC plot of the above reaction.
The gradient of the IRC plot

Using AM1 and a ZDO basis set, a barrier of 9.06 kcal·mol^-1 was calculated, with a change of energy of -44.99 kcal·mol^-1 for the cis-butadiene, and 9.38 kcal·mol^-1 and -46.46 kcal·mol^-1 for 1,2-bismethylene cyclohexane. While the barriers are similar for each case, the fact that the butadiene is locked in the cis position for the 1,2-bismethylene cyclohexane means more reactant is available, increasing the rate by removing a pair of rate steps from the equation.

A competing cheletropic reaction was also observed for the 1,2-bismethylene cyclohexane that generated the sulfolene. The energy barrier was significantly greater(37.45 kcal·mol^-1), while the change of free energy was also greater(-67.92 kcal·mol^-1). This suggests the sultine is the kinetic product and the sulfolene is the thermodynamic product.

MO Analysis

Looking at the computed MOs for the reactants, it is apparent that SO2 has roughly the correct symmetries to undergo a Diels-Alder reaction. The approach angle is from top-down and into the page, and the phase of the SO₂ HOMO were inverted.

Conclusions

Basis sets and methods

6-31G(d) produces lower energy values than 3-21G, and reproduces experimental data more accurately.
AM1 is much faster than 6-31G(d) and 3-21G, while producing reasonably accurate results.

Transition States

Often QST2 is not sufficient to locate a transition state, as it takes a line through the reaction coordinate, which can lead to the wrong TS.
Given a good geometry, the Berny TS algorithm is effective.

IRC

IRC calculations are useful in proving the TS is correct. It yields a set of reactants and products that can be optimised.
IRC plots can be made to visualise the reaction.

MO Analysis

MO Analysis can be performed to check whether a reaction is symmetry forbidden or allowed.
Sometimes it is not sufficient to simply look at the HOMOs and LUMOs of the TS and products.

Further Investigation

Cope Rearrangement

Non-symmetric and useful Cope rearrangements could be analysed for feasibility.
Special cases of the Cope rearrangement such as hetero-Cope rearrangements exist that could be interesting.

Diels-Alder

A pair of sultine forming reactions were calculated. Other hetero-DA reactions with nitrogen and oxygen containing molecules as well as retro-DA and reverse electron demand DA reactions could be investigated.

References

↑ ^1.0 ^1.1 Mike Bearpark "Third Year Computational Chemistry Lab", 2013 Webpage
↑ Ilker Özkhan, Metin Zora, "Transition Structures, Energetics, and Secondary Kinetic Isotope Effects for Cope Rearrangements of cis-1,2-Divinylcyclobutane and cis-1,2-Divinylcyclopropane: A DFT Study", J. Org. Chem., 2003, 68 (25), pp 9635-9642 DOI:10.1021/jo035173w
↑ Eric V. Anslyn "Modern Physical Organic Chemistry", 2006, page 22
↑ Dean Markovic, Elena Roversi Dr, Rosario Scoppelliti Dr, Pierre Vogel Prof. Dr, Rubén Meana, José A. Sordo Prof. Dr., The Hetero-Diels-Alder Addition of Sulfur Dioxide: The Pseudo-Chair Conformation of a 4,5-Dialkylsultine, Chemistry - A European Journal, Volume 9, Issue 20, pages 4911-4915, October 17, 2003

[MB-1] 1.0 ^1.1 Mike Bearpark "Third Year Computational Chemistry Lab", 2013 Webpage

[Cyclooct-2] Ilker Özkhan, Metin Zora, "Transition Structures, Energetics, and Secondary Kinetic Isotope Effects for Cope Rearrangements of cis-1,2-Divinylcyclobutane and cis-1,2-Divinylcyclopropane: A DFT Study", J. Org. Chem., 2003, 68 (25), pp 9635-9642 DOI:10.1021/jo035173w

[BL-3] Eric V. Anslyn "Modern Physical Organic Chemistry", 2006, page 22

[SO2-4] Dean Markovic, Elena Roversi Dr, Rosario Scoppelliti Dr, Pierre Vogel Prof. Dr, Rubén Meana, José A. Sordo Prof. Dr., The Hetero-Diels-Alder Addition of Sulfur Dioxide: The Pseudo-Chair Conformation of a 4,5-Dialkylsultine, Chemistry - A European Journal, Volume 9, Issue 20, pages 4911-4915, October 17, 2003

[1]

[2]

[3]

[4]