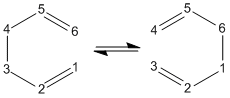Rep:Mod3jsm108

3^rd year computational: module 3

Josh McNicoll

00551754

Introduction

The following project shows the use of computational methods to find transition states in different reactions. Numerous different methods are used such as TS (Berny), the frozen co-ordinate method and QST2. A frequency analysis confirms a transition state by computing one imaginary frequency, which relates to the reaction being studied. The conformation of the product can also be predicted using computational methods via an IRC calculation.

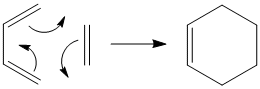
The Cope Rearrangement

The cope rearrangement is a [3,3]-sigmatropic shift rearrangement.

Optimising the reactants and products

Different conformations of 1,5-hexadiene are possible, each with a different associated energy.

Initially an anti periplanar conformer was drawn and minimised using HF/3-21G level of theory. The energy of the structure was recorded and the molecule was symmetrised to find the point group of the molecule. This method was followed for a gauche conformer. As seen the anti periplanar conformer has the lower energy when compared to the gauche conformer. This is due to the anti periplanar conformer having less steric repulsion due to the arrangement. However, the lowest energy conformer was found to be a gauche conformer (gauche 3). The low energy is probably due to favourable Van de Waals interactions between hydrogens in the molecule overriding the slightly higher steric strain. The C_i anti 2 conformer was then drawn and optimised at the HF/3-21G level of theory, and then followed by the B3LYP/6-31G* level of theory.

All of the results are summarised in the table below:

Conformation	Theory level	Computed energy (Hartrees)	Literature energy from appendix (Hartrees)	Point group	Structure	Conformer	Comments
Anti conformer	HF/3-21G	-231.6926024	-231.69260	C2	Lowest conformation structure	anti 1	The computed energy matches perfectly with the appendix energy for the conformer
Gauche conformer	HF/3-21G	-231.691667	-231.69167	C2	Lowest conformation structure	gauche 2	The computed energy matches perfectly with the appendix energy for the conformer
Lowest energy conformer	HF/3-21G	-231.6926612	-231.69266	C1	Lowest conformation structure	gauche 3	The computed energy matches perfectly with the appendix energy for the conformer
Ci anti 2 conformation	HF/3-21G	-231.6925352	-231.69254	Ci	Same as below	anti 2	The computed energy matches perfectly with the appendix energy for the conformer
Ci anti 2 conformation	B3LYP/6-31G*	-234.61170273	-234.611710	Ci	Lowest conformation structure	anti 2	The computed energy matches perfectly with the appendix energy for the conformer

The geometries for the anti 2 conformers when optimised with different levels of theory were almost identical. The geometry changes between the optimised structures can be measured by comparing the dihedral angles in the molecules. These are measured for 4 atoms, and so 3 angles can be measured along the chains; carbons 1,2,3 and 4, carbons 2,3,4 and 5, and carbons 3,4,5 and 6. Measured parameters for the HF/3-21G and B3LYP/6-31G* levels of theory are shown in the table below:

Carbons used for measurement	Low level theory HF/3-21G	High level theory B3LYP/6-31G*	Difference
1234 dihedral angle	114.626°	118.53°	3.904°
2345 dihedral angle	180.0°	180.0°	0°
3456 dihedral angle	114.626°	118.53°	3.904°
12 bond length	1.316 A	1.334 A	0.018 A
23 bond length	1.509 A	1.504 A	0.005 A
34 bond length	1.552 A	1.548 A	0.004 A

Energy difference between HF/3-21G and B3LYP/6-31G* levels for the C_i anti 2 conformation: 2.91916753 Hartrees

It can be seen that the higher level of theory gives slightly different bond lengths and dihedral angles. As seen from the table, the bond lengths are more accurate at the lower level theory than the angles. If the lower level of theory is used, bond lengths can accurately be recorded to 0.1 A, and angles to the nearest whole degree. The higher level of theory managed to locate a slightly lower energy minimum for the conformer also.

IR spectrum of the optimised anti 2 conformer at B3LYP/6-31G* level

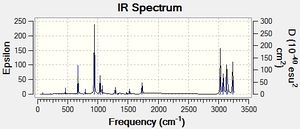
The optimized C_i anti 2 conformation B3LYP/6-31G* structure was used to run a frequency calculation at the same level of theory. All vibrations are real and positive, ranging from 73 cm^-1 to 3234 cm^-1. This result supports the idea that the optimised geometry is an energy minimum. The spectrum calculated is shown to the right.

Using the output file, the following values were found in the 'thermochemistry' section:

Sum of electronic and zero-point Energies=           -234.469212
Sum of electronic and thermal Energies=              -234.461856
Sum of electronic and thermal Enthalpies=            -234.460912
Sum of electronic and thermal Free Energies=         -234.500822

The Sum of electronic and zero-point energies= the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE).

The Sum of electronic and thermal energies= the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + E_vib + E_rot + E_trans).

The Sum of electronic and thermal enthalpies= contains an extra correction for RT (H = E + RT), which is particularly important when looking at dissociation reactions.

The Sum of electronic and thermal free energies= includes the entropic contribution to the free energy (G = H - TS)

The same values were also found for the lower basis set calculation:

Sum of electronic and zero-point Energies=           -231.539539
Sum of electronic and thermal Energies=              -231.532566
Sum of electronic and thermal Enthalpies=            -231.531622
Sum of electronic and thermal Free Energies=         -231.570909

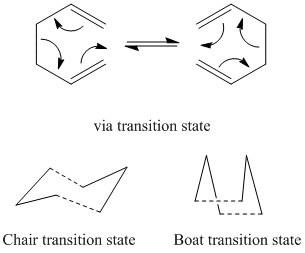
Optimizing the "Chair" and "Boat" Transition Structures

Chair

An allyl fragment (CH₂CHCH₂) was drawn and optimized using the HF/3-21G level of theory. This molecule was then pasted twice into a new window and orientated so that they look roughly like the chair transition state. The transition state was then found using 2 different methods.

Illustration of chair imaginary frequency -818 cm^-1 from optimisation to a TS (Berny)

Illustration of chair imaginary frequency -818 cm-1 from using the frozen coordinate method

The distance between the terminal ends of the allyl fragments was set to 2.2 Å. Hartree Fock and basis set 3-21G theory was used to optimise to a transition state- TS (Berny). The force constants were calculated once and opt=noeigen was added to the additional keywords (to allow an imaginary frequency to be calculated).

Imaginary frequency calculated= -818 cm^-1

The vibration was animated and seen to correspond to the Cope rearrangement.

Optimised distance between the terminal ends of the allyl fragments= 2.02045 Å

Energy of transition state= -231.61932247 Hartrees

The structure was then optimized to the transition structure using the frozen coordinate method. The fragments distances were frozen at 2.2 Å and the molecule was optimised using the opt=modredundant option. The frozen bonds were then relaxed and a transition state optimisation was set up.

Imaginary frequency calculated= -818 cm^-1

The vibration was animated and seen to correspond to the Cope rearrangement.

Optimised distance between the terminal ends of the allyl fragments= 2.02044 Å

Energy of transition state= -231.61932227 Hartrees

It can be seen that both methods have yielded the same results. The imaginary frequency is the same for both methods, and the bond lengths between the fragments are also the same to 4 decimal places, which is higher than the accuracy the lengths are normally recorded to. The transition state energies are also very similar and similar to 6 decimal places, again much higher than the accuracy the energy is normally recorded to.

Both methods are seen to be successful, but each one has a disadvantage. Luckily, the first method worked well for me here, but a good guess at the transition state is needed for the method to work successfully. The second method does not need as good a guess, but is a lot more time consuming to carry out.

Looking at the chair transition state, it is thought to connect the gauche 2 conformer, although in reality this is hard to say.

Illustration of boat imaginary frequency -840 cm^-1 from the QST2 method

Boat

The boat transition state was found using the QST2 method. The C_i anti 2 conformer was copied into a new window, and then pasted again into the same "molgroup". The reactant and product were then numbered corresponding to the reaction:

This was then sent to be optimised to a TS (QST2). The job failed and so the reactant and product were altered so that they resemble the boat transition structure. The central C-C-C-C dihedral angle was changed to 0°, whilst the central C-C-C angles were changed to 100°. The TS (QST2) optimisation was then set up again.

Imaginary frequency calculation= -840 cm^-1

The vibration was animated and seen to correspond to the Cope rearrangement.

Optimised distance between the terminal ends of the allyl fragments= 2.13940 Å

Energy of transition state= -231.60280217 Hartrees

Looking at the boat transition state, it is thought to connect the gauche 1 conformer, although again in reality this is hard to say.

IRC analysis

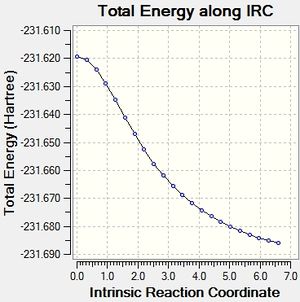
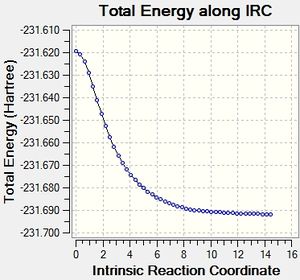
The intrinsic reaction coordinate allows you to follow the minimum energy path from a transition state down to its local minimum on a potential energy surface. Initially the calculations for the boat and chair transition states were computed with 50 steps. When the jobs had completed it could be seen that neither the boat nor the chair had managed to find a minimum. This left a couple of options left to continue with. The first method was to run an optimisation on the final structure from the initial IRC calculation. The second method was to start the IRC calculation again but with calculation of the force constants at each step. The results are shown in the tables below.

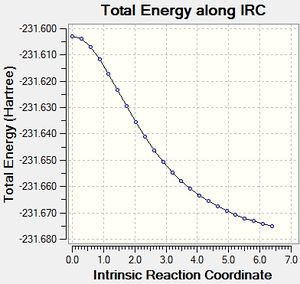
IRC chair

IRC type	Energy (a.u.)	Energy surface	Comments
Initial (50 steps)	-231.619322	Chair IRC initial	As seen from the energy graph, a minimum was not found. It can be seen that 50 steps is not high enough for a minimum to be found.
An optimisation was then run on the final structure	-231.691667	Optimisation	It can be seen that this method has accurately found a minimum energy structure.
Force constant always	-231.6916644	Chair IRC force constants always	It can be seen that this method has accurately found a minimum energy structure.

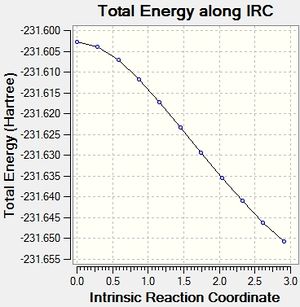
IRC boat

IRC type	Energy (a.u.)	Energy surface	Comments
Initial	-231.6750656	Boat IRC initial	As seen from the energy graph, a minimum was not found. It can be seen that 50 steps is not high enough for a minimum to be found.
An optimisation was then run on the final structure	-231.6830255	Optimisation	It can be seen that this method has accurately found a minimum energy structure.
Force constant always	-231.6506762	Boat IRC force constants always	As seen from the energy graph, this method was not successful at producing a minimum energy structure.

IRC analysis

It can be seen that the optimisation of the final structures of the initial IRCs yielded the lowest energy minima each time, and this method has been quick and effective at locating the minima for both the boat and chair transition states. Calculating the force constants at every step was successful for the chair transition state, but was not successful for the boat transition state. A minimum was found, but this was a higher energy minimum when compared to the optimisation.

The chair transition state has minimised into the gauche 2 conformation.

The boat transition state has not minimised to any of the conformers successfully. The calculation would need to be repeated initially with many more steps to be able to find the minimum, and then perhaps optimised again afterwards to be able to get a accurate minimum energy.

Obtained values and calulations

The chair and boat transition structures were reoptimized using the B3LYP/6-31G* level of theory frequency calculations were also completed. The HF/3-21G optimized structures were used as starting point. The geometries and the difference in energies between the reactants and transition states at the two levels of theory were compared, and displayed below.

Chair transition state
Property	HF/3-21G	B3LYP/6-31G*
Energy (Hartrees)	-231.6193225	-234.556983
C-C-C bond angle (°)	120.5	120
Fragments bond distance (A)	2.02	1.97
C-C bond length (A)	1.39	1.41
Imaginary frequency (cm-1)	-818	-566
Boat transition state
Property	HF/3-21G	HF/6-31G
Energy (Hartrees)	-231.6028022	-234.5430931
C-C-C bond angle (°)	121.6	122.3
Fragments bond distance (A)	2.14	2.21
C-C bond length (A)	1.38	1.39
Imaginary frequency (cm-1)	-840	-530

Looking at the results in the table, the geometries of the transitions states do not change dramatically when the level of theory is changed. However, there is quite a large difference in the energy of the transition states between the theory levels.

The activation energies were calculated for both the chair and boat transition states

Thermochemistry data has also been calculated for the chair and boat transition states and is displayed below:

Chair transition state- lower basis set

Sum of electronic and zero-point Energies=           -231.466700
Sum of electronic and thermal Energies=              -231.461340
Sum of electronic and thermal Enthalpies=            -231.460396
Sum of electronic and thermal Free Energies=         -231.495206

Boat transition state- lower basis set

Sum of electronic and zero-point Energies=           -231.450922
Sum of electronic and thermal Energies=              -231.445295
Sum of electronic and thermal Enthalpies=            -231.444350
Sum of electronic and thermal Free Energies=         -231.479112

Chair transition state- higher basis set

Sum of electronic and zero-point Energies=           -234.414929
Sum of electronic and thermal Energies=              -234.409008
Sum of electronic and thermal Enthalpies=            -234.408064
Sum of electronic and thermal Free Energies=         -234.443814

Boat transition state- higher basis set

Sum of electronic and zero-point Energies=           -234.402342
Sum of electronic and thermal Energies=              -234.396008
Sum of electronic and thermal Enthalpies=            -234.395063
Sum of electronic and thermal Free Energies=         -234.431097

Using all of the data collected, a table has been drawn showing all the energies and values calculated. The values I have calculated match very well with the values found in the reference table, and so it can be deduced that the correct strucures were successfully found.

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.6193225	-231.466700	-231.461340	-234.556983	-234.414929	-234.409008
Boat TS	-231.6028022	-231.450922	-231.445295	-234.5430931	-234.402342	-234.396008
Reactant (anti2)	-231.6925352	-231.539539	-231.532566	-234.61170273	-234.469212	-234.461856

From the data in the table above, it was possible to calculate the activation energies for the chair and the boat transition states at 0K and 298.15K. The results are shown in the table below.

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.69	34.06	33.16	33.5 ± 0.5
ΔE (Boat)	55.61	54.76	41.96	41.32	44.7 ± 2.0

It can be seen again that the values calculated match extremely well with the values given in the reference table. The values calaulcted at the higher level of theory match more closely to the literature values than the values calculated at the lower level of theory. From this approach it can be seen that using a low level of theory to map the energy surface, followed by a higher level of theory to give accurate results is a good method and efficient method.

From the data it can be seen that the chair transition state has a lower activation energy than the boat transition state, which agrees with the literature.. There is less steric hindrance when going via the chair transition state when compared to the boat transition state.

The Diels Alder Cycloaddition

The Diels-Alder reaction is a cycloaddition reaction. The reaction occurs between a diene and a dienophile, with the HOMO/LUMO from the diene interacting the the HOMO/LUMO of the dienophile. The simplest Diels-Alder reaction occurs between ethene and cis-butadiene.

Ethene and cis-butadiene

Ethene and cis-butadiene were optimised using the semi-empirical AM1 method, and the molecular orbitals were visualised. The results are shown in the table below:

Molecule	Energy of molecule	HOMO energy	HOMO image	HOMO symmetry (with respect to σv plane)	LUMO energy	LUMO image	LUMO symmetry (with respect to σv plane)
Ethene	0.02619028	-0.38775	Ethene HOMO	Symmetric	0.05283	Ethene LUMO	Antisymmetric
Cis-butadiene	0.04879738	-0.3438	Cis butadiene HOMO	Antisymmetric	0.01707	Cis butadiene LUMO	Symmetric

It is known that only orbitals of the same symmetry can interact, and so it can be seen that the LUMO of ethene can interact with the HOMO of cis-butadiene, and the HOMO or ethene can interact with the LUMO of cis-butadiene.

Diels-Alder reaction

The transition state for the reaction was calculated. A bicyclic system was first drawn and optimised. The CH₂-CH₂ fragment was then removed. The fragment end distances were first guessed at 2.15 A and the molecule was optimised to a TS (Berny).

This yielded a good result, with one imaginary frequency at -818 cm^-1. The vibration matched with the Diels-Alder reaction. It can be seen that the bond formation is synchronous, agreeing with the fact that the Diels-Alder reaction has concerted bond forming.

The lowest real frequency is observed at 167 cm^-1. This is seen to be a rocking of the "ethene" part of the transition state.

Transition state energy= -231.60320855 Hartrees

Imaginary vibration at -818 cm^-1 relating to the Diels-Alder reaction

HOMO

LUMO

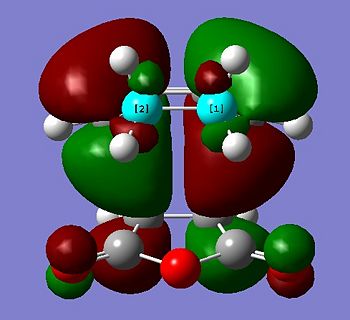
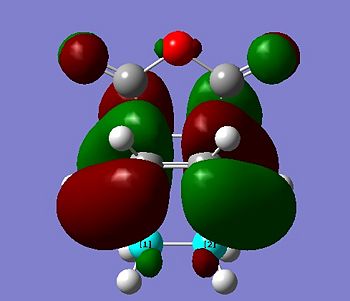
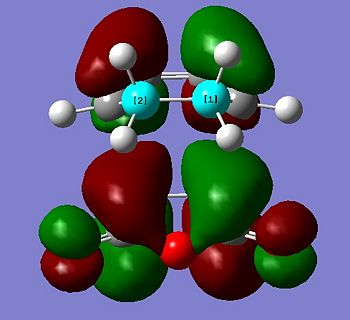
The transition state HOMO is observed to be antisymmetric in symmetry. It can be deduced that the HOMO has been formed from the interaction between the LUMO of ethene and the HOMO of cis-butadiene because they are both antisymmetric. The transition state LUMO is observed to be symmetric, and so has been formed from the interaction between the HOMO of ethene and the LUMO of cis-butadiene because they are both symmetric.

Some measured parameters for the reactants and the transition state have been summarised in the table below.

Measurement	Reactants	Transition state
Fragment C-C bond length	-	2.21 A
Ethene C=C bond length	1.33 A	1.38 A
Butadiene C=C bond length	1.34 A	1.37 A
Butadiene C-C bond length	1.45 A	1.39 A
Butadiene C-C=C angle	125.6°	121.5°

It can be seen that the values seen above match well with predictions about what would happen to the bond lengths and angles going from the reactants to the products. The fragment bond length is a lot longer than any of the other C-C bonds. This is the case because these bonds are only part formed. All the C-C bonds have more or less become equal in the transition state. This matches well with the electron movement in the mechanism shown above for the reaction. The butadiene angle has also decreased going from the reactant to the transition state, and has moved closer to 120°, which would be my prediction for the bond angle within the hexene product.

Typical sp³ C-C bond lengths have been found to be 1.54A and typical sp² C-C bondlengths have been found to be 1.34A.

The van der Waals radius of the C atom has been found to be 1.7 A.

The values for aveage C-C bond lengths match well with the bond lengths measured in the reactants, as expected. The transition state bond lengths sit between the values, as expected as well, because they would be inbetween sp² and sp³ bonds.

The van der Waals radius is larger that the bond lengths in the molecule, but smaller than the bond length for the fragments C-C bond distances (part formed bonds). This was the expected result.

The reaction between cyclohexa-1,3-diene and maleic anhydride

Cyclohexa-1,3-diene and maleic anhydride react in a Diels-Alder reaction to give primarily the endo product. The reaction is supposed to be kinetically controlled so that the exo transition state should be at a higher energy. The reaction scheme is shown below:

Transition state calculations

Bicyclo systems were built and optimised. The -CH2-CH2- fragments were then removed depending on which transition state was wanted. The interfragment distances were guessed at 2.2 A the strcutres were optimised to a TS (Berny) to characterise the transition structures. The transition structures were confirmed by running a frequency analysis and looking for one imaginary frequency that related to the reaction in focus. Bond lengths and distances along with the HOMOs and LUMOs were also calculated and recorded. All the information is displayed in the table below.

Property	Exo	Endo
Product energy (Hartrees)	-0.15990927	-0.16017083
Transition state energy (Hartrees)	-0.05041985	-0.0515048
Imaginary frequency vibration cm<sup>-1</sup>	-812	-806
Imaginary frequency vibration animation	Exo vibration	Endo vibration
Lowest real frequency cm<sup>-1</sup>	61	62
Lowest real frequency description	Rocking of cyclohexadiene fragment	Rocking of cyclohexadiene fragment
Fragment bond distance	2.17	2.16
(C=O)-C-(C=O) through space distance	2.27963	2.27923
C=C distance	1.39676	1.39724
C-C bridge distance	1.52208	1.52297
HOMO (highlighted carbons are the bridging CH2-CH2 carbons)	Exo HOMO Antisymmetric	Endo HOMO Antisymmetric
LUMO (highlighted carbons are the bridging CH2-CH2 carbons)	Exo LUMO Antisymmetric	Endo LUMO Antisymmetric

The biggest result that agrees with the endo product being favoured is the transition state energy and the product energy. The endo product has a lower transition state energy than the exo transition state energy, and also a product energy lower than the exo product energy.

The fact that the endo transition state has a lower energy means that, if the reaction is under kinetic control, the endo product will favour as it has a lower kinetic barrier than the exo product.

The endo fragment has slightly shorter fragment bond distances when compared to the exo product, meaning the fragments are slightly closer together. This is a logical observation as this agrees with the above result.

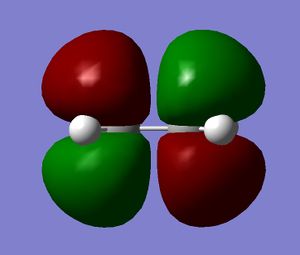
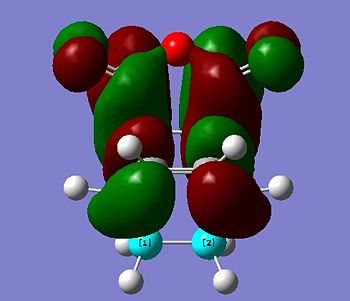
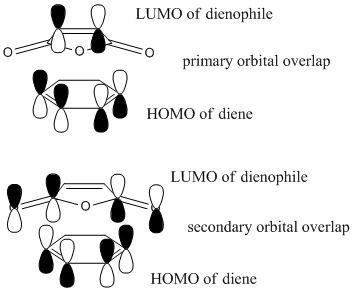
Looking at the HOMOs for both transition structures, there is a difference in the (C=O)-O-(C=O) region of the products. The exo product has no visible electron density in this region, whereas the endo product has visible electron density in this region. From this, it can be concluded that there is significant secondary orbital overlap in the endo product when compared to the exo product. The secondary orbital overlap in the endo transition structure will stabilise the transition state and cause a lowering in the energy. This stabilisation is not seen for the exo transition state. A diagram summarising this interaction is shown below:

Conclusion

It can be seen that computational calculations are extremely useful. It is possible to accurately predict the transition state of a reaction via numerous methods, as well as to trace the energy surface to find which conformer will be formed from the found transition state. A range of different values such as the activation energy can also be calculated for transition states, allowing us to differentitate between high and low energy transition state pathways. Molecular orbital calculations of the reactants and transition states give a good picture about the orbital interactions that have occured to form the molecular orbitals of the transition state.

In the Diels-Alder transition state calculations there a numerous things that have been negelected. For example, the role of solvents in the reaction could be quite large, and vary the transition states and their energies to some extent. This would change the nature of the reaction and the leading product, depending on the solvent the reaction is carried out in. If I had more time, I would investigate this further to see the extent of effect solvent has on the reaction.