Rep:Mod3ejc107
Module 3
The Cope Rearrangement
The purpose of this module is the characterisation of the possible transition states located on the potential energy surface in the cope rearrangement:
The calculations will involve MO methods and numerical solutions to the schrodinger as opposed to molecular mechanics methods which do not allow for the breaking and formation of bonds.
The calculations are based on gradient anaylsis of steps taken along the reaction potential energy curve.
At a transition state a maximum in the potential energy surface will be observed and as of such a first derivative = 0. The second derivative is also important and will give a negative value. This is reflected in the vibrational frequencies and therefore a negative vibration.
The optimisation of reactants is to a minima on the potential energy surface, with all positive vibrational frequencies.
Reactant Optimisation
The first step in the location of the transition state is the calculation of the reactant geometry.
The reactant 1,5-hexadiene can be considered to be in a gauche or antiperplaner arrangement based on rotation around the central C-C bond.
Rotations around the other C-C bonds leads to differing anti and gauche structures:
a)
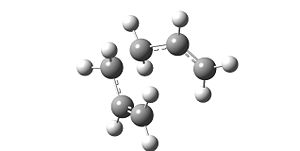
The first guess at a reactant was to try an antiperplaner structure and optimise it using a very simple Hartree-Fock method and the simple 3-21g(d) basis set.
Optimisation using Gaussian resulted in the following structure:
The energy recorded was = -231.69260 Hartrees which can be converted to -145389.19kcal/mol
1 Hartree = 627.509kcal/mol
The point group was noted as C2 and can be identified as anti-1 from the lab appendix
b)
The next step was to optimise a gauche structure using the same basis set and method, so that relative energies can be directly comparable.
The initial gauche conformer formed is shown below:
The energy obtained from this calculation was: -231.69266 Hartrees
This correlates to an energy of -145389.23kcal/mol which can be seen to be of lower energy than the optimised anti conformer.
The point group was noted C1 and the conformation confirmed as Gauche 3 from the lab appendix
c)
From the above optimisations the gauche conformation seems to be favoured slightly.
The next step was then to try various gauche conformations and see the optimised energies
The result of this is that gauche 3 orginally calculated is the lowest in energy and the most stable, this is most likely due to steric interactions.
d-e)
The anti 2 structure was optimised by the Hartree-Fock method with the 3-21g basis set
This resulted in:
An energy of -231.69253 Hartrees / -145389.15kcal/mol was obtained aond point grup of Ci
f)
The anti 2 structure was re-optimised with a higher level basis set (6-31g(d)) to obtain a more accurate reactant geometry:
The energy was reported to be -234.61171 Hartrees, -147220.96 kcal/mol however this is not directly comparable to previously quoted energies as you should not directly compare energies from different basis sets.
The point group like before is reported as Ci however the major difference in the structures is the angle of the central carbons, 112.67o compared to 111.35o:
g)
The final step in the optimisation of the reactants is a frequency calculation, which allows both a conformation that the minima has been obtained (see earlier) and gives values that are realistically comparable to one's experimentally obtained.
The frequency calculation was carried out on the 6-31g(d) optimised structure using the same basis set.
The job return all positive and real vibrations, selected relevant stretches are shown below along with an IR spectrum:
| Wavenumber | Infrared | Vibration Image |
|---|---|---|
| 940.41 | 55.31 | 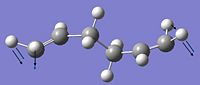
|
| 3031.61 | 53.60 | 
|
| 3137.15 | 56.07 | 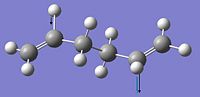
|
| 3233.93 | 45.49 | 
|
IR Spectrum
The output file from the vibrations listed the relevant thermochemical information shown below:
This gives an energy at 0K of -234.46918 Hartrees, -147131.52 kcal/mol and a thermal correction for 298.15K as -234.46184 Hartress, 147126.92 kcal/mol
Transition States
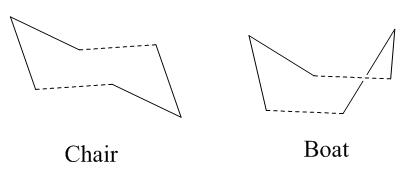
The Cope rearrangement is generally considered to go either by a chair or boat transition state:
The transition states for both the chair and boat can be considered to be constructed from 2 C3H5 allyl fragments
Chair Transition State
The chair transition state was modelled using two different methods but both centred around a predicted transition state from the combination of the two allyl fragments:
Note: The distance between the fragments was estimated at 2.2A
The first method for optimisation of the chair transition state involves an initial calculation of a force constant matrix (Hessian) that is updated during the optimisation.
Hartree-Fock method with a 3-21g basis set was used for an optimisation and frequency calculation to a ts(berny). The force constants were set to only be calculated once rather than in every step and the calculation was set to incorporate the possibility of more than one imaginary frequency.
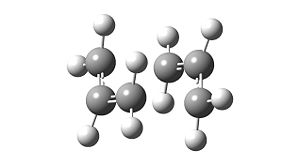
The resultant structure is shown below:
The transition state is highly similar to the predicted transition state however the distance between the two allyl fragments has been reduced to 2.02A
The frequency showed one imaginary solution at 818cm-1, which can be seen to be relate to the bond forming in the cope rearrangement
The second method involves fixing the reaction coordinate for the important bond forming places and optimising the rest of the structure. The reaction coordinate then can be optimised to a transition state with less hessian calculations and potentially time saving.
The restriction was made so that the two allyl fragments were 2.2A apart using the redundant coordinate editor. The optimisation to a minimum and then to a ts(berny) used a Hartree-Fock method with 3-21g basis set.
The results are shown below:
The same result as before was obtained with a inter-allyl distance of 2.02A. This is expected as both methods are optimising to the same transition state and the initial guess is quite close.
Boat Transition State
The boat transition state was calculated using the QST2 method, which is based on providing the reactant and product geometries and allowing Gaussian to go back and forth to indentify the transition state.
The reactants and products selected were based on the anti 2 structure. The first trial was to use them just as they had been optimised.
This job failed to converge on the desired transition state, so clearly the reactant and product molecules were not close enough to the transitions state for Gaussian to recognise the reaction procedure.
The reactant and product geometries were then therefore improved to closer match the transition structure by modifying the dihedral from 180oto 0o and central carbon angles from 111o to 100o:
This QST2 calculation gave the following transition state:
This seems to represent the boat structure and suggests the optimisation had correctly converged
Intrinsic Reaction Coordinate
From the transition structures alone it is hard to determine the conformer the transition state will result in, however this can be calculated using the intrinsic reaction coordinate method.
The method takes a set number (50 was chosen) of steps down the steepest potential energy gradient. The force constants were chosen to be calculated only once.
This resulted in a structure that hadn't properly converged:
The convergence was achieved by recalculating the IRC with force constants at every point. This is more computationally heavy than optimising the currently obtained structure to a minimum however considered more reliable. Giving the calculation more points is also likly to be less helpful as the calculation stopped after 27 steps anyway.
The IRC involved 47 steps and the revealed the gauche 2 conformer resulting from the transition state. The conformer is best seen in the penultimate step.
The point group of the IRC product is noted as C2
Activation energies
Activation energies defined as the distance between the reactants and the transition state can be calculated for the 3-21G basis set. The reactant used is the anti 2 conformer recorded earlier.
| Structure | Electronic Energy | Sum of electronic and zero-point energies (a.u.) (0K) | Sum of electronic and thermal energies (a.u.) (298.15K) | Activation Energy (a.u.) 0K | Activation Energy (a.u.) 298.15K | Activation Energy (kcal/mol) 0K | Activation Energy (kcal/mo) 298.15K |
|---|---|---|---|---|---|---|---|
| Chair | -231.61932 | -231.46670 | -231.46134 | 0.07284 | 0.07123 | 45.71 | 44.69 |
| Boat | -231.60280 | -231.45093 | -231.44530 | 0.08866 | 0.08727 | 55.61 | 54.76 |
| Anti 2 | -231.69254 | -231.53954 | -231.53257 |
This however could be more accurately reported using the 6-31g(d) higher level basis set after the calculated transition states were reoptimised.
| Structure | Electronic Energy | Sum of electronic and zero-point energies (a.u.) (0K) | Sum of electronic and thermal energies (a.u.) (298.15K) | Activation Energy (a.u.) 0K | Activation Energy (a.u.) 298.15K | Activation Energy (kcal/mol) 0K | Activation Energy (kcal/mo) 298.15K |
|---|---|---|---|---|---|---|---|
| Chair | -234.55698 | -234.41493 | -234.40901 | 0.04988 | 0.05283 | 31.30 | 33.15 |
| Boat | -234.54309 | -234.40234 | -234.39601 | 0.06684 | 0.06583 | 41.94 | 41.31 |
| Anti 2 | -234.61172 | -234.46918 | -234.46184 |
The Transition States for the 6-31g(d):
| Chair | Boat |
|---|---|
 |
File:Ejc107boatts631.jpg |
| DOI:10042/to-4800 | DOI:10042/to-4802 |
The activation energies at 0K compared to experiment can be summarised as below:
| TS | Activation 3-21g (kcal/mol) | Activation 6-31g(d) (kcal/mol) | Experiment[1] |
|---|---|---|---|
| Chair | 45.71 | 31.30 | 33.5 ± 0.5 |
| Boat | 55.61 | 41.94 | 44.7 ± 2.0 |
It is clear that the chair transition state is lower in activation energy and therefore expected to be the dominant process. The comparisons were made with anti 2 however gauche 2, which the transition state resulted in or gauche 3, the lowest energy conformer might have been more appropriate
The geometries from the 6-31g(d) optimisation are very similar however there are significant difference's in the energies. There is far closer correlation to the literature sources in the 6-31g(d), this is due to the higher accuracy of both the B3LYP method and the higher 6-31g(d) basis set.
It is important to note is that while direct comparison between two absolute energy values from two different basis sets is nonsense, energy difference's such as activation energies are allowed to be compared.