Rep:Mod3db2409wd6
3rd year computational project
Introduction
throughout this report transition states for various pericyclic reactions are identified and positioned between the reactant and products on the potential energy surface. Various computational methods will be used an evaluated by comparison with literature.
- The first part will explore the Cope rearrangement as a simplified learning exercise as both the reactants and products are identical. The chair and boat transition states will be optimised using different computational techniques. The optimised chair and boat transitions will then be compared and the mechanism elucidated. A temperature study will also be conducted to monitor the change in energy with temperature
- The second part will explore the Diels Alder reaction between butadiene and ethylene computationally. The calculations will compare the accurate DFT B3LYP/6-31G* method with the less accurate AM1 method. In addition, frequency, MO and IRC analysis will be used to elucidate the reaction pathway and mechanism.
- The third part will explore the regioselectivity of a more complicated Diels alder reaction between Maleic anhydride and Cyclohexadiene. This section will once again try to evaluate the reliability and accuracy of the DFT and AM1 method for a more complex Diels alder reaction. Frequency, MO and IRC calculations will also be used once again to elucidate the reaction pathway and mechanism.
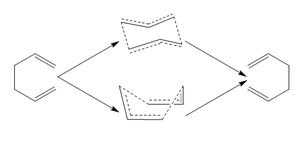
Cope Rearangement
Aims: Locate the low energy minima and transition structures on the C6H10 potential energy surface, in order to determine the preferred reaction mechanism. In addition, a range of energy values extracted from the thermochemsitry output file will be compared to literature and used to evaluate the reliability and accuracy of the computational methods.
Introduction:
For the first part of the report computational techniques will used to analyze the transition states involved in the [3,3] Cope rearrangement of 1,5 hexadiene. It has been well documented that the reaction occurs in a concerted fashion via an aromatic loose-chair transition state or the higher energy boat transition[1]. We would expect the transition state to be similar to cyclohexane and thus we would expect either the boat of chair conformations. The B3LYP/6-31G(d) method has been shown to give activation energies and enthalpies that are in good agreement with experimental values. The energies of the transition states with respect to reactants will elucidate the kinetics of the reaction. As the difference in energy between the reactants and the TS corresponds to the activation energy of the reaction.
Optimisation
Experimental
In order to calculate the lowest energy conformation we must first analysis the structures which are lowest in energy. Thus, graph below displays the relative energies of the different conformations of butadiene [2]. The graph clearly identifies the antiperiplaner conformation as being the most stable.

The antiperiplaner 1,5 hexadiene was drawn on Gaussview 5. The structure was then cleaned and optimised using HF/3-21g method as low level optimisation. The gauche conformation was then drawn on Gaussview 5. The structure was then cleaned and optimised with the low level HF/3-21g method again. The memory used in the calculations were changed to 250Mb to prevent severe error #2070. The symmetry point groups and energy values for the 4 anti conformations and the 6 gauche conformations were extracted from checkpoint files. The tabulated values can be seen below and from this we can identify the most stable anti and gauche conformations.
| Conformation | 3D jmol link | Total energy (Ha) | Point group | relative energy (kcal/mol) |
|---|---|---|---|---|
| Anti 1 [3] | Click Here | -231.69260 | C2 | 0.04 |
| Anti 2 | Click Here | -231.69254 | Ci | 0.08 |
| Anti 3 | Click Here | -231.68907 | C2h | 2.25 |
| Anti 4 | Click Here | -231.69097 | C1 | 1.06 |
| Gauche 1 | Click Here | -231.68772 | C2 | 3.10 |
| Gauche 2 | Click Here | -231.69167 | C2 | 0.62 |
| Gauche 3 | Click Here | -231.69266 | C1 | 0.00 |
| Gauche 4 | Click Here | -231.69153 | C2 | 0.71 |
| Gauche 5 | Click Here | -231.68962 | C1 | 1.91 |
| Gauche 6 | Click Here | -231.68916 | C1 | 2.20 |
It is clear form the above table it is clear that the lowest 3 energy conformer are the gauche 3 and the anti 1 and 2 conformers. However the graph suggests that the antiperiplaner conformer is in fact the lowest energy conformer. We would also expect much better orbital overlap for the antiperiplaner conformer. Literature states that the Gauche conformation is 3Kjmol-1 higher in energy than the antiperplaner conformation. [4]. Thus, these three lowest energy conformers were then re-optimised using the higher level DFT B3LYP/6-31G* Opt-Freq method. At this level the lowest energy structure is the anti 2 conformation with a very small energy difference between the two. The gauche conformer is clearly less favorable now, perhaps the п-п Molecular orbital interaction helps stabilize the molecule

An important observation was that the DFT method resulted in tighter but very similar structures. They provided a means of obtaining a tidier version of the same structure. This supports the reliability of using a low level calculation to map an approximate potential energy surface but not for comparison of calculated parameters to literature. The differences between the two optimized structure of the Anti 2 conformation can be seen below.
| Table 2 HF/3-21g | DFT B3LYP/6-31g* |
|---|---|
| Click Here | Click Here |
| Conformation | Energy (Eh) | relative values (kcal/mol) |
|---|---|---|
| Anti 1 [5] | -234.61179 | |
| Anti 2 [6] | -234.61172 | |
| Gauche 3 [7] | -234.6113 |
Frequency analysis
A frequency analysis was carried out on the lowest three conformations, in order to determine whether the true minimum had been found. The three spectra obtained were almost exactly the same and all displayed the expected vibrational modes for a linear diene. The spectra for only the Anti1 conformer can seen below.
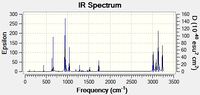
The most important vibrations was that associated with the C=C moiety. The peak is expected to be found between 1680 and 1620cm-1[8]. The table below tabulates these vibrations for anti and gauche conformers. It is clear that each conformer displays a symmetric and a asymmetric vibrational mode, with the asymmetric mode being found at higher wave numbers.
| Conformation | Animation | Description of Vibration | Frequency of vibration | intensity of vibration |
|---|---|---|---|---|
| Anti 1 [9] | Animate | Symmetric C=C stretch | 1731.96 | 4.7 |
| Anti 1 | Animate | Asymmetric C=C stretch | 1734.86 | 13.6 |
| Anti 2 [10] | Animate | Symmetric C=C stretch | 1731.46 | 0 |
| Anti 2 | Animate | Asymmetric C=C stretch | 1734.67 | 18.1 |
| Gauche 3 [11] | Animate | Symmetric C=C stretch | 1731.86 | 6.9 |
| Guache 3 | Animate | Asymmetric C=C stretch | 1732.98 | 6.1 |
The fact that no negative frequencies were obtained suggests that the produced optimized structures are in fact global minima. The peak values obtained were not identical to literature but are within acceptable error limits. For the gauche conformation the degree to which the C=C bonds stretch is very different. For the symmetric stretch, one alkene stretch is off a much greater amplitude than the other alkene moiety. The same phenomenon is observed for the asymmetric stretch . One explanation could be due to the lack of symmetry in the C1 Gauche molecule. Nevertheless, the peaks are found in very similar positions to those of the Anti conformers and the gauche vibrations are animated in the table above. Thus, the frequency analysis has been a powerful tool for making accurate IR predictions and evaluating the optimisation success. The following section will extract even more detailed information from the frequency analysis
Thermochemical data for the reactant and products
By looking at the output file from the frequency analysis we can extract the thermochemical data relating to each conformer. The four important values for each isomer are defined and displayed below.
1) The first value is the overall potential energy at 0K, including the zero point vibrational energy
2) The second value correspond to the overall potential energy at 298.15K and 1 atmosphere. This value includes contributions form the vibrational, translational and rotational modes (E=E+Evib+Etrans+Erot)
3) The third value is the correctional term for RT, this proves to be extremely important when evaluating the dissociation reaction (H=E+RT)
4) The fourth value incorporates the entropic contribution to the free energy (G=H-TS)
| Conformer | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and thermal free energies |
|---|---|---|---|---|
| Anti 1 [12] | -234.469298 | -234.461966 | -234.461022 | -234.500862 |
| Anti 2 [13] | -234.469186 | -234.461849 | -234.460904 | -234.500735 |
| Gauche 3 [14] | -234.468693 | -234.461464 | -234.460520 | -234.500105 |
Furthermore, by modifying the input file we can run the frequency analysis at different temperatures and pressures. Thus, the input files were modified setting the temperature to 0.0001K and 1.0 atmospheres. The values that were obtained at 0K from the output all converged to a single value as there are no thermal contributions for each conformer. The table below displays the converged value for all four thermochemical properties
| Conformer | converged value (Ha) |
|---|---|
| Anti 1 [15] | -234.468861 |
| Anti 2 [16] | -234.468749 |
| Gauche 3 [17] | -234.468256 |
At OK only the zero point energy is accounted for. If additional time were available a variety of temperatures and pressures could be tested. This would allows us to elucidate the extent of which these parameters are affected by a change in temperature and pressure and how they affect the total energy of the system. Nevertheless, we would expect that as the temperature increases the second and third values will increase. The reason for this is because at higher temperatures, there are greater thermal contributions to the both the energy and enthalpy of the system. We would expect the fourth value to decrease as the temperature is raised. This can be rationalized through the Gibbs free equation (G=H-TS). We can clearly see that as the temperature increases the TS terms becomes more negative and as a result the free energy will decrease.
Optimising Transition States
Chair optimisation
Now that we have mapped the potential energy surface by pin pointing the minima, the transition states for the reaction can be identified. The approximation that the TS structure exists as either a boat or chair conformation is a good starting hypothesis. However, in order to accurately assign the transition state its position on the potential energy surface must link the reactants and the products. Numerous approaches were used and will be evaluated in this section of the report.
The first transition state that was analyzed was the chair conformation. This was done by drawing the allyl fragment which was optimised with the basic HF/3-21G level. The optimised allyl group was then duplicated and pasted twice into a new window. The two fragments were then positioned in the chair conformation with the corresponding terminal carbon atoms moved to distances around 2.20A. From here there are two optimisation methods that will be outlined.
1) This first method involves computing the force constant matrix and updating it as the optimization proceeds. This method allows us to accurately approximate the transition state structure with reasonable accuracy. However, one of the major limitations to this method is the presence of local minima near the approximated structure perturbing its true structure. Nevertheless, as we are dealing with a relatively simple well defined transition state, we would expect to obtain relatively accurate results. The HF optimised allyl fragments were manipulated to the guess chair transition structure. This was then optimised using the following key words
opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity
The above line tells Gaussian to calculate force constant once, to minimise the structure to a Berny transition state. The NoEigen prevents the program from terminating if more than one imaginary frequencies are obtained. This structure was run under the Opt+freq method using the HF/3-21G calculation.

The optimisation leads to the structure shown on the right with an imaginary frequency at -817cm-1. The animation of this frequency shows the expected Cope rearrangement and proves that a transition state structure has been found. The distance between the terminal carbons was found to be 2.03A.
2) The second method essentially freezes the reaction coordinate and minimizes all other degrees of freedom. This is thought to be useful for bypassing force constant calculations as this method allows a reasonable guess of the force constant matrix. This method also filters out other possible imaginary frequencies that should not be found in the transition state. This method involves a two step optimisation. The initial optimisation involved freezing the bonds between two terminal carbon bonds on the Redundant coordinate editor. The terminal distances were set to 2.20A. The rest of structure was then optimised using HF method. The frozen coordinate is then removed from the output file and set to the derivative option. The opt+freq method to TS (Berny) using the HF calculation was then run. Producing the same transition structure with an imaginary frequency at -818.04cm-1 which agrees the imaginary frequency that was calculated for the first method.
Boat optimisation
The previous method revolved around finding the maximum point on the PES by obtaining a negative frequency which indicated that the second derivative was a maximum. This method attempts to interpolate between the minima of the reactant and products and approximate the transition state. The fact that the reactants and products are identical suggests that there should be two symmetric minima about the transition state. Thus for this method the reactant will be duplicated in order to serve as a representation of the product.

In order to obtain a successful calculation the atomic labels had to be changed in order to allow the reactant to map onto the product. This was done on the atom list on Gaussview. The reactant and product were labelled as shown below.
| Reactant | product |
|---|---|
 |
 |
Once the reactant and product had been labelled correctly an Opt+freq calculation was run using the TS(QST2) method calculated the force constant matrix once. However, this calculation immediately failed because the calculation could not account for rotation around the C-C bonds. Thus, the reactant and product molecules had to be modified further by changing the dihedral angle for the four central Carbons (C2-C3-C4-C5) to 0o and the inner bond angle (C2-C3-C4 and C3-C4-C5) were set to 100o. This produced the structures shown below
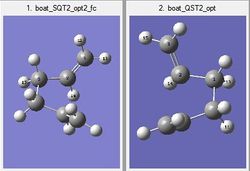
The calculation was successful and modeled the transition state well. The presence of one imaginary vibration at 839.97cm-1 confirmed a successful calculation. This frequency corresponds to the global maximum of the transition state. For the boat transition state the distance between the terminal carbon atoms was found to be 2.14A. The imaginary vibration representing the Cope reaction coordinate can be seen below
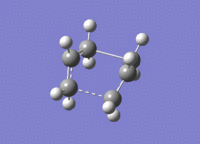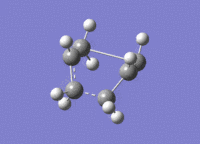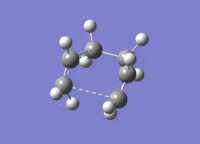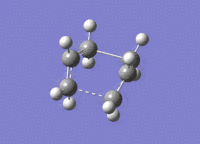
| Transition state | 3D jmol link | Method | Bond Length between Terminal Carbons (A) |
|---|---|---|---|
| Allyl Fragment | Click Here | HF/3-21G Optimisation | - |
| Chair [19] | Click Here | Optimisation to a Berny TS | 2.02 |
| Chair [20] | Click Here | 1st Frozen Coordinate | 2.20 |
| Chair [21] | Click Here | 2nd Frozen Coordinate | 2.02 |
| Boat [22] | Click Here | TS(QST2) | 2.14 |
Conclusion
Throughout this part of the report various computational techniques have been employed in order to evaluate their accuracy. Thus, the DFT-B3LYP/6-31G* in terms of geometry optimization has been the more reliable method than the primitive HF/3-21G. The more sophisticated DFT method provided optimized geometries that agreed with theory and was able to calculate thermochemical data to higher degree of accuracy, which can be seen in the activation energies previously calculated.
Furthermore, the fact that the imaginary vibrations support the formation of the transition state, suggests that they were successfully modeled using the Opt+Freq job type. In addition, despite the frozen coordinate method being run in two steps it proved to be the more effective and faster method for optimising the chair transition state. The reason for this was due to fact that we could define the expected transition state better than the force constant method, by freezing the forming bonds and allowing the rest of transition to relax. The QST2 method proved effective for the boat transition state but was much more time consuming as the reactant and products had to be manually labelled. Thus, this method would be ineffective when dealing with larger molecular systems.
The IRC calculations proved to be an effective means of monitoring how the trnasition state tends towards a local energy minimum. This method was explored further by having the force constant calculated always. However, this did result in much longer calculations. Finally, these techniques that have been used so far will be used to model the Diels Alder Transition states.
Intrinsic Reaction Coordinate analysis
It is virtually impossible to accurately predict the product that the transition state will form. Thus, the intrinsic reaction coordinate method allows us to follow the minimum energy path on a PES from a transition state to a local minimum structure. The final structure can then be analyzed to elucidate the transition state it is most similar to. The IRC method was selected for the chair conformation in the forward direction as the reaction coordinate is symmetrical. In addition, the force constant was calculated once and the maximum number of steps was set to 50. The figures below displays the variation of the total energy and the RMS gradient at each step along the minimum energy pathway. An image of the of the final structure (after 24 steps) can be seen below.
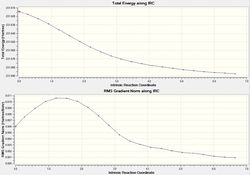
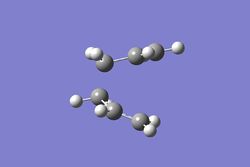
The calculation terminated after 21 steps with the final structure not exhibiting a bond between the two of the terminal Carbons. As an overall energy minimum has not yet been reached one of three methods outlined below can bow be taken.
1) Perform an energy minimisation on the final step structure. This is fastest of the three methods but will be unsuccessful if the final structure is far away from the local minimum
2) Perform the IRC calculation again but increase the maximum number of steps. This method is fairly reliable but if the maximum step limit is too high then we might obtain a structure that is very different from what we would expect.
3) Perform the IRC calculation again but specify that the force constant is computed "always". This method is by far the most reliable but requires much more computing time, especially for larger molecules.
Method 1 was carried out first and the final structure was optimised using the HF/3-21G method. The total energy was found to be -231.69167, which is exactly the same as the value obtained for the Gauche 2 conformation calculated previously. This suggests that the Gauche 2 structure is the most likely conformation to be formed after the transition state. Method 2 was then carried out raising the maximum step limit to 100 steps. This resulted in the same results previously obtained as the calculation terminated after 22 steps. Furthermore, method 3 produced the same Gauche 2 conformation after 47 steps, which can be seen below. The overall summary of the IRC calculations can also be seen below

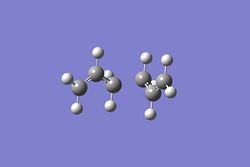
| Name of Transition state | Maximum number of steps | Compute Force Constant | Terminated After | Total Energy (a.u) |
|---|---|---|---|---|
| Chair [23] | 50 | Once | 22 steps | -231.614 |
| Chair [24] | 100 | Once | 22steps | -231.614 |
| Chair [25] | 50 | Always | 47 steps | -231.6917 |
| Boat [26] | 50 | Always | 61 steps | -231.6028 |
Activation Energies For the Chair and Boat Transition structures
The final part of this section subjects the transitions state structures to the more accurate DFT-B3LYP/6-31* method. This allows us to elucidate and evaluate the difference between the optimisation methods.
Thus, the activation energy of the reaction was calculated for each transition state under both the DFT and HF methods. The activation energy is defined as the amount of energy required for the reactants to form the transition states. For the HF/3-21G method the transition state was compared to Gauche 3 conformation, as this was the lowest energy conformer under this basic method. For the DFT method the transition state was compared to the anti 1 conformation, as this was the lowest energy conformer under this more advanced method. Thus, the energy difference was calculated by subtracting the two energy values in Hartrees and then multiplying this difference by 627.5 to convert it into kcal mol-1. The table below tabulated the main parameters and the point groups were calculated using the Edit-Symmetrize function on Gauss-view.
| Transition State | Symmetry | HF Energy of TS | HF Energy of Gauche 3 | HF Activation Energy (kcalmol-1 | DFT Energy of TS | DFT Energy of Anti 1 | DFT Activation Energy | Literature Activation Energy [27] (kcalmol-1) |
|---|---|---|---|---|---|---|---|---|
| Chair [28][29] | C2h | -231.61932 | -231.69266 | 46.02 | -234.55698 | -234.61179 | 34.39 | 33.5±0.5 |
| Boat [30][31] | C2v | -231.60280 | -231.69266 | 56.39 | -234.49291 | -234.61179 | 74.60 | 44.7±2.0 |
In addition, the activation energy was calculated at 0.0001K. This calculation involved taking the difference between the electronic and zero point energy value and the electronic and thermal energy value. This energy is the additional energy required to activate the reaction at 0.0001K. Thus, the activation energy at 0K was found by adding this difference to the activation energy at 298.15K.
| Transition State | HF/3-21G Method electronic and Zero Point Energy | HF/3-21G Method Electronic and Thermal Energy | HF Activation Energy (kcalmol-1) at 298.15K | Activation energy (kcalmol-1) at 0.00K | DFT-B3LYP-6-31* Method - Electronic and zero point energy | DFT-B3LYP/6-31* Method- Electronic and thermal energy | Activation Energy(kcalmol-1) at 298.15K | Activation energy (kcalmol-1) at 0.00K | Literature Activation Energy[32] (kcalmol-1) |
|---|---|---|---|---|---|---|---|---|---|
| Chair [33][34] | -231.466690 | -231.461331 | 46.02 | 49.38 | -234.414932 | -234.409010 | 34.39 | 38.10 | 33.5±0.5 |
| Boat [35][36] | -231.450928 | -231.445299 | 56.39 | 59.92 | -234.351313 | -234.345015 | 74.60 | 78.55 | 44.7±2.0 |
It is clear from the above table that the DFT method provides more accurate results as the activation energy for the chair TS is extremely close to literature. However, the boat transition state has a much larger activation barrier than that reported in literature. This could be due to a number of reasons and may suggest the presence of an anomalous energy value for the DFT optimized boat conformation, resulting a much greater difference with the Anti 1 conformer. Overall, the DFT method is more suitable and accurate for calculating activation energy values.
Diels Alder
For this part of the report, the techniques previously outlined will be used to model and analyze the transition states associated with two Diels alder reactions. The first reaction that will be explored is the relatively simple reaction between ethane and cis-butadiene. The endo and exo selectivity will then be investigated through the Diels alder reaction between cyclohexadiene and maleic anhydride. A semi empirical AM1 method will be employed to optimise the geometries and model the transition states. Furthermore, Molecular orbital analysis will be used to visualize the HOMO and the LUMO of the reactant and transition states.
Introduction
It is generally well documented that a diels alder reaction is a specific pericyclic reaction falling under cycloaddition. For the reaction to be a diels alder reaction it must proceed via a [4s+2s] cycloaddition. The reaction involves the π orbitals of diene (e rich) forming two new σ bonds with the π orbitals of the dienophile. The reaction scheme for the diels alder reaction can be seen below.

Optimising the reactant of the ethene/butadiene cycloaddition
For the optimisation the reactants were drawn separately on GaussView and were individually subjected to an initial semi empirical AM1 method. The optimisation resulted in the energy values displayed below.
| Reactant | Total energy (a.u) | RMS Gradient (a.u) |
|---|---|---|
| Ethene [37] | 0.02619 | 0.00003328 |
| Cis-Butadiene [38] | 0.04880 | 0.00001429 |
The RMS gradients suggest that a minimum energy conformation was found as the gradient of the potential energy curve converged to 0. The HOMO and LUMO for each reactant was calculated on gaussview. This analysis may elucidate the reaction mechanism as these orbitals are intrinsically involved in the reaction. We Know that in order for orbitals to interact they must have the same symmetry withe respect to the plane.
The molecular orbitrals can be seen in the table below
| Molecular orbital | Ethene [39] | Orbital energy (a.u) | Cis-Butadiene[40] | Orbital Energy (a.u) |
|---|---|---|---|---|
| HOMO |  |
0.05284 |  |
0.01708 |
| LUMO |  |
-0.38775 |  |
-0.34382 |
It is clearly shown above that the HOMO of ethene is symmetric with respect to the plane. Whereas the LUMO is antisymmetric with respect to the plane. It is clear that the HOMO for cis butadiene is antisymmetric with respect to the plane, with its LUMO being symmetric with respect to the plane. Therefore, in both cases the HOMO is the bonding orbital leaving the LUMO orbital as an anti-bonding orbital. Thus, as the HOMO of ethene and the LUMO of cis-butadiene are of the same symmetry with respect to the plane. Thus we would expect the reaction to proceed as we observe quite significant favorable electronic interactions.
Optimisating the Transition state for the Ethene/Butadiene cycloaddition
The AM1 optimised reactant molecules were both copied onto a new guassview window and were manipulated until they resembled the expected transition state with the ethene above the butadiene. The transition state was then modeled using the frozen coordinate method as very little computational required for relatively accurate results. Firstly, the terminal bond distances were set to 2.00A and the terminal redundant coordinates were set to frozen bonds. This was then optimised under the AM1 method. Once the calculation had completed the two frozen bonds were unfrozen and the derivative option was chosen to allow the optimisation of the transition state. The Opt+freq method was then selected with the additional keyword Opt=Noeigen. This would prevent the calculation from terminating after obtaining imaginary frequencies. The predicted IR spectrum under the AM1 method is shown below. Furthermore, the more accurate DFT -B3LYP/6-31G* method will be used to evaluate the difference in accuracy between the DFT and AM1 methods under the same procedure. The imaginary vibration associated with the formation of the two new σ bonds was found at -956.14cm-1 for AM1 and -525cm-1 for DFT can be seen below.
| AM1 | DFT |
|---|---|
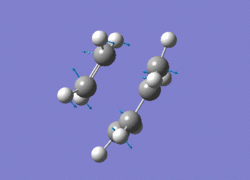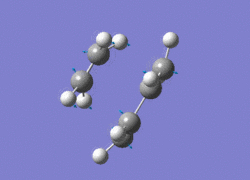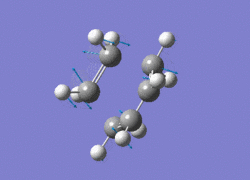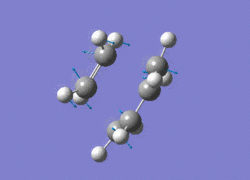 |
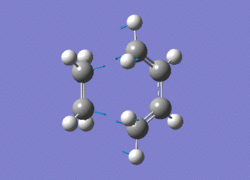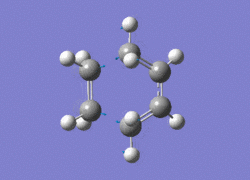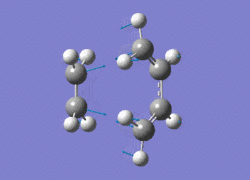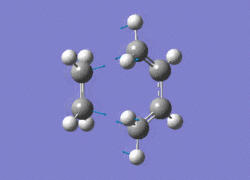 |
It is clearly shown that under each method very similar transition structures are formed which will be compared later. However, the imaginary frequency which corresponds to reaction coordinate of the transition state is significantly shifted for the DFT method. Assuming no calculating error this suggests that the imaginary frequency should in fact be less negative than -956cm-1. The table below summarizes the frequency analysis
| Method | Total Energy (Ha) | RMS gradient | Frequency of imaginary vibration (cm-1) | Intensity |
|---|---|---|---|---|
| AM1 [41][42] | 0.11165 | 0.00001166 | -956 | 6 |
| DFT [43][44] | -234.54390 | 0.00001064 | -525 | 6 |
The two methods have yielded different imaginary frequencies. The presence of this mode alone suggests the successful identification of the transition state structure. In both vibration there is a concerted movement of the terminal carbons moving towards each other and forming two new σ bonds. This motion supports what we would expect to see for a pericyclic reaction involving the concerted movement of electrons. the lowest vibrational mode for the DFT method was found at 135cm-1 and 147 for the AM1 method. This vibration shows the ethene unit rotating around a fixed axis, above the cis-butadiene. This motion which is depicted below suggests a non concerted movement of electrons because of the assymmetric lengthening and shortening of the two new σ bonds, contradicting the theory behind pericyclic reactions.

The HOMO and LUMO of the transition states were visualized on GaussView and can be seen in the below table.
| Molecular orbital | AM1 [45] | Energy (a.u) | DFT [46] | Energy (a.u) |
|---|---|---|---|---|
| HOMO-1 |  |
-0.36351 |  |
-0.37135 |
| HOMO |  |
-0.35034 |  |
-0.35169 |
| LUMO |  |
-0.15699 |  |
-0.16165 |
| LUMO+1 |  |
-0.15290 |  |
-0.14916 |
The Molecular orbitals shown above correlate extremely well with each other and are extremly similar. For both methods the HOMO and LUMO+1 are both symmetric withe the LUMO and HOMO+1 being anti symmetric. We can see from the energy values that the two methods result in the same ordering of the molecular orbitals with slightly different energy values. However, due to the small separation in energy between MO's we would expect some MOs to freely swap positions. Furthermore, both methods have accurately predicted that both the HOMO and LUMO+1 are bonding. From MO orbital theory we know that the Molecular orbitals of transition state are a result of a combination of molecular orbitals from the reactants. Thus we can use this to determine the contributions from the two reactant orbitals to the transition state MOs. However, this comparison can will only be made for the AM1 Molecular orbitals which should produce accurate results as the DFT method gave the same results.
Furthermore the table below compares the geometric parameters of AM1 and DFT optimised transition states.
| Method | Forming C-C distance (A) | Diene C=C bond length | Diene C-C bond length (A) | Ethene C=C bond length (A) |
|---|---|---|---|---|
| AM1 [47][48] | 2.12 | 1.38 | 1.40 | 1.38 |
| DFT-B3LYP/6-31* [49][50] | 2.27 | 1.38 | 1.41 | 1.39 |
The above comparison of the two methods shows the main difference is between the forming C-C bond distance. the remaining bond lengths are nearly identical for both methods. Literature identifies the C-C bond length as 1.53A and the C=C bond as being 1.33A[51]. The C-C single bond is slightly shorter than literature and the C=C bond is slightly longer than literature. This difference suggests that despite using the more accurate DFT B3LYP/6-31* the results are not always completely accurate. In addition, the C=C double bond may be slightly longer than we would expect due the conjugation of the molecule. This conjugation should weaken C=C double bonds as electron density is distributed over the entire molecule, homogenizing bond length to an extent.
Furthermore, the van der waals radius for Carbon is 1.70A [52]. Therefore, we would expect the non bonding distance between two terminal carbons would be around 2*1.70=3.40A. Thus, the forming C-C bonds in the transition state are roughly half way between the non bonding distance and the C-C single bond distance, suggesting that there is an interaction between the two pairs of terminal Carbons, which will eventual form the new σ bonds.
IRC calculations
In this section the intrinsic reaction coordinate method will be used to follow the minimum energy path from the transition state to a local minimum structure associated with the product of the reaction. Due to calculation time constraints the IRC calculation will employ the AM1 Optimised transition states. This is because the AM1 method has been previously proved proved to be relatively accurate, giving results extremely similar to the more sophisticated DFT-B3LYP/6-31G* method. The IRC method calculated the the force constant "always" for the forward reaction, with the maximum number of steps being set to 80. The figures below display the variation of the total energy and the RMS gradient at each step as well as the final product structure. the IRC converged to local minimum structure after 27 steps.

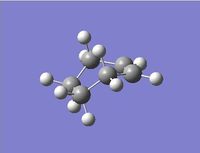
We can see from the above results that the calculation had successfully converged to a minimum structure. On inspection of this minimum structure we see our expected product, supporting a successful calculation. Overall, the above results agree with what we expect from theory.
Optimisation of the Reactant for the Cyclohexadiene/Maleic Anhydride
In this part of the report another interesting Diels alder reaction between maleic anhydride and cyclohexadiene will be analyzed. In this reaction we will explore the endo and exo selectivity associated with this type of reaction. It is well documented that under kinetic control the endo product will predominate and under thermodynamic control the exo product dominates. The figures below shows the geometric difference between the exo and endo products aswell as the reaction coordinate for kinetic vs thermodynamic control.
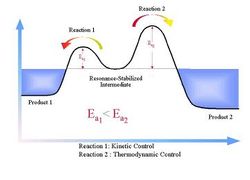
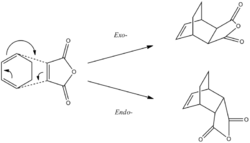
For the Cyclohexadiene we observe a puckering of the ring structure. This is most most likely caused by the differing sp2 and sp3 hybridization of the Carbon centers, resulting in different bond lengths within the ring. However, in order to accurately model the transition state the ideal planer cyclohexadiene was required. Thus, instead of building the molecule from carbon centers, a planer benzene template was modified and optimised under the same semi empirical AM1 method. Both transition states will be modeled using techniques that have been previously explored using the optimised planer cyclohexadiene. The geometry of the reactant was optimised using the semi empirical AM1 method. The table below shows the energy values and and 3D jmol images.
| Name of reactant | 3D image | Total energy (a.u) | RMS gradient | Point Group |
|---|---|---|---|---|
| Cyclohexadiene [54] | Click Here | 0.0277 | 0.00000767 | C2 |
| Planer cyclohexadiene [55] | Click Here | 0.0280 | 0.00005261 | C2v |
| Maleic Anhydride [56] | Click Here | -0.1218 | 0.00010389 | C2v |
The low RMS gradients suggest that a minimum energy conformation has been successfully found. Furthermore, the HOMO and LUMO and their corresponding energy values of both of the reactants can be seen below.
| Molecular Orbital | Cyclohexadiene [57] | Energy (a.u) | Maleic Anhydride [58] | Energy (a.u) |
|---|---|---|---|---|
| LUMO |  |
-0.19081 |  |
-0.21457 |
| HOMO |  |
-0.32251 |  |
-0.34751 |
The HOMO of cyclohexadiene is Anti symmetric with respect to the plane and the LUMO is symmetric with respect to the plane. Furthermore, the HOMO of maleic anhydride is symmetric with respect to the plane and the LUMO is anti symmetric with respect to the plane.
Thus, in cyclohexadiene the HOMO is the bonding orbital and the LUMO is the anti bonding orbital. For maleic anhydride only the LUMO is bonding. Thus the molecular orbitals analysis suggests a bonding interaction between the HOMO of cyclohexadiene and the LUMO of maleic anhydride.
Optimising Transition States for the Cyclohexadiene/Maleic anhydride Cycloaddition
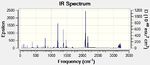
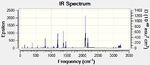
The frozen coordinate method was successfully used to model the transition state for the reaction between ethene and cis-butadiene. Therefore, this method will be employed for this section in order to accurately measure the transition states. Thus, after the reactants were optimised separately they were both copied onto a new window and manipulated to resemble the exo and endo transition states. The distance between the terminal carbon atoms was then set to 2.20A and the rest of the transition state was then optimised. On completion the terminal bonds were given the derivative option and the transition state was optimized again to a Berny Transition state using the Opt+Freq AM1 method. The IR spectrum, imaginary vibrational mode and lowest positive vibration of the transition states are shown below.
| Endo IR spectrum | Exo IR spectrum |
|---|---|
 |
 |
| Transition state | Imaginary vibration | Lowest Positive Vibration |
|---|---|---|
| Endo [59][60] | 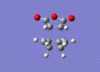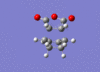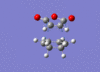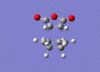 |
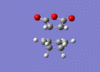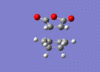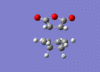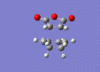 |
| Exo [61][62] |  |
 |
The imaginary vibrational modes are what we would expect to see as they depict the concerted formation of the two new C-C σ bonds. As with ethene and cis butadiene the lowest positive frequency displays a non concerted formation between the two pairs of terminal carbon atoms. Nevertheless, the overall frequency analysis is summarized below.
| Transition state | Energy (Ha) | RMS gradient | Vibration description | Frequency cm-1 | Intensity |
|---|---|---|---|---|---|
| Endo [63][64] | -0.0515 | 0.00004474 | Imaginary vibration | -807 | 71 |
| Endo | - | - | Lowest Positive Vibration | 62 | 2 |
| Exo [65][66] | -0.0504 | 0.00011141 | Imaginary vibration | -813 | 96 |
| Exo | - | - | Lowest Positive vibration | 60 | 1 |
The AM1 method identifies the endo transition state as that being the lowest energy transition state. This observation supports the endo product as the Kinetic product as it proceeds via lower energy transition state with low a lower activation energy. However, in order to evaluate this observation in more detail the more accurate DFT-B3LYP/6-31G* method will be used. The table below tabulates the 3D jmol and total energies Under the DFT optimisation.
| Transition state | Energy (a.u) | RMS gradient | Point group | Imaginary frequency |
|---|---|---|---|---|
| Exo [67][68]Click Here | -612.6793 | 0.00002901 | Cs | -448.38 |
| Endo [69][70]Click Here | -612.6833 | 0.00003077 | Cs | -446.63 |
We can see that despite using the more accurate DFT-B3LYP/6-31G* method the endo product is still the most stable transition state, supporting the endo product as the kinetic product. However, it is clear that the DFT method shift the imaginary frequency to more positive wave numbers. Furthermore, both the DFT and AM1 method the output transition structures are slightly different. This difference arises because each of the methods optimises a different molecular parameter. For the DFT-B3LYP/6-31G* method the reactant molecules are optimised to reduce steric interactions. This is achieved by bending the structure to a position where the carbon atoms that are not involved in the reaction are away from those that are involved. The table below compares the geometric parameters between the DFT and AM1 optimised structures.
| Transition state and method | Anhydride C=C bond length (A) | Anhydride C=O bond length (A) | Cyclohexadiene C-C bond length (A) | Cyclohexadiene C=C bond length (A) | Forming C-C distance A |
|---|---|---|---|---|---|
| Exo DFT [71][72] | 1.40 | 1.20 | 1.51 | 1.39 | 2.29 |
| Exo AM1 [73][74] | 1.41 | 1.22 | 1.49 | 1.39 | 2.17 |
| Endo DFT [75][76] | 1.41 | 1.20 | 1.52 | 1.41 | 2.27 |
| Endo AM1 [77][78] | 1.41 | 1.22 | 1.49 | 1.39 | 2.16 |
For this reaction each method has predicted fairly different results for the bond length in the transition states. The DFT-B3LYP/6-31G* method predicts much larger inter-atomic distances perhaps due to minimizing steric repulsions. The difference between the other bond lengths is most likely due to the differing transition state structures for each method.
Molecular orbital Analysis
| Molecular orbital | Exo tansition state [79] | Endo transition state [80] |
|---|---|---|
| LUMO+1 (side view) |  |
 |
| LUMO+1 (bottom view) |  |
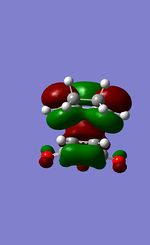 |
| LUMO |  |
 |
| HOMO |  |
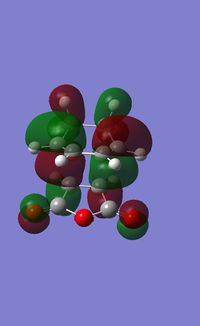 |
| HOMO-1 |  |
 |
For the endo transition state both the LUMO+1 and HOMO-1 are symmetric iwth respect to the plane. The LUMo and HOMO are both anti symmetric with respect to the plane. For the exo transition state the same symmetry is observed with both the LUMO+1 and the HOMO-1 being symmetric and the LUMO and HOMO being antisymmetric with respect to the plane. For both transition states the HOMO and HOMO-1 energy levels are occupied bonding orbitals, whereas the LUMO and LUMO+1 are both unoccupied non bonding orbitals.
An important secondary electronic interaction can be seen in the LUMO+1 molecular orbital. It is clear that the carbonyl groups on the maleic anhydride interact with the Orbitals on Cyclohexadiene for both transition states. Literature uses this interaction to account for the regio-selectivity of the reactions[81]. The reason for this is that a much better overlap is seen in the endo transition state making this the prefered kinetic product.

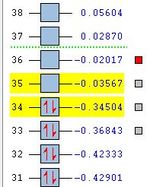
Furthermore, as each MO is a combination of a HOMO and a LUMO from the reactants we can approximate the reactant contributions to the molecular orbitals in the transition state. As we have previously modeled the HOMO and LUMO, we will use these in this analysis. Perhaps if more time were available the deeper orbitals of the reactant could be analyzed and used to accurately model the contributions. We would expect the Molecular Orbitals of the transition state to be a result of the following contributions from the reactants.
(LUMO + 1) = Maleic Anhydride (HOMO) + Cyclohexadiene (LUMO)
(LUMO) = Maleic Anhydride (LUMO) + Cyclohexadiene (HOMO)
(HOMO) = Maleic Anhydride (LUMO) + Cyclohexadiene (HOMO)
(HOMO - 1) = Maleic Anhydride (HOMO) + Cyclohexadiene (LUMO)
The Molecular orbital energy summaries can be seen on the right. We can see that the bonding orbitals (HOMO and HOMO-1) are relatively similar in energy. However, it is likely that we are ignoring some secondary orbital interactions present in the LUMO+1 and the HOMO-1, which may effect the reliability of these results. Therefore, this analysis will serve only as a rough qualitative evaluation.
IRC analysis
In this section of the module we will once again use IRC analysis to locate a local minimum corresponding to the product molecule for both the endo and exo transition states. Due to calculating time constraints the IRC calculation will employ the AM1 Optimised transition states. This is because the AM1 method has been previously proved proved to be relatively accurate, giving results extremely similar to the more sophisticated DFT-B3LYP/6-31G* method. The calculation, involved calculating the force constant "always" in the forward direction with the maximum number of steps set to 90. We will begin this section by analyzing the endo results which converged to local minimum after 26 steps. The IRC graphs and the final product structure can be seen below.

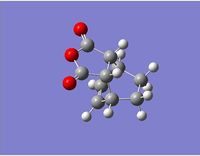
We can see from the above results that the endo IRC calculation successfully converged to local minimum structure corresponding to the endo product. These results suggest the successful modelling of the endo transition state. The results for the exo transition state can be seen below

We can see that the exo transition state successfully converged to a local minimum to the corresponding Exo product after 24 steps. Thus as stated before these results support the successful modelling of the Exo transition state.
Conclusion
Throughout this module we have employed various computational techniques to predict the transition state structures and extract various important parameters. The AM1 method proved to a fast and powerful method to be able to roughly predict molecular orbitals, imaginary frequencies and optimised geometries. However, the DFT-B3LYP/6-31G* method proved to be a more accurate method at the expense of computing time. Thus, though the DFT method provided more accurate thermochemical data, it would be extremely time consuming to apply this method to larger molecular systems.
Overall, the computational techniques that have been employed in this report has enabled us to analyze a chemical reaction from its reactants through to the transition states to the products with relatively good accuracy. Thus, when starting a chemical reaction experimentally, computational techniques can be used initially to elucidate stereo chemical outcomes and favorable reaction pathways. Finally, the imaginary frequencies obtained support the notion that pericyclic reactions proceed in a concerted manor.
References:
- ↑ DOI:10.1021/ja00101a078
- ↑ H.Rzepa, 2nd Year Organic Lecture Course - Conformational Analysis, 2011, Lecture 2
- ↑ http://hdl.handle.net/10042/to-12433
- ↑ H.Rzepa, 2nd Year Organic Lecture Course - Conformational Analysis, 2011, Lecture 2
- ↑ http://hdl.handle.net/10042/to-12432
- ↑ File:HAXADIENE ANTI OPTDFTB3LYP FREQ.LOG
- ↑ http://hdl.handle.net/10042/to-12431
- ↑ J. Coates, Encyclopaedia of Analytical Chemistry, R. A. Meyers (Ed.), 2000, pp 10815 - 10831
- ↑ http://hdl.handle.net/10042/to-12433
- ↑ File:HAXADIENE ANTI OPTDFTB3LYP FREQ.LOG
- ↑ http://hdl.handle.net/10042/to-12435
- ↑ http://hdl.handle.net/10042/to-12432
- ↑ File:HAXADIENE ANTI OPTDFTB3LYP FREQ.LOG
- ↑ http://hdl.handle.net/10042/to-12431
- ↑ http://hdl.handle.net/10042/to-12441
- ↑ http://hdl.handle.net/10042/to-12440
- ↑ http://hdl.handle.net/10042/to-12442
- ↑ http://hdl.handle.net/10042/to-12437
- ↑ http://hdl.handle.net/10042/to-12426
- ↑ http://hdl.handle.net/10042/to-12438
- ↑ http://hdl.handle.net/10042/to-12439
- ↑ http://hdl.handle.net/10042/to-12429
- ↑ http://hdl.handle.net/10042/to-12657
- ↑ http://hdl.handle.net/10042/to-12656
- ↑ http://hdl.handle.net/10042/to-12652
- ↑ http://hdl.handle.net/10042/to-12653
- ↑ 3rd Year Computational Chemistry Online Lab Manual, Module 3, 2011
- ↑ http://hdl.handle.net/10042/to-12439
- ↑ http://hdl.handle.net/10042/to-12437
- ↑ http://hdl.handle.net/10042/to-12459
- ↑ http://hdl.handle.net/10042/to-12446
- ↑ 3rd Year Computational Chemistry Online Lab Manual, Module 3, 2011
- ↑ http://hdl.handle.net/10042/to-12439
- ↑ http://hdl.handle.net/10042/to-12437
- ↑ http://hdl.handle.net/10042/to-12459
- ↑ http://hdl.handle.net/10042/to-12446
- ↑ http://hdl.handle.net/10042/to-12336
- ↑ http://hdl.handle.net/10042/to-12337
- ↑ http://hdl.handle.net/10042/to-12336
- ↑ http://hdl.handle.net/10042/to-12337
- ↑ http://hdl.handle.net/10042/to-12425
- ↑ http://hdl.handle.net/10042/to-12443
- ↑ http://hdl.handle.net/10042/to-12444
- ↑ http://hdl.handle.net/10042/to-12445
- ↑ http://hdl.handle.net/10042/to-12443
- ↑ http://hdl.handle.net/10042/to-12444
- ↑ http://hdl.handle.net/10042/to-12425
- ↑ http://hdl.handle.net/10042/to-12443
- ↑ http://hdl.handle.net/10042/to-12444
- ↑ http://hdl.handle.net/10042/to-12445
- ↑ D. R. Lide, Tetrahedron, 17, 1962, pp 125 - 134
- ↑ A. Bondi et al., J. Phys. Chem., 68 (3), 1964, pp 441 - 451
- ↑ http://hdl.handle.net/10042/to-12607
- ↑ http://hdl.handle.net/10042/to-12447
- ↑ http://hdl.handle.net/10042/to-12466
- ↑ http://hdl.handle.net/10042/to-12448
- ↑ http://hdl.handle.net/10042/to-12468
- ↑ http://hdl.handle.net/10042/to-12467
- ↑ http://hdl.handle.net/10042/to-12564
- ↑ http://hdl.handle.net/10042/to-12565
- ↑ http://hdl.handle.net/10042/to-12563
- ↑ http://hdl.handle.net/10042/to-12566
- ↑ http://hdl.handle.net/10042/to-12564
- ↑ http://hdl.handle.net/10042/to-12565
- ↑ http://hdl.handle.net/10042/to-12563
- ↑ http://hdl.handle.net/10042/to-12566
- ↑ http://hdl.handle.net/10042/to-12567
- ↑ http://hdl.handle.net/10042/to-12569
- ↑ http://hdl.handle.net/10042/to-12568
- ↑ http://hdl.handle.net/10042/to-12570
- ↑ http://hdl.handle.net/10042/to-12567
- ↑ http://hdl.handle.net/10042/to-12569
- ↑ http://hdl.handle.net/10042/to-12563
- ↑ http://hdl.handle.net/10042/to-12566
- ↑ http://hdl.handle.net/10042/to-12568
- ↑ http://hdl.handle.net/10042/to-12570
- ↑ http://hdl.handle.net/10042/to-12564
- ↑ http://hdl.handle.net/10042/to-12565
- ↑ http://hdl.handle.net/10042/to-12563
- ↑ http://hdl.handle.net/10042/to-12564
- ↑ I. Fleming, Frontier Orbitals and Organic Chemical Reactions, John Wiley & Sons Ltd, 2002, pp 106 - 108
- ↑ http://hdl.handle.net/10042/to-12609
- ↑ http://hdl.handle.net/10042/to-12609
- ↑ http://hdl.handle.net/10042/to-12610
- ↑ http://hdl.handle.net/10042/to-12610
