Rep:Mod3TRANSITIONSTRUCTURES:DanielPohoryles
Optimizing the Reactants and Products
1,5-hexadiene with anti-linkage was drawn on gaussview, the following was obtained from HF/3-21G optimisation (“React_anti”). Memory limit was set to 500 MB.
For comparison 1,5-hexadiene with gauche-linkage was drawn on gaussview, the following was obtained from HF/3-21G optimisation (“React_gauche”). Memory limit was set to 500 MB.
It is expected to have higher energy due to steric repulsion which is supposedly higher in the gauche form.
The gauche molecule has a higher energy than the anti, which was expected. The Pointgroup obtained is the same. The molecule corresponds to the gauche4 structure in the Appendix of the wiki.
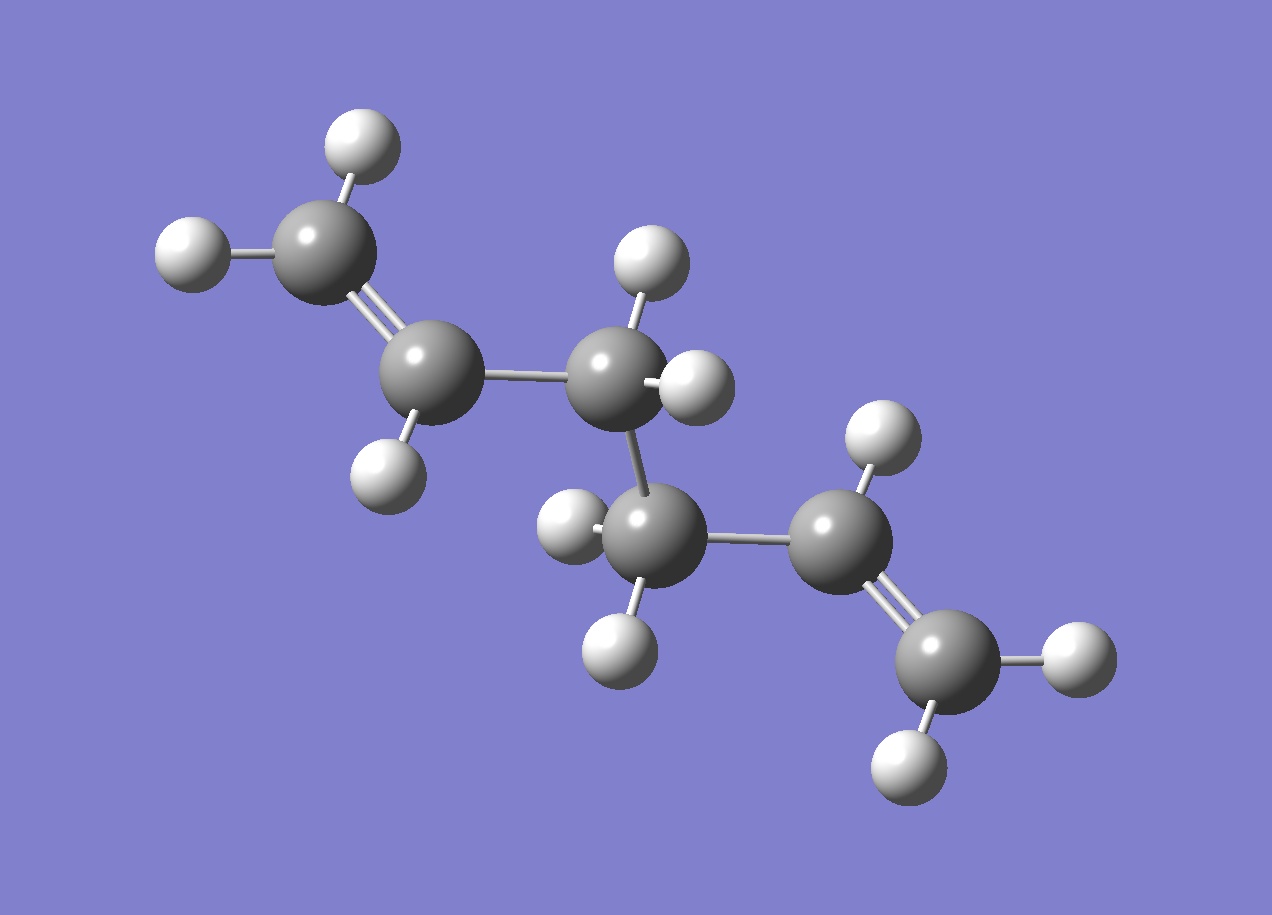
To get lowest energy conformation, we must try to reduce steric hindrance between the atoms and the obtained structure from HF/3-21G optimisation is the following, corresponding to the anti2 structure in the Appendix of the wiki.
This structure is actually not the lowest in energy of three optimised structures. The first one, react_anti, is lower in energy and cannot be found in the Appendix1 of the wiki. It is basically a mirror image (diastereoisomer) of anti1, which is the lowest energy anti-structure found in the table. Actually the lowest energy conformer is gauche in linkage!
React_anti2 was re-optimised using the B3LYP/6-31G* optimisation
The general aspect of the outputs of the two different levels of calculations is the same; however bondlenghts and angles are quite different (±0.1A and ±1°)!
A frequency calculation using the same parameters is carried out (react_anti2_B3LYP_6-31G_freq). This was performed to check if the structure corresponds to an actual minimum (all frequencies need to be positive) as the frequency corresponds to the derivative of the potential energy plot. It also allows to compare the energies with experimentally measured quantities as this requires some additional terms that are included by frequency analysis.
The frequency check showed that the molecule really corresponds to a minimum: only positive vibrations were obtained. The IR spectrum was simulated.
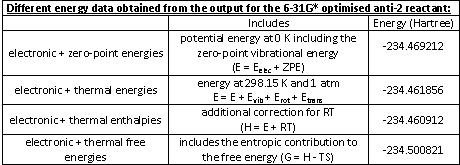
From the OUTPUT file the following data was noted:
Optimizing the "Chair" and "Boat" Transition Structures
1. OPTIMIZING THE CHAIR TRANSITION STRUCTURE
An allyl fragment (CH2CHCH2) corresponding to half of the transition state structures was drawn in gaussview and optimised using the HF/3-21G level of theory ->TRANSITIONSTATE_ALLYL_FRAGMENT
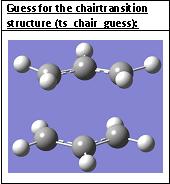
A new mol group is created (ts_chair_guess) from two allyl fragments oriented so as two form the chair transition state:
The distance between the terminal ends of the allyl fragments was set to 2.2 A.
The chair transition state was optimised using two different methods:
- a) As we have a reasonable guess for the transition structure geometry, the force constant matrix (also known as the Hessian) can be computed in the first step of the optimization which will then be updated as the optimization proceeds
The chair transition state is optimised using the Opt+Freq calculation, using the HF/3-21G level of theory, changing Optimization to a Minimum to Optimization to a TS (Berny), calculating the force constants Once and typing Opt=NoEigen in the Additional keyword box at the bottom (stops the calculation crashing if more than one imaginary frequency is detected during the opt).
The calculation was successful giving the following optimised structure and an imaginary frequency at 818 cm-1 which corresponds to the Cope rearrangement:
- b) It is possible to generate a better transition structure by freezing the reaction coordinate (using Opt=ModRedundant and minimizing the rest of the molecule). Once the molecule is fully relaxed, the reaction coordinate can then be unfrozen and the transition state optimization is started again. This has as advantage that it may not be necessary to compute the whole Hessian once this has been done, which reduces the computational time needed.
To optimise the transition structureusing the frozen coordinate method, the guess structure was edited. A new coordinate is created in the Redundant Coord Editor of GaussView. The two bonds that are broken/formed in the Cope rearrangement are frozen and set to 2.2 A. The optimisation job “TS_CHAIR_OPT_2frozencoordinate” was submitted using the HF/3-21G level of theory.
Very similar to the previously obtained optimised structure. The bond distances between the fragments are fixed to 2.2 A.
In the Redundant Coord Editor, the two bonds that were frozen in the previous step are not frozen but instead the option “Derivative” was chosen this time. A transition state optimisation job is prepared using the HF/3-21G level of theory again. Unlike the first transition state optimisation (a), the force constants are not calculated.
2. OPTIMIZING THE BOAT TRANSITION STRUCTURE
The previously optimised Ci anti2 structure is used as reactant. To this is added again the same structure which will be the product structure.
The reactant and product were displayed and numbered in the following way:
A Opt+Freq, QST2 optimisation is set-up, this fails however because the calculation is just interpolating between the two structures, this will never locate the boat transition structure.
The geometries of reactant and product are adapted to obtain the two structures below. The central C-C-C-C dihedral angle was set to 0° and the two inside C-C-C angles were reduced to 100°.
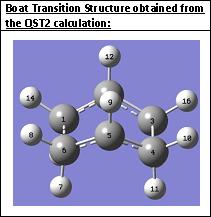
Now the QST2 calculation was lauched for the structures that are closer to the transition structure geometry. The job was completed this time. This shows that the QST2 calculation has a problem to calculate the transition state if the reactant and product are not close to the transition structure geometry. The boat transition structure was obtained from the calculation:
For the frequency calculation only one imaginary frequency at 840 cm-1 was obtained; it corresponds to the cope rearrangement:
3. ANALYSING THE DIFFERENT REACTION PATHS AND THEIR OUTCOMES USING THE IRC METHOD
In order to determine which transition state corresponds to the cope rearrangement of which conformers of 1,5-hexadiene, it is necessary to use the computational IRC method. A simple guess is impossible to make, all the factors affecting this rearrangement cannot be simplified.
To start with, the reaction path obtained from the HF/3-21G optimised chair transition structure obtained from the force constant matrix method was analysed. The IRC calculation was set to include 50 points and to calculate the force constant at every step in order to get a more accurate result for the calculation. As the cope rearrangement is symmetrical only the forward path was analysed as it is the same as the backwards one.
The obtained conformer from this IRC analysis is “gauche2”:
4. CALCULATION OF ACTIVATION ENERGIES FOR THE REACTION PROCEEDING VIA THE BOAT AND THE CHAIR TS
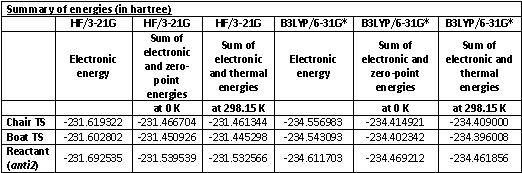
First the two transition structures were re-optimised using the B3LYP/6-31G* level of theory and a frequency analysis was performed. From the log file, the energies at 0 and 298.15K can be obtained and compared to the values found for the 3-21G level of theory.
In the image below the geometries of the transition structures obtained from B3LYP/6-31G* level of theory can be seen. If they are compared to the previous structures obtained from the lower level of theory (see pictures earlier in this report), no real difference can be seen. There is though a difference in the bond lengths of the bonds that are forming/breaking, which are shorter for the chair structure and longer for the boat structure. The structures obtained from the new level of theory are hence very similar in geometry, but very different, namely much lower, in energy.
The results are summarised in the tables below.
It can clearly be seen that the B3LYP/6-31G* level of theory is needed to get close to experimental values. In order to be able to compare computational results to actual experimental values it is not possible to use the low level HF/3-21G. The low level of symmetry is a good first step as it is computationally far less expensive.
The Diels Alder Cycloaddition
In this part the transition structures of Diels-Alder reactions will be characterised using the force constant matrix method described in the previous part of this report. The shape of the frontier molecular orbitals which govern Diels Alder Cycloadditions will also be discussed and analysed computationally. The HOMOs and LUMOs of the diene and the dienophile are crucial to determine if the reaction can occur in a concerted stereospeciphic fashion or not.
The reaction is only allowed if the HOMO of one reactant can interact with the LUMO of the other one. However the HOMO-LUMO can only interact if they overlap significantly. Hence the reaction is forbidden if the orbitals have different symmetry properties as no overlap density is possible.
Furthermore substition of one of the involved species will clearly affect the reaction if they have π orbitals that can interact with the new orbitals formed. This can lead to a different stereochemistry of the reaction. This secondary orbital effect will also be analysed in this part of the report.
1) Optimisation of cis-butadiene and ethylene and analysis of its FMOs
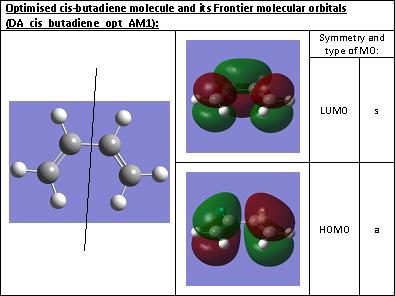
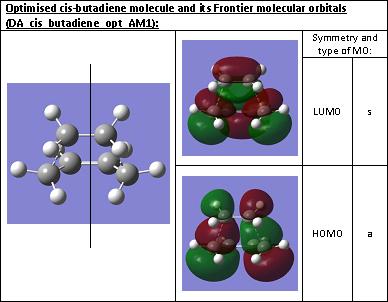
First cis-butadiene was optimised using the semi-empirical AM1 method. The structure calculated is shown below. The molecular orbitals were also calculated and the HOMO and LUMO were visualised. The symmetry of the HOMO and LUMO with respect to the designated plane of symmetry (see structure of the molecule) were determined and reported on the table below.
The symmetry of the HOMO and LUMO were determined. The HOMO is asymmetric with respect to the plane of symmetry which cuts perpendicularly through the axis of the single bond. The LUMO, on the other hand, is symmetric with respect to this plane.
The same optimisation was performed for ethylene in order to analyse the frontier MOs of this compound just as it was done for cis-butadiene:
Again the symmetry of the HOMO and LUMO were determined. Exactly the opposite of the cis-butadiene was observed. The HOMO is symmetric with respect to the plane of symmetry which cuts perpendicularly through the axis of the single bond. The LUMO, on the other hand, is assymmetric with respect to this plane.
2) Optimisation of the transition structure of the Diels-Alder Reaction and analysis of FMOs
As we have a good guess already for the Transition structure the using the force constant matrix method was chosen to optimise the transition structure. The guess Transition structure was drawn on GaussView and then optimised to a TS (Berny) using the semi-empirical AM1 method. The interfragment distance was set to 2.1A for the guess structure. Furthermore the options were set to calculate the force constants Once and by typing Opt=NoEigen in the Additional keyword box at the bottom the calculation is prevented from crashing if more than one imaginary frequency is detected during the calculation. In the obtained transition structure the interfragment distance is 2.11925 A.
Typical sp3 C-C bond lengths are 1.53 A and sp2 C-C bond lengths are 1.48 A [1]. The Van der Waals radius of Carbon is 1.70A [2]. The distance in the bond that is forming in the transition structure is larger than these values (2.11925 A).
Analysis of the imaginary vibration
One imaginary frequency was obtained at -956 cm-1. This vibration corresponds to the rapprochement of the ethylene molecule from the top to the cis-butadiene as shown below. The two bonds are forming synchronously. The lowest positive frequency on the other hand corresponds to an asymmetric motion.
Analysis of FMOs
The Molecular Orbitals were then visualised and the HOMO and LUMO are displayed below and their symmetry with respect to the plane of symmetry (which cuts perpendicularly through the axis of the single bond) was assigned.
The symmetry of the HOMO and LUMO of the transition structure were determined to be the same as previously found for cis-butadiene. The HOMO is asymmetric with respect to the plane of symmetry. The LUMO, on the other hand, is symmetric with respect to this plane.
If we compare the HOMO and LUMO of the transition structure to the Frontier MOs analysed previously for the reactants, it can be seen that the asymmetric HOMO corresponds to a combination of the asymmetric cis-butadiene HOMO to which the asymmetric ethylene LUMO is added from the top. The LUMO on the other hand is formed by the combination of the symmetric butadiene LUMO and the symmetric ethylene HOMO. The reaction is hence allowed because the overlap density between the MOs forming the new bond is significant enough. The reaction can hence proceed in a concerted stereospeciphic fashion.
Reaction Path (IRC Calculation)
An IRC calculation was set-up from the checkpoint file of the optimised structure (still using the AM1 semi-empirical method). This was done in order to analyse the reaction path and confirm that the transition state of the Diels-Alder reaction was actually obtained. It was chosen to calculate the IRC in both directions and to recalculate the force constant at each step. A total of 78 frames were obtained and really described the reaction that we are analysing, passing through the expected transition state. The energy vs. Reaction Coordinate plot was also obtained and shows that the reaction proceeds from the product going via a Transition state that is higher in Energy and finally the product is far lower in Energy.
3) Study of the regioselectivity of the Diels Alder Reaction using the reaction of Cyclohexa-1,3-diene with maleic anhydride as example
The two possible endo and exo transition states were drawn on GaussView and optimised using the using the force constant matrix method with the AM1 method. For both transition states one imaginary vibration corresponding to the Diels-Alder Reaction were obtained. The relative energies and structure elements are displayed below.
The exo transition structure is higher in energy as expected. The exo structure is more strained due to the steric repulsion of the maleic anhydride with the -CH2-CH2- fragment. For the exo structure, the H atoms pointing towards the maleic anhydride create a large steric repulsion, as they are even closer to the approaching maleic anhydride than the C-C fragment. On the other hand, for the endo structure, the C-C through space distance is larger between the maleic anhydride and the opposite C=C fragment, resulting in less steric hindrance. However also the Molecular Orbitals have to be considered.
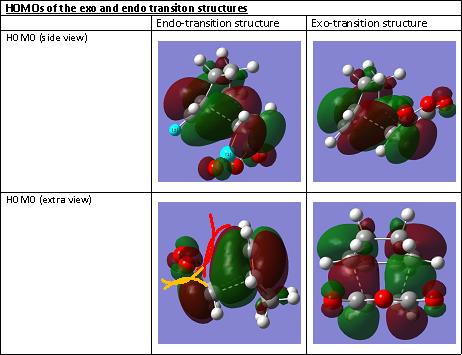
The HOMOs of the two structures were visualised on GaussView and the secondary MO overlap effect was analysed.
In the endo structure, although the steric repulsion between the maleic anhydride and the -CH2-CH2- fragment is non-existant, another destabilising factor is appearing instead. This is the electric repulsion between the Molecular orbitals of the -(C=O)-O-(C=O)- fragment and the remainder of the system. These repulsions (visualised by the red and yellow lines in the “extra view” of the HOMO in the endo structure) lead to the extra nodal planes and hence to a decrease in stability. However this is not significant in comparison to the steric hindrance as the exo structure is still less stable than the endo structure.
Only kinetic factors were used to predict that the endo structure is the more stable product, thermal factors have not been considered. This factor can be significant [3], but will not be discussed here due to lack of time.
References
- ↑ March's advanced organic chemistry: reactions, mechanisms, and structure, Michael Smith and Jerry March, p.24, 6th Edition, http://books.google.com/books?id=cm5s84-GeKMC&pg=PA24&lpg=PA24&dq=literature+value+sp2+C-C+bond+length&source=bl&ots=e4QAcfiauY&sig=r-WLtNjRp-zcJxc40RB7Tr7GHuE&hl=el&ei=G-YmS8uVMsX_4AabkK2dDQ&sa=X&oi=book_result&ct=result&resnum=9&ved=0CDYQ6AEwCA#v=onepage&q=&f=false
- ↑ Carbon Van der Waals radius: Cambridge Crystallographic Data Centre, http://www.ccdc.cam.ac.uk/products/csd/radii/table.php4
- ↑ Bearpark et al., J. Org. Chem., 2003, 68 (19), pp 7158–7166 DOI:10.1021/jo0348827