Rep:Mod3:zy909

Cope Rearrangement

Introduction

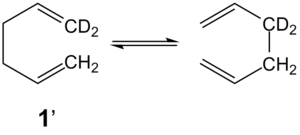
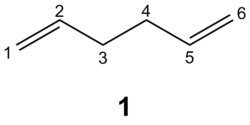
The Cope rearrangement is a [3,3]-sigmatropic rearrangement, belonging to the class of pericyclic reactions. This reaction is studied using 1,5-hexadiene 1 as a model compound, although the reactant and product are symmetrical and hence indistinguishable, preparation of an isotopically labelled sample 1’ reveals isotopic scrambling as a result of equilibration.

As the prototypical sigmatropic rearrangement sharing many structural and mechanistic similarities with other pericyclic reactions, the Cope rearrangement has been the subject of intense mechanistic study. The Woodward-Hoffmann rules and Fukui's work on pericyclic reactions demonstrated that the Cope rearrangement was a concerted process, while Doering and Roth showed elegantly that the reaction was practically stereospecific and involved a chair rather than boat transition state.

Structure Optimisation

Exploring the Conformational Landscape

9 possible conformers exist

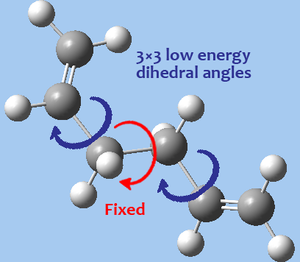
Anti and gauche conformers (about the central C2-C3-C4-C5 dihedral) of 1,5-hexadiene 1 were first optimised at the HF/3-21G level of theory, obtaining two potential conformers. However, the length of the straight-chain carbon skeleton implies that multiple conformers should exist, each corresponding to a local minimum on the potential energy surface. Even if eclipsed conformations about the central dihedral C2-C3-C4-C5 were ruled out, for each of the anti and gauche sets of conformers there are potentially 3 non-eclipsed conformations about the terminal C1-C2-C3-C4 and C3-C4-C5-C6 dihedrals, suggesting a maximum of 9 possible conformers for each of the anti and gauche sets.

Generally, the most stable conformer should be that with the C1-C2-C3-C4 and C3-C4-C5-C6 dihedrals in anti orientations; as C3 and C4 are methylene groups with two protons, two anti orientations exist for each dihedral, giving a total of 4 ideally stable conformers out of the 9 in each set. For the anti set of conformers, the terminal alkenes are far apart to interact significantly, so all 4 of those isomers should be similarly low in energy. For the gauche set, there is likely to be a uniquely stable conformer, in which the terminal alkenes are oriented as far apart from each other.

In addition, due to the symmetry of 1, out of the 9 conformers possible for each of the anti and gauche sets, only 6 are unique in the gauche set, while for the anti set, the additional symmetry introduced by the anti orientation results in there being only 4 unique conformers.

PES scan of dihedral angles (unique conformers circled in yellow)

Anti set of conformers		Gauche set of conformers

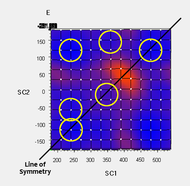
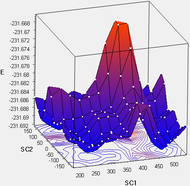
To explore the rotational space about the dihedral angles C1-C2-C3-C4 and C3-C4-C5-C6, scans were performed over the potential energy surface, by using redundant coordinates to fix the central dihedral angle C2-C3-C4-C5 to either 180° (anti) or 60° (gauche), and scan the other two dihedral angles at intervals of 30°. To keep the computational load at a minimum, the scans were performed at the HF/3-21G level. For the anti conformer set, a total of 9 minima were found as expected, as the anti orientation at the central C2-C3-C4-C5 dihedral keeps the terminal alkene groups far apart. For the gauche conformer set, a total of 7 minima were found, with the other 2 potential conformers suffering from repulsive steric interactions between the terminal alkene groups. Nevertheless, it was suspected that these 2 conformers might lie on minima that were unresolved by the scan. 2 guess geometries near these putative conformers were taken from the PES scan and optimised, revealing the 2 missing conformers to be local minima.

Following this, all minima were optimised with HF/3-21G, as the actual conformers are likely to have dihedral angles that deviate away from the multiples of 30° assumed in the scan. The energies and dihedral angles for all 9 conformers are tabulated below, and non-unique, isoenergetic conformers linked by symmetry operations are highlighted in similar colours. Finally, the obtained geometries and energies were compared to the table of conformers provided and matched according to the labels given.

Conformational minima for 1,5-hexadiene (1)

Conformation	Anti				Gauche
	Energy / a.u.	θ / °			Energy / a.u.	θ / °
		1-2-3-4	2-3-4-5	3-4-5-6		1-2-3-4	2-3-4-5	3-4-5-6
a	-231.69253	-114.6	180.0	114.6	-231.69153	-109.4	-63.7	-109.4
b	-231.69097	-114.5	-178.4	-0.2	-231.68962	-121.2	-71.1	-14.2
c	-231.69260	-115.1	-176.9	-115.1	-231.69266	-120.8	-67.7	117.2
d	-231.69097	0.2	178.4	114.5	-231.68962	-14.2	-71.1	-121.2
e	-231.68907	0	180.0	0.0	-231.68772	1.6	-75.8	1.5
f	-231.69097	-0.2	-178.4	-114.5	-231.68916	-1.1	-70.2	139.0
g	-231.69260	115.1	176.9	115.1	-231.69266	117.2	-67.7	-120.8
h	-231.69097	114.5	178.4	0.2	-231.68916	139.0	-70.2	-1.1
i	-231.69253	114.6	-180.0	-114.6	-231.69167	123.9	-64.2	123.9

Unique Conformers

Unique conformers of 1,5-hexadiene (1)

Conformer	Structure	Symmetry	Eelec / a.u.	ΔEelec / kJ mol-1
anti1 (c,g)		C2	-231.69260	0.158
anti2 (a,i)		Ci	-231.69253	0.341
anti3 (e)		C2h	-231.68907	9.426
anti4 (b,d,f,h)		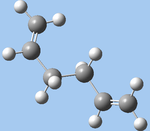C1	-231.69097	4.437
gauche1 (e)		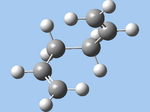C2	-231.68772	12.970
gauche2 (i)		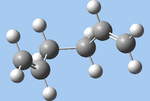C2	-231.69167	2.599
gauche3 (c,g)		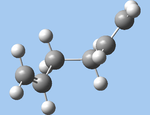C1	-231.69266	0.000
gauche4 (a)		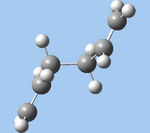C2	-231.69153	2.967
gauche5 (b,d)		C1	-231.68962	7.982
gauche6 (f,h)		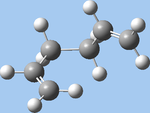C1	-231.68916	9.189

In general, the high-energy conformers are those with syn-periplanar orientations along the C1-C2-C3-C4 and/or C3-C4-C5-C6 dihedrals - see anti3 and gauche1, which have both dihedrals in syn-periplanar orientations. However, on average, the gauche conformers are higher in energy than the anti conformers, due to the unfavourable steric interactions between the terminal alkene groups. For example, even though both anti3 and gauche1 have 2 syn-periplanar interactions, the gauche isomer is less stable due to these steric clashes.

Ground-state Conformer

Subsequently, the anti2 conformer was further optimised at the B3LYP/6-31G(d) level, to provide more accurate energies; anti2 was chosen as a generalised representation of the stable ground-state conformers.

Optimisation of anti2

Method	Eelec / Hartrees	Eelec + ZPE / Hartrees	Eelec + therm + ZPE / Hartrees	H / Hartrees	G / Hartrees	r / Å					θ / °			Low frequencies
						1-2	2-3	3-4	4-5	5-6	1-2-3-4	2-3-4-5	3-4-5-6
HF/3-21G (SPECTRa)	-231.69253	-231.53954	-231.53257	-231.53162	-231.57091	1.32	1.51	1.55	1.51	1.32	-114.6	180.0	114.6	-4	0	0	0	2	3
B3LYP/6-31G(d) (SPECTRa)	-234.61171	-234.46920	-234.46186	-234.46091	-234.50078	1.33	1.50	1.55	1.50	1.33	-118.6	180.0	118.6	-9	0	0	0	4	13
B3LYP/6-31G(d) (tight) (SPECTRa)	-234.61171	-234.46922	-234.46187	-234.46092	-234.50080	1.33	1.50	1.55	1.50	1.33	-118.6	180.0	118.6	0	0	0	2	3	10

The B3LYP method gave lower energies than the Hartree-Fock calculation, as it better models the effects of electron correlation, hence lowering the total electronic energy. Surprisingly though, the initial calculation done with the larger 6-31G(d) basis set turned out to give a less accurate optimisation of the minimum, as the low frequencies were of a much larger magnitude. As such, tight convergence criteria were applied (opt=tight int=ultrafine scf=conver=9), and the optimisation repeated. This reduced the magnitude of low frequencies slightly, and eliminated the negative frequencies, indicating that the minimum has been located; however, the differences in energy and geometry are negligible in this case.

The structures remain largely the same using both HF/3-21G and B3LYP/6-31G(d) methods, with the largest difference manifested in the terminal dihedral angles C1-C2-C3-C4 and C3-C4-C5-C6. With the inclusion of diffuse orbitals in the 6-31G(d) basis set, through-space electronic interactions are modelled more accurately, perhaps counteracting the repulsive steric effects associated with the gauche orientation in those dihedral angles, hence shifting the dihedrals closer to the ideal angle of 120°.

Transition State Search

Chair TS: Berny Algorithm

The Gaussian program implements a modified version of the original Berny algorithm, using polynomial fits of the calculated energies and their first and second derivatives (where available) with respect to molecular coordinates to explore the potential energy surface. Assuming the potential energy surface at the minimum or saddle point (TS) to be quadratic, Newton-Raphson methods may be applied; however, to reduce computational expense, a quasi-Newton method is utilised, updating the Hessian matrix at every step based on the local gradient, rather than performing an expensive recalculation. Simplistically speaking, if the algorithm is currently at the best structure found thus far, it uses the Hessian matrix (second derivatives) to move towards a higher-energy structure; if the algorithm finds this structure to be less optimal than the previous one found so far, it interpolates the two geometries and performs a polynomial fit of the first or second derivatives at both points to identify a guess geometry intermediate to both existing geometries. This process is performed iteratively until convergence is achieved at a saddle point.

The transition state was first approximately constructed with two allyl radical fragments (pre-optimised with HF/3-21G), oriented into a chair structure. The Berny algorithm was then used to search for the actual transition state starting from this geometry. Two methods were used: the first involved starting the Berny algorithm straight from the guess structure; the second was the frozen coordinate method, which froze the distance coordinates of the bonds being formed and broken, minimised the geometry of the rest of the molecule, then unfroze the bonds and ran the Berny algorithm on this partially optimised structure, using the calculated Hessian matrices for those two bonds alone to direct the TS search to vibration along these two coordinates alone.

While the first method of a brute-force search from the guess structure works well for this simple transition state, the method might struggle with poor starting geometries or larger molecules with many more degrees of freedom. In those cases, chemical intuition is necessary to narrow the search within computational limits. This is performed in the second method, where knowledge of the Cope rearrangement is used to identify the bonds being formed and broken. These bond lengths are set to reasonable values for transition states, and the molecule optimised around these geometrical constraints to arrive at a suitable starting geometry for the TS search. Only then is the TS search commenced and directed toward the transition state by specifying the numerical Hessian matrices for the bonds being formed and broken. Both methods arrived at the same transition state geometry and energy.

Finally, the transition state is re-optimised at the B3LYP/6-31G(d) level to obtain a more accurate energy and structure. Having first obtained an approximate transition state with a 3-21G basis set, the subsequent optimisation is faster as the starting geometry is already reasonably close to the 6-31G(d) transition state. This is computationally more efficient as fast calculations can be done first with a small basis set, before a larger basis set is used to improve accuracy.

Vibration

Method	Eelec	ν / cm-1	rC-C
HF/3-21G (unassisted)	-231.61932	-818	2.02
HF/3-21G (frozen coordinate)	-231.61932	-818	2.02
B3LYP/6-31G(d) (tight) (SPECTRa)	-234.55698	-566	1.97

The chair transition state was found to have C_2h symmetry.

With HF/3-21G, the same transition state energies and geometries are obtained through both the unassisted method and the frozen coordinate method, indicating that they have both located the same transition state structure. With B3LYP/6-31G(d), the electronic energy E_elec is lowered due to better modelling of diffuse interactions; however, as the reactant and product energies are similarly lowered upon switching to the 6-31G(d) basis set, it remains to be seen whether the transition state barrier increases or decreases with this basis set. The transition state geometry, in terms of distance between the terminal ends of the allyl fragments, doesn't change significantly between the basis sets. On the other hand, the imaginary frequency changes significantly, indicating that the shape of the potential energy surface around the transition state differs to a large extent between the two basis sets - the lower imaginary frequency with 6-31G(d) implies a gentler slope leading to the saddle point.

Boat TS: QST2 Algorithm

As the Berny algorithm is a quasi-Newton method, which requires a quadratic potential energy surface to find a saddle point, it will only work if a sufficiently good guess geometry is provided initially. This may be easy for small, simple systems or for reactions where analogous transition states have been previously identified; however, the algorithm will fail if the guess geometry is far from the saddle point.

The QST2 (quadratic synchronous transit) method alleviates this problem of guessing the TS geometry, by taking two structures corresponding to reactant and product and quadratically interpolating between these two geometries to get closer to the quadratic region of the PES; quasi-Newton or eigenvector-following methods can then be applied to find the saddle point.

The boat transition state of the Cope rearrangement was located in this fashion, at the HF/3-21G level, by using the anti2 conformer as the reactant structure; the product structure was also derived from the anti2 conformer, except that the atoms were re-numbered to reflect the [3,3]-sigmatropic shift of the C-C bond (see diagram). However, as the reaction path between these two paths is not obvious, involving multiple angle and dihedral rotations, the QST2 job failed to locate any transition state.

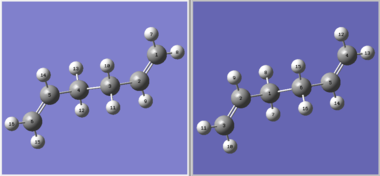
QST2, unaided	QST2, aided

Boat transition state

To assist the algorithm, it was necessary to modify the reactant and product structures to more closely resemble the transition state, so as to provide a straightforward reaction path for analysis by the algorithm. To this end, the central C2-C3-C4-C5 dihedral was set to 0° and the C2-C3-C4 and C3-C4-C5 angles set to 100° in both reactant and product geometries (see diagram). This allowed the boat transition state to be located successfully. Finally, the obtained transition state was re-optimised with B3LYP/6-31G(d).

Method	Eelec	ν / cm-1	rC-C
HF/3-21G	-231.60280	-840	2.14
B3LYP/6-31G(d) (tight) SPECTRa	-234.54308	-532	2.21

The chair transition state was found to have C_2v symmetry.

Just as with the chair transition state, the energy and imaginary vibrational frequency were lowered by switching to the larger 6-31(d) basis set. However, the distance between the terminal ends of the allyl fragments increased on switching basis sets.

Intrinsic Reaction Coordinates

The intrinsic reaction coordinate (IRC) is a minimum-energy path on the potential energy surface connecting the reactant and product geometries and passing through the transition state geometry, perpendicular to the isoenergy contours on the PES. For a given system with zero kinetic energy throughout, this should be the path taken from the saddle point (transition state; highest energy) to the minima on each side of the saddle point (reactant and product); as such, the IRC is a useful tool for confirming that the correct transition state has been identified.

Looking at the structure of the transition state, it is likely that it connects a reaction path between two gauche conformers of 1,5-hexadiene 1. This is inferred from the internal C2-C3-C4-C5 dihedral angle of 0° - it is more likely that the intrinsic reaction coordinate will lead immediately to gauche structures with similarly small dihedral angles of 30°. Moreover, the stable conformer is likely to have both terminal alkene groups in close proximity, with both π faces parallel to facilitate overlap and bond formation in the approach towards the transition state.

IRC plots

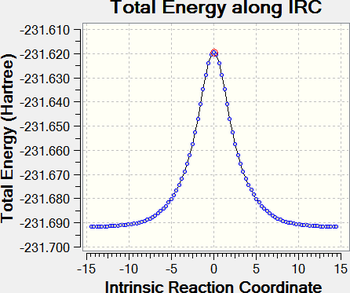
Chair IRC	Boat IRC

IRC calculations were performed at the HF/3-21G level for both the chair and boat transition states, with force constants being calculated at every step. For the chair TS, the IRC leads to the gauche2 conformer, while the boat TS leads to a conformer with a syn-eclipsed central dihedral angle (C2-C3-C4-C5). Consequently, as can be seen from the IRC plots (see above), the chair TS leads to a lower energy minimum than the boat TS. In addition, it may be easily seen that the boat TS has a higher energy than the chair TS, as expected; this shall be discussed in a later section.

Given the unusual prediction of a syn-eclipsed product by the IRC, this was subjected to a frequency calculation, whereupon a negative frequency was found, indicating that the IRC had not stopped at a minimum point, but rather at a maximum. As the IRC terminates when the RMS gradient of the path falls below a certain cutoff, the IRC may terminate at both minimum or maximum points, as long as the turning point plateaus sufficiently such that the gradient of the PES becomes almost flat - this is likely what happened in this case. The syn-eclipsed product was therefore optimised further with HF/3-21G, obtaining the gauche2 conformer as the product, similar to the chair TS.

IRC for Chair TS (selected snapshots)

TS			gauche2

IRC for Boat TS (selected snapshots)

TS			syn-eclipsed conformer

Reaction Activation Energies

The Cope rearrangement activation energies were calculated for both reaction pathways involving the chair and boat transition states respectively. It is expected that the chair pathway will be lower in energy, by analogy to cyclohexane, in which the chair conformation is lower in energy than the boat conformation. This analogy is possible due to the structural similarity between the transition state and cyclohexane.

For comparison with experimental values of the activation energy, which are given in terms of enthalpies, it is necessary to compare the enthalpies (rather than internal energies as instructed by the lab script) of 1,5-hexadiene 1 and the two transition states. The anti2 conformer of 1 is used as a basis for comparison, in line with conventional practice in the literature.

Experimental and calculated activation energies, B3LYP/6-31G(d)

Species	Calcalated, 298 K		Experimental ΔH / kJ mol-1
	H / Hartrees	ΔH / kJ mol-1
1 (anti2)	-234.46092
Chair TS	-234.40804	138.8	140
Boat TS	-234.39507	172.9	187

The close agreement between experimentally measured activation energies and those calculated by an ab initio DFT method demonstrates the accuracy of the calculations, and also provides additional confirmatory evidence for the synchronous, pericyclic pathway involving a chair-like transition state.

Diels-Alder Cycloaddition

Prototype Reaction: Butadiene and Ethene

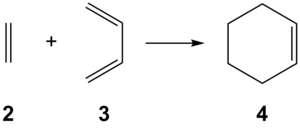
The Diels-Alder reaction is a concerted pericyclic cycloaddition between a conjugated 1,3-diene 2 and an alkene (termed the dienophile) 3, producing a substituted cyclohexene 4. Dienophiles conjugated to electron-withdrawing groups are typically used and coupled to dienes, which may optionally have an electron-donating group. The effect of this is to lower the energy of the LUMO (from the dienophile) while raising the energy of the HOMO (from the diene), reducing the energy difference to enhance the orbital overlap, making the transition state lower in energy and ultimately favouring the reaction.

Structure Optimisation

Ethene 2 and s-cis butadiene 3 were optimised using the semi-empirical AM1 method, and further optimised with HF/3-21G, obtaining planar geometries with horizontal and vertical planes of symmetry.

It was noted that the planar geometry of 3 does not lie at a minimum on the PES, due to a negative frequency identified, corresponding to rotation about the central C2-C3 bond. Perturbation of the geometry about this bond permitted a subsequent optimisation to reach an energy minimum with a non-planar geometry. However, this non-planar conformation is of minor interest as its frontier molecular orbitals are not aligned as well for reaction (see MO analysis below); it is likely that any reaction pathway will convert this non-planar conformation to the planar geometry before passing through the transition state.

Optimisation of ethene 2

Method	Eelec / Hartrees	rC-C / Å
AM1	0.02619	1.33
HF/3-21G	-77.60099	1.32

Optimisation of s-cis butadiene 3

Method	Eelec / Hartrees	rC1-C2 / Å	rC2-C3 / Å	∠C1-C2-C3 / °	θC1-C2-C3-C4 / °
AM1	0.04880	1.34	1.45	125.7	0.0
HF/3-21G	-154.05394	1.32	1.48	126.7	0.0
HF/3-21G (perturbed)	-154.05514	1.32	1.48	124.8	38.2

Molecular Orbital Symmetry

Plane of symmetry in transition state

The frontier molecular orbitals (HOMO and LUMO) of both ethene 2 and butadiene 3 have been visualised. Both AM1 and HF/3-21G calculations gave frontier MOs of the same shape and symmetry; the AM1 MOs are shown in the table below.

To rationalise the reactivity in the Diels-Alder reaction, the symmetry of frontier MOs is considered with respect to the transition state of the reaction (see right). As only molecular orbitals with the same symmetry may overlap and hence lead to the reaction, the symmetry of the frontier MOs of 2 and 3 are considered with respect to the vertical plane of symmetry present in the transition state, and assigned either the label s (symmetric) or a (anti-symmetric).

From the MO diagrams, it is evident that the HOMO of butadiene is able to overlap with the LUMO of ethene due to matching symmetry and orbital phases; the same can be said for the interaction between the HOMO of ethene and the LUMO of butadiene. Consequently, a qualitative analysis of the reactant system suggests that the reaction between 2 and 3 is permitted.

Frontier molecular orbitals of ethene 2 and butadiene 3

Molecule		HOMO	LUMO
Ethene 2	MO
	Symmetry	s	a
	E (AM1) / eV	-0.38775	+0.05284
	E (HF/3-21G) / eV	-0.37970	+0.18659
Butadiene 3	MO
	Symmetry	a	s
	E (AM1) / eV	-0.34381	+0.01707
	E (HF/3-21G) / eV	-0.32529	+0.12353

The smaller the energy difference between two compatible molecular orbitals, the better the overlap and interaction. At the AM1 level, the energy difference between anti-symmetric orbitals (0.39665 eV) is smaller than that for the symmetric orbitals (0.40482 eV), implying that the anti-symmetric interaction is better. At the HF/3-21G level, the converse is true, with a smaller energy difference between symmetric (0.50323 eV) than anti-symmetric (0.51188 eV) orbitals, suggesting that symmetric interaction is better. This hypothesis is later confirmed by the transition state MO analysis (see later).

Transition State

Guess geometry for TS

The transition state of the reaction was located with the Berny algorithm using the AM1 method. The starting guess geometry was created by combining the AM1-optimised geometries of 2 and 3, with the terminal carbons of 2 and 3 spaced 1.9 Å apart. Upon optimisation, the transition state geometry was then further optimised at the HF/3-21G level.

Transition State Optimisation

Method	Eelec / Hartrees	νimag / cm-1	rC2-C3 / Å
AM1 (SPECTRa)	0.11166	-956	2.12
HF/3-21G (SPECTRa)	-231.60321	-818	2.21

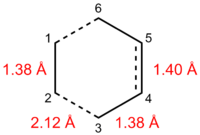
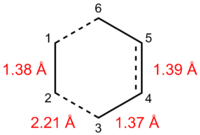
The Van der Waals radius of carbon is 1.70 Å, a typical C=C double bond is normally 1.34 Å in length, while C-C single bonds vary from 1.47-1.53 Å depending on the environment:

• -C-C-: 1.53 Å
• =C-C-: 1.50 Å
• =C-C=: 1.47 Å

The existing C-C bonds in the transition state all have lengths typical of C=C bonds, suggesting that the double bonds in butadiene and ethene largely maintain their character in the transition state. Furthermore, the C-C bond being formed in the Diels-Alder reaction has a length of 2.1-2.2 Å in the transition state, indicating that the new bond is far from being formed in the transition state structure. Nevertheless, the C2-C3 distance is less than twice the Van der Waals radius of carbon, implying partial bonding between C2 and C3 in the transition state. On the whole, this points to a relatively early transition state, implying that the transition state is closer in structure to reactants than products.

The higher level HF/3-21G calculations give a longer C2-C3 distance than for the lower-level AM1 calculations; additionally, the C3-C4 and C4-C5 bond lengths are both lower with HF/3-21G. This suggests that HF/3-21G models an even later transition state than AM1, and implies that AM1 possibly overestimates the attractive interactions between the ethene and butadiene frontier MOs.

AM1		HF/3-21G
	Vibration		Vibration

The imaginary vibrational frequency of the transition state corresponds to the forward and backward direction of the reaction coordinate, with synchronous formation or breaking of the C2-C3 and C5-C6 bonds. In contrast, the lowest positive frequency corresponds to an asynchronous twisting of the ethene fragment with respect to the butadiene fragment.

Frontier molecular orbitals of transition state

Method		HOMO	LUMO
AM1	MO
	Symmetry	a	s
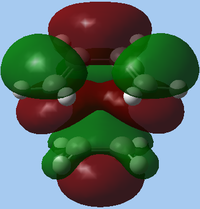
HF/3-21G	MO
	Symmetry	s	s

In this case, the HOMO of the transition state is dependent on calculation method; it is found that the HOMO and HOMO-1 are swapped in terms of relative energies, when switching from AM1 to HF/3-21G. In the case of the AM1 HOMO, the asymmetric nature of the HOMO implies that asymmetric frontier MOs were used to form this, namely the HOMO of butadiene 3 and LUMO of ethene 2. Alternatively, considering the HF-3-21G calculation, the HOMO is found to be symmetric about the vertical plane of symmetry, and must therefore be formed from the symmetric HOMO of ethene 2 and LUMO of butadiene 3.

This reaction is therefore allowed by symmetry, as the frontier MOs are of the right phase and symmetry to react. However, the energetics of the reaction govern its favourability - substituent effects modify the HOMO and LUMO energy levels of the diene and dienophile and may therefore influence the energetic compatibility of overlap, favouring or retarding the reaction. This leads on to the next section, where these substituent effects are investigated.

Cyclohexa-1,3-diene and Maleic Anhydride

Introduction

Although the reaction between butadiene 3 and ethene 4 is the simplest conceivable Diels-Alder reaction, it does not work well in practice because the dienophile 4 is not conjugated to any electron-withdrawing groups (EWGs) and has a high-energy LUMO, disfavouring its interaction with the HOMO of the diene 4.

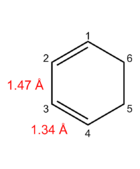
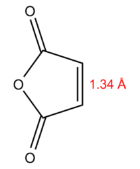
Of the many dienophiles that have been employed successfully, maleic anhydride 6 is among the most common. Its twin carboxylic acid groups effectively withdraw electron density from the alkene, lowering the energy of the LUMO. This may be rationalised as follows: any electron density added to the LUMO will be withdrawn inductively by the EWGs, reducing their destabilising effect (as the LUMO is anti-bonding) on the molecule, as compared to an unsubstituted alkene that similarly accepts electron density into its LUMO. Consequently, Diels-Alder reactions with maleic anhydride 6 are extremely facile. The use of cyclohexadiene 5 further increases the rate of reaction, as the diene is forced into an s-cis conformation by the ring, and is therefore always in the right conformation for reaction - contrast this to butadiene 3, which may take on the unreactive s-trans conformation.

Reactants and Products

Reactants 5 and 6 were first optimised with HF/3-21G prior to use in the transition state search algorithms. These were further optimised by B3LYP/6-31G(d) in preparation for comparison with transition state energies, also calculated at the B3LYP/6-31G(d) level, to calculate activation barriers. The results are tabulated below:

Reactant and product optimisation, B3LYP/6-31G(d)

Molecule	Eelec / Hartrees	Low frequencies						Lowest normal freq.
Cyclohexadiene 5	-233.41893	0	0	0	14	16	19	191
Maleic anhydride 6	-379.28954	-11	-8	0	0	2	11	168
Endo product 7a	-612.75829	-20	-12	0	0	0	10	57
Exo product 7b	-612.75579	-13	-1	0	0	0	17	65

Cyclohexa-1,3-diene 5	Maleic anhydride 6

Intrinsic Reaction Coordinates

IRC calculations were performed at the HF/3-21G level, with force constants calculated at each step, and show in detail the energy changes in the system through the course of the reaction (energy changes are not comparable due to the different level of theory).

For both reactions, a gradual path takes the system up the potential energy surface towards the TS, whereupon it immediately travels down a steep slope to the low-energy products. The endo TS is observed to be lower in energy than the exo TS, while the endo product 7a is slightly more stable than the exo product 7b.

IRC plots

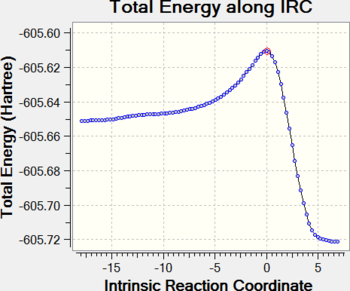
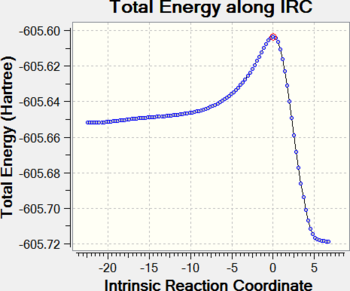
Endo IRC	Exo IRC

Transition State

Transition states were located with the QST2 (endo) and QST3 (exo) methods, as the Berny algorithm failed to locate both transition states, instead arriving at a structure with puckered cyclohexa-1,3-diene. For the exo transition state, the QST2 method also failed to arrive at a transition state; switching to the QST3 method by including a guess structure aided the algorithm in locating this geometry.

Optimised structures for cyclohexa-1,3-diene 5 and maleic anhydride 6 were used for reactant guess geometries, while optimised structures for endo and exo products were used for product guess geometries. For the QST3 method used for the exo transition state, a guess transition state was generated by decreasing the yet-unformed C-C bond distance to 2.3 Å, from the 2.8 Å in the reactant guess geometry.

TS optimisations were performed first at the HF/3-21G level, and once located, were further optimised with the Berny algorithm using B3LYP/6-31G(d), as secondary orbital interactions are better modelled with the inclusion of diffuse orbitals in the 6-31G(d) basis set.

Transition State Optimisation

Method	Endo			Exo
	Structure	Eelec / Hartrees	νimag / cm-1	Structure	Eelec / Hartrees	νimag / cm-1
HF/3-21G	Jmol / SPECTRa	-605.61037	-644	Jmol / SPECTRa	-605.60359	-647
B3LYP/6-31G(d)	Jmol / SPECTRa	-612.68340	-447	Jmol / SPECTRa	-612.67931	-449

Endo, B3LYP/6-31G(d)		Exo, B3LYP/6-31G(d)
	Vibration		Vibration

Structurally, the endo and exo transition states have the same carbon skeleton and connectivity, differing minimally only in the orientation of the anhydride group, with endo form having the anhydride group eclipsing the alkene group (-CH=CH-), and the exo form having the anhydride group eclipsing the alkane group (-CH₂-CH₂-). Consequently, the exo form is likely more strained due to repulsive van der Waals interactions between the anhydride group and the CH protons of the bicyclic ring bridge.

From the bond distances in the endo and exo transition states, it can be seen that σ_C-C bond formation is more advanced in the endo transition state, an observation that may be attributed lesser steric repulsion and attractive secondary orbital interactions resulting in stabilisation of the endo transition state; as the reaction is exergonic overall, this would give rise to a later transition state with more advanced bond formation.

Comparing the transition state with reactant geometries, the extent of bond formation becomes clear, with the C1-C2 and C3-C4 C=C bonds in 5 as well as that in 6 lengthening, while the C2-C3 bond in 5 shortens and takes on more double bond character, just as the two new σ bonds begin to form. Overall, the transition state demonstrates synchronous bond-formation and bond-breaking, consistent with a pericylic reaction.

Energetics

The energies, enthalpies and free energies (298 K) of all species involved in the reaction are tabulated below:

Energies, enthalpies and free energies, 6-31G(d)

Molecule	Eelec / Hartrees	Eelec + ZPE / Hartrees	Eelec + therm + ZPE / Hartrees	H / Hartrees	G / Hartrees
Cyclohexadiene 5	-233.41893	-233.29610	-233.29093	-233.28999	-233.32370
Maleic anhydride 6	-379.28954	-379.23366	-379.22847	-379.22753	-379.26273
Endo TS	-612.75579	-612.50214	-612.49179	-612.49084	-612.53833
Exo TS	-612.67931	-612.49801	-612.48766	-612.48672	-612.53426
Endo product 7a	-612.75829	-612.57207	-612.56260	-612.56166	-612.607177
Exo product 7b	-612.75579	-612.56938	-612.55998	-612.55903	-612.60428

From this data, the energy changes and activation energies (298 K) involved in each reaction were calculated, as shown below. The associated entropy changes were then calculated (ΔS = (ΔH - ΔG) / T) from the free energies and enthalpies.

Energy changes and activation energies, kJ mol^-1; entropies, kJ K^-1 mol^-1; 6-31G(d)

Reaction pathway	ΔE	ΔE‡	ΔH	ΔH‡	ΔG	ΔG‡	ΔS	ΔS‡
Endo	-113.4	72.5	-115.9	70.0	-54.5	126.3	-0.206	-0.189
Exo	-106.5	83.3	-109.0	80.9	-46.9	137.0	-0.208	-0.188

The calculated energies bear out the hypothesis that the exo transition state is more strained than the endo form, with the activation energy, enthalpy and free energy all having a higher barrier for the exo TS. This strain is also reflected in the overall reaction energy changes, as would be expected from the fact that the products 5 are structurally similar to the transition states and therefore experience the same kinds of steric interactions.

The overall reaction is thermodynamically favourable, involving a release of energy, whether measured by energy, enthalpy or free energy. This is due to the increased stability of the adducts 7 as compared to the reactants 5 and 6, which may be further explained by the fact that the Diels-Alder reaction converts 2 π_C-C bonds into 2 relatively stronger σ_C-C bonds.

The difference between ΔE and ΔH is a constant 2.5 kJ mol^-1 throughout, as the two quantities differ only by RT (T = 298 K). The calculated ΔG values differ significantly from ΔE and ΔH due to the effect of entropy - with the diene 5 and dienophile 6 combining to form a single adduct 5, the order in the system increases, corresponding to a decrease in reaction entropy. As a result, ΔG and ΔG^‡ become more positive because the enthalpic contribution of bonding is offset by the entropic penalty of combining two separate molecules into one.

The associated entropy changes are similar for both endo and exo pathways, indicating that at this level of theory at least, the bonding (enthalpic) contributions of the secondary orbital overlap are much more significant than its entropic effects. Nevertheless, the entropy change from reactant to transition state is slightly more negative for the endo pathway, which may be understood from the decreased flexibility afforded to the TS by the secondary orbital interactions, which require the diene and dienophile to align in a specific manner.

Molecular Orbital Analysis

An examination of the filled molecular orbitals was performed to probe for the presence of any orbital overlap between the diene and dienophile that might explain the secondary orbital interactions postulated.

Examining the HOMO of both endo and exo transition states, no significant interactions exist between the anhydride fragment and the rest of the system. Only upon decreasing the isovalue cutoff to 0.005 is any overlapping interaction observed - with the endo TS, the central O atom is of the right symmetry for π-overlap with the HOMO of the diene, but the two carbonyl O atoms are anti-bonding with respect to this diene HOMO; conversely, with the exo TS, the opposite is true, with the carbonyl O atoms exhibiting some bonding interaction with the diene.

Endo, HOMO	Exo, HOMO

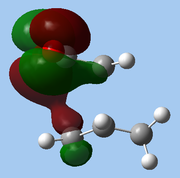
The lower-lying molecular orbitals were then examined for secondary orbital interactions. Of these, it was noted that HOMO-4 of the endo TS showed significant overlap between the anhydride's central O atom and the diene. This provides support for the hypothesis that secondary orbital effects account for the endo selectivity of Diels-Alder reactions: with the stabilising bonding interaction, the energy of the endo TS is lowered, reducing the activation barrier for the reaction pathway leading to the endo adduct, hence favouring this product kinetically.

Endo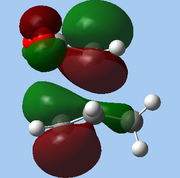
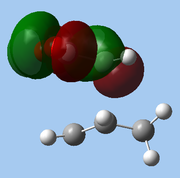
	HOMO-1	HOMO-2	HOMO-3	HOMO-4
Exo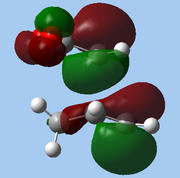
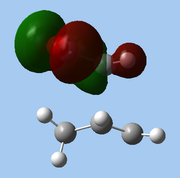
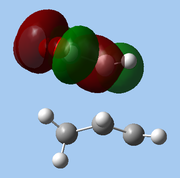
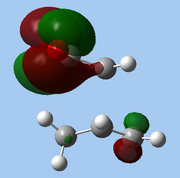
	HOMO-1	HOMO-2	HOMO-3	HOMO-4

Solvent Effects

Aside from the secondary orbital interaction effects considered so far, the solvent is also known to exert an influence on the rate of Diels-Alder reactions as well as on endo/exo selectivity, due to the large dipole moment of the transition states, which may be stabilised by solvent interactions; with protic solvents, hydrophobic effects or hydrogen-bonding interactions with carbonyl-substituted reactants can also stabilise the transition states and accelerate reaction rates.

As modelling hydrogen-bonding interactions require the inclusion of explicit solvent molecules, which rapidly increases computational cost, solvent effects are investigated here for aprotic non-coordinating solvents only. As the endo TS was observed to have a much larger dipole moment (6.11 D) than the exo TS (5.55 D) in the gas-phase, switching to increasingly polar solvents is expected to stabilise the endo TS to a greater extent, favouring the endo product kinetically.

All reactant, product and TS geometries were optimised at the same level of theory, 6-31G(d), using the same parameters with an added solvent continuum reaction field (SCRF) modelled with the polarisable conductor calculation model (CPCM). Three non-coordinating solvents of increasing polarity, benzene (0.00 D), dichloromethane (1.60 D) and acetonitrile (3.92 D) were used for comparison with the gas-phase calculations; the results are tabulated below:

Free energy changes and activation energies, 6-31G(d), kJ mol-1

Reaction pathway	Gas-phase		Benzene		Dichloromethane		Acetonitrile
	ΔG	ΔG‡	ΔG	ΔG‡	ΔG	ΔG‡	ΔG	ΔG‡
Endo	-54.5	126.3	-53.6	123.7	-53.2	121.3	-53.0	120.6
Exo	-46.9	137.0	-45.0	136.5	-43.6	135.5	-43.3	135.2
exp(Endo/Exo)		2.51		2.47		2.45		2.44

As expected, the transition states are calculated to be relatively stabilised by solvent, as compared to the reactants, reducing the activation energy barrier for the reaction, with the most polar solvent (acetonitrile) having the greatest effect, while the gas-phase reaction has the highest activation energy barrier.

Assuming a simple Arrhenius model for rate of reaction and a constant pre-exponential factor, the endo/exo ratio would be given by exp(ΔG^‡_endo / ΔG^‡_exo). However, in this case, the calculations do not provide evidence for increasing endo selectivity with increasing solvent polarity, and instead predict the opposite trend, with the exo product being kinetically favoured by polar solvents. This suggests that the assumption of the same pre-exponential factor for both endo and exo pathways might be an oversimplification, or that the level of theory or solvent model are not accurate enough to model the solvent effects. In any case, the experimentally observed solvent effects similarly minor, and the differences in calculated selectivity ratios are small and possibly within experimental and calculation error.

Conclusion

In conclusion, transition states for two Diels-Alder reactions were found using a variety of methods: the Berny algorithm, QST2, and QST3. By optimising the reactants and products at the same level of theory, 6-31G(d), reaction energy changes and activation energies were calculated, and the endo product found to be both kinetically and thermodynamically favoured in the gas-phase. This was attributed to enthalpic factors, which were rationalised by secondary orbital effects elucidated by examining the filled molecular orbitals of both endo and exo transition states. Although solvent effects were predicted to affect both reaction rates and endo selectivity, calculations at the 6-31G(d) level with a continuum solvent field (CPCM) only revealed an effect on reaction rates, with negligible effects on selectivity.