Rep:Mod3:yz908

Computational Chemistry Course-Physical Analysis

Introduction

In physical chemistry, the macroscopic, atomic states are analysed during chemical reactions using theoretical background and phycial concepts. It is a study of molecular motion, thermodynamics, quantum mechanics and the statistical chemistry. The idea is predominantly a macroscopic science, using corresponding principles that are related to the molecular geometry and orientations. Equilibrium are investigated, which will lead to the effect of intermolecular forces on materials, reaction kinetics and electrical conductivity, surface chemistry.

In this course, the concept of computational methods are brought about to the physcial experiments. This is to characterise molecular geometries in transition state, and to calculate the potential energy surface for a best suitable states. Previously, potential energy surface models have been studied for dynamic calculations in order to discover the transition state. Here, several computational methods are discussed, the total energy is calculated with optimised structures. To fully investigate the transition structures, molecules of large sizes are used, force field is then applied to define the best suitable geometries. It it then become possible to determine the bond breaking and bond forming changes. The MO theory come into large uses as well, by applying the Schrodinger equation, the potential energy surface could be analysed and studied on the overlap and molecular orbital interactions. Activation energy and barrier high could therefore be identified.

The transition state is a state, which can not be isolated, different from intermediate state. In this experiment, computational methods could be used for Diels-Alder cycloaddition calculations. Another example, [3,3] sigmatropic shift are discussed here for its concerted reaction process. It is then seen that the Gaussian calculations are susceptible in reactivity studies. It therefore allows the determination of reaction mechanism and characterisation for proving the theories.

Basis Set in the Calculations

ChemBio3D are diversely used for computational analysis to obtain the optimised geometry. Here, transition states of various molecular structures are investigated, and ChemBio3D force field are not sufficient enough for calculations. This is due to the lack of details linking bond formation and bond breaking, regarding the electronic interactions. During chemical reactions, electron distribution has a huge effect in determining the geometry. Therefore, MO theory is applied, Schrodinger equations are solved to proceed the transition state analysis. The basis set used here is found to be Hartree-Fock Calculations and 3-21G, B3LYP/6-31G. The Cope rearrangement of 1,5-hexadiene, low-energy and transition geometries of 1,5-hexadiene were located in order to determine reaction mechanism. [3,3]-sigmatropic shift are here also to identify the "chair" or "boat" transition structure, "boat" is considered to be higher in energy.

Cope Rearrangement of 1,5-Hexadiene

The Cope rearrangement of 1,5-Hexadiene can be classified into the [3,3] pericyclic reaction. It's a sigmatropic reaction, which includes the migration of σ-bond around the chain from one end of the molecule to the other while a concerted fashion. This has been the centre of research and focus both in practical experiments and computational analysis. Here, computational method with Gaussian B3LYP calculation has been widely used for optimisation of best structures. Following is the mechanism and reaction scheme for the 1,5-Hexadiene rearangement reaction:

This reaction satisfy the Huckle rule of 4N+2 electrons involved. There are 6 electron in total in this pericyclic reaction. When heat is provided, Huckle process is undertaken with suprafacial rearrangment. This reaction is believed to be in a concerted fashion, the machanism is shown obover with no intermediate involved, only a transition state where 6 electrons are moving at the same time, the bonds forming and breaking are at the same time. Transition state seen are either in a boat or chair structure.. In order to study the transition state, the lowest comformation energy is identified and the boat conformation is believed to be in a higher energy state than the chair conformation. This is done by first optimising reactants and products during the pericyclic mechanism.

Optimisation of the reactants and products

The 1,5 hexadiene has a structure with two C=C double bonds at both ends of the molecule. By analysing the chain, a single bond is appearing in the middle of the molecule. This is the reason why 1,5 hexadiene has a free rotation around the single bond. With GaussView 5, the reactant molecule was drawn in anti and gauche conformations. The Gauche conformation is however regarded to be the one with higher energy. 3-21G Basis Set calculation was then run for the cleaned molecule and total energies are summarized later in the report.

First of all, the anti conformation is optimised in the programme and is seen to be the most stable structure with the lowest energy. Secondly, the Gauche conformation is drawn and optimised using the same methods. The total energy is then found to be slightly higher than the anti conformation. This is then proved to be different from the literature. From the previous report, Gauche conformation was determined to be with lower energy. This is due to a better geometry with electron cloud optimisation, therefore orbital effect is taken into account for the final results. .

Optimisation of Anti Conformation

The molecule of 1,5-hexadiene is drawn out in the GaussView Programme in an anti conformation, all the bonds between carbon atoms are made in an antiperiplanar geometry. Hydrogens are added and the structure is then adjusted to allow a flecible space using the 'Clean' function under 'edit' and 'result'. Optimisation of this conformation was then carried out using best suitable basis set with 3-21G. Results are obtained as follows:

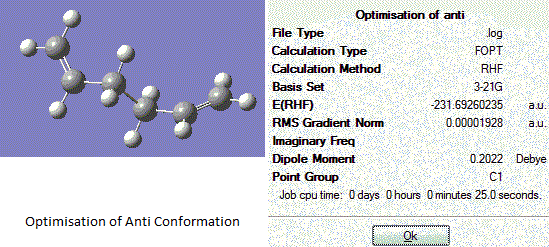
Anti Conformation

The log file of the optimisation analysis for anti conformation is here: Output log file

When the anti conformation is optimised, the 'summary' button in the results session of the menu is clicked and the symmetry point group for this structure is found to be Ci. Minimum total energy is found to be -231.692602 a. u. After comparison with the Appendix 1, this geometry optimisation creates a molecule corresponding to anti-2 conformation.

Optimisation of Gauche Conformation

By adjusting the geometry of the starting molecule, the molecule of 1,5-hexadiene is drawn out in the GaussView Programme in an gauche conformation. all the bonds between carbon atoms are made in an gauche conformation. Hydrogens are added and the structure is then adjusted to allow a flexible space using the 'Clean' function under 'edit' and 'result'. Optimisation of this conformation was then carried out using best suitable basis set with 3-21G. Results are obtained as follows:

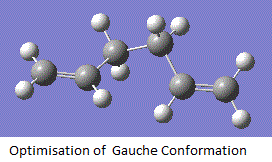
Anti Conformation

After the gauche conformation is optimised, the 'summary' button in the results session of the menu is clicked and the symmetry point group for this structure is found to be C₁. From here, the anti conformation is believe to have a lower energy than the gauche conformation. This is due to the large steric hindrance around the gauche conformation. However, after computational calculation, with a minimum total energy to be -231.69270 a. u. This gives a 0.320 kJmol^-1 energy lower than the anti conformation. This phenominum attributes to the stabilisation of the electronic interaction between the double bond orbital and the hydrogen orbital adjacent to it. After comparison with Appendix 1, it matches with the Gauche-3 structure.

The log file of the optimisation analysis for gauche conformation is here: Output log file

Lowest Energy Conformation

To fully study the transition state associated with activation barrie and the thermodynamics of the molecule, conformation with the most stable geometry is studied and identified. Therefore, other anti conformers and gauche conformers in Appendix are analysed and their properties including point groups are summarised below:

conformation	Images	Energy /a.u	Energy /kJ mol-1	Name	Symmetry Group
Gauche		-213.69172	+2.21	Gauche-2	C2
Gauche		-231.68958	+7.56	Gauche-5	C1
Gauche		-231.69253	0.00	Gauche-3	C1
Anti		-231.68910	+9.11	Anti-3	C2h
Anti		-231.69096	+4.33	Anti-4	C1
Anti		-231.69249	+0.30	Anti-2	Ci

According to the table above, the gauche-3 geometry is found to be the one with lowest energy, therefore most stable. It is believed that the anti conformation is the most stable structure due to the least steric hindrance effect. The reason for Gauche conformation to be most stable is explained by also the electronic effect.

Energy of Anti-2 Conformer

The anti-2 conformer has been optimized in part d as shown in Table 1. The energy of the conformer is found to be -231.69249 a. u. This is the lowest energy structure found using computational methods. In theory, the energy is obtained as -231.69254. Based on the fact that the computaional result is in a good agreement with the literature, the structure will be applied for further calculations.

Optimisation of Anti-2 by B3LYP

Previously 3-21G was used as the basis set to perform optimisation. This methos does not cost a lot, however it is relatively inefficient in calculation for the minimum energy. Therefore, a better calculation basis set is applied as B3LYP, which is better in calculating larger size of atoms. Symmetry group is identifies as Ci.

After second optimisation, the total energy is identified as -234.6120 a.u. By compareing both energies gained from 3-21G and B3LYP, it is shown that B3LYP brings a more stable structure. Due to the difference in the nature of calculation method, the structure can not be simply compared. Other tools such as the dihedral angles, bond length are compred as well to obtain a better explanation of the reason behind this matter:

Basis set	C=C length /Å	Bond length of single bonds/ Å	Bond length middle single bonds /Å	Dihedral angle LHS bonds /o	Dihedral angle middle bonds /o	Dihedral angle RHS bonds /o
HF/3-21G	1.34	1.51	1.57	115.6	180.0	115.6
B3LYP/6-31G(d)	1.35	1.49	1.57	119.0	180.0	119.0

From the comparison results, there is not a large variation between the two optimisations apart from the dihedral angles and the bond length. Generally, the second optimisation with B3LYP produces a large bond angle and length, so minimise the steric hindrance effect. In theory, the C-C and C=C bond length is 1.53Å and 1.35Å respectively. The two optimisations through different methods do contain small variation between them. In terms of bond lengths, the B3LYP gives results closer to the literature. Therefore, it is clearly shown that the computational results are in a good agreement with the experimental and literature values.

Frequency Analysis of Anti-2 Conformer

To further compare the results, frequency analysis is carried out. This is to comfirm the geometry we obtained is a energy minimum. When the vibrational frequencies show positive results, this conformation is the lowest in energy. However, if it is negative, the structure would be in its transition state. IR Results and comparison are shown below:

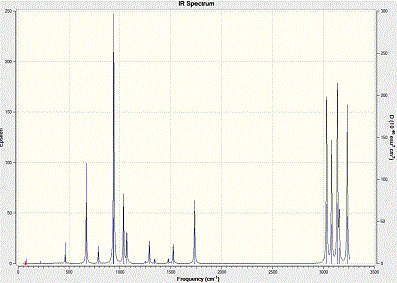
At zero temperature, the sum of electronic and zero-point energies is the potential energy, which is indicated by the following equation E1 = Eelec + ZPE. At room temperature pressure, the contribution comes from translational, rotational and vibrational energy, which is again seen as the equation E2 = E1 + Evib + Erot + Etrans. From thermodynamics, the sum of electronic and thermal free energies is shown below: G = H - TS.

Optimisation of the “Chair” and “Boat” structures

1, 5 hexadiene molecule can perform Cope Rearrangement either through a chair or a boat transition state. The "chair" and "boat" transition structures for the Cope rearrangement were created in this exercise. In this experiment, the transition states are studied.

Optimisation of Chair Allyl Fragment

For the chair transition state, the ally fragments were optimised. Results are shown below:

The minimum energy is seen to be 115.811 Hartree.

Optimisation of the Chair TS(Berny)

This fragment was then copied twice in to a new MolGroup, in the chair transition state, the terminal carbons of molecule to be 2Å in terms of bond length. This is carried out using optimisation and frequency calculation using TS(Berny)using 3-21G basis set.

The energy of the optimised transition state has a negetive value of -231.620 Hartree and shows a negative vibrations of -817.955cm-1 with bond lengths of 2.0195Å and 2.0201Å.

These all show a great agreement with the literature value in theory.

Optimization of Chair TS using Hessian Method

The structure are manipulated manually so that it reflects the shape of the chair conformation. Hessian calculation was then used to perform the best calculation with the basis set of 3-21G. The optimization and frequency were carried out. The TS Berny was achieved. Results and structure are shown below:

Transition State is believed to have an energy of -231.61932 a.u, which is higher than the anti-2 starting material. This indicates that the chair conformation gives a higher transition state. The energy barrier increases. By frequency analysis, the values are seen as negative at 820cm^-1, for the potential energy surface. This observation shows that the two ends of the whole chain was moving together, and the new bonds are forming during the processes. Steric hindrance are considered and optimised during the process to achieve a best stabilisation from the analysis.

Optimization of the Chair Frozen Coordinate Method

Frozen Coordinate Method was also used here to perform the calculation for the transition state. As the name suggest, the terminal carbon atoms are are frozen to be kept still during the optimisation method. This is performed by inserting Opt=ModRedundant. After this has been carried out, the molecule is not frozen. This is done by minimising the cost for computational method calculations. Since the bond length was set to be 2Å, the structure is optimised and results are shown below:

Following results have shown the comparison between the results generated from the Frozen Coordinate Method and the previous methods:

basis set	TS (Berny)	frozen coordinate method
Energy /a.u	-231.69311	-231.69311
C-C Bond formation length /Å	2.00	2.00
C-C Bond breaking length /Å	2.01	2.01
Imaginary Frequency /cm-1	-817.89	-818.10

The total energy is the same and hasn't been changed. This is also the case for the bonding formation and breaking processes. There is only slight differences between the frenquencies. Therefore, this method is better in terms of gaining a more accurate results. However, every method is not perfect. There are both advanteges and limitations to a certain extent. The Frozen Coordinate Method although uses longer time in terms of calculation steps, but it gives more accurate results and more professional processes. Therefore, the results are more realiable.

Optimization of Boat Conformation

When the chair optimisation is carried out, the boat conformation is optimised using QST2 method. This is started by inserting coordinates and modelling the starting materials. With this calculation, the reactants and products wre used, calculations are done between them to find the transition state.

The results show that the transition state is similar to the chair transition state.

To obtain the best performance over optimisation calculations, the angle between allyl fragments was substituted by 0^o. The structure is calculated using 3-21G, the boat conformation is received. Boat conformation shows a lowest energy of -231.6030 a.u, which is in a higher energy level than the chair conformation -231.6189 a.u. Frequency was shown to be negative 839 cm^-1, which is lower than thay of the chair structure, negative 820 cm^-1. Therefore, the transition state is gained. Hence, the energy change in bond formation and breaking processes are higher in the boat transition state than that of the chair conformation. Bond length and angle is bigger in boat transition geometry. These arttribute to the steric hindrance effect of boat transition state.

Intrinsic Reaction Coordination

Intrinsic Reaction Coordinate calculation proceeds through the lowest energy pathway for the transition state. It is applied to the chair transition state via Berny method to give the best conformation. Because of this symmetry of the molecule and reaction coordinate, the intrinsic reaction coordinate calculation uses 50 points.

IRC was then applied by a larger number of points, until it eventually reach the optimisation structure. Force constants are calculated along the process. The IRC is a very useful tool to reach the local energy minimum after calculations from the transition states. Results are obtained below:

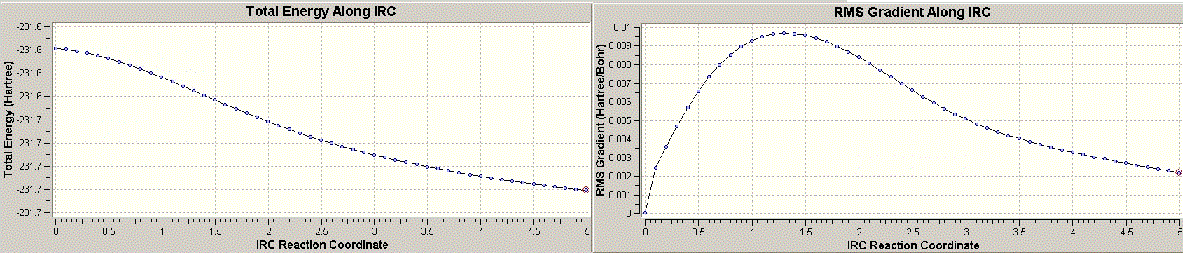
According to the results, it is identified that as the plateau has been reached, the calculation is thought to reach the end. The RMS does not reach zero. Minimum energy reached here is -231.6890 a.u with a symmetry group of C₂. Due to the appearance of the frequency value, the structure is believed to have not reached the minimum energy state.

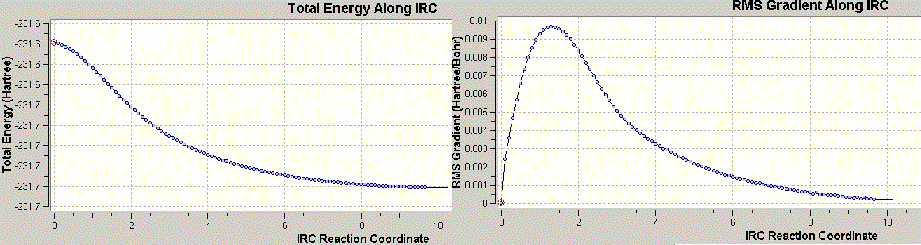
Method is applied once more and the force constant was used in the calculation at all stages of the calculation. This approach has been considered to be more costy but is yielding more accurate results.

Here there is no frequency found and the process is believed to be producing the energy minimum. The graph is reaching zero. Hence the energy is achieving -231.6899, much lower in energy than the first calculation with a symmetry group of the C₂. Therefore, from this point group, it is seen that the chair transition state is leading the product of Gauche-2 conformation.

Activation Energy Analysis

For activation energy, the boat and chair conformations are optimised with B3LYP, and the frequency analysis is then followed under standard temperature and pressure. Results are shown below:

basis set	3-21G	3-21G	3-21G	B3LYP	B3LYP	B3LYP
energy/a.u	Electronic energy	electronic + zero-point energies 0K	electronic + thermial energies at 298.15K	Electronic energy	electronic + zero-point energies at 0K	electronic + thermial energies at 298.15K
Chair Transition State	-231.6190	-231.4659	-231.4615	-234.557	-234.415	-234.4089
Boat Transition state	-231.6025	-231.4502	-231.4449	-234.5429	-234.40185	-234.3959
Anti-2	-231.69249	-231.53949	-231.53245	-234.61169	-234.46917	-234.46179

The geometry produced by 3-21G and B3LYP are quite the same to each other. However, the minimum total energy are of slightly different. Since B3LYP is a more precise and accurate calculation method, it is obtaining better results. The activation barrier could then be gained by considering the following equation: E_a = electronic + zero-point energies of transition state. Results from calculation are shown below:

basis set	3-21G	3-21G	B3LYP	B3LYP	Experimental values
Temperature used	0	298.15	0	298.15	0
energy difference in chair /kcal mol-1	45.6	44.7	34.1	32.9	33.4+0.4
energy difference in boat/kcal mol-1	55.9	55.0	41.9	40.9	44.6+2.0

Therefore, it is seen that the boat conformation and transition state is generally in a higher energy state than the chair conformation. This is mainly due to the more stable chair conformation has a lower steric hindrance effect. Results obtained from the B3LYP method are much similar to the ones reached by 3-21G. In conclusion, computational methods are seen as very efficient tools in determining the lowest energy conformation and predicting the products for a certain reaction. Although, as the basis set used gets more efficient, the relative costs increase. However, computational chemistry are still seen as a focus of current research techniques.

Analysis of Diels Alder Cycloaddition

Cyclopentadiene has molecular formula C5H6. It has a uncomfortable odor and often appears as a colourless liquid. Normally, cyclopentadiene dimerizes in air at room temperature and pressure. This results in the formation of dicyclopentadiene undergoing a Diels-Alder reaction. The process is reversible. However, if treated under heat, the dimer will soon break into its original monomers. Under low temperature conditions (generally approx -20°C), the monomer could be stored for several days if no other reactions.

Cyclopentadiene dimerizes through a [_π4+_π2] cycloaddition reaction. This reaction then gives 2 different products, which are stereoisomers of each other. There are either endo- or exo-product.

Dials Alder reaction is known as a famous cycloaddition reaction. During the process, diene approaches dieniphile in a concerted fashion to form a cyclo product. It is also a [4π + 2π ] process when we are describing the number of electrons involved in the process.

In this experiment, the cycloaddition reaction of butadiene and ethylene are analysed. This pericylclic reaction involves the formation of new sigma-bonds, and the breakage of the pi-bonds of diene at the same time. The HOMO-LUMO electrons are seen to have the same phase to allow the reaction.

Optimisation of Butadiene and Ethylene

In the reaction of butadiene and ethylene, the diene approaches dienophile from either below or above the place of the molecule. This is an example of the Diels Alder cycloaddition reaction. Diene is the Butadiene molecule and dienophile is the ethylene molecule. The reaction happens due to the interaction of in-phase pi-orbitals, which causes the bond formation of two new σ-bonds. This is a [4π + 2π ] process.

In GaussView programme, the molecule of butadiene and ethylene is drawn and studied under optimization with MO theory. By analysing the molecular orbitals and the relative symmetry. The reaction mechanism and process could be determined. Results are shown below:

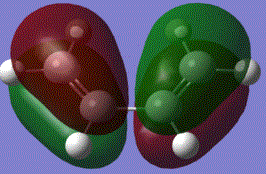
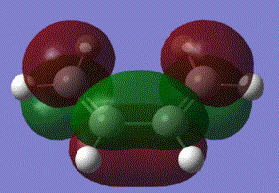
It can be shown that in the reaction, HOMO of ethylene and LUMO of cis butadiene overlap, and the LUMO of ethylene and HOMO of cis-butadiene also overlap to produce the following effect:

Type	butadiene HOMO	butadiene LUMO	ethylene HOMO	ethylene LUMO
MO Shape
MO Symmetry	Anti-Symmetric	Symmetric	Symmetric	Anti-Symmetric
MO Energy/ a.u	-0.34379	+0.01706	+0.05279	-0.38769
Total energy /a.u	0.04880	N/A	0.02620	N/A

From the table above, the symmetry of the molecular orbitals can be determined and studied. It is identified that the HOMO of butadiene HOMO is in the same symmetry as the ethylene LUMO and butadiene LUMO is in the same symmetry as the ethylene HOMO. Based on the orbital theory, the orbitals can only interact or overlap if they have the same symmetry and similar energy level. Therefore, the butadiene HOMO will be available for reaction with the ethylene LUMO, and the butadiene LUMO with the ethylene HOMO. According to the total energy od the molecular orbitals, it is seen that the ethylene LUMO is at a lower energy than the butadiene HOMO. Electrons will then be donated from the higher butadiene HOMO into the lower ethylene LUMO.

Optimisation of Transition State

The optimisation of transition state of this reaction is studied by modelling the diene and diemophile structures. QST2 can be used to model the transition state from the reactants and products. Berny can be applied by producing the fragments. However, QST2 costs time but produces reasonable results. Bond length is thought to be 2Å first. Another method based on AM1 was applied to optimise with B3LYP basis set, the results are shown as follows:

	AM1	B3LYP
Frequency/ cm-1	-960	-530
Bond formation	2.11 Å	2.25 Å
Energy/ a.u.	234.11159	-234.5440

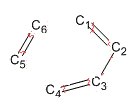
bond type /Å	Starting	Ending
C1-C6 new bond	2	2.10
C4-C5 new bond	2	2.10
C1=C2	1.35	1.39
C2-C3	1.48	1.42
C3=C4	1.35	1.39
C5=C6	1.32	1.39

With the B3LYP approach, newly formed bond length is longer than the ones obtained by AM1. Due to the difference in calculation methods, the results obtained may vary. sp3 is usually 1.55 Å in bond length with 1.35 Å for sp2. The Van der Waals radius of carbon is found to be 1.70Å. The 2Å bond length is longer than carbon to carbon single bond but smaller than twice of the van der waals radii. Therefore, it shows an orbital interaction during the bond formation process. These all occur in a concerted reaction. The anti-symmetric butadiene HOMO interacts with the anti-symmetric ethylene LUMO, transition state attributes to the overlap of symmetric ethylene HOMO with the butadiene LUMO.

From the analysis, the distance between C₁-C₆ and C₄-C₅ reduces as it approaches the transition state. The bond length between C=C bond increases during the bond breaking process so that the C=C bond is breaking to form the single bond.

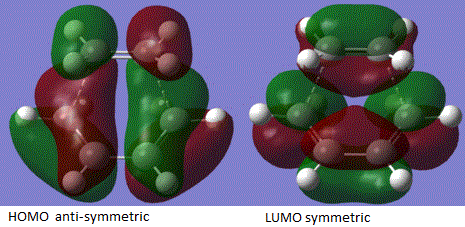
The molecular orbital analysis is shown above and the energy of MOs at the transition state was shown by applying the equation E_LUMO – E_HOMO. Therefore the interaction between butadiene HOMO and the ethylene LUMO can be shown as 0.397 a.u and that of butadiene LUMO with ethylene HOMO is shown to be 0.406 a.u. This is the reason why the in energy tems, the reaction is preferred and stabilised after the interaction.

Region-selectivity of Diels Alder Reaction

Cyclohexa-1,3-diene reacts with maleic anhydride through a Diels Alder reaction with stereochemistry to produce the endo-conformer over the exo-conformer. This is mainly due to the kinetic condition in which the reaction undergoes.. When the reaction is in kinetic control, the endo product will form via a lower energy transition state. On the other hand, when the reaction is under thermodynamic control, it would undergo a higher energy transition state but form a more stable product. Therefore, the 3-21G basis set is used and the transition structure is studied using TS Berny approach.

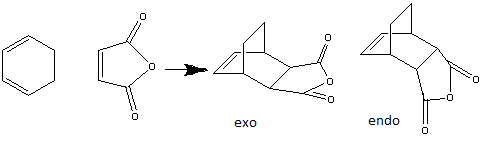
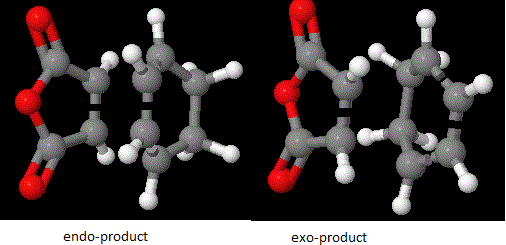
Molecule:exo product	Molecule:endo product
Molecule 9	Molecule 10

The structure of the starting materials are drawn first in order to modelling the transition states. This is to further study the molecular orbital interactions. For the endo product, the maleic anhydride part was modelled from the top face of the cyclohexadiene molecule. Detailed optimisation was run by 3-21G basis set and together with the transition state Berny calculation to obtain the transition state geometry. The results are tabulated below:

	Endo transition state		Exo transition state
	AM1	B3LYP	AM1	B3LYP
Frequency/ cm-1	-810	-469	-812	-450
Bond forming length/ Å	2.18	2.25	2.19	2.30
Energy/ a.u.	-0.0516	-612.6835	-0.0504	-612.68

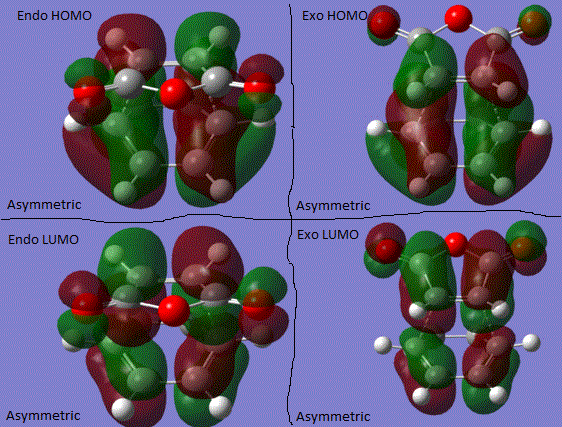
The results above show that the when the reaction is under the kinetic control, the transition state shows a lower energy, therefore it is more stable and make the product easier to form. According to the MO theory and orbital analysis, the molecular orbitals are antisymmetric. Since there are of the same symmetry, the MO theory said that when the two molecular orbitals are in the same symmetry, they interact and overlap to produce lower energy levels. Therefore, it can be seen that the cyclohexadiene highest occupied molecular orbitals will interact with the maleic anhydride lowest unoccupied molecular orbitals.

Looking at the transition state, it is obvious that the exo one has a large steric hindrince effect on the C=C double bonf with of the cyclic ring with the maleic anhydride part. This attributes to the higher energy after optimisation. However, this effect is not seen as large in the endo transition state. The stabilisation in the endo product can be summarised by a good orbital overlap between the C=C double bond with the C-O bonds in the molecule of maleic anhydride. Detailed effect can be seen below:

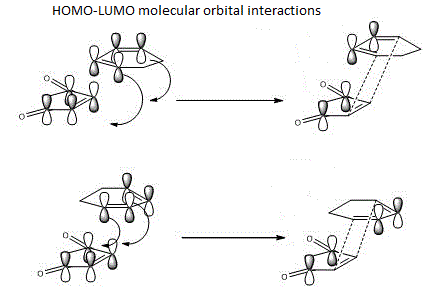
Conclusion

From the success of these experiments carried out above, it is seen that the computational calculations give very reasonable results and accurate prediction for the potential products. The relative total energies calculated for reactants, products, or transition states are competitive with the actual experimental results. Especially under kinetic conditions, the endo product for the Diels Alder reaction are successfully be predicted. These are the reason why nowadays, computiaonal chemistry plays a big role in up front researches.