Rep:Mod3:ypl07 The Transition State
The Cope Rearrangement
The aim of the experiment was to locate the low energy minima and determine the transition state structure on the 1,5-hexadiene potential energy surface and determine the preferred reaction mechanism.
Optimisation of the Reactants and Products
a) First optimisation of anti-1,5-hexadiene

An anti conformer of 1,5-hexadiene was drawn on Gaussview and optimised using HF/3-21G.
# opt hf/3-21g geom=connectivity 1,5-hexadiene_anti_optimisation 0 1
First optimisation of anti-1,5-hexadiene output file
| Energy / Hartree a.u. | Point Group | Structure |
| -231.693 | Ci | anti 2 |
b) First optimisation of gauche-1,5-hexadiene

A gauche conformation of 1,5-hexadiene was drawn on Gaussview and optimised using HF/3-21G.
# opt hf/3-21g geom=connectivity Gaushe structure optimisation (HF/3-21G) 0 1
First optimisation of gauche-1,5-hexadiene output file
| Energy / Hartree a.u. | Point Group | Structure |
| -231.688 | C2 | Guache 4 |
c) Hypothesis of lowest conformer
| Conformation | Energy / Hartree a.u. | Energy / kJ mol-1 | Relative energy (3 s.f.) / kJ mol-1 |
| anti-1,5-hexadiene | -231.69253506 | -608308.7508 | 0 |
| gauche-1,5-hexadiene | -231.68771617 | -608296.0988 | 12.7 |
The molecule which experiences the least steric hindrance should have the lowest energy. The Newman projection diagram of 1,5-hexadiene shows that the anti conformer has less steric hindrance than the guache conformer.
The results of the calculations also shows that the gauche conformer has higher energy than the anti conformer.
d) Identification of optimised strucutre
| Conformation | Structure |
| anti-1,5-hexadiene | anti 2 |
| gauche-1,5-hexadiene | gauche 4 |
e) Optimisation of the Ci anti2 conformation of 1,5-hexadiene
The Ci anti2 conformation of 1,5-hexadiene has already been located in part a).
f) Second optimisation of anti-2-1,5-hexadiene using DFT/B3LYP/6-31G*
The second optimisation was done by using the optimised anti-2-1,5-hexadiene output log file as the initial geometry and the method was DFT/B3LYP/6-31G*.
# opt rb3lyp/6-31g(d) geom=connectivity 1,5-hexadiene_anti_optimisation_B3LYP/6-31G(d) 0 1
Second optimisation of anti-2-1,5-hexadiene output file File:Ypl07DFTanti2.log
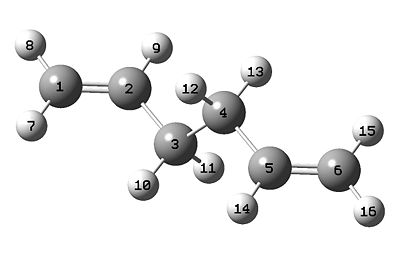
| Theory method | HF/3-21G | B3LYP/6-31G* | Experimental[1] |
| Energy /Hartree a.u. | -231.692(53506) | -231.611(71553) | |
| C1=C2 bond length /Å | 1.31(627) | 1.33(350) | 1.340 ± 0.003 |
| C2-C3 bond length/Å | 1.50(908) | 1.50(404) | 1.508 ± 0.012 |
| C3-C4 bond length/Å | 1.55(272) | 1.54(818) | 1.538 ± 0.027 |
| C1-C2-C3 bond angle/° | 124.8(02) | 125.3(02) | 124.6 ± 1.0 |
| C1-C2-C3-C4 dihedral angle/° | -114.6(60) | -118.7(74) | |
| C2-C3-C4-C5 dihedral angle/° | 180.0(00) | 180.0(00) | |
| Symmetry | Ci | Ci |
The symmetry of the molecule remained unchanged. The difference in bond length is within ±0.02 Å. The difference in bond angle is ± 0.5°. The difference in dihedral angle is ± 4°. The resulting geometry calculated by different methods is really similar. The energy calculated by different methods is not directly comparable. The energy calculated by HF/3-21G is lower than B3LYP/6-31G*. This is because 1,5-hexadiene is a simple molecule, and simpler basis set sometimes has better description than higher level basis set. However, B3LYP/6-31G* gives closer results to the literature value. Hence, B3LYP/6-31G* is a better basis set and gives more reliable results.
g) Frequencies of anti-2-1,5-hexadiene
The frequency calculation was done by using the second optimised anti-2-1,5-hexadiene output log file as the initial geometry and the method was DFT/B3LYP/6-31G*.
# freq rb3lyp/6-31g(d) geom=connectivity 1,5-hexadiene_anti_frenquency_B3LYP/6-31G(d) 0 1
Frequency analysis of anti-2-1,5-hexadiene output file
There are no negative frequencies and the lowest frequency is 73 cm-1. Hence all the frequencies are real and calculation converged.
Thermochemistry
| Sum of electronic and zero-point Energies / Hartree a. u. | -234.469176 |
| Sum of electronic and thermal Energies / Hartree a. u. | -234.461834 |
| Sum of electronic and thermal Enthalpies / Hartree a. u. | -234.460890 |
| Sum of electronic and thermal Free Energies / Hartree a. u. | -234.500743 |
Optimisation of the "Chair" and "Boat" Transition Structures
a) Optimisation of CH2CHCH2 and creating a guessed TS structure
A fragment of CH2CHCH2 is drawn on Gaussview and optimised using HF/3-21G method.
# opt hf/3-21g geom=connectivity CH2CHCH2 optimisation HF/3-21G 0 2
 |
|
|
| File:Ypl07CH2CHCH2 OPT1.LOG |
b) Optimisation and frequency analysis of guessed chair TS strucutre
A guessed chair TS structure was drawn on Gaussview using the optimised CH2CHCH2 structure as fragments. The distance of the terminal carbon atoms in the two fragments was set to be 2.2 Å. The guessed strucuture was optimised to TS(Berny), and a frequency analysis was also done at the same time.
# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity transistion_state_opt&freq_chair_guess 0 1
| File:Ypl07chairtsopt1.jpg | 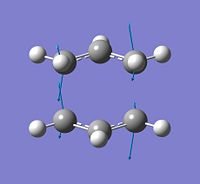 |
|
|
Animation of vibration at -818 cm-1 |
| File:Ypl07chairtsopt1.LOG |
The frequency analysis shows that there is only one imaginary vibration at -818 cm-1. It corrosponds to the bond forming and bond breaking of a [3,3]-sigmatropic rearrangement.
c) Optimisation of chair TS structure with frozen coordinate
The distance between two terminal carbons (2.2Å) was frozen via the redundant coordinate editor, using the optimised structure from the previous section. The partial frozen strucutre was optimised using HF/3-21G.
# opt=modredundant hf/3-21g geom=connectivity Transition_state_chair_Redundant_opt 0 1
 |
|
|
| File:Ypl07chairtsoptfreeze.LOG |
d) Optimisation of unfrozen chair TS structure
Using the optimised frozen chair TS structure as the initial coordinates, the structure was unfrozen by changing the bond to unidentifined and using derivative instead of add.
# opt=(ts,modredundant,noeigen) freq hf/3-21g geom=connectivity Transition_state_chair_Redundant_derivative_noeigen_opt&freq 0 1
| File:Ypl07chairtsoptunfreeze.jpg |
|
|
| File:Ypl07chairtsoptunfreeze.LOG |

| Method | Direct optimisation | Optimisation with redundant coordination |
| Energy /Hartree a.u. | -231.619(32247) | -231.619(32239) |
| C1=C2 bond length /Å | 1.38(926) | 1.38(923) |
| C2-C3 bond length/Å | 1.38(930) | 1.38(920) |
| C3-C4 bond length/Å | 2.02(038) | 2.02(069) |
| C1-C2-C3 bond angle/° | 120.5(01) | 120.4(92) |
| C2-C3-C4 bond angle/° | 101.8(48) | 101.8(52) |
| C1-C2-C3-C4 dihedral angle/° | -68.4(63) | -68.4(63) |
| C2-C3-C4-C5 dihedral angle/° | 54.9(72) | 54.9(87) |
The geometry of the chair transition state obtained by two different methods is similar. It shows that both methods of calculating the transition states are reliable.
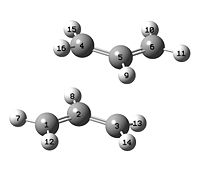
e) Optimisation of boat TS structure using QST2 method
| File:Ypl07anti2reactant.png | File:Ypl07anti2product.png |

The boat transition state structure was calculated by using the optimised anti-2-1,5-hexadiene conformer as the reactant and product, but the labelling of the atoms was altered to the corrosponding place after the rearrangment. The calculation was done using HF/3-21G.
# opt=qst2 freq hf/3-21g geom=connectivity Boat_transition_state_optimisation_using_qst2 0 1
Output file: File:Ypl07boattsopt1st.log
The output log file shows that the calculation failed with an error termination request processed by link 9999. This is because the calculation is starting with linear structure and the program did not consider rotation as a possibility for the transition state structure. As a result, the calculation reaches its limit before turning into the product.
| File:Ypl07anti2reactant2.jpg | 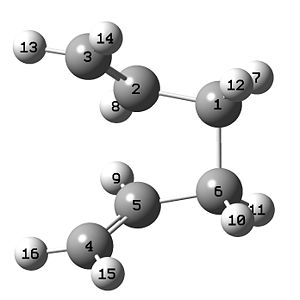 |
The second optimisation was done by changing the conformation of the reactant and product. The C2-C3-C4-C5 dihedral angle was changed to 0°. The C2-C3-C4 and C3-C4-C5 angle were set to 100°. The other settings were the same as for the first optimisation.
# opt=qst2 freq hf/3-21g geom=connectivity Boat_transition_state_optimisation_using_qst2_2nd 0 1
The frequency analysis shows that there is only one imaginary vibration at -840cm-1.
It corrosponds to the bond forming and bond breaking of a [3,3]-sigmatropic rearrangement.
| File:Ypl07boatts2nd.jpg | File:Ypl07boattsV1.jpg |
|
|
Animation of vibration at -840 cm-1 |
| File:Ypl07boattsopt2nd.LOG |
f) Analysis of the corrosponding reactants for each TS by IRC method
It is hard to find the corrosponding conformer by only looking at the structure of the transition state. However, the answer can be found by using the Intrinisic Reaction Coordinate or IRC method. It calculates the corrosponding structure by creating a series of points by taking small geometric steps towards the steepest slope of the energy surface.
Chair TS IRC
Using the output chk file of the chair transistion state as the structure for chair transition state. The job type was set to IRC, forwards calculation, calculating the force constant once and IRC maxpoint to 50. The calculation was done using the HF/3-21G basis set.
# irc=(forward,maxpoints=50,calcfc) hf/3-21g geom=connectivity Transition_state_chair_IRC_1st 0 1
Output file: File:Ypl07chairirc1st.log
File:Ypl07boatircgraph.jpg The resulting structure has an energy of -231.686(84123) Hartree a.u.. The energy does not match any of the lowest confomations in the Mod:phys3#Appendix_1. This is because the minimum energy is not reached and it can be solved by i) optimisation of the output structure ii) increasing the IRC maxpoint until it reaches the minimum energy geometry iii) calculate the force constant in every IRC step.
| Method (Jmol) | Input file | output file | Energy / Hartree a.u. | Conformer |
| File:Ypl07chairircopt.gjf | File:Ypl07chairircopt.log | -231.69166702 | gauche2 | |
| Dsapce | Dsapce | -231.69147170 | no match | |
| Dsapce | Dspace | -231.69166434 | gauche2 |
Both optimisation and compute-all-force-constant methods suggest that the corrosponding structure is gauche 2. However, increasing the IRC maxpoint to 100 still cannot obtain the minimum energy conformer. Since optimisation and compute-all-force methods give the same results, the easiest way (optimisation) is just as good as the most complicated way (compute-all-force-constant).
Boat TS IRC
Using the output chk file of the boat transistion state as the structure for the boat transition state.
The job type was set to IRC, forwards calculation, always calculating the force constant and IRC maxpoint to 100. The calculation was done using the HF/3-21G basis set. Finally the output file of IRC calculation was optimised.
Code for IRC calculation
# irc=(forward,maxpoints=100,calcall) rhf/3-21g geom=connectivity Transition_state_boat_IRC 0 1
File:Ypl07boatircgraph.jpg Code for optimisation
# opt hf/3-21g geom=connectivity Boat TS IRC opt 0 1
| Method(output file) | Jmol | Energy / Hartree a.u. | Conformer |
| always compute force constant | -231.683(02513) | no match | |
| Optimisation | -231.692(66119) | gauche3 |
The corrosponding conformer for boat transition state is gauche 3.
g) Activation energy analysis
Optimisation and frequency analyses using the B3LYP/6-31G* basis set were preformed for both chair and boat transition state structures. The activation energies were calculated using the anti-2 conformer as the reactant.
| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| Electronic energy /Hartree a.u. | Sum of electronic and zero-point energies at 0 K /Hartree a.u. | Sum of electronic and thermal energies at 298.15 K /Hartree a.u. | Electronic energy /Hartree a.u. | Sum of electronic and zero-point energies at 0 K /Hartree a.u. | Sum of electronic and thermal energies at 298.15 K /Hartree a.u. | |
| Chair TS | -231.619322 | -231.466701 | -231.461341 | -234.556983 | -234.414930 | -234.409009 |
| Boat TS | -231.602802 | -231.450930 | -231.445302 | -234.543093 | -234.402340 | -234.396002 |
| Reactant (anti2) | -231.692535 | -231.539542 | -231.532571 | -234.611712 | -234.469176 | -234.461834 |
1 hartree = 627.509 kcal/mol
| HF/3-21G | HF/3-21G | B3LYP/6-31G(d) | B3LYP/6-31G(d) | Expt.[2] | |
| Activation energy at 0 K /Hartree a.u. | Activation energy at 298.15 K /Hartree a.u. | Activation energy at 0 K /Hartree a.u. | Activation energy at 298.15 K /Hartree a.u. | Activation energy at 0 K /Hartree a.u. | |
| ΔE (Chair) | 45.7 | 44.7 | 34.0 | 33.1 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.6 | 54.8 | 41.9 | 41.3 | 44.7 ± 2.0 |
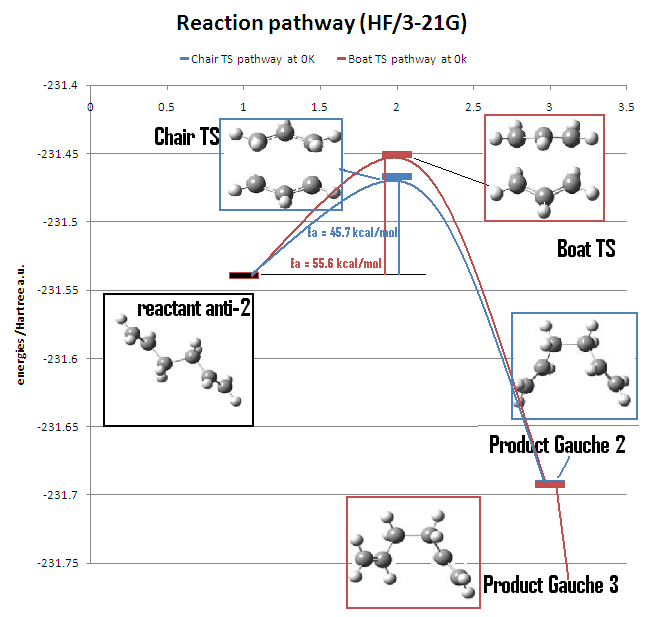
The activation energy calculated by B3LYP/6-31G* is once again closer to the experimental value than the activation energy calculated by HF/3-21G. The activation energy via the chair transition state is much smaller than the activation energy via the boat transition state. The resulting products for chair and boat transition states are similar in energy, hence the stabilities are similar. As a result, the Cope rearrangement via the chair transition state is more favourable than via the boat transition state.
LOG FILE:
| Structure | HF/3-21G optimisation | B3LYP/6-31G* optimisation | HF/3-21G frequency analysis | B3LYP/6-31G* frequency analysis |
| Boat TS | File:Ypl07boattshf.log | File:Ypl07boattsb3ylp.log | File:Ypl07boattshffreq.log | File:Ypl07boattsb3ylpfreq.log |
| Chair TS | File:Ypl07chairtshf.log | File:Ypl07chairtsb3ylp.log | File:Ypl07chairtshffreq.log | File:Ypl07chairtsb3ylpfreq.log |
| anti 2 | File:Ypl07anti2hf.log | File:Ypl07anti2b3ylp.log | File:Ypl07anti2hffreq.log | File:Ypl07anti2b3ylpfreq.log |
References and Citations
- ↑ G. Schultz, I. Hargitta, J. Mol. Struc., 1995, 346, 63-69. DOI:10.1016/0022-2860(94)09007-C
- ↑ Mod:phys3#Optimizing_the_.22Chair.22_and_.22Boat.22_Transition_Structures
