Rep:Mod3:yahtingkoh1

Cope Rearrangement

The Cope Rearrangement is a [3,3]-Sigmatropic pericyclic reaction, which involves the concerted migration of a group from one point of attachment to a conjugated system to another point of attachment, during which one σ bond is broken and another σ bond is made. In this module, the reactant is optimised to find the most stable conformer. The transition state is subsequently found, and IRC calculations would link the transition state to a particular conformer.

Optimisation of Reactants and Products

Optimising using Hartree-Fock 3-21G

1,5-hexadiene was optimised with the anti linkage using HF/3-21G level. The symmetry was determined by using the Symmetrize option in Gaussview. A few conformations were tried and the energies and symmetries were recorded (see below). The gauche conformer was also optimised using HF/3-21G. The gauche conformer is expected to be less stable than the anti conformer, since there are more steric repulsions in the gauche conformer. However, one of the gauche conformer is actually the most stable of all the conformers optimised. This can be explained by a stereoelectronic effect, which is called the CH-п interaction. It involves interaction between the п electrons of the C=C and the nearby vinyl proton, stabilising the gauche conformer.

Table 1: Conformers of 1,5-hexadiene and their relative energies

Conformer	Structure	Point Group	Energy/Hartrees	Relative Energy / kcal/mol
Anti1		Ci	-231.69254	0.08
Anti2		C2	-231.69230	0.23
Anti3		C2H	-231.68907	2.25
Gauche1		C1	-231.69266	0.00
Gauche2		C2	-231.69167	0.62

Optimising anti1 conformer using DFT/B3LYP/6-31G

The anti1 conformer (anti2 in Mod:phys3) was optimised at B3LYP/6-31G level. The final geometry looks very similar to that obtained from the HF optimisation. However, the energy was a lot lower.

Table2: Comparison of energy of geometry using different calculation methods

	HF/3-21G	DFT/B3LYP/6-31G
Energy / Hartrees	-231.69254	-234.55970
C=C bond length / Å	1.316	1.338
C1-C4 dihedral angle / degree	114.7	118.8

The geometry of the anti1 conformer differs only very slightly in the HF calculation compared to the DFT calculation. The C=C bond length is longer in the DFT calculation, indicating that the observed bond order of the C=C bond is smaller. Also, there is a slight difference in the C1-C4 dihedral angle observed.

Thermochemistry of the anti1 conformer

The frequency calculation allows for the thermochemistry of the molecule to be determined. This gives information about the vibrational energies and various contribution and correction terms. Since the energies are temperature-dependent, calculations were carried out, both at 0K and at 298.15K. The frequency calculations were done, using both HF/3-21G and B3LYP/6-31G.

Table3: Comparison of thermochemistry of anti1 conformer at different temperatures

	HF/3-21G 0K	HF/3-21G 298.15K	DFT/B3LYP/6-31G 0K	DFT/B3LYP/6-31G 298.15K
Sum of electronic and zero-point energies	-231.53907	-231.53954	-234.41580	-234.41625
Sum of electronic and thermal energies	-231.53211	-231.53257	-234.40852	-234.40895
Sum of electronic and thermal enthalpies	-231.53116	-231.53162	-234.40758	-234.40801
Sum of electronic and thermal free energies	-231.57043	-231.57091	-234.44740	-234.44785

The results show that the energies calculated are lower at 0K than at 298.15K. This is expected, since an increase in temperature would result in a greater contribution from the translational, rotational and vibrational modes. The last term is most negative, since the entropic contribution is taken into account.

Optimisation of Chair and Boat Transition States

The chair and boat transition state structures were optimised using three different methods.

Optimising Chair Transition State Using TS(Berny)

For the chair transition state, an optimisation was done using TS(Berny) directly by calculating the force constant at the beginning of the optimisation. The second way was to use the redundant coordinate to first freeze the bond that is to break/form to 2.2Å and optimise it to a minimum, and subsequently to use Bond Derivative and optimise as a transition state (TSberny).

(All using HF/3-21G)

Table4: Comparison of results between direct optimisation and via redundant coordinates

	TS(Berny)	TS(Berny) with redundant coordinate
Energy	-231.61932	-231.61932
Bond-forming length / Å	2.01968	2.02069
Bond-breaking length / Å	2.01988	2.02074
Imaginary Freq / cm-1	-818	-818

Both sets of calculations gave very similar results, and the differences are not significant considering the accuracy of Gaussian.

The vibrational mode at the imaginary frequency -818cm^-1 shows the asynchronous bond formation / bond breaking of the two bonds, where one bond breaks while the other forms. This corresponds to the [3,3]-sigmatropic pericyclic reaction of the Cope Rearrangement.

Following the reaction pathways: Chair TS

It was not possible to connect the various conformers of 1,5-hexadiene to the transition state. Hence the Intrinsic Reaction Coordinate (IRC) was calculated for the chair transition state (from the TS(Berny) with redundant coordinates above). The reaction coordinate was computed in the forward direction, using 50 points along the IRC. An initial calculation was done based on calculating the force constant once, but the calculation had yet to reach a minimum geometry. Another calculation was done with 50 points, with the force constant calculated at every point. The results are shown below:

Table5: IRC results: calculating force constants Once and Always

	Energy / Hartree	IRC Path	Gradient	Structure
Calculating force constant Once	-231.68605
Calculating force constant Always	-231.69165

The IRC path shows how the energy of the system decreases from the maximum at each point. For the IRC to be "successful", the energy of the system would have to plateau to the minimum, corresponding to a zero RMS gradient. From above, the IRC path for calculating force constant once shows the energy decreasing, but it has yet to plateau off. The RMS gradient is steadily decreasing, but it has yet to reach zero. Hence the IRC has not yet been able to conclusively reach a minimum geometry. It would be possible to get a more conclusive result, either by increasing the number of points (so that the calculation would continue decreasing along the IRC path), or to calculate the force constant at every point. From above, it is observed that the IRC path for calculating force constants always resulted in the IRC path plateauing to a nice minimum. The gradient has also decreased to zero. Hence, the IRC can now be used to link the transition state to a conformer optimised earlier. This corresponds to the gauche2 conformer above, with a calculated energy of -231.69165 Hartree.

Optimising Boat Transition State Using QST2

The boat transition state was optimised using QST2, where the reactant and product were specified, and Gaussian interpolates between the two structures to find a transition state between them. When the geometry of the reactant and product was not specified close to that of the boat transition state, the calculation failed. However, after modifying the geometry, the calculation was able to predict the boat transition state.

Table6: Optimising boat transition state using QST2

	QST2
Energy / Hartree	-231.60280
Bond forming length / Å	2.14075
Bond forming length / Å	2.14125
Imaginary Frequency / cm-1	-840

The energy of the boat transition state is higher than that of the chair transition state, which is expected, since there is greater steric repulsion in the boat structure. This would also mean that the boat transition state has a higher activation energy than the chair transition state (see below for further analysis).

The vibration mode at the imaginary frequency -840cm^-1 shows the bond-forming/breaking process of the cope rearrangement. This is an asynchronous bond formation, where the breaking of one bond corresponds to the forming of the other, which essentially is the cope rearrangement.

Following the reaction pathway: Boat TS

The IRC was calculated for the boat transition state, by calculating the force constant at every point along 50 points.

Table7: IRC path of boat TS

	Energy / Hartree	IRC Path	RMS Gradient	Structure
IRC (50 points, always)	-231.69166

The energy in the IRC path is observed to plateau to a minimum energy of -231.69166 Hartree, and the RMS gradient decreased to zero. Hence the IRC calculation using 50 points and calculating force constants at every point was successful in finding the minimum geometry. This corresponds to the gauche2 conformer obtained.

Activation Energies

The chair and boat transition structures were reoptimised using a higher level of theory, DFT/B3LYP/6-31G. Since the basis set used is more accurate, the energies computed are expected to be lower than that obtained from HF/3-21G, which is indeed the case. Frequency calculations were carried out to compare the differences in energies between the two levels of theory. The values are also computed at 0K and at 298.15K. The summary of the results are tabulated below.

Table8: Summary of energies

	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.46623	-231.46134	-234.55698	-234.41449	-234.40901
Boat TS	-231.60280	-231.45047	-231.44531	-234.54309	-234.40190	-234.39506
Reactant (anti1)	-231.69254	-231.53954	-231.53211	-234.61171	-234.46877	-234.46186

The activation energies (E_A or ΔE) via each transition pathway is calculated. The E_A for the transition state at 0K is found by taking the difference between the (sum of the electronic and zero-point energies) of reactant anti1 and the chair/boat transition state, multiplied by 627.509 kcal/mol. The E_A for the transition state at 298.15K is found by taking the difference between the (sum of the electronic and thermal energies) of reactant anti1 and the chair/boat transition state, multiplied by 627.509 kcal/mol. The results are summarised below:

Table9: Summary of activation energies via different pathways

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	46.00	44.41	34.06	33.16	33.5 ± 0.5
ΔE (Boat)	55.89	54.47	41.96	41.92	44.7 ± 2.0

The activation energy is always higher for the boat TS than the chair TS. This is expected, since the chair conformation of cyclohexane is the most stable conformation, where there is minimal steric repulsion since the structure is staggered. On the contrary, the boat conformation of cyclohexane is eclipsed, resulting in an increase in energy due to torsional strain from the eclipsing carbons and hydrogens.

Compared to the experimental values, the activation energies calculated using DFT/B3LYP/6-31G is definitely more coherent. The results for the chair transition state calculated using the DFT method actually matches very well with experimental results. There is a slight difference in that of the boat transition state, where the experimental activation energy is higher than that calculated.

Diels Alder Cycloaddition

The Diels Alder cycloaddition involves the concerted formation of two σ bonds between the termini of a diene and a dienophile. The prototypical reaction is studied here (Cis-butadiene + ethylene), and the reaction involving 1,3-cyclohexadiene and maleic anhydride is studied in a later section.

Prototypical Reaction: Cis-butadiene + ethylene

The structures of the reactants cis-butadiene and ethylene are optimised using Semi-Empirical/AM1 method. The HOMOs and LUMOs are observed and recorded.

Table10: HOMO and LUMO of cis-butadiene and ethene

	Cis-butadiene HOMO	Cis-butadiene LUMO	Ethylene HOMO	Ethylene LUMO
Molecular Orbital
Energy / Hartree	-0.34381	0.01707	-0.38775	0.05284
Symmetry (wrt plane)	Antisymmetric	Symmetric	Symmetric	Antisymmetric

The symmetry of the molecular orbitals can be determined by looking at whether there is a plane of reflection in the centre of the molecule. Hence, the HOMO of cis-butadiene is anti-symmetric (no plane of reflection), while the LUMO of cis-butadiene has a mirror plane in the middle of the C-C bond, and is symmetric.

Optimising the transition states

The transition state of the prototypical Diels Alder reaction is optimised using TS(Berny) with an initial guess. The guess structure was drawn using cyclohexene, without the forming/breaking bond. The calculation was done using Semi-Empirical/AM1 method. A second optimisation was done using the redundant coordinate method: first freezing the bond to 2.27Å and optimise to a minimum, followed by bond derivative and optimising to TS(Berny). The results are compared below:

Table11: Optimising of Diels Alder Transition State

	TS(Berny)	TS(Berny) with redundant coord.
Energy / Hartree	0.11165	0.11165
Bond forming length / Å	2.1195	2.1187
Bond breaking length / Å	2.1192	2.1196
Imaginary frequency / cm-1	-956	-957
Structure

Both calculations produced very similar results. The total energy, bond lengths and imaginary frequency corresponding to the Diels Alder bond forming/breaking process match each other very well.

Geometry of transition state: [Refer to Image above for TS(Berny), and enlarge if necessary to view atom labels.]

Table12: Geometry of Transition State

Bond length / Å or bond angles / °	TS(Berny)
C5 - C3	1.38
C3 - C1	1.40
C1 - C14	1.38
C14 - C11 (Bond forming)	2.12
C11 - C8 (Ethene bond)	1.38
C8 - C5 (Bond forming)	2.12
C8-C5-C3 angle	99.3
C1-C14-C11 angle	99.3
C14-C11-C8 angle	109.9

A typical sp³ C-C bond length is about 1.544Å, while a sp² bond length is 1.338Å . The van de Waals radius of carbon is 1.70Å .

The C-C bond length of the partly formed σ C-C bonds in the transition state is 2.12Å. This is longer than the typical sp3 C-C bond length, but shorter than twice the van der Waals radius of carbon. Hence it can be deduced that the C-C bond is in the process of forming, where it is not yet a full C-C bond.

Molecular Orbital Analysis of TS

The molecular orbital surfaces of the transition state structure was visualised.

Table13: HOMO and LUMO of transition state

	HOMO	LUMO
Molecular Orbital
Energy / Hartree	-0.32393	0.02315
Symmetry (wrt plane)	Antisymmetric	Symmetric

The HOMO is antisymmetric with respect to the plane dividing the C-C bond in butadiene and C=C bond in ethylene (see Mod:phys3). The LUMO is symmetric with respect to the plane.

The HOMO is made up of the antisymmetric cis-butadiene HOMO (п) and the antisymmetric ethene LUMO (п*). This corresponds to the Diels Alder reaction where there are 6п (ie, 4n+2) electrons, which under thermal conditions, will proceed via the Huckel topology with only suprafacial components. The orbitals involved are typical of cycloaddition reactions, where the HOMO of the diene interacts with the LUMO of the dienophile. The bond hence forms over the same face of the butadiene п system (suprafacial) and also over the same face of the ethene п system (suprafacial). The reaction is hence allowed, since it follows the pericyclic selection rules.

Vibrations of TS

Table14: Vibrations of Transition State structure

Frequency	Vibration	Mode of Vibration
-956		Synchronous formation of bonds: Carbon atoms on the ethylene move toward the butadiene carbons in a concerted motion
148		Rocking of ethylene component with respect to butadiene.

The vibration of the formation of the bonds show that both bonds form at the same time. This is expected, since the Diels Alder reaction is a cycloaddition reaction, which involves the concerted formation of two or more σ bonds between the termini of two or more conjugated π systems.

Activation Energies

The activation energies of the reaction are found by comparing the energies of the combined reactants and the transition states. The reactants and transition states were reoptimised with a higher level of theory, DFT/B3LYP/6-31G(d). Note that although the energies found using the DFT calculations look vastly different from those obtained from AM1, the absolute value of the energy is meaningless, and only the difference in energies is physically observable.

Table15: Summary of energies

	AM1	AM1	B3LYP/6-31G(d)	B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and thermal energies
		at 298.15 K		at 298.15 K
Transition State	0.11165	0.25945	-234.54390	-234.39691
Sum of Reactants Cis-butadiene and Ethene	0.07499	0.21883	-234.52586	-234.41422
Activation Energy ΔE	-	25.49	-	10.86

1,3-Cyclohexadiene + maleic anhydride

Optimisation of the reactants and endo/exo products

The reactants, 1,3-cyclohexadiene and maleic anhydride, were optimised using Semi-Empirical AM1 method. The transition structures for the endo and exo products were also optimised, using TS(Berny). Calculations were also done using the redundant coordinates method, but since the results are highly similar, they will not be reported here.

The reactants and transition states were reoptimised using a higher level of theory, DFT/B3LYP/6-31G(d).

Below shows the results from the transition state optimisations:

Table 16: Optimisation of Transition State

	Exo TS AM1	Exo TS B3LYP/6-31G(d)	Endo TS AM1	Endo TS B3LYP/6-31G(d)
Energy / Hartree	-0.05042	-612.67931	-0.05150	-612.68340
Sum of electronic and thermal energies / Hartree	0.14488	-612.48766	0.14368	-612.49179
Imaginary Frequency / cm-1	-812	-448	-806	-446

The energy of the endo transition state is lower than that of the exo transition state. This indicates that the endo transition state is favoured compared to the exo transition state.

Vibrations of the exo and endo transition states

Table17: Vibrations of the Exo and Endo TS

	Exo TS	Endo TS
Vibration

The vibrational modes of both isomers at the imaginary frequency show that the bond formation is a synchronous process. This corresponds to the Diels Alder cycloaddition reaction where there is concerted formation of two σ bonds.

Geometry of the transition states

The forming and breaking C=C п bonds are all observed to be about 1.40Å, which is consistent with the concerted formation of the bonds, since C=C of the maleic anhydride and the diene breaks in a concerted manner to form the new σ bonds as well as the new C=C bond.

In the exo transition state, the C-C through space distance of the CH₂CH₂ group and the maleic anhydride is 2.95Å. The corresponding CH=CH and maleic anhydride C-C through space distance in the endo transition state is 2.89Å. Hence, it appears that the endo transition state would be less stable, since there is an increase steric repulsion in the endo isomer. However, the endo isomer is in fact more stable, and this can be attributed to the secondary orbital overlap effect present only in the endo isomer.

Molecular orbitals of transition states

Below shows the HOMO and LUMO of the exo and endo transition states.

Table18: Molecular orbitals of exo transition state

HOMO	LUMO
-0.34275 Hartree	-0.04045 Hartree
Antisymmetric	Antisymmetric
One nodal plane (through center of molecule)	Two nodal planes (additional one due to anti-bonding overlap of diene and dienophile orbitals)

Table19: Molecular orbitals of endo transition state

HOMO	LUMO	HOMO - 12 (Orbital 22)
-0.34506 Hartree	-0.03570 Hartree	-0.54617 Hartree
Antisymmetric	Antisymmetric	Antisymmetric
One nodal plane	Two nodal planes	Phase of the -(C=O)-O-(C=O)- fragment of maleic anhydride corresponds to that of the diene

Secondary Orbital Overlap, by Imade

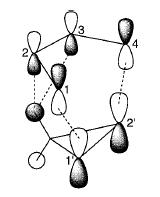
Imade et. al. described the primary and secondary orbital interactions in the cycloaddition of cyclopropene to butadiene. In this schematic representation, apart from the primary orbital interaction of the HOMO and LUMO conjugated systems, there exist a secondary interaction in the endo isomer, due to favourable overlap of the orbitals of the side groups of the alkene to the carbon orbitals on the diene.

A similar secondary orbital overlap is found in the endo isomer of the reaction between 1,3-cyclohexadiene and maleic anhydride. The anhydride fragment has orbitals which are in phase with the diene orbitals, allowing for a good overlap due to the small C-C through space distance. This can be observed in Orbital 22 shown above. This mixing of the orbitals result in a decrease in energy, overall resulting in the endo isomer being favoured despite an increase in steric repulsion.

Conclusion

Gaussian is able to perform many calculations, including the calculation and prediction of transition states. This would enable us to calculate the energy of transition states and hence predict the products of a reaction, especially if it is kinetically controlled. The Intrinsic Reaction Coordinate helps one to follow the path of a reaction, which is helpful in understanding pericyclic reactions. Also, molecular orbitals can be predicted, allowing for analysis of the stereochemical outcomes of reactions.