Rep:Mod3:xy307
Module Instruction
The purpose of the computational experiment is to characterize the transition states of Cope rearrangement and Diels-Alder cycloaddition reaction on the potential energy surface. In the experiment, the transition structures of larger molecules will be studied based on the molecular orbital methods, in which we solve the Schrodinger equation numerically and locate the transition structures based on the local shape of a potential energy surface. The calculation were carried out on Gaussian 03W and visualized on GaussView 3.0. CheDraw3D 12.0 ultra was also used to draw some structures during the experiment.
General Note on Accuracy and Convention
- Total energies are reported in atomic unit of Hartree (E'h').
- Relative energies are reported in kJ/mol, and are only valid for systems under the same type of calculation with identical number and type of atoms.
- The energy calculate has an error of ≈ 10 kJ/mol, which is equivalent of 0.00381 Hartree(1Eh = 2625.5 kJ/mol)
- The dipole moment is accurate to about 2 decimal places, i.e., 0.01 Debye.
- Frequencies in wavenumbers are by convention reported to the about 1 decimal places with stematic error of around 10%.
- Intensities are reported to the nearest integers by convention although accuracy is much less than this.
- Bond distances are accurate to ≈ 0.01 Å
- Bond angles are accurate to ≈ 0.1°
- 1 Hartree unit (Eh) = 2625.5 kJ mol-1 = 627.51 kcal mol-1
The Cope Rearrangement
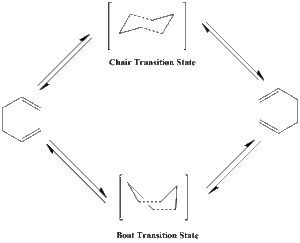
The Cope rearrangement is a [3,3]-sigmatropic shift rearrangement, which has been the subject of numerous experimental and computataional studies. Generally it is accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition state, with the "chair" conformation lying several kcal/mol higher in energy. In the tutorial we will use the Cope rearrangement of 1,5-hexadiene as an example of how to study a chemical reactivity problem. The objectives are to locate the low-energy minima and transition structures on the potential energy surface, and to determine the preferred reaction mechanism by Gaussian calculation.
Optimizing the Reactants and Products
Several conformation of 1,5-hexadiene are investigated to find out the lowest energy one. In general, the diene has two kinds of different stable conformations, gauche and anti. The difference of them are shown below:
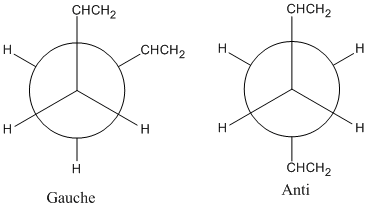
Within the two kinds of conformations, a number of conformers can exist by varying the orientation of the -CHCH2 groups. Ten stable comformation of 1,5-hexadiene are listed in Appendix 1.
Part A
A comformation of 1,5-hexadiene with an "anti" linkage is drawn by GaussView 3.0. The two vinyl groups are set to antiperiplanar position along C6-C9. Then the dihedral angle C4-C6-C9-C12 is set to 180.0°. The command for the optimization calculation is:
%mem=250MB # opt hf/3-21g geom=connectivity 0 1
Log file: COPE_REACT_ANTI.LOG
Results summary: Cope_anti_summary.jpg
The conformer has a Ci symmetry after symmetrizing, and it has an energy of -231.69254a.u..
Part B
A comformation of 1,5-hexadiene with an "gauche" linkage is drawn by GaussView 3.0. The dihedral angle of C1-C4-C6-C9 is set to -90°, the one of C4-C6-C9-C12 is set to -60°, and the one of C6-C9-C12-C14 is set to 30°. The energy of this conformer is expected to be a little higher than the anti conformer 1. It is because in Gauche conformers the two large groups are close to each other, and the methylene hydrogens are synperiplanar to the vinyl hydrogens in this conformer, which create a steric hindance.
The command for this optimization calculation is:
%mem=250MB # opt hf/3-21g geom=connectivity 0 1
Log file: COPE_REACT_GAUCHE.LOG
Results summary: Cope_gauche_summary.jpg
The conformer has a C1 symmetry after symmetrizing, and it has an energy of -231.68961a.u..
Part C
The antiperoplanar conformations are generally more stable than the gauche ones due to the large dihedral angle within the molecule. For gauche conformations, the bulky substituents nearby cause a steric strain. However, the most stable conformer of 1,5-hexadiene is gauche rather than antiperiplanar. This is because of the secondary orbitak overlap such as the hyperconjugation and π-π interactions. The gauche conformation is dwawn with the dihedral angle about 65° and then optimized. The result comformer is the gauche 3 in the Appendix 1, with a C1 symmetry. The command used for this calculation is:
%mem=250MB # opt hf/3-21g geom=connectivity 0 1
Log file: COPE_REACT_GAUCHE2.LOG
The MO analysis based on the optimized structure generates the HOMO and LUMO of the gauche 2 conformer.The HF/3-21g method and basis set are used with an additional key words pop=full and choosing full NBO analysis. The command used and the HOMO and LUMO MO are shown below:
%mem=6MW # hf/3-21g pop=(nbo,full) geom=connectivity 0 1
Log file: COPE_REACT_GAUCHE2NBO.LOG
 |
 |
It is obviuos that in the HOMO MO diagram there's a π-π interaction between the π orbitals of two double bonds.The stablizing interaction is a reason why gauche conformer is lower in energy. The LUMO indicates that the molecule experiences hypercongugation because the σ orbitals of the C-C bond interact with the π* orbitals of the double bonds. This is a stablizing stereoelectronic effect and hence another reason why the gauche conformation 3 is lower in energy.
The conformer has a C1 symmetry after symmetrizing, and it has an energy of -231.69266a.u.
Part D
Comparing the energy and geometry information to the Appendix 1, the above conformers correspond to these ones:
- Conformer 1 is equivalent to anti2 with energy at -231.69254 a.u.
- Conformer 2 is equivalent to gauche5 with energy at -231.68961 a.u.
- Conformer 3 is equivalent to gauche3 with energy at -231.69266 a.u.
Part E
The anti 2 conformer has already been optimized in Part A.
Part F
The optimization in Part A successfully achieved an energy in good agreement with the anti2 structure. The structure is then reoptimized on a higher level(DFT-b3lyp method/6-31g(d) basis set).
The command of DFT-B3LYP/6-31G(d) optimisation is:
# opt b3lyp/6-31g(d) geom=connectivity 0 1
Log file: COPE_REACT_ANTI_DFT.LOG Results summary: Cope_anti2_DFT_summary.jpg
The geometry difference between two optimizations is too tiny to be seen. The table below lists the details of the difference.
| Literature Value | HF/3-21G | DFT-B3LYP/6-31G(d) | |
|---|---|---|---|
| C=C Bond Length/Å | 1.340 | 1.316 | 1.333 |
| CH2-CH Bond Length/10-10m | 1.508 | 1.509 | 1.504 |
| CH2-CH2 Bond Length/10-10m | 1.538 | 1.553 | 1.548 |
| CH2-CH2-CH Bond Angle/Degree | 111.5 | 111.3 | 112.7 |
| CH2-CH=CH2 Bond Angle/Degree | 124.5 | 124.8 | 125.3 |
Part G
The "anti 2" conformer is optimized under the following command:
# freq rb3lyp/6-31g(d) geom=connectivity 0 1
Log file: COPE_REACT_ANTI2DFTFREQ.LOG Results summary: Cope_anti2_DFT_freq_summary.jpg
The thermodynamic data from the log file are as follows:
- Sum of electronic and zero-point Energies= -234.469195 a.u.
- Sum of electronic and thermal Energies= -234.461847 a.u.
- Sum of electronic and thermal Enthalpies= -234.460903 a.u.
- Sum of electronic and thermal Free Energies= -234.500782 a.u.
There is no imaginary vibration frequency, and the fully predicted IR spectrum is:
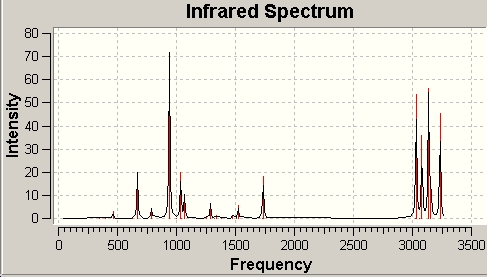
Some of the vibrations are listed below:
| Table - Vibrations of Anti 2 Conformer | |||||
|---|---|---|---|---|---|
| Vibrational Frequencies (cm-1) | Intensity | Assignment | |||
| 3234.2 | 45.4 | Alkene C-H Stretch | |||
| 3155.8 | 14.8 | Alkene C-H Stretch | |||
| 3136.8 | 56.1 | Alkene C-H Stretch | |||
| 3080.3 | 35.7 | Alkane C-H Stretch | |||
| 3031.3 | 53.6 | Alkane C-H Stretch | |||
| 1734.6 | 18.2 | Alkene C=C Stretch | |||
Optimizing the "Chair" and "Boat" Transition Structures
The purpose of this section is to optimize the two different imaginary transition structures of the Cope rearrangement of 1,5-Hexadiene and calculate their corresponding vibrational frequencies and potential energies. Then we could determine which transition state is more likely to be taken in real life.
Three different methods are used here: 1)Draw a structure which looks like the predicted transition state and then optimize it as a transition state by calculating the forece constant once. 2)Freeze the parameter using the redundant coordinate editor and optimize the structure as a transition state, then reoptimize the frozen parameters. 3)Use QST2 method to specify the reactant and product and label every atoms in the same way, then find the transition state by interpolate these two structures.
Part A
An allyl fragment (CH2CHCH2) is drawn in GaussView and optimised using the HF/3-21G method/basis set. The commant used is:
# opt hf/3-21g geom=connectivity 0 2
Log file: Allyl_Fragment_Optimization.LOG Results summary: Allyl_Fragment_Optimization_Summary.jpg
The structure has an energy of -115.82304 a.u., and a C2v symmetry. This is the building block of optimizing the transition state structures.
Part B
Two optimized allyl fragment are combined to form a guessed chair transition state. Then the chair approximation is subjected to optimisation and frequency analysis to the transition state with the additional keywords opt=noeigen. The force constant is set to be calculated once. The command used is:
# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity 0 1
Log file: COPE_GEOMETRY_CHAIR.LOG
Results summary: Cope_geometry_chair.jpg

The vibration frequency at -817.9cm-1 is the imiginary one. The vibration occurs at the position where bonds form in the rearrangement.
Part C
In this part the chair transition structure is optimized again using freezing coordinate method to make sure the structure we get is a transition state minimum rather than a different local minimum. The distances between terminal hydrogens are set to 2.2Å in the Redundant Coord Editor. Then the structure is optimized under the following command:
# opt=modredundant hf/3-21g geom=connectivity 0 1
Log file: COPE_GEOMETRY_CHAIR_FREEZE.LOG
Results summary: Cope_geometry_chair_freeze.jpg
The optimization structure is nearly the same comparing to the one optimized in Part B. However, if we look in details we could find the distances between two pair of terminal hydrogens are exactly 2.2Å as we set.
Part D
The frozen distances are set free and the structure is reoptimized without calculating the force constant. This requires using a normal guess Hessian modified to include the information about the two coordinates we are differentiating along. The command used is:
# opt=(ts,modredundant,noeigen) hf/3-21g geom=connectivity 0 1
Log file: COPE_GEOMETRY_CHAIR_FREEZE_OPT.LOG
Results summary: Cope_geometry_chair_freeze_opt_summary.jpg
The frozen coordinate method optimized structure resembles one in Part B. The table below lists the highly similarity of the two structure.
| Force Constant Method | Redundant Coordinate Method | |
|---|---|---|
| C-C Bond Length Allyl/10-10m | 1.389 | 1.389 |
| C-C Bond Length trans-Allyl/10-10m | 2.021 | 2.021 |
| Bond Angle within Allyl Fragment of Chair/Degree | 120.5 | 120.5 |
| Energy/a.u. | -231.61932 | -231.61932 |
| Spin | Singlet | Singlet |
| Charge | 0 | 0 |
| RMS Gradient/a.u. | 0.000022 | 0.000030 |
| Dipole/Debye | 0.0005 | 0.0001 |
| Point Group | C2h | C2h |
From the comparison it can be seen that both methods successfully achieve the same structure, which is the real transition structure of Cope rearrangement.
Part E
In the part the boat transition structure will be optimized using QST2 method. The method interpolates the reactant and product to reach a transition stae. As a result, the atoms must be labelled in the same way. This is done by editing the atim list.
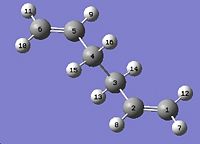
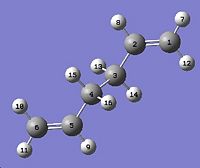
This is then subjected to the following:
# opt=(qst2,noeigen) freq hf/3-21g geom=connectivity 0 1
Log file: COPE_GEOMETRY_BOAT_OST.LOG The job fails because the QST2 method cannot rotate about any of the bonds, so the output structure looks like a more dissociated chair transition state. To solve the problem the angles must be modified before optimization.The C2-C3-C4-C5 and C2-C1-C6-C5 dihedral angles are set to 0° and the C2-C3-C4 and C2-C1-C6, and C3-C4-C5 and C1-C6-C5 bond angles are 100°, as the diagram below.
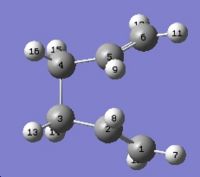
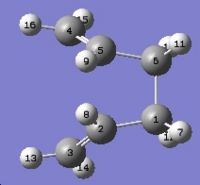
The optimization is run again under the following command:
# opt=(qst2,noeigen) freq hf/3-21g geom=connectivity 0 1
Log file: COPE_GEOMETRY_BOAT_OST2.LOG
Results summary: Cope_geometry_boat_qst2.jpg
Part F
The chair transition state resembles the gauche 2 conformer of 1,5-hexadiene and the boat transition state looks like the gauche 3 conformer. However, it is impossible to predict which conformer the reaction paths from the transitions structures will lead to. The intrinisic reaction coordinate method is applied here on each conformer to find the geometric minimum from the transition state. Is is also noted that the IRC calculation won't produce a minimum initially. There are three ways to solve the problem: 1)take the last point on the IRC and run a normal minimization; 2)restart the IRC and specify a larger number of points until it reaches a minimum; 3)redo the IRC and specify that we want to calculate the force constant at every step. The third method is used here. The advantage is that this one is the most reliable and with the help of work station the calculation still can be finished in a reasonable time.
Firstly, do the calculation on the chair transition state, with a 50 step limit and force constants.
The command used is:
# irc=(forward,maxpoints=50,calcall) rhf/3-21g geom=connectivity 0 1
The log file can be found at D-space reference: [1]

The structure corresponds to Gauche 2 since they have exactly the same energy.
The same calculation is excuted on the boat transition state.
# irc=(forward,maxpoints=50,calcall) rhf/3-21g geom=connectivity 0 1
The log file can be found at D-space reference: [2]
The structure corresponds to Gauche 3.
The figure below shows the IRC and RMS curves when calculating force constant at every step.
 |
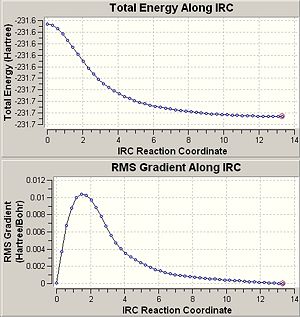 |
Part G
In this part we will estimate the activation energy of the Cope rearrangement. In order to compare with the real value, the higher level optimization(DFT-B3LYP/6-31G(d)) is used, followed by frequency analysis at the same level to get some thermodynamic data. The chair transition state is optimized under the following command:
# opt=(ts,noeigen,modredundant) rb3lyp/6-31g(d) geom=connectivity 0 1
The log file can be found at D-space reference: [3] The frequency analysis is then run via the following command:
# freq rb3lyp/6-31g(d) geom=connectivity 0 1
The log file can be found at D-space reference: [4]
The same procedures are carried out on the boat transition state. The log file for optimization can be found at D-space reference: [5]
The log file for vibration analysis can be found at D-space reference: [6]
The tables below summarise the differences from these calculations
| Electronic Energy (HF 3-21G) | Sum of Electronic and Zero-point Energies at 0K (HF 3-21G) | Sum Electronic and Thermal Energies at 298K (HF 3-21G) | Electronic Energy (B3LYP 6-31G d) | Sum of Electronic and Zero-point Energies at 0K (B3LYP 6-31G d) | Sum Electronic and Thermal Energies at 298K (B3LYP 6-31G d) | |
|---|---|---|---|---|---|---|
| Chair TS | -231.619 | -231.467 | -231.461 | -234.559 | -234.417 | -234.409 |
| Boat TS | -231.603 | -231.451 | -231.445 | -234.545 | -234.405 | -234.396 |
| Anti 2 (Reactant) | -231.693 | -231.540 | -231.533 | -234.612 | -234.469 | -234.462` |
| HF 3-21G at 0K | HF 3-21G at 298K | B3LYP 6-31G d at 0K | B3LYP 6-31G d at 298K | Experimental at 0K | |
|---|---|---|---|---|---|
| Chair TS | 45.81 | 45.18 | 33.27 | 32.63 | 33.5 |
| Boat TS | 55.85 | 55.22 | 42.04 | 40.16 | 44.7 |
The comparison indicates that the chair transition structure has a lower energy and less steric strain, which is more favourable to proceed in the Cope Rearrangement.
The Diels-Alder Cycloaddition
The Diels-Alder reaction is one of the most common pericyclic reactions and proceed via a concerted process.The π orbitals of the dieneophile form new σ bonds with the π orbitals of the diene simutaneously. For a successful Diels-Alder reaction, the HOMO-LUMO interaction involved in the bond forming process must have the same symmetry. If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed.The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap is possible and the reaction is forbidden. The purpose of this section is to prove the theory above. First, a simple Diels-Alder reaction between butadiene and ethene is investigated. Then we move to a more complicated reaction between maleic anhydride and cyclohexa-1.3-diene, which is stereoselective. Typically, this reaction produces an endo product in favour of an exo isomer. In computational chemistry we can calculate the relative energy of them and find out why the selectivity happens.[1]
Optimization of Butadiene and Ethene
Cis-butadiene is drawn in GaussView and optimised by the semi-empirical AM1 method:
# opt am1 geom=connectivity 0 1
Log file: CISBUTADIENE_AM1.LOG Then ethene is optimized in the same way. Log file: ETHENE_AM1.LOG The HOMO and LUMO MO for both reactants are visualized. They are either symmetric or antisymmetric. Only the orbitals with same symmetry can interact in the reaction. The orbitals are shown below:
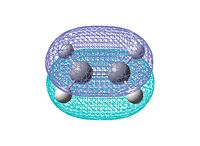 |
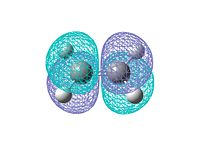 |
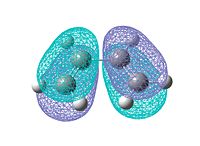 |
 |
From the diagams above we can see only the HOMO of cis-butadiene and LUMO of ethene, or the HOMO of ethene and LUMO of cis-butadiene have the same symmetry which allows interaction to take place. Since the diene is electron rich, the interaction between HOMO of butadiene and LUMO of ethene will dominate. There is no electron donating group attached to the diene or electron withdrawing group linked to the dienophile, so it is easy to predict the reaction is relatively slow.
Reaction between Butadiene and Ethene
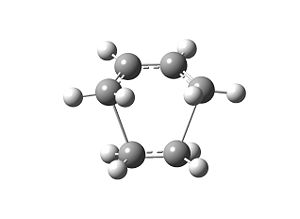
QST 3 method is used in this part to optimize the transition state structure. The optimized(AM1 level) reactant, product and pseudo-transition state are placed in GaussView with the right order and optimized with the following command:
# opt=(calcall,qst3,noeigen) freq am1 geom=connectivity 0 1
Log file: DA_CYCLOHEXENE_AM1_QST3.LOG
This is a thermal π4s + π2s cycloaddition reaction, via a Hückel transition state. The reaction is symmetrically allowed.


The HOMO of the transition state is antisymmetric. It is formed by interaction between the HOMO of cis-butadiene and LUMO of ethene. The LUMO is symmetric, which is formed from the HOMO of ethene and LUMO of cis-butadiene.
The H2C-CH bond length is a bit longer than in butadiene, being 1.38Å. The C2-C3 bond length is 1.39 Å, which is between C-C and C=C(1.34Å[2]), indicating that the the bond order is increasing now. The terminal carbons of two fragments both have a distance of 2.11Å. For carbon, the van der Waals radius is 1.9Å[3]. The distance is shorter than the sum of the radius, which shows there is some interactions between them now.
There is an imaginary frequency at -955.7 cm-1 observed in the vibration analysis, which corresponds the interaction between terminal carbons. The lowest positive frequency observed is at 146.9 cm-1. It is asymmetric including a torsional component of the "ethene" fragment.
 |
 |
 |
Stereoselectivity of cycloaddition between Maleic Anhydride and Cyclohexa-1,3-diene
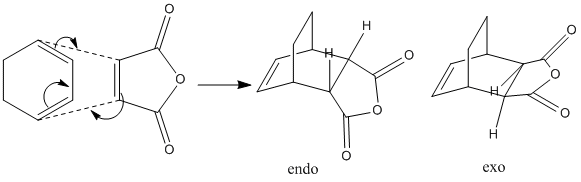
The reaction between cyclohexa-1,3-diene and maleic anhydride is more complicated because it can result in two different product, endo- or exo-. QST3 method is employed again to analysis the transition states.
Due to the complexity of the structure, ChemDraw 3D is used to visualize the transition structure and then import them to GausView. The structures are optimized using AM1 semi-empirical method. After that the QST3 method are executed under the following commands:
# opt=(calcall,qst3,noeigen) freq am1 geom=connectivity 0 1
Exo log file inD-space: [7] Endo log file in D-space: [8]
 |
 |
The exo isomer has higher energy(-0.05042a.u) than the endo isomer(-0.05150a.u.). The exo structure is less stable due to the repulsion between the anhydride oxygen and the hydrogen on the ring.
Based on the optimized structure, the MOs of the transition states are obtained using the same method as previous example.
 |
 |
 |
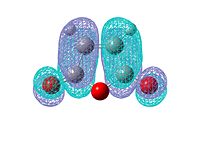 |
The anhydride group is a strong electron-withdrawing group. Therefore it prefers electron donation from the HOMO of cyclohexadiene into the LUMO of the anhydride. This HOMO-LUMO interaction forms the HOMO of both transition state structures.
 |
 |
 |
 |
Further observation of the HOMO of the endo isomer reveals the nodal character is such that all the oxygen atoms in the anhydride functionality have nodes in the middle, and lobes both above and below. The central oxygen atom however has lobes extends outward towards the other two oxygen atoms, rather than projecting upwards/downwards as seen in the other oxygen atoms. The same applies to the exo isomer but with smaller blending between the lobes. The maleic anhydride bearing three strong electron withdrawing oxygen atoms. Hence it is much more reactive than butadiene and ethene. From the MO diagram we can also find that the LUMO is still a bonding orbital, which means it is thermodynamically easily available for Lewis base.
The lower energy (about 2.9kJ/mol) endo transition state suggests this pathway is kinetically favourable comparing to the exo one. In addition to the larger steric strain seen in the exo isomer, the reason for this stabilisation in energy for the endo isomer can be explained by the secondary orbital overlap effect, which is illustrated in the figure below.
 |
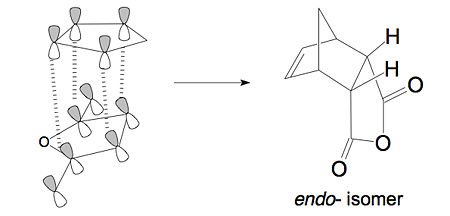 |
The difference implied between the Figures above is that the endo isomer is more stable relative to the exo isomer, due to the additional electron donation from the π-system (HOMO) of cyclohexa-1,3-diene into the orbitals of the electron-poor (LUMO) maleic anhydride, i.e. the middle p-orbitals of the diene with the vacant p-orbitals of the carbonyl groups in the dienophile. We have found that secondary orbital overlap do exist and are responsible for at least an important part of the observed stereocontrol. Although the absolute magnitude of this kind of interactions is small, its impact on the stereochemical outcome is very important, because of the exponential relationship between the difference in activation energies and the kinetic product ratio. Of course, other factors can operate in different cycloadditions, and their relative importance can vary from one case to another, but the magnitude of SOI cannot be discarded a priori.[4]This secondary orbital overlap, together with the reduced steric repulsion, makes the endo isomer the more favoured transition state. In this case, these two factors act along the same direction, to stablise the endo transition state.
References
- ↑ E. Goldstein, Brett Beno, and K. N. Houk J. Am. Chem. Soc., 1996, 118 (25), pp 6036–6043. DOI:10.1021/ja9601494
- ↑ J. C. Kotz, P. Treichel, Chemistry & Chemical Reactivity, Volume 2, 2008, 7th Edition, 387. ISBN 978-0-495-38713-8
- ↑ R. C. Smoot, R. G. Smith, J. Price, Merrill Chemistry, 1999, 316. ISBN 978-0-028-25527-9
- ↑ Ana Arrieta and Fernando P. Cossıo J. Org. Chem., 2001, 66 (18), pp 6178–6180. DOI:10.1021/jo0158478
