Rep:Mod3:shl108

Cope Rearrangement

Optimizing the Reactants and Products

Optimisation with HF/3-21G

HF/3-21G level of Gaussian calulation is used to optimise the 1,5-hexadiene in this section.

Table 1: Optimisation of Conformers

	anti1	Gauchea	Gauchea3
File Type	.chk	.chk	.chk
Calculation Type	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF
Basis Set	3-21G	3-21G	3-21G
Final Energy / a.u.	-231.69260236	-231.69153034	-231.69266122
RMS Gradient Norm / a.u.	0.00001239	0.00000795	0.00000413
Dipole Moment / Debye	0.20	0.13	0.34
Point Group	C2	C2	C1
Log file	File:Anticonformer1.LOG	File:GaucheConformerA.LOG	File:GAUCHE3.LOG
conformer identified from Appendix 1	anti1	gauche4	gauche3

Both structures have C₂ symmetry. My hypothesis is that gauche conformation is expected to be less stable than the anti conformation due to steric effect. In this case, gauche 4, indeed, has a lower energy than anti 2.However, gauche 3 is the most stable conformation of 1,5-hexandiene. This can be explained by stereoelectronic which is due to the CH-π interaction. The favourable donation of electron density from the πC=C orbital of the C=C double bond into the σ*C-H orbital of the adjacent vinyl proton has lowered the overall energy of the molecule.

Optimisation of Anti2-Conformer with DFT/B3LYP/6-31G(d)

Table 2: Optimisation of C_i anti2 conformation of 1,5-hexadiene by HF/3-21G and B3LYP/6-31G*

anti2
File Type	.chk	.chk
Calculation Type	FOPT	FOPT
Calculation Method	RHF	RB3LYP
Basis Set	3-21G	6-31G(D)
Final Energy / a.u.	-231.69253506	-234.61170276
RMS Gradient Norm / a.u.	0.00006411	0.00003510
Dipole Moment / Debye	0.00	0.00
Point Group	Ci	Ci
C1-C4 dihedral angle / °	114.7	118.5
Log file	File:Anticonformer2.LOG	File:Anticonformer2DFT.LOG

The final energies of this molecule calculated by HF/3-21G and B3LYP/6-31G* give two different values, -231.69253506 and -234.61170276 a.u. respectively. Although the dipole moment and point group do not have any changes, the C1-C4 dihedral angles are obtained differently by HF/3-21G and B3LYP/6-31G* which are 114.7° and 119.5° respectively.

Table 3:IR spectrum of anti2 conformation of 1,5-hexadiene optimised by B3LYP/6-31G*

298.5 K	0K

Comparison of Energies at 0K and 298K

The sum of electronic and zero-point energies, the sum of electronic and thermal energies, the sum of electronic and thermal enthalpies and the sum of electronic and thermal free energies at 298.15K and 0K are calculated and shown in the table below.

Table 4: Temperature-Dependence of Anti2-1,5-hexadiene Energies

Energies	298.15K	0K
Sum of electronic and zero-point Energies (Hartree/Particle)	-234.469211	-234.468774
Sum of electronic and thermal Energies (Hartree/Particle)	-234.461854	-234.461428
Sum of electronic and thermal Enthalpies (Hartree/Particle)	-234.460910	-234.460483
Sum of electronic and thermal Free Energies (Hartree/Particle)	-234.500825	-234.500376
Output file	File:DFToptFREQUENCY.LOG	File:FREQUENCY2.LOG

As the temperature increases, the molecule has more energy to access more vibrational state which give more vibrational modes. Thermal energy is temperature dependent, so at high temperature, the contribution of thermal energy increases.

Optimizing the "Chair" and "Boat" Transition Structures

The transition states of Cope rearrangement of 1,5-hexadiene are proposed as below:

For route b, it is the most unlikely pathway. This is because the dissociation energy of the C-C bonds is much higher then the activation energy and there is no cross product produced experimentally. For route c, it has the same problem with high energy TS compare with the activation barrier. Therefore, it is unliky to happen as well.

Optimisation of Chair Transition State

Comparison of TS Optimisation Methods

Table5: Allyl fragment (CH2CHCH2) and optimized by HF/3-21G level

CH2CHCH2

Checkpoint file

File:CB1.LOG

Table6: Optimising chair transition state using Berry TS and Redundant Coord Editor

	Berry TS	Freeze Coordinate	Redundant Coord Editor
Energy / Hartree	-231.61932246	-231.61518364	-231.61932201
Bond breaking/forming length / Å	2.02	2.20	2.02
Imaginary Frequency / cm-1	-818	N/A	-818
chair transition state	[1]	N/A	[2]
Checkpoint file	File:BerryTSChair.fchk	File:FreezeChairCoordinate.fchk	File:DerivativeCoordinate.fchk

Two different methods give the same results for the energy of the transition state. Both methods give the same bond breaking/forming length,at 2.02 Å. Vibration at -818 cm-1 shows the bond breaking/forming transition state of this electrocyclic rearrangement. This vibration shows the reaction mechanism is asynchronous, which means one bond breaks and the other forms simultaneously.

Intrinsic Reaction Coordinate

Table7: IRC results: calculating force constants Once and Always

	Energy / Hartree	IRC Path	Gradient	Structure	Files
Calculating force constant Once	-231.68906651				http://hdl.handle.net/10042/to-5577
Calculating force constant Always	-231.69164800				http://hdl.handle.net/10042/to-5576

The HF/3-21G optimised chair TS is further investigated with Intrinsic Reaction Coordinate (IRC) calculation. The aim is to simulate the transformation from the chair TS down the potential energy surface to the final product of the reaction.

At first,the IRC calculation was performed with 50 points on the IRC pathway with computating the force constants only once. The result of the calculation showed no bond formation process. This can be explained that the calculation was incomplete, as a 1,5-hexadiene structure was expected. In addition, analysis of the IRC pathway showed that points on the pathway do not reach an asymptotethe which indicaten the minimum of the potential curve has not been reached. Th calculation was repeated with the same number of points on the IRC pathway with computating the force constants at every step. This allows the IRC calculation to determine if it is moving along the minimum energy pathway down the potential energy surface, and make changes to the pathway when necessary. As a result, a conformer of 1,5-hexadiene was observed, and the IRC pathway has reached the minimum of the potential curve.

The optimised chair transition structure connects to the gauche2 conformer.

Optimisation of Boat Transition State

Table8: Optimising boat transition state using QST2

	QST2
Energy / Hartree	-231.60280222
Bond forming length / Å	2.14
Imaginary Frequency / cm-1	-840
Vibration	[3]
Log file	File:BOATOPTQST2.LOG

QST2 is more reliable method that Berry TS. With QST2, the structures of reactant and product are taken as consideration in the calculation.Hammond's postulate[4] can be applied to a more accurate prediction of the TS. In Computational Chemistry, if more information is provided in the calculation, a more accurate result should be obtained. The imaginary frequency, -840 cm^-1, shows that a transition state was found. The vibration indicates that the bond dissociation/formation is asynchronous, a stepwise mechanism.

Activation Energies of Chair and Boat Structures

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466700	-231.461341	-234.556983	-234.414929	-234.409008
Boat TS	-231.602802	-231.450928	-231.445309	-234.543093	-234.402342	-234.396008
Reactant (anti2)	-231.692535	-231.539542	-231.532571	-234.611702	-234.468774	-234.461854

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.70	33.79	33.16	33.5 ± 0.5
ΔE (Boat)	55.61	54.76	41.69	41.69	44.7 ± 2.0

Table5: Files of optimisation

	HF (298.15K)	HF (0K)	DFT (298.15)	DFT (0K)
Chair	File:BerryTSChair.out	File:BerryTSchair0K.out	File:DFTChair.out	File:DFTChair0K.out
Boat	File:BOATOPTQST2.LOG	File:Boatopt0K.out	File:BoatoptDFT.out	File:BoatoptDFT0K.out
Anti2	File:DFToptFREQUENCY.LOG	File:FREQUENCY2.LOG	File:Anti2HFopt.out	File:Anti2HFopt0K.out

The calculated activation energies agrees with the experimental values for both chair and boat structures.

Diels Alder Cycloaddition

For both optimisations of the transition states of cycloaddition, QST2/AM1 method is used to perform the calculation.

Optimisation of cis-butadiene and ethene

Table9: Optimising of Transition State of butadiene and ethene

Butadiene			Ethene
MO	Representation	Symmetry	MO	Representation	Symmetry
HOMO	HOMO	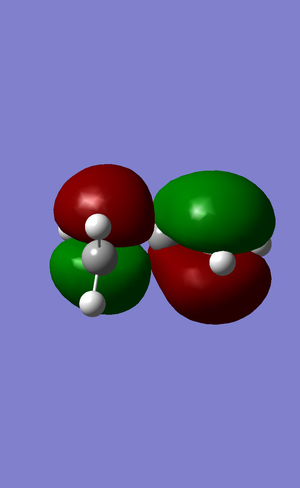Antisymmetric	HOMO	HOMO	Symmetric
LUMO	LUMO	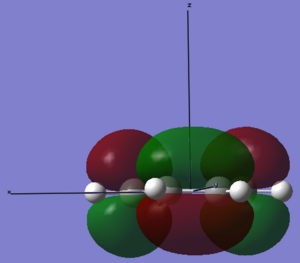Symmetric	LUMO	LUMO	AntiSymmetric
Files	Butadiene[5]			Ethene [6]

The LUMO of cis-butadiene can be reflected in the plane of symmetry of the molecule. Therefore, it is symmetric. For the HOMO of cis-butadiene, the phases are inverted while the orbital is reflected in the plane of symmetry, so it is anti-symmetric. The symmetry of the orbitals can give informtaion of which orbitals are going to react and how the stereoelectronic control will be. The HOMO of ethene is symmetric with respect to the plane of symmetry and the LUMO is anti-symmetric. In quantum theory, only the orbitals with the same symmetry can interact. Therefore, the HOMO of cis-butadiene will interact with the LUMO of ethene, and the LUMO of cis-butadiene will interact with the HOMO of ethene.

This can be proved in the transition state calculation.

Computation of the Transition State geometry for the prototype reaction

Table10: Optimising of Diels Alder Transition State of butadiene and ethene

	QST2
Bond forming length / Å	2.12
Vibrational frequency / cm-1	-956	147
Vibration
Sum of electronic and zero-point Energies/a.u.	0.253274
Sum of electronic and thermal Energies/a.u.	0.259451
Sum of electronic and thermal Enthalpies/a.u.	0.260395
Sum of electronic and thermal Free Energies/a.u.	0.224014
Structure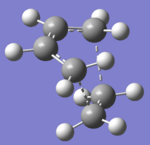
Files	[7]

HOMO

LUMO

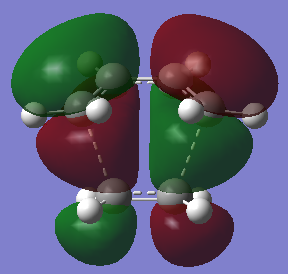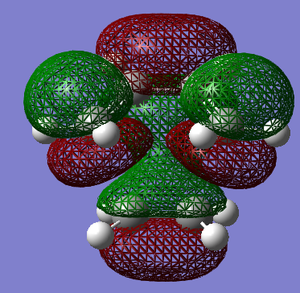The bond breaking/forming length in the TS is 2.12 Å. The typical sp3 C-C bond is 1.53 Å, and sp2 C=C bond is 1.34 Å. Van de Waals Radius of carbon is 1.70 Å. The bond breaking/forming length is shorter than the Van de Waals interaction betweent two carbon atoms which is 3.40Å. However, it is longer than sp³ and sp² C-C bond length. This means that the carbon atoms are approaching each other within the Van de Waals radii region for bond formation, but the bonds are partially formed and broken. This fits with the transition state theory. According to the quantum theory,the symmetry of the molecular orbital formed form the overlap of two atomic orbitals, have to be the same as that of the initial orbitals. In addition, only filled orbitals can overlap with empty orbitals and vice versa. This can be explained by Pauli exclusion principle[8] and Hund's rule[9]. The HOMO is antisymmetric, whereas the LUMO is symmetric. The negative frequency at -956 cm^-1 which indicates formation of the two bonds is synchronous. The lowest positive frequency at 147 cm^-1 is the rocking vibration which indicates the motion of the viration is asynchronous.

The regioselectivity of the Diels Alder Reaction

Table11:Summary Table of the Endo and Exo Transition Structures optimised by QST2/AM1

	Endo	Exo
Total Energy/ a.u.	-0.05159413	-0.05050324
Dipole Moment/ Debye	6.17	5.57
Bond breaking/forming length/ Å	2.16	2.17
Imaginary Frequency / cm-1	-805	-812
Structure	Endoproduct.mol2	Exoproduct.mol2
Files	[10]	[11]

The endo transition state have a more negative energy than exo transition state. It means the activation barrier of obtaining endo transition state is lower. If the final product is selective to the endo product, the reaction will be controlled kinetically.

Table12:Summary Table of the Molecular Orbitals for the Endo and Exo Transition Structures

	Transition States
Molecular Orbital	Endo TS	Exo TS
HOMO
Symmetry	Antisymmetric	Antisymmetric
LUMO
Symmetry	Antisymmetric	Antisymmetric

The C-C bond breaking/forming length is 2.16 Å in the endo transition state, and 2.17 Å in the exo transition state. Endo transition state has a shorter C-C bond breaking/forming length than exo transition state which indicates the stronger interaction and more likely to form bond. In addition, the distance between the carbon atom of the carbonyl group in the maleic anhydride and the non-reacting carbon atom of the C=C double bond on the cyclo-1,3-hexadiene. In the endo transition state, it is 2.89 Å, while in the exo transition state, it is 3.78 Å. This distance shows the secondary orbital overlap between the πC-C orbital of cyclo-1,3-hexadiene and π*C=O orbital of maleic anhydride, which can overall stabilise the transition state. The shorter distance in the endo transition state than the exo transition state indicates that secondary orbital overlap only occur in endo transition state.

Table13:Summary of the Geometries of the Endo and Exo Transition Structures

Parameter	Endo / Angstroms	Exo / Angstroms
Length of new/forming C-C sigma bonds	2.16	2.17
Distance between C=O group and opposite CH2CH2 group	2.89	3.78
Distance between the anhydride C=C and the diene C=C	2.71	2.64
Distance between the two C=O groups	2.28	2.28