Rep:Mod3:man7286
Introduction
This module uses computational techniques to work out the most stable transition state of various reactions and therefore which product is preferred. The program Gaussview5 was used to draw the molecules and the calculations were performed by Gaussian.
Tutorial: Cope Rearrangement of 1,5-Hexadiene
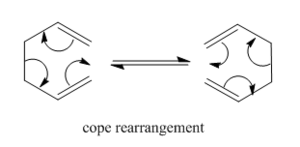
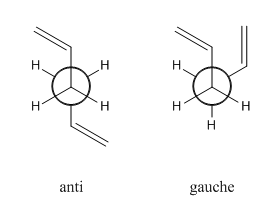
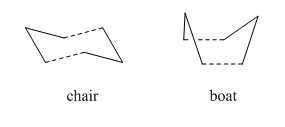
The cope rearrangement is the rearrangement of a terminal diene. The aim for this tutorial is to determine the most stable intermediate through which the rearrangement occurs. The molecule can be in one of two conformations, based on the four central carbon atoms, anti- or gauche, and the rearrangement proceeds through either a chair or boat intermediate.
The method and basis set used for the optimisation calculations was HF/3-21G. A molecule of 1,5-hexadiene was drawn in two conformers- anti and gauche. Both conformers were optimised and the results are shown in Table 1.
| Conformer | Image | Energy/Eh | Point Group |
|---|---|---|---|
 |
-231.69260 | C1 | |
 |
-231.69153 | C2 |
The anti conformer is lower in energy by 2.8 kJ mol-1, but these are only two of the ten possible conformers of 1,5-hexadiene: there are three further anti and 5 further gauche conformers
Reoptimisation of One Conformer at Higher Accuracy Method
One of the other anti conformers has an energy of -231.69254 Eh.
This conformer was reoptimised using a higher accuracy method and basis set: B3LYP/6-31G*.
The reoptimised energy was -234.55970 Eh. A summary of the energies from the log file is shown in Figure 5.
Optimising the Chair and Boat Transition Structures
The method and basis set used for the following calculations was HF/3-21G.
Allyl Fragment Optimisation
Chair Transition State Optimisation and Frequency Calculation
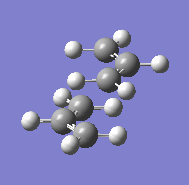
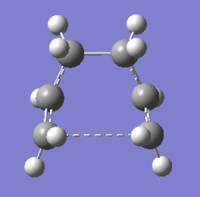
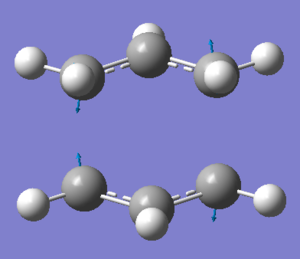
The "guess" transition state was made up from two allyl fragments and is shown in Figure 7. The structure was then optimised to a transition state (Berny) with the force constants calculated once. The optimised structure had an imaginary frequency at -818 cm-1, which corresponds to the Cope rearrangement, i.e. one C-C bond lengthens as the other contracts. The vibration is shown in Figure 8. The energy for the transition state was -231.61932 and the bond breaking/forming distance in the transition state was 2.02 Å.
Optimisation of Chair Transition State by Frozen Coordinate Method
The guess transition state was optimised this time using the frozen coordinate method. Using the redundant coordinate editor bonds between the terminal carbons were added and frozen to 2.20 Å. The structure was then optimised to a minimum. The optimised structure was opened and the bonds were optimised by adding bond derivatives in the redundant coordinate editor, this was then optimised to a transition state (Berny). The optimised structure is shown in Figure 9, the bond breaking/forming distance was 2.02 Å.
Boat Transition State Optimisation and Frequency Calculation
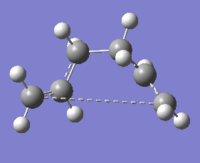
The boat transition state comes from the second anti conformer of 1,5-hexadiene. The QST2 method was used to optimise the boat transition state. This method requires the input file to contain the reactant and product molecules, as shown in Figure 10. It was very important to make sure that all the atoms were labelled correctly. The file was optimised to a transition state (QST2) but the calculation failed, the final geometry is shown in Figure 11. As you can see the final geometry ressembles the chair transition state. The reason that the calculation failed is because instead of rotating the central C-C bond Gaussian just translated the C3 groups, causing the bonds to cross over in the middle.
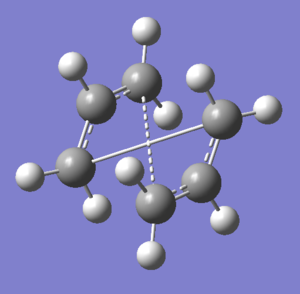
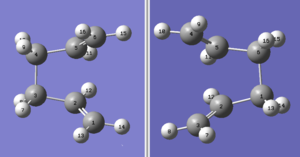
The input file was modified as shown in Figure 12. The dihedral angle of the four central carbon atoms was set to zero, this gave a better starting geometry for the optimisation. This calculation was successful and the transition state had an imaginary frequency at -842 cm-1, again corresponding to the Cope rearrangement. This is shown in Figure 13. The energy for the optimised transition state was -231.60280 Eh and the bond breaking/forming distance was 2.14 Å.
Intrinsic Reaction Coordinate
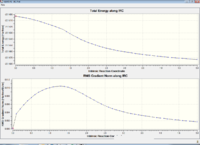
The intrinsic reaction coordinate aims to predict the conformer which the transition state leads to, this is done by following the minimum energy path from a transition structure via small geometry steps in the direction where the energy gradient is steepest. As the reaction coordinate was symmetrical in this case the IRC was only computed in the forward direction. Originally the force constants were only calculated at the beginning of the calculation and 50 steps were chosen. Table 2 shows the results of the original IRC calculations.
| Transition State | Chair | Boat |
|---|---|---|
| Graphs |  |
|
| Final Geometry |  |
|
| Energy/Eh | -231.68907 | -231.67199 |
| Optimised Final Geometry |  |
|
| Energy of Optimised Final Geometry | -231.69167 | -231.69266 |
These are clearly not the correct structures as the final geometries doesn't ressemble any of the product/reactant conformers. This means the calculations havn't reached the correct minimum. Therefore further modifications to the calculations were needed.
Re-run IRC computing Force Constants at Every Step
The input file was modified to calculate the force constants at every step.
| Chair | Boat | |
|---|---|---|
| Graphs |  |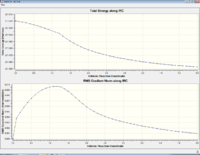
|
| Final Geometry Energy/Eh | ||
| Optimised Final Geometry Energy/Eh |
Both final geometries clearly ressemble one of the gauche conformers, the same for both transition states.
Reoptimisation of Chair and Boat Geometries
The chair and boat transition state geometries were reoptimised and the frequency calculations were performed at the B3LYP/6-31G level.
| Energy/Eh | -234.50547 | -234.49291 |
| Bond Length/Å | 2.04 | 2.26 |
| Imaginary Frequency/cm-1 | -561 | -505 |
The activation energies were calculated by taking the difference in energies between the relavent reactant/product conformers and the transition states. Figure 16 shows the reaction coordinate for the chair and boat transition states, the activation energy for the chair transition state was 190.7 kJ mol-1 and for the boat was 234.1 kJ mol-1.
Diels Alder Cycloaddition
The AM1 semi empirical MO method was used for following calculations, unless otherwise stated.
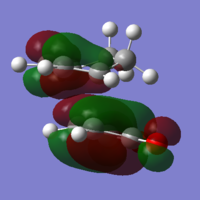
Reaction Between cis-Butadiene and Ethene
| Energy/Eh | 0.04880 | 0.02620 | 0.11163 | -0.01620 | ||||
| Bond Length/Å | n/a | n/a | 2.12 | 1.52 | ||||
| Orbital | HOMO | LUMO | HOMO | LUMO | HOMO | LUMO | HOMO | LUMO |
 |
 |
 |
 |
 |
 |
 |
| |
| Energy/Eh | -0.34389 | 0.01712 | -0.38776 | 0.05284 | -0.32394 | 0.02316 | -0.34877 | 0.04877 |
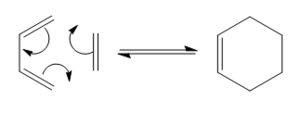
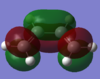
With respect to the plane of the molecule, the HOMO of cis-butadiene is anti-symmetric and the LUMO is symmetric, whereas for ethene both the HOMO and LUMO are anti-symmetric. The interaction between the HOMO of cis-butadiene and the LUMO of ethene leads to the HOMO of the transition state, which is anti-symmetric. This interaction is allowed because the two orbitals have the same symmetry. The transition state LUMO is also anti-symmetric and arrises from the interaction between the HOMO of ethene and the LUMO of cis-butadiene. The partly formed C-C bond length in the transition state is 2.12 Å which shortens to 1.52 Å in the cyclohexene product. A standard C-C bond length is 1.54 Å[1] so this new C-C bond is very slightly shorter, probably because it is part of a ring system. The Van der Waals radius for carbon is 1.70 Å[2] therefore at the transition state bond length of 2.12 Å the Van der Waals radii are overlapping i.e. Van der Waals forces are in place.
The transition state has an imaginary frequency at -956 cm-1 corresponding to the symmetric stretching of the partly formed C-C bonds, this shows that the bonds are formed at the same time.
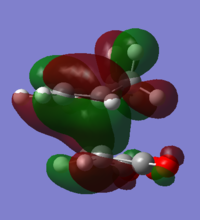
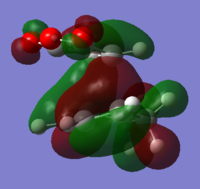
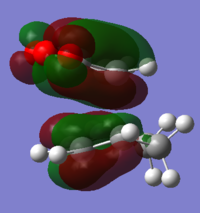
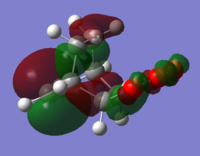
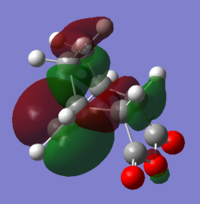
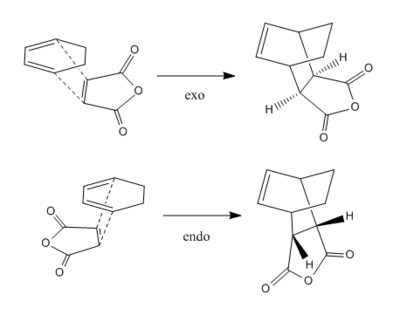
Reaction Between Cyclohexa-1,3-diene and Maleic Anhydride
Optimisation of Reactants
| Cyclohexa-1,3-diene | Maleic Anhydride | |||
|---|---|---|---|---|
| AM1 | HF/3-21G | AM1 | HF/3-21G | |
| Energy/Eh | 0.02770 | -230.54323 | -0.12184 | -377.18003 |
| HOMO |  |
| ||
| -0.32182 Eh | -0.44185 Eh | |||
| LUMO |  |
| ||
| 0.01679 Eh | -0.05947 Eh | |||
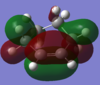
Looking at the HOMO and LUMOs of the reactants in Table 6 it is clear that when the two reactants come together the HOMO of maleic anhydride is of the correct symmetry to interact with the LUMO of cyclohexa-1,3-diene and the HOMO of cyclohexa-1,3-diene is of the correct symmetry to interact with the LUMO of maleic anhydride. The latter is more likely as these two orbitals are closer in energy.
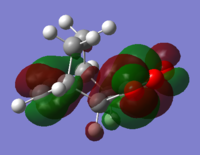
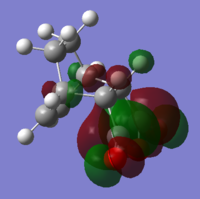
Optimisation of exo- and endo- Transition States
| Conformer | ||
| Energy/Eh | -0.05050 | -0.05159 |
| Bond Length/Å | 2.17 | 2.16 |
| Imaginary Frequency/cm-1 | -812 | -806 |
| HOMO |  |
|
| -0.34146 Eh | -0.34507 Eh | |
| LUMO |  |
|
| -0.04188 Eh | -0.03569 Eh |
| Conformer | ||
| Energy/Eh | -605.60359 | -605.61037 |
| Bond Length/Å | 2.26 | 2.23 |
| Imaginary Frequency/cm-1 | -647 | -645 |
The endo conformer is lower in energy and therefore more stable. At the semi-empirical AM1 level the energy difference is 2.86 kJ mol-1 and at the HF/3-21G level the difference is 17.8 kJ mol-1. The exo transition state is more strained because of steric hindrance for the sp3 hyrdogens and the -(C=O)-O-(C=O)- group.
Both imaginary frequencies correspond to symmetric stretching of the new C-C bonds, showing that the bonds form at the same time. The exo imaginary frequency is slightly more negative than the endo, corresponding to the slightly longer partial C-C bond.
Optimisation of Products
| exo | endo | |||
|---|---|---|---|---|
| AM1 | HF/3-21G | AM1 | HF/3-21G | |
| Energy/Eh | -0.15997 | -605.38888 | -0.16023 | -605.72132 |
| Bond Length/Å | 1.54 | 1.54 | 1.54 | 1.55 |
| HOMO |  |
| ||
| -0.38788 Eh | -0.38708 Eh | |||
| LUMO |  |
| ||
| 0.00602 Eh | 0.01078 Eh | |||
The endo product is lower in energy by 872.8 kJ mol-1 (HF/3-21G)
References
- ↑ http://www.science.uwaterloo.ca/~cchieh/cact/c120/bondel.html Accessed 11:35 28/3/11
- ↑ http://en.wikipedia.org/wiki/Carbon Accessed 11:50 28/3/11