Rep:Mod3:louis
Module 3
This module involved the use of computational methods to model the transition structures of the Cope rearrangement and the Diels Alder Cycloaddition reactions. The main program used was Gaussian/Gaussview, with Chembio3D being employed occasionally to draw the initial structures of molecules.
The Cope Rearrangement
The Cope rearrangement of 1,5-hexadiene is an example of a [3,3] sigmatropic pericyclic reaction and in the this case the product is the same as the reactant due to the the reaction just being a rearrangement. An overview can be seen below.
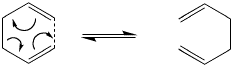
Optimizing the Reactants and Products
a)
Firstly a molecule of 1,5-hexadiene with an anti linkage was drawn in Chembio3D and then imported into Gaussview. The molecule was then optimized at the HF/3-21G level and the molecule with the structure below was produced.

Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.ANTI2_OPT.LOG
The structure above belongs to the point group Ci and had a total energy of -231.69254 a.u.
b)
A molecule of 1,5-hexadiene with a gauche link was then drawn in Chembio3D and then imported into Gaussview where it was optimized at the HF/3-21G level.
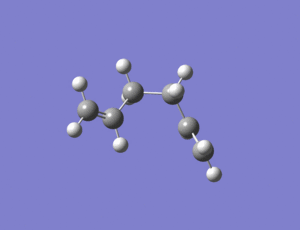
output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.gauche3.LOG
The above structure has C2 symmetry and so belongs to to the C2 point group. It has a total energy of -231.69266 a.u. The gauche conformer has a lower energy than anti conformer, but I would have predicted that the anti conformer would be lower in energy due to less steric interactions.
c)
From the results obtained previously I thought that the anti conformer found was perhaps not the lowest energy conformer and so the structure was adapted slightly by changing the angle between the two central carbons (3 and 4)and an optimization at the HF/3-21G level was run but the structure that returned was the same as the one already found, proving that it was the lowest energy anti conformer. It also seems slightly unusual that a gauche conformer is the lowest energy conformer when one would expect an anti conformer to be and this maybe due to gauche interactions whereby the C-H bonds donate electron density into the opposite C-Cantibonding orbitals.
d)
A comparison between the structures obtained and the ones listed in Appendix 1 [1] were made. The anti conformer was identified as the anti2 conformer and the gauche conformer was identified as the gauche 3 conformer. The table below shows the collated information.
| Conformer | Energy/a.u | Point group | Appendix Conformer | Appendix Energy/a.u | Appendix point group |
|---|---|---|---|---|---|
| anti | -231.69254 | Ci | Anti 2 | -231.69254 | Ci |
| gauche | -231.69266 | C2 | Gauche 3 | -231.69266 | C2 |
From the above table it can be seen that the computed conformers match very well to the ones listed in the appendix. Anti 2 is in fact the lowest energy anti conformer, as is Gauche 3 when compared to the other gauche conformers. The gauche 3 conformer is also the lowest energy conformer overall.
e)
The anti 2 conformer has already been optimized and its energy matched the value given in the appendix.
f)
The anti 2 conformer was then re-optimized at a higher level, the B3LYP/6-31G(d) level and the structure below was produced.
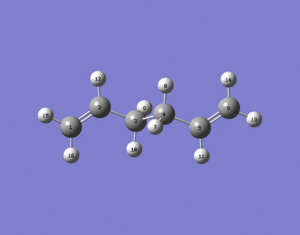
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.ANTI2_REOPT.LOG
It can be seen that visually the anti 2 conformer optimized at a higher level looks no different to when it was optimized at the HF/3-21G level. However when the summary file was viewed it was evident that the re-optimized structure at the B3LYP/6-31G(d) level was lower in energy (234.66117 a.u. Even though the energies differ when a different level of theory is used, they are not really comparable due to the accuracies of the two methods being different. The geometries were therefore also looked at.
| Bond | HF/3-21G | B3LYP/6-31G(d) |
|---|---|---|
| C=C/Ao | 1.32 | 1.33 |
| C3-C4/Ao | 1.55 | 1.55 |
| C-C/Ao | 1.51 | 1.50 |
| C-H/Ao | 1.08 | 1.09 |
| Bond Angle | HF/3-21G | B3LYP/6-31G(d) |
|---|---|---|
| C1-C2-C3/degrees | 124.8 | 125.3 |
| C2-C3-C4/degrees | 111.5 | 112.7 |
| C3-C4-C5/degrees | 111.3 | 112.7 |
| C4-C5-C6/degrees | 124.8 | 125.3 |
From the data given above the bond lengths are very similar for the two anti2 conformers with the bond lengths being slightly larger when the method and basis set used is B3LYP/6-31G(d. This is also the case with the bond angles, as they are also slightly larger in value for the B3LYP/6-31G(d) optimized structure. This comparison has highlighted the fact that using a different method can give a slightly different outcome in the structure produced. It is probably right in saying that the structure produced by the B3LYP/6-31G(d) method is the more accurate one due to the the better accuracy of the method employed.
g)
A frequency calculation was then carried out on the B3LYP/6-31G(d) optimized anti 2 conformer.
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.ANTI2_FREQ.LOG
The IR spectrum can also be viewed:
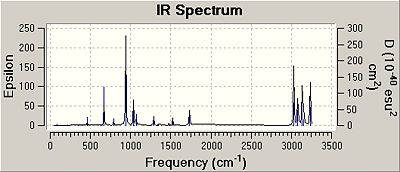
The frequencies were checked to make sure that they were all positive and they all were, confirming that the structure was the fully optimized one and at an energy minimum.
The thermochemistry data from the frequency file can be seen below.
| Energy Type | Energy/a.u |
|---|---|
| Sum of electronic and zero point energies | -234.4692 |
| Sum of electronic and thermal energies | -234.4619 |
| Sum of electronic and thermal enthalpies | -234.4609 |
| Sum of electronic and thermal free energies | -234.5008 |
Optimizing the chair and boat transition states
This section involves looking at the structure of the transition states of the Cope rearrangement by using different methods including calculating the force constants once, using the redundant coordinate editor and by using the QST2 method.
All the calculations below were carried out at the HF/3-21G level, unless otherwise stated.
a)
Firstly an allyl fragment C3H5 was drawn in Gaussview and then optimized.
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo1.ALLYL_OPT.LOG
b)
The optimized allyl fragment was then duplicated and orientated into a guess chair configuration with the two allyl fragments approximately 2.1Ao apart.

An Opt + Freq calculation was then carried out on the guess structure with "optimization to a TS(berny)" being selected along with calculate force constants once. In the additional keywords section "opt=noeigen" was added. The structure below was produced.
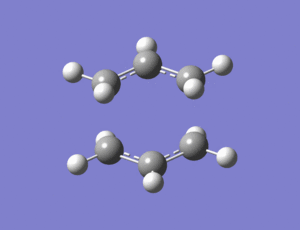
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo1.CHAIR_TS_1.LOG
The vibrational analysis results were then checked and there was only one imaginary frequency of 818cm-1 which when animated showed that it corresponded to the cope rearrangement. You can clearly see the symmetrical movements towards bond formation/breakage which are in antiphase to each other.
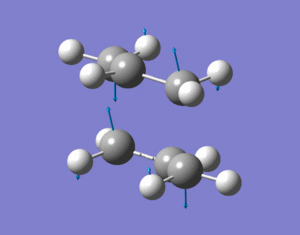
c)/d)
The frozen coordinate method was then carried out on the original guess chair TS structure. Firstly the redundant coordinate editor was used to fix the "bond' lengths between the two allyl fragments to 2.2Ao and this allows the rest of the TS to be optimized first. The structure was then optimized and this gave a structure which was very similar to the one produced i part b) apart from the bonds between the two allyl fragments were fixed to 2.2Ao. The "bonds' between the two allyl fragments were then unfrozen and Hessians were assigned to them and this allows the "bond" lengths to be optimized. The structure was then optimized again. The resulting structure resembled the structure produced in part b) very closely, as visually no difference could be seen.
Output file c) https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo1.CHAIR_TS_FROZEN.LOG Output file d) https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo1.CHAIR_TS_FROZEN_2.LOG
When a comparison was made between the two chair TS structures there was no notable difference in them visually or by looking at their geometries. Both were found to have an inter allyl bond distance of 2.02Ao, a C-C bond length of 1.39Ao and a C-H bond length of 1.07Ao. The bond angles were also the same: dihedral angle between the ends of a chair was 55 degrees and angle between the two allyl fragments was 111 degrees. The energies of the two TS structures were -231.61932230 a.u for the Ts(berny) method and -231.61932239 a.u for the frozen coordinate method. Therefore, it seems that both methods have produced the same transition structure and that it does not matter which method you choose to generate it, but with the first method you must be careful in choosing a good guess for your transition structure.
e)
This section involves generating the structure for the boat transition state by using the QST2 method. This method analyzes the reactant and the product and tries to find a TS structure that is in between the two. Firstly the anti 2 structure from before was duplicated and arranged as shown below into a reactant/product configuration. The atoms were also relabeled so that the product corresponded to the reactant.

An opt + freq calculation was then carried out and optimize to a TS (QST2) was selected along with never calculate force constants. This calculation failed and produced an odd looking transition state that was similar to the chair TS generated earlier, but slightly deformed. This was because the original geometries selected for the reactant/product were too far from how they should be. Therefore the the reactant and product were rearranged into the forms as shown below. This was achieved by setting the C2-C3-C4-C5 dihedral angle to zero degrees and the C2-C3-C4 and C3-C4-C5 angles to 100 degrees.
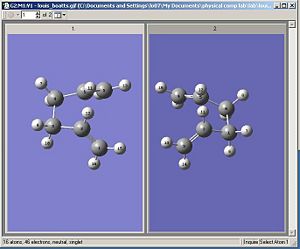
The opt + freq calculation was then carried out again and this time it worked producing the boat transition structure shown below. The boat TS had only one imaginary frequency and it was at 849 cm-1.

f)
Both the transition states seem to have a resemblance to a gauche conformer, but to confirm this an IRC calculation was carried out on both the chair TS and the boat TS.
Chair TS
An IRC calculation was carried out on the chair TS from the frozen coordinate method and the force constants were only calculated once and the IRC was only calculated in the forward direction. After 24 steps the below structure was produced.
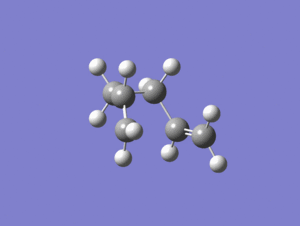
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.CHAIR_IRC50.LOG
The above structure looked quite close to the gauche 2 conformer but was optimized again using a normal optimization calculation and the below structure resulted. The Gauche 2 conformer is also provided for reference. They both had the same energy of -231.69167 a.u.
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.CHAIRIRC50OPT.LOG
 |
 |
Boat TS
When the IRC calculation was carried out on the boat TS the structure which resulted resembled the Gauche 3 conformer slightly. This occurred after 44 steps. The structure was then optimized using a normal optimization calculation, but the resulting structure did not seem to have changed and still looked like a twisted gauche 3 conformer. It is shown below.
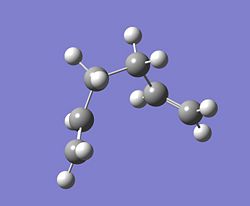
g)
The chair and boat TS structures were then optimized again but at the B3LYP/6-31G(d) level. A frequency analysis was also carried out on each TS.
Chair TS
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.CHAIR_REOPT.LOG
Output file:https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.CHAIR_FREQ.LOG
The bond between the two allyl fragments of the chair transition state was found to be 1.97 angstroms which is lower than the value generated by the HF/3-21G level of theory.
The table below shows a comparison of the Thermochemistry data all done at the B3LYP/6-31G(d)level.
| Energy Type | Anti2 | chair TS | boat TS |
|---|---|---|---|
| Sum of electronic and zero point energies/a.u | -234.46920 | -234.41492 | -234.40234 |
| Sum of electronic and thermal energies/a.u | -234.46186 | -234.40900 | -234.39601 |
| Activation enrgy/a.u | n/a | 0.05428 | 0.06687 |
| Total energy | -231.69254 | -234.55698 | -234.54309 |
It is clear from the data above that the Cope rearrangement would go via a chair transition state as the activation energy is lower.
The Diels Alder Cycloaddition
Al the calculations below were carried out at the semi-empirical AM1 level.
Part 1
Firstly cis butadiene and ethylene were optimized.
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.cisBUTADIENE_OPT.LOG
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.ETHYLENE_OPT.LOG
Their HOMO and LUMO molecular orbitals were then visualized:
| Cis butadiene MO | symmetry | MO image | Ethylene MO | MO image | symmetry |
|---|---|---|---|---|---|
| HOMO | 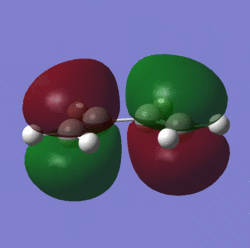 |
antisymmetric | HOMO |  |
symmetric |
| Lumo | 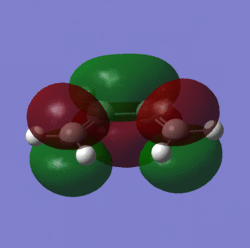 |
symmetric | LUMO | 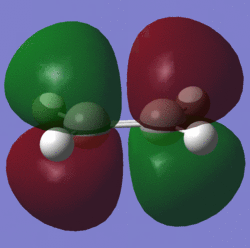 |
antisymmetric |
From the images above it is evident that the HOMO of one can interact with the LUMO of the other but HOMO-HOMO and LUMO-LUMO interactions cannot occur.
Part 2
The method chosen to optimize the transition structure of the Diels alder reaction between ethylene and cis-butadiene was the calculating the force constants once at the beginning and the optimization of a TS(berny) method. The cis-butadiene and ethylene were arranged in a similar way to the one shown in the instructions. The bond length between ethylene and cis-butadiene was around 2.1Ao. An opt + freq calculation was then carried out with the result shown below along with the imaginary vibration (-817.5 cm-1)and the lowest real vibration (166.9 cm-1).
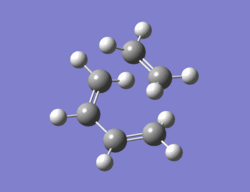 |
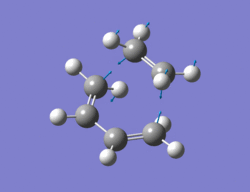 |
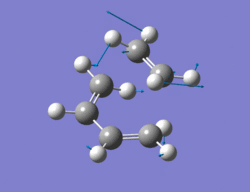 |
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.TS_GUESS_TWO.LOG
The imaginary vibration corresponds to the concerted formation of the the two new sigma bonds whereas the lowest real frequency is asynchronous and involves a twist of the TS. The imaginary vibration is synchronous. The Van der Waals radius of the carbon atom is 1.7Ao[2]. The new bond lengths being formed are 2.21Ao and the C-C bond lengths are 1.4Ao and the C=C bond lengths are 1.37Ao, being slightly larger than a literature value of 1.34Ao.
The MO's of the transition state:
| MO | Picture | Symmetry |
|---|---|---|
| HOMO | 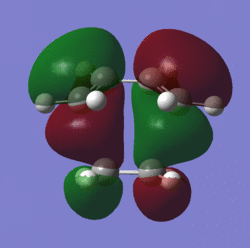 |
antisymmetric |
| LUMO | 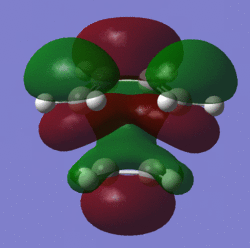 |
symmetric |
When looking at the MO's of the transition state it is evident that it is the HOMO of ethylene and the LUMO of cis-butadiene that form the TS's LUMO and it is the HOMO of cis-butadiene and the LUMO of ethylene which form the HOMO of the TS.
Part 3
This section looks at the Diels alder reaction between cyclohexa-1,3-diene and maleic anhydride which can result in either an exo or endo product, but with the endo product being preferred. The transition structures for the two possible routes are determined below.
Exo Transition state
The same method as in part 2 was employed i.e optimize to a TS(Berny). The cycloehxadiene ring was manually adjusted so that it resembled a boat conformation, as otherwise the calculation failed due to too many steric interactions between it and the maleic anhydride. The resulting structure for the exo TS can be seen below along with its imaginary vibration of -812 cm-1 which corresponds to the TS. The energy of this TS is -0.05042 a.u.
 |
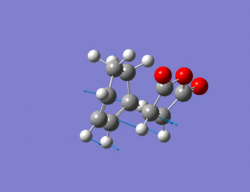 |
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.EXO_TS_6.LOG
Molecular orbitals:
 |
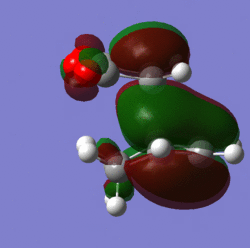 |
The new bond forming distance is 2.17 angstroms, the C=C bonds are 1.39 angstroms and the C-C bonds are 1.49 angstroms in length. The distance between the anhydride part of maleic anhydride and the CH2-CH2 fragment is 2.94 angstroms.
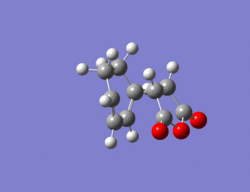
Endo Transition State
The same method as in part 2 was employed i.e optimize to a TS(Berny). The resulting structure for the endo TS can be seen below along with its imaginary vibration of -807 cm-1 which corresponds to the TS. The energy of this TS is -0.05150 a.u, therefore lower in energy than the exo transition state.
 |
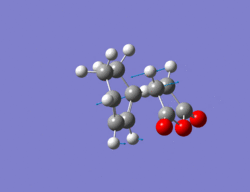 |
Output file: https://www.ch.ic.ac.uk/wiki/index.php/Image:Lo.ENDO_TS_6.LOG
Molecular orbitals:
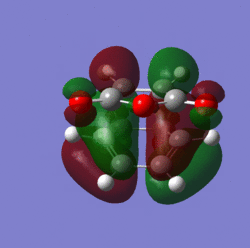 |
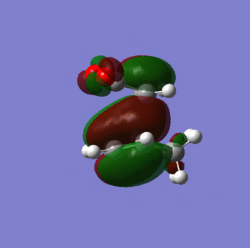 |
The distance of the new bonds being formed in the transition state is 2.16 angstroms. The C=C bond is 1.39 angstroms and the C-C bond is 1.49 angstroms in length. The distance between the anhydride fragment of maleic anhydride and the CH=CH fragment is 2.9 angstroms.
Comparison of Transition states
The endo transition state is lower in energy when compared to the exo transition state and this is due to two main reasons. The first reason is due to the the steric interaction between the anhydride fragment and the CH2-CH2 fragment of the cyclohexadiene ring, as shown below, which the endo form does not suffer from.

The other reason is due to secondary orbital overlap in the endo transition state. This seconadary overlap occurs between the LUMO of the maleic anhydride and the HOMO of the cyclohexa-1,3-diene. This stabilization is relatively small though, as is the steric interaction noted earlier which is why the two transition states are very close in energy. The endo transition state is more stable in this investigation and the endo product which results is in fact the kinetic product, as the activation energy required to form it is lower.
References
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ R. C. Smoot, R. G. Smith, J. Price, Merrill Chemistry, 1999, 316. ISBN 978-0-028-25527-9
