Rep:Mod3:lm709
Cope rearrangement
Optimising anti and gauche isomers (parts a and b)
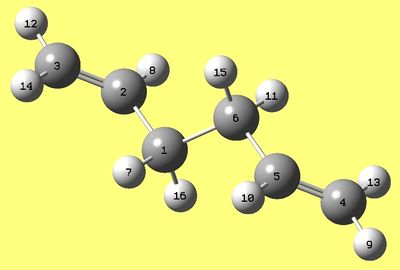
1,5- hexadiene in antiperiplanar conformation between carbons 3(C) and 4(C) was optimised using HF/3-21G method, then the same was done with a conformer which is gauche in between those carbons. Results are presented below:
| Model |  |
|
| Energy (a.u.) | -231.69097055 | -231.69266122 |
| Point group | Ci | C1 |
| Dipole moment (Debye) | 0.2957 | 0.3404 |
| RMS gradient (a.u.) | 0.00001285 | 0.00000667 |
| Link | DOI:/10042/to-11048 | DOI:/10042/to-11069 |
Lowest energy conformer
My previous calculations showed that gauche is more stable than anti, however there might be another anti that is more stable than some other gauche, therefore telling generally that in this case gauche is more stable than anti is not reliable, since it also depends on the method of calculation. Therefore we do not have enough of results even to start our argument about which is more stable. Therefore ideally we should calculate energies of all the conformers and even then their relative energies would differ depending on the method used. Since we are asked explicitly to calculate activation energies based on the structures generated with DFT/B3Lyp/6-31G* method, I will calculate conformers using the same method.
Three lowest energy anti structures and their energies (the most stable highlighted):
| Model |
|
|
| |||||||||
| Symmetry | Ci | C2 | C1 | |||||||||
| Energy (a.u.) | -234.61170275 | -234.61179048 | -234.61078875 | |||||||||
| Authenticity | DOI:/10042/to-11089 | DOI:/10042/to-11462 | DOI:/10042/to-11468 |
The same procedure was executed on gauche conformers and the three lowest in energy are presented below:
| Model |
|
|
| |||||||||
| Symmetry | C1 | C2 | C2 | |||||||||
| Energy (a.u.) | -234.61132934 | -234.61051916 | -234.61068500 | |||||||||
| Authenticity | DOI:/10042/to-11471 | DOI:/10042/to-11488 | DOI:/10042/to-11495 |
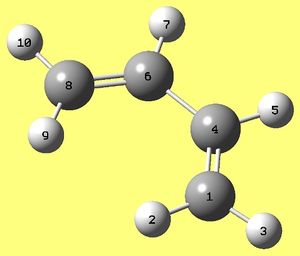
Anti Ci Hexadiene (part e)
As required Anti conformer with Ci symmetry was optimised using HF/3-21G theory and the following results were obtained:
| Model | 
|
| Energy (a.u.) | -231.69253518 |
| Point group | Ci |
| Dipole moment (Debye) | 0.0000 |
| RMS gradient (a.u.) | 0.00003489 |
| Link | DOI:/10042/to-11072 |
My version has the same point group, although is is a little higher in energy: the one in refference page has E= -231.69260, while mine has E= -231.69254, thus it is 0.00006 a.u. higher in energy, which is 0.158 kJ mol-1.
Then this optimised structure was further refined using a different method: DFT/B3LYP 6-31G(D) to get a more stable conformer, which is presented below:
| Model | 
|
| Energy (a.u.) | -234.61170275 |
| Point group | Ci |
| Dipole moment (Debye) | 0.0000 |
| RMS gradient (a.u.) | 0.00001330 |
| Link | DOI:/10042/to-11089 |
The difference in energies between two methods used is substantial, more precisely ΔE=234.61170275-231.69253518=2.91916757 (a.u.)In kilo calories that is ΔE=2.91916757 (a.u.)×4.3597×10-18(J a.u.-1)×6.0221×1023mol-1=7 664.1 kJmol-1. That is way higher than bond energies! Thus DFT/B3Lyp/6-31G* gives more stable structure of hexadiene.
Geometrywise we can compare bondlengths and dihedral angles of this molecule optimised at two levels of theory:
| Dihedral angles | Bondlengths |
|---|---|
| C(3)-C(2)-C(1)-C(6)=114.6
C(2)-C(1)-C(6)-C(5)=180.0 C(1)-C(6)-C(4)-C(4)=114.6 |
C(3)-C(2)=1.32
C(2)-C(1)=1.51 C(1)-C(6)=1.55 C(6)-C(5)=1.51 C(5)-C(4)=1.32 |
| Dihedral angles | Bondlengths |
|---|---|
| C(3)-C(2)-C(1)-C(6)=118.5
C(2)-C(1)-C(6)-C(5)=180.0 C(1)-C(6)-C(4)-C(4)=118.5 |
C(3)-C(2)=1.33
C(2)-C(1)=1.50 C(1)-C(6)=1.55 C(6)-C(5)=1.50 C(5)-C(4)=1.33 |
For the more stable conformer frequency prediction was run DOI:/10042/to-11230 to confirm it being at energy minimum. 42 modes were observed as expected (3×16−6=42). No negative frequencies appeared, the lowest being at 73 and 80 cm-1 representing the whole skeleton scissoring around central C-C bond. Resulting IR spectrum is given below:
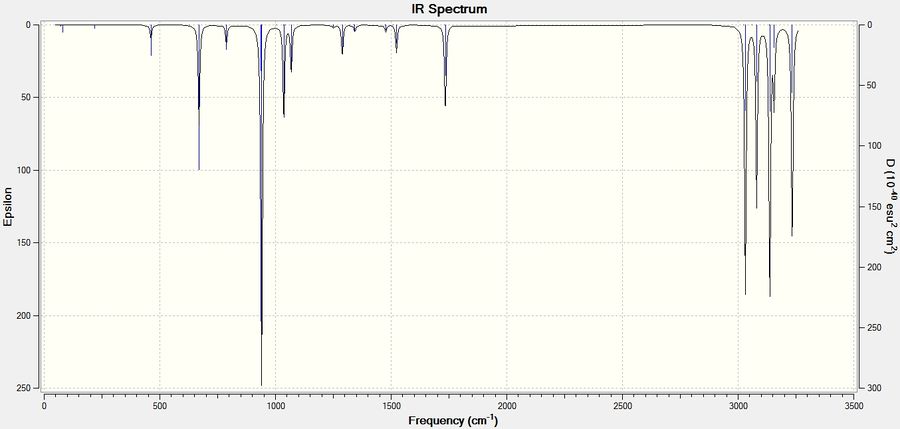
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Transition states
As we are investigating possible transition states in Cope rearrangement, it is necessary to optimise both transition structures to be able to compare their energies, symmetry and other relevant parameters. This was done by first completing calculations at HF/3-21G level of theory and then repeated at B3Lyp/6-31G*. Detailed description of all the procedures is given in the following two subsections. Since both transition states involve allylic fragment, the latter is optimised using both methods mentioned:
| Method | HF/ 3-21G | DFT/B3Lyp/6-31G* |
| Energy (a.u.) | -115.82303997 | -117.26035415 |
| RMS gradient (a.u.) | 0.00007225 | 0.00001572 |
| Model | 
Both C-C are 1.39 Å and angle between them = 124.3° |

Again both C-C are 1.39 Å, yet now angle between them = 125.1° |
| Authenticity | DOI:/10042/to-11144 | DOI:/10042/to-11145 |
As we can see both calculations converged giving vewry similar geometries, yet energy difference between two levels of theory is ΔE = 117.26035415 - 115.8230399 = 1.43731418 a.u. , which is 4.3597439422×10-18 (a.u. J-1) × 1.43731418 (a.u.) × 6.023 × 1023 = 3.77 kJ mol-1 (DFT / B3Lyp / 6-31G* being lower in energy as one can expect better estimate with more complete basis set).
Chair TS
This six-membered cyclic transition state involves two allyl fragments positioned about 2 angstroms apart (in C2h symmetry) and while they are interacting, TS reminds chair conformation cyclohexane ring (see figure 1).
We can use several methods to calculate transition structure and its energy, the ones used for chair transition state are: calculation of force constants and using redundant coordinates. As before both methods were calculated at two levels of theory (HF/3-21G and DFT/B3Lyp/6-31G*) using corresponding optimised allyl fragments.
The first optimisation was run by manually alligning two allyl fragments parallel and setting OPT+FREQ task with additional comand line "Opt=NoEigen". Results of this method are presented below:
| Method | Energy (a.u.) | RMS gradient (a.u.) | Frequency v (cm-1) | Model | C-C between
allyl units (Å) |
Authenticity | |||
| HF/3-21G | -231.61932223 | 0.00006145 | -818 |
|
2.02 | DOI:/10042/to-11146 | |||
| DFT/B3Lyp/6-31G* | -234.55698287 | 0.00003541 | -566 |
|
1.97 | DOI:/10042/to-11160 |
Vibration |
Now the same transition structure is modeled using frozen coordinate method. Input structures with two allyl fragments on top of each other were used as in a previously, although the whole structure had to be symmetrised (otherwise calculation failed to converge). For both theory levels first the fixed 2.2 angstrom distance between allyl end-carbon fragments was kept, which was later let vary to achieve optimal energy. Results are shown below, but this time without vibrational animation, since it was identical:
| Method | Energy (a.u.) | RMS gradient (a.u.) | Frequency v (cm-1) | C-C between
allyl units (Å) |
Authenticity |
| HF/3-21G | -231.61932199 | 0.00005433 | -818 | 2.02 | DOI:/10042/to-11188 |
| DFT/B3Lyp/6-31G* | -234.55693177 | 0.00004448 | -569 | 1.97 | DOI:/10042/to-11198 |
As we can see all optimisations converged and gave the same corresponding energy values as the ones above where frozen coordinate method was not employed. Vibrational frequencies of TS were also replicated.
Finally IRS calculation warun using the same method and only for thwe forward dirrection to give the following results (HF method):
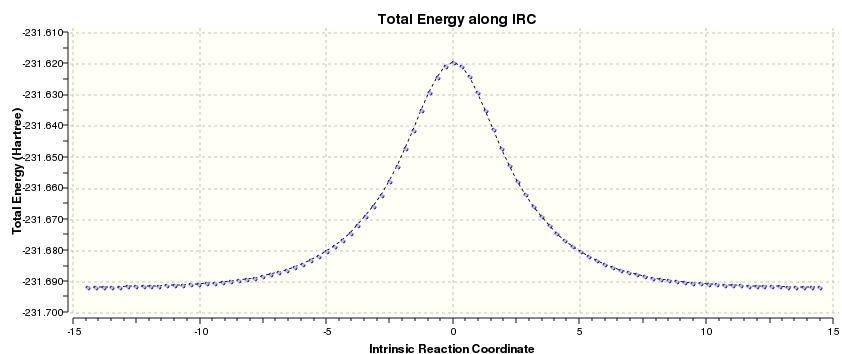
But even without running IRC we can tell that transition state starts and finishes with gauche conformer (C2 ) if we look at it from the top:

Boat TS
It is also possible that cope rearrangement occurs via boat transition state, which we are going to optimise in this section using both levels of theory as before. Although now a different method was employed. Synchronous Transit-Guided Quasi Newton (QST2) method requires reactant and product structures as an input and they should have their conformations close to transition structure. Anti conformer of 1,5- Hexadiene (Ci symmetry), which was optimised earlier on was used as an input. Results of optimised TS models are given below:
| Method | Energy (a.u.) | RMS gradient (a.u.) | Frequency v (cm-1) | C-C between
end carbons (Å) || Model |
Authenticity | ||||
| HF/3-21G | -231.60280146 | 0.00016481 | -839 | 2.14 |
|
DOI:/10042/to-11207 | |||
| DFT/B3Lyp/6-31G* | -234.54309301 | 0.00003744 | -530 | 2.21 |
|
DOI:/10042/to-11208 |
Vibration |
Finally IRC calculation of boat TS was modeled (HF method):
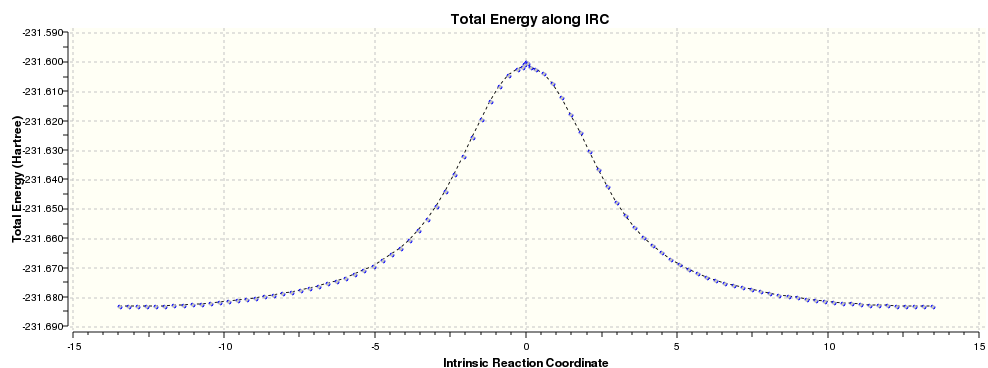
Activation Energies
Now we can calculate Activation energies for boat and chair transition states using results from DFT/B3Lyp/6-31G* calculations of 1,4-hexadiene (anti conformer C2 symmetry)and both transition structures. Therefore for the Chair TS:
Ea= ΔE = 234.55698287 - 234.61179048 = 0.05480761 a.u.
Ea=0.05480761 a.u.×4.3597×10-18(J a.u.-1)×6.0221×1023mol-1= 144 kJ mol-1
Alternatively: Ea= 34.4 kcal mol-1
For the boat TS activation energy was:
Ea= ΔE = 234.54309301 - 234.61179048 = 0.06869747 a.u.
Ea=0.06869747 a.u.×4.3597×10-18(J a.u.-1)×6.0221×1023mol-1= 180 kJ mol-1
Alternatively: Ea= 43.0 kcal mol-1
Diels-Alder reaction
In this section we are going to emplyed previously used techniques to study two Diels-Alder type pericyclic cycloaddition reactions. The first one is between 1,3-butadiene and ethylene, which explores molecular orbital symetry involved and the second is between maleic anhydride/1,3-cyclohexadiene, which involves secondary orbital interaction analysis.
Butadiene + Ethylene
Reaction under investigation is between ethylene and 1,3-butadiene to give cyclohexene:
Cycloaddition proceeds thermally, thus we consider ground state HOMO-LUMO region of both reactants. There are two possible combinations of HOMO/LUMO pairs that give the right symmetry for overlap. It can be HOMO of butadiene (a) and LUMO of ethene (a) reacting:
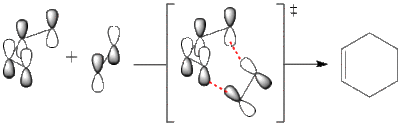
Alternatively it can be LUMO of butadiene (s) and HOMO of ethene (s) reacting:
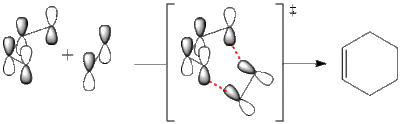
To determine which is the correct scenario we need to model the transition state structure and take a look at its HOMO, thus first s-cis butadiene optimisation was done at DFT/B3Lyp/6-31G* level of theory and gave the following results:
As we can easily predict the shape of conjugated π MO's in polyenes using Hückel method of linear combination of π AO's, linear combination of two ethylene units gives us butadiene MO's (LCAO fashin):
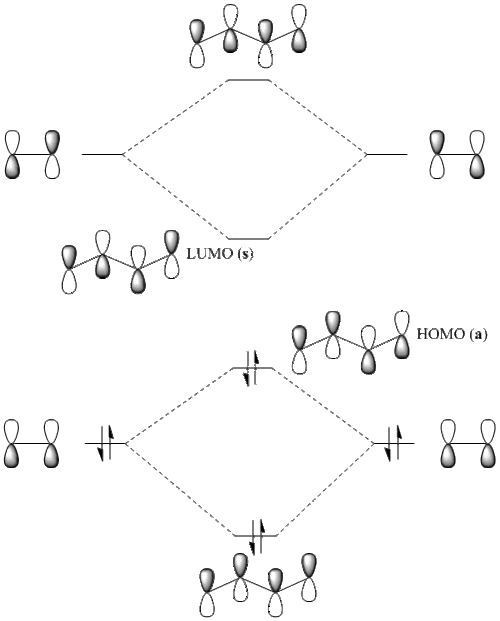
The actual MO's of butadiene (shown below) confirm all the qualitative features of LCAO Hückel method:
| HOMO | LUMO | |
|---|---|---|
| Picture |  |
|
| Symmetry | a | s |
Transition state calculation
For this step butadiene and ethylene were preoptimised and then transition state optimised using two levels of theory as before (HF/3-21G and DFT/6-31G*)resuls are summarised below:
| Method | Energy (a.u.) | RMS gradient (a.u.) | Frequency v (cm-1) | Model | C-C between
end carbons (Å) |
Authenticity | |||
| HF/3-21G | -231.60320857 | 0.00000490 | -818 |
|
2.21 | DOI:/10042/to-11292 | |||
| DFT/B3Lyp/6-31G* | -234.54389655 | 0.00000461 | -525 |
|
2.27 | DOI:/10042/to-11274 |
Vibration |
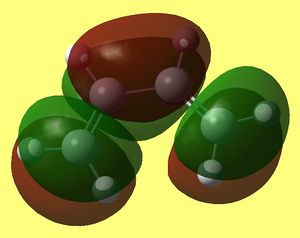
Some geometrical features of DFT/B3Lyp?6-31G* optimised Transition State (higher level calculation than HF...) have to be noted here. First, the angle at which those two molecules interact. they are not approaching one another in "bottom/top fashion" but rather at an angle, which is 12.3° (since we define contact angle as an angle that an object makes to the normal of the surface of interest - butadiene in this case: thus 102.3° - 90° = 12.3°):
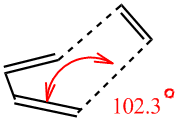
In the transition state separation between interacting carbon atoms is about 2.2 angstroms, which is higher than for a typical C-C sp3 bond (1.54 A average) or C=C sp2 (1.47 angstroms)[1]. This indicates interaction that is not a bond yet. Van der Waals radius for carbon is 1.6 angstroms so two carbons interact favourably strongest when they are 3.2 angstroms apart (longer than our TS distances).
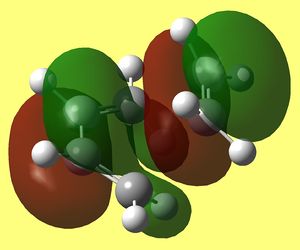
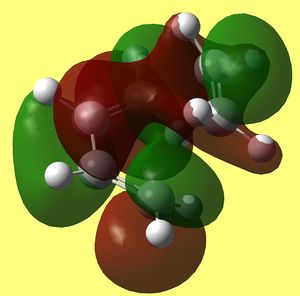
Now that transition structure was found and optimised at two levels of theory and that the only imaginary frequency corresponds to the formation of two sigma bonds between both ends of alkene and diene, we can examine its Frontier orbitals. Resulting HOMO HOMO -1 and LUMO that were generated at DFT/B3Lyp/6-31G* level are shown below:
| Model | 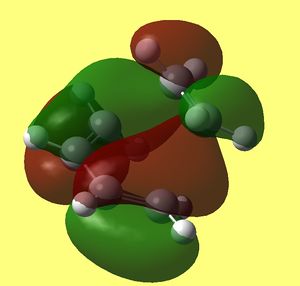
HOMO - 1 |
HOMO |
LUMO |
| Symmetry | a | s | s |
| Relative energy (a.u.) | -0.22107 | -0.21897 | -0.00862 |
We know that some orbitals are very close in energy and calculations some times do give the wrong ordering, therefore in my results above I included HOMO - 1 MO. In the transition structure we expected to be able to see how Frontier orbitals of both reagents interact by inspecting its MO's. Naturally, butadiene should maintain characteristic features of its pi MO's that were ilustrated (MO's of butadiene below its modeled structure), which includes pi electron density on all carbons. However we can not see this in HOMO of TS, but very close to it we have HOMO-1, that has them, therefore it will be analysed instead and denoted HOMO*.
HOMO* is antisymmetric to the plane bisecting C=C of alkene and C-C of butadiene and it looks exactly like HOMO of butadiene molecule overlaping with LUMO of ethylene molecule in progress (since lobes that mach the sign are coming together through space and fusing into one - forming two C-C sigma bonds at both ends of diene and alkene). Since this one is lower in energy than LUMO of TS, it is likely the path that is taking place in this cycloaddition, which concludes that HOMO os butadiene is reacting with LUMO of ethylene.
On the other hand LUMO of TS illustrates LUMO of butadiene interacting with HOMO of ethene. However we see that now bonding π MO of ethene is interacting with the lobe of the same sign in diene but at the back of it instead of the ends, where it is supposed to form bonds. This interaction would not lead to cyclohexene formation.
Regioselectivity
Cyclohexadiene and maleic anhydride undergo thermal [4 +2] cycloaddition and there are two possible products in this reaction:
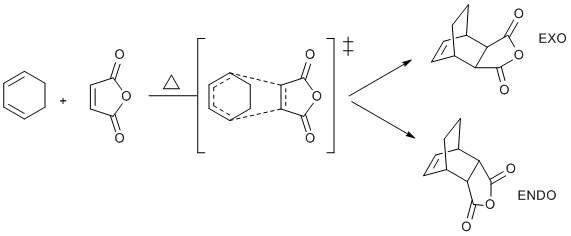
Experimental results show a great tendency towards endo product, eventhough exo one is thermodynamically more stable (also confirmed in computational lab I). Therefore it means that endo product transition state has smaller ΔG‡, which means it is more stable. The aim of this section is to investigate this phenomenon and look at the reasons behing it. To do this both endo and exo TS's were optimised at two levels of theory (HF/3-21G and DFT/B3Lyp/6-31G* as in previous parts) and results compared.
Endo TS
Results for endo TS are given below:
| HF | DFT | |||||||
|---|---|---|---|---|---|---|---|---|
| Energy (a.u.) | -605.60716923 | -612.68339679 | ||||||
| RMS gradient (a.u.) | 0.00313908 | 0.00001306 | ||||||
| frequency (cm-1) | -666 | -447 | ||||||
| Reacting C-C distance (Å) | 2.17, 2.25 | 2.27 | ||||||
|
| |||||||
| Authenticity | DOI:/10042/to-11317 | DOI:/10042/to-11333 |
Vibrational mode corresponding to the imaginary frequency and that leads to pericyclic reaction is illustrated below together with selected all bondlengths of DFT/B3Lyp/6-31G optimised structure:

|
|
| Bond | Bondlength (Å) |
| C(6)-H(12) | 1.09 |
| C(17)-H(20) | 1.08 |
| C(18)-O(21) | 1.40 |
| C(17)-C(18) | 1.48 |
| C(16)-H(19) | 1.08 |
| C(16)-C(17) | 1.39 |
| C(15)-O(22) | 1.20 |
| C(15)-O(21) | 1.40 |
| C(15)-C(16) | 1.48 |
| C(18)-O(23) | 1.20 |
| C(5)-H(11) | 1.09 |
| C(5)-C(6) | 1.39 |
| C(4)-H(13) | 1.10 |
| C(4)-H(10) | 1.10 |
| C(4)-C(5) | 1.52 |
| C(3)-H(14) | 1.10 |
| C(3)-H(9) | 1.10 |
| C(3)-C(4) | 1.56 |
| C(2)-H(8) | 1.09 |
| C(2)-C(3) | 1.52 |
| C(1)-H(7) | 1.09 |
| C(1)-C(6) | 1.40 |
| C(1)-C(2) | 1.39 |
Again we can see that interaction distances between carbons 5/17 and 2/16 (both 2.27 angstroms) are longer than either single or double C-C bond elsewhere in those molecules, which indicates bond being formed, but not quite formed yet. Other important distances between both reactant molecules include C-C between rings (6/18 and 1/15 both equal to 3.00 Å). This means that only four carbons come closest together in this TS and hydrogens in -CH-CH- are in the ring plane and do not clash with maleic andydride, this being steriically favourable as well. Now let's take a look at HOMO of this transition state:
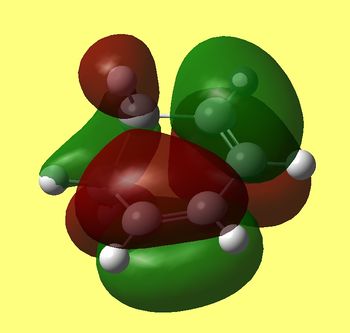
HOMO of cyclohexadiene |
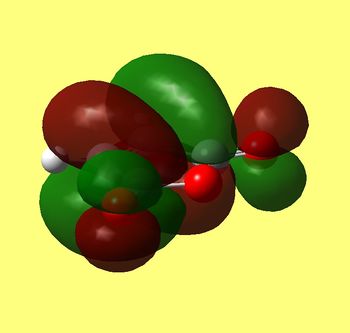
LUMO of maleic anhydride |
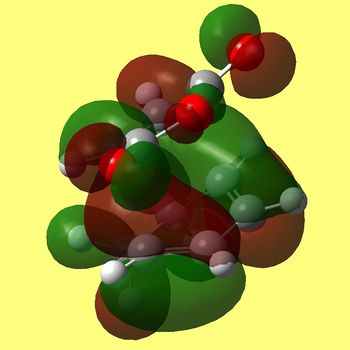
HOMO of Transition State |
Clearly HOMO of this TS is antisymmetric (as well as HOMO of diene and LUMO of alkene) and we can see in phase overlap of diene/maleic anhydride MO's to form sigma bonds between corresponding carbon atoms (17/5 and 16/2). Although we can also see that lobes that overlap in diene and anhydride extend through two carbon atoms and therefore interact in phase not only to bond (17/5 and 16/2) but also keep (6/18 and 1/15) together. This extra stabilisation lowers TS in energy and is therefore kinetically preferred reaction route. As in the previous section electron rich diene's HOMO overlaps with dienophile's LUMO, which are both antisymmetric and TS HOMO is antisymmetric too (with respect to the plane). We can also spot small lobes on oxygen in TS's HOMO that are in phase with large lobes underneath, which is if not significantly favourable, at least not disfavourable interaction.
Exo TS
Exo Transition State was also optimised using two levels of theory as before:
| HF | DFT | |||||||
|---|---|---|---|---|---|---|---|---|
| Energy (a.u.) | -605.60263136 | -612.67931096 | ||||||
| RMS gradient (a.u.) | 0.00298882 | 0.00000131 | ||||||
| frequency (cm-1) | -628 | -449 | ||||||
| Reacting C-C distance (Å) | 2.25, 2.29 | 2.29 | ||||||
|
| |||||||
| Authenticity | DOI:/10042/to-11332 | DOI:/10042/to-11350 |
Initially TS was optimised running HF method and the resulting structure reoptimised using DFT code. It made the resulting structure more symmetric :maleic anhydride now sits parallel to cyclohexadiene and both C-C interaction distances are equal to 2.29 Å. The detailed bondlength summary will be given below together with the animation of vibrational mode that leads to product formation (v = -449 cm-1 in DFT method).
| _ | 
|
|
Exo TS, however is more sterically demanding than endo, since now maleic anhydride approaches -CH2-CH2- unit instead of -CH=CH-, therefore hydrogens are sticking out of cyclohexadiene ring and poling into anhydride's. These are the following relevant distances: C(1)/C(13) and C(6)/C(16) are 3.03 Å (similar to analogous in endo structure), although now two methylene hydrogens come much closer (2.53 Å) to those carbons C(13)/H(7) and C(16)/H(12) nearly as close as two pairs of carbons (C(13)/C(2) and C(16)/C(5)). Again about C-C Van der Waals radii, distance between interacting (bond producing) carbons is 2.29 Å, which is less then twice carbon's VdW radius - 3.2 Å, which means that they are pushed together towards each other from their comfortable sitting positions, which causes rise in energy, which reaches maximum at TS.
| C(18)-O(23) | 1.20 |
| C(18)-O(21) | 1.40 |
| C(17)-H(20) | 1.08 |
| C(17)-C(18) | 1.48 |
| C(16)-H(19) | 1.08 |
| C(16)-C(17) | 1.40 |
| C(15)-O(22) | 1.20 |
| C(15)-O(21) | 1.40 |
| C(15)-C(16) | 1.48 |
| C(6)-H(13) | 1.10 |
| C(6)-H(12) | 1.09 |
| C(5)-H(11) | 1.09 |
| C(5)-C(6) | 1.51 |
| C(4)-H(10) | 1.09 |
| C(4)-C(5) | 1.39 |
| C(3)-H(9) | 1.09 |
| C(3)-C(4) | 1.40 |
| C(Z2)-H(8) | 1.09 |
| C(2)-C(3) | 1.39 |
| C(1)-H(14) | 1.10 |
| C(1)-H(7) | 1.09 |
| C(1)-C(6) | 1.56 |
| C(1)-C(2) | 1.51 |
As before HOMO of TS was generated to investigate possible secondary orbital overlap in this transition state:
| Orbital | 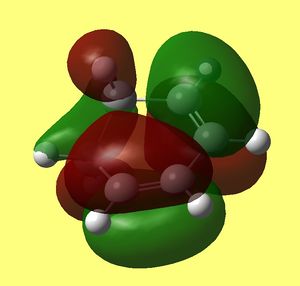
HOMO of cyclohexadiene |
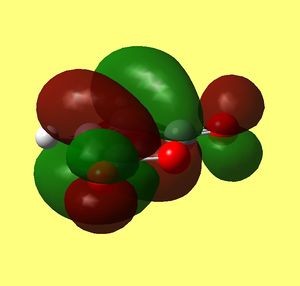
LUMO of maleic anhydride |
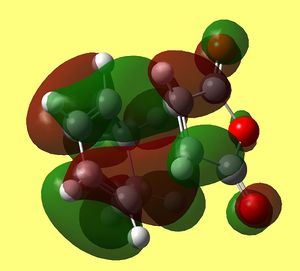 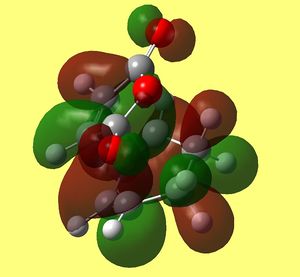
HOMO of Exo Transition state back and front sides |
| Symmetry | a | a | a |
As in previous cases HOMO of transition state is a result of overlap between HOMO of diene and LUMO of maleic anhydride (dienophile). Clearly the lobes involving carbons (C(15)/C(5) and C(14)/C(2)) that are forming sigma bond overlap in phase and fully (you can see them fused in the upper picture). however now the orientation does not allow any interaction of carbons on maleic anhydride ring (C(16) and C(13)) to any π character lobes on cyclohexadiene ring. The only in phase interaction would be between oxygen lone pairs (both carbonyls) and lobes on methylene hydrogens pointing towards them. Yet they are far apart and not giving overlap.
Endo vs Exo
It has been briefly described how endo transition state differ from exo, which is primarily due to secondary orbital overlap and sterical reasons. So we have seen that sepsration between reacting carbon atoms in both structures is about the same: 2.27 Å for Endo and 2.29 Å for Exo (results from DFT/B3Lyp/6-31G* calculations, which will be referred to throughout the discussion, since it is a higher level of theory). However in endo product both reagents are planar in transition state site, thus the closest they approach is at two pairs of carbons that later connect, whereas in exo TS besides these pairs of carbons we now have methylene groups at the back of TS carbon framework and two H's point towards the inside of the envelope shape of TS, thus imposing a sterical demand to accommodate them there:
| Endo | Exo | ||||||
|---|---|---|---|---|---|---|---|
|
|
Inside the envelope we have 2.53 Å for Exo between carbonyl carbon and methylene H and 3.14 Å between the same carbon and now H from -CH=CH- (greater separation in endo - less sterical demand), which illustrates the previous claim. There is also a favourable H---H Van der Waals interaction between hydrogens of maleic anhydride and cyclohexadiene's methylene group, that are separated by 2.35 Å (2.4 is ideal for maximum interaction and , 2.1 it becomes repulsive) in Endo TS, that further stabilises it. Contrary to this, in Exo TS the corresponding H's at the back of the envelope (H from maleic anhydride and H from =CH-CH= are 3.03 Å that gives no effective interaction. There is also another pair of H's in both Endo and Exo TS's on the side of the structure and they are separated by 2.63 Å and 2.63 Å respectively that might give some little favourable interaction too, yet as mentioned they exist in both TS's and do not effect their relative energy difference.
Another major aspect controling relative TS energy is secondary overlap effect that is present in Endo TS as illustrated and discussed above. This makes it lower in energy alongside with all the favourable steric effect just discussed and therefore we observe the kinetic control of this reaction giving the predicted endo product.
- ↑ Secon year Organic Chemistry material: Henry Rzepa "Conformational analysis"