Rep:Mod3:letsgetphysical
Module 3: Physical- The Transition State
The Cope Rearrangement
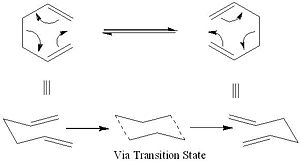
The Cope Rearrangement, originally developed by Arthur C. Cope, is the general name given to an organic reaction involving a [3,3]-sigmatropic rearrangement of 1,5-dienes. Although it has been heavily debated that the Cope Rearrangement goes via a two-stage diradical intermediate, it is now accepted that the rearrangement is a concerted and pericyclic reaction via the chair configuration (shown in the example) or the boat configuration [1]. The boat configuration however, is considerably higher in energy. The Cope Rearrangement shown has been studied extensively and is of great interest to computational chemists as the reaction profile, for the rearrangement, is symmetric. Therefore, it is only necessary to know information about one of the reactants or products to understand the reaction pathway to and from the transition state.
In this section of the report the aim is to locate the low-energy minima and the transition structures of the C6H10 molecule and to determine the preferred reaction mechanism.
Optimising The Reactants and Products
As 1,5-dienes have free rotation about the three central C-C bonds, which are three of the 5 total C-C bonds, there are very many different conformations of this molecule. The most stable of these conformations are when, if you were to look straight down the central C-C bond, the two C2H3 groups/alkene groups are antiperiplanar or gauche with respect to each other. The table provided in appendix one summarises the many conformations of 1,5-hexadiene to the 10 most stable conformations.
Some of the structures shown in appendix 1 will be recreated using Gausview and then their energies and point groups can be established.
a) As a starting point a molecule of 1,5-hexadiene was modelled in Gausview so that there was an antiperiplanar relationship along the central C-C bond. The structure was then 'Cleaned' using the appropriate function in Gausview. The starting structure for the optimisation of 1,5-haxadiene is given below;
 |
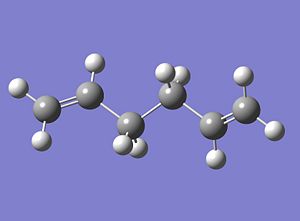The code for the optimisation of the 1,5-hexadiene starting structure is given below;
# opt hf/3-21g geom=connectivity Anti_1,5-Hexadiene
Log File: https://www.ch.ic.ac.uk/wiki/images/8/86/ANTI_15HEXADIENE.LOG
The first optimised structure of 1,5-hexadiene is shown below;
.jpg) |
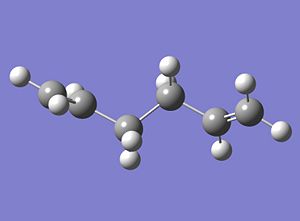The Energy of the structure was calculated to be -231.69260 Hartree and the Point group was found, using the symmetrise function on Gausview, as C2. When comparing this structure with those displayed in 'Appendix 1' it can be concluded that the 'anti1' structure has been formed.
b) Using Gausview, a second structure of the 1,5-diene was drawn. This time the dihedral angles between the groups on each C-C bond were manually altered so to have a gauche linkage between the central 4 carbon atoms. This structure was then optimised and the codes for the optimisation are stated below;
# opt hf/3-21g geom=connectivity Gauche_1,5-hexadiene
Log File:https://www.ch.ic.ac.uk/wiki/images/9/94/GAUCHE_15HEXADIENE.LOG
The Optimised gauche structure is given below;
 |
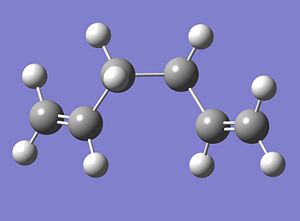The energy of this structure was calculated to be -231.691530 Hartree and the point group is C2. This is an unexpected result as the energy is lower than that of the anti1 conformer. It would be expected that the first optimised structure, where the C-C bonds had an antiperiplanar relationship would be the most stable as the bulky C2H3 groups are angled so that they as far away from each other as possible (180o) thus minimising the steric clash experienced between the two groups. The second structure, where the C-C bond show a gauche relationship between the two C2H3 groups would be expected to have a higher energy/be less stable as the angle between the two bulky groups has been reduced to 60o in this conformation and so the steric clash between these two groups should be larger that of the anti case. As this unexpected result cannot be rationalized through steric reasoning it must be concluded that the gauche conformation is stabilised by an electronic interaction which cannot be recognised by simply modelling the structures in 3D and calculating their energies.
c) It was then to be investigated as to which conformation of 1,5-haxadiene has the lowest overall energy and is therefore the most stable. From a steric point of view it would be predicted that the lowest energy conformation would have an antiperplanar relationship along each of the three central C-C bonds within the molecule. This prediction was tested by modelling the molecule in Gausview and then optimising its structure.
The codes for the optimisation of the all anti diene is;
# opt hf/3-21g geom=connectivity anti(allanti)_1,5-hexadiene
Log File: https://www.ch.ic.ac.uk/wiki/images/2/2b/ANTI%28ALLANTI%29_15HEXADIENE.LOG
The optimised structure is shown below;
_15cyclohexadiene.jpg) |
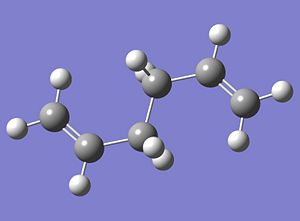The calculated energy of the structure was -231.689070 Hartree and it was found to have C2h point group symmetry. Although this structure is more stable than the two analysed above it cannot be assumed to be the most stable structure. As has been proved with the two molecules described above, steric effects are not the only interactions determining the stability of the structure, there may also be some electronic effects that need to be considered. Therefore, in attempt to find the conformation with the lowest overall energy a compromise between these two effects was made. A structure with one of the C2H3 groups adopting an anti conformation and the other adopting a gauche conformation was drawn in Gausview. The structure was then optimised and the corresponding optimisation codes are given below;
# opt hf/3-21g geom=connectivity anti/gauche_1,5hexadiene
Log File:https://www.ch.ic.ac.uk/wiki/index.php/Image:ANTI%28MOSTSTABLE%29_15HEXADIENE.LOG The optimised structure is given below;
.jpg) |
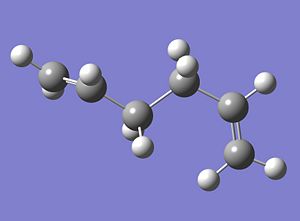The calculated energy of this structure is -231.610788 Hartree. As this structure is lower in energy than that where the all the central C-C bonds adopt an antiperiplanar conformation it is predicted that a combination of anti and gauche gives the most stable conformation of the 1,5-hexadiene molecule. However, on consulting the table displaying the 10 most stable conformations of 1,5-hexadiene, it is clear that the prediction made above is in fact incorrect. The most stable conformation (conformer 4) has an all gauche orientation about all three of the central C-C bonds. Conformer 5 was therefore modelled using Gausview and the structure was optimised.
# opt hf/3-21g geom=connectivity pop=full Gauche_conformer5_opt
Log File; DOI:10042/to-4235
The optimised structure of conformer 5, the most stable conformation of 1,5-hexadiene is shown below:
 |
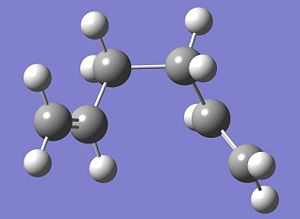d) The structures produced above and their corresponding energies can be compared with those depicted in 'appendix 1'. The following table does just that.
| Conformation | Energy / Hartree | Equivalent from Appendix 1 |
|---|---|---|
| 1 | -231.69260 | anti1 |
| 2 | -231.691530 | gauche4 |
| 3 | -231.689070 | anti2 |
| 4 | -231.690970 | anti4 |
| 5 | -231.692661 | gauche3 |
Theory and Discussion
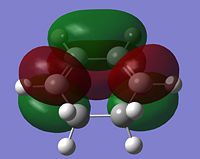
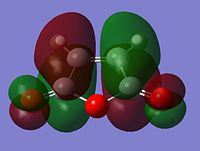
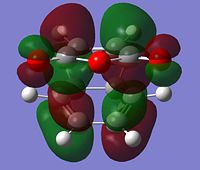
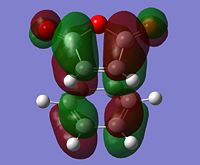
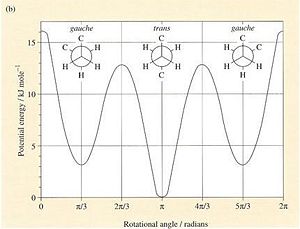
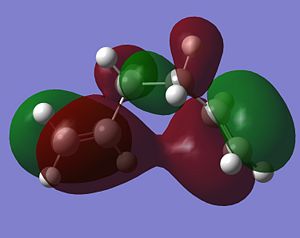
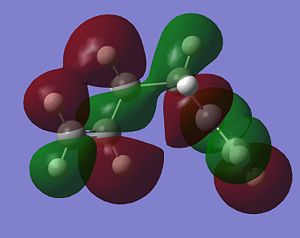
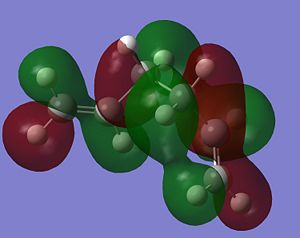
As stated above, the fact that the gauche conformation in conformer 2 is more stable than the antiperiplanar conformation in conformer 1 is a surprising result. This is because, in general, when there is rotation about C-C bonds, the bulky groups prefer to be anti to each other as then they are as far apart as possible from each other and so experience less destabilising steric interactions. The closer the two bulky groups become/the smaller the dihedral angle is between them, the less stable and the higher the energy of the structure. This reaches a maximum energy (or an extreme situation) when the dihedral angle between the bulky substituents is reduced to 0o and there is an eclipsed relationship between the two groups which gives rise to maximal steric clash. This is summarised in Figure 1 which shows the conformational analysis of butane [2]. As the gauche conformation was found to be the more stable, there must be a second set of interactions that are over-riding the steric destabilisation which are electronic interactions. It was therefore predicted that the most stable conformation of 1,5-hexadiene was conformer 4 which adopts a gauche interaction at one end of the molecule and an antiperiplanar interaction at the other end. It was predicted that this conformation would be a compromise between the destabilising steric interactions experienced by two bulky groups that are orientated relatively close to each other and the stabilising electronic interactions experienced when the C=C group adopts a gauche interaction. Electronic interactions can be visualised well using molecular orbitals. In the case of conformer 5, the most stable conformation of 1,5-hexadiene, there are very significant electronic interactions which are stabilising the molecule to such an extent that they compensate for the steric destabilisation previously described. The MO representations below depict pictorially the electronic stabilising interactions present in conformer 5:As can be seen in the MO representations below there is significant donation of electron density from the C-H sigma orbitals into the C=C pi* antibonding orbitals. These interactions are called hyperconjugation and as can be seen are bonding interactions and so are extremely stabilising.
 |
 |
 |
 |
 |
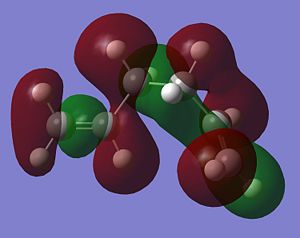There are two separate stabilising interactions that are opposing the destabilising steric interactions discussed previously. The first of these interactions is depicted in the MO representation of the HOMO where one can see a bonding interaction between the two pi bonds present in the molecule. This overlap of electron density increases in strength as the two double bonds become orientated closer together in space. However, this will also cause an increase in the destabilising steric interactions. The second electronic interaction which stabilises this conformation is shown in the MO representations of the HOMO-2,HOMO-3 and HOMO-5. As shown, there is an example of a bonding overlap of electron density in each representation between the sigma C-H MO and the antibonding pi* C=C MO. This interaction in termed hyperconjugation and has a stabilising effect on the overall conformation. These stabilising interactions are present in each gauche conformation of 1,5-hexadiene but to different extents. However, as already mentioned, an increase in these stabilising interactions (from having the two double bonds orientated closed to each other) is also accompanied with an increase in steric interactions which destabilise the whole molecule. Therefore, the gauche 3 conformation (conformer 5) is a compromise between these three interactions described and therefore has the lowest overall energy.
e) The structure of the anti2 conformer has already been located (analysis can be found above) and it corresponds to conformer 2 from the above table.
d) Now the structure with the minimum overall energy has been found it is necassary to re-optimise this structure using a more accurate basis set. This is done because basis sets of a low accuracy sometimes only give a rough representaion of what the lowest energy structure should actually be. Therefore, it is essential to check the structure even though in a lot of cases the geometry may not be significantly altered.
The codes for the second optimisation of conformer 5, using a better basis set, are given below;
# opt b3lyp/6-31g(d) geom=connectivity Gauche3_ReOPT_HighBS
Log File: DOI:10042/to-4236
The resulting geometry of the re-optimised conformation was no different to that depicted (above when a lower basis set was used). Therefore, it did not seem necessary to include a representation of it in the report. Therefore, in this case it can be concluded that the lower basis set gave an adequate representation of the conformation in terms of geometry. The energy of the conformer, however, did change dramatically. Using the B3LYP/6-31G method, the energy of conformer 4 was calculated to be -234.610789 Hartree. Therefore, the better basis set has calculated the energy of the conformer to be more stable by 210.515 kJ/mol. This implies that although the two different basis sets give the same representation of conformer 4 in terms of geometry, they do not calculate the energy to be the same. As the B3LYP/6-31G method is the most accuarate, it is assumbed that the energy calculated using this basis set is the more realistic of the two.
g) A frequncy analysis calculation is now to be performed on the optimised structure of conformer 4.
# freq b3lyp/6-31g(d) geom=connectivity Anti_MostStable_DFT_Freq
Log File: https://www.ch.ic.ac.uk/wiki/images/3/33/ANTIMOSTSTABLE_DFT_FREQ.LOG
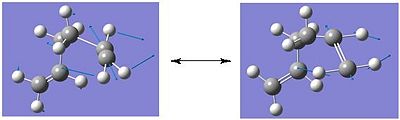
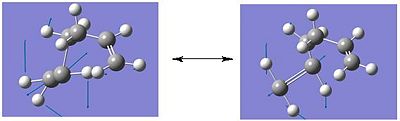
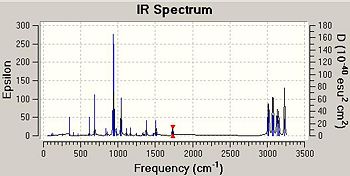
The frequency calculation is necessary in order to confirm that the minimal energy structure has in fact been obtained. This is checked by viewing the vibrations of the conformer, using Gausview, and checking there are no imaginary frequencies i.e. they are all positive. The vibrations of the C=C double bonds are represented below and the IR spectrum of the molecule is also shown. These frequencies correlate well with those stated for 1,3-butadiene in the literature; 1395 and 1376 cm-1 [3], therefore, it can be concluded that this method of computational chemistry gives accurate results in terms of frequency analysis.
| Vibration | Frequency | Description |
|---|---|---|
|
1731 | C=C bond on the right of the molecule is stretching and compressing |
|
1732 | C=C bond on the left of the molecule is stretching and compressing |
 |
In order to compare any results obtained computationally to those obtained empirically, additional thermochemistry data has to be calculated. The frequency calculation allows for this and the following pieces of data have been obtained for conformer 5:
| Thermochemistry Term | Energy / Hartree |
|---|---|
| Sum of electronic and zero point energies | -234.468693 |
| Sum of electronic and thermal energies | -234.461464 |
| Sum of electronic and thermal enthalpies | -234.460520 |
| Sum of electronic and thermal free energies | -234.500105 |
Optimising the Chair and Boat Transition Structures
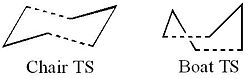
In this section the transition state of the Cope Rearrangement is to be analysed in detail. The transition state can adopt two different configurations; the chair or the boat (shown).
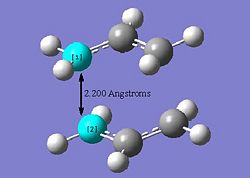
As a starting point, an allyl fragment C3H5 was modelled using Gausview. The two transition structures are essentially are two of these allyl fragments joined together by a 'partial bond' of approximately 2.2 Angstroms but oriented differently to give rise to different symmetry. The allyl fragment was then optimised using the HF/3-21G level of theory and the optimised structure is shown below. Therefore, half of the full transition state structures have now been obtained.
The optimised structure of the allyl fragment (half the full structure of the transition state) can then be used to facilitate the optimisation of the chair and boat transition structures.
The Chair Transition Structure
Optimisation calculations to find a transition state structure iare more complicated than normal minimisation calculations because the calculation needs to be provided with information about the negative curvature (or reaction coordinate) is located. In the case of the chair transition state, as it is already known what the structure should look like, an adequate guess of the final structure can be made (and modelled in Gausview) and then the force constant matrix (also known as the hessian) can be computed at the beginning of the calculation which will then get updated as the optimisation proceeds. In order to model the starting structure, for the chair transition state, in Gausview, the allyl fragment (previously optimised) was copied and then pasted twice into a new window. The two fragments were then orientated so that they resemble the chair transition state. The distance between the two terminal carbons on each fragment were altered to be 2.2 Angstroms. The codes for the 'guess' structure TS optimisation are given below;
# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity PartB_Chair_TS
Log File:https://www.ch.ic.ac.uk/wiki/images/9/9b/OPT_TS_GUESS.LOG
In a lot of cases it is very difficult to obtain an adequate enough 'guess' of the structure of the transition state in the input file. A better structure for the transition state can therefore be generated by firstly freezing the reaction coordinate and then secondly minimising the rest of the molecule (without altering the reaction coordinate). Once the optimisation of the rest of the molecule is complete, the reaction coordinate can then be unfrozen and then the optimisation of the transition state is continued.
# opt=modredundant hf/3-21g geom=connectivity PartC_TS_Chair_OPT
Log File:https://www.ch.ic.ac.uk/wiki/images/b/b9/PARTC_CHAIR_OPT.LOG
The resulting stucture from the above calculation looked identical to that obtained in part B. The difference between the two structures is simply that the bond lengths between the terminal carbons in the two allyl franments has been fixed to 2.2 Angstroms. Now these bond legths have been fixed, they can be submitted to optimisation also.
# irc=(forward,maxpoints=50,calcfc) rhf/3-21g scrf=check guess=tcheck geom=(modredundant,connectivity,allcheck) genchk PartD_TS_Chair_OPT
Log File:https://www.ch.ic.ac.uk/wiki/images/4/46/PARTD_CHAIR_OPT_COPY.LOG
 |
 |
 |
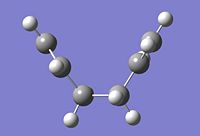
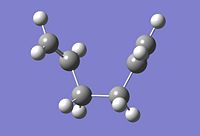
The Boat Transition Structure
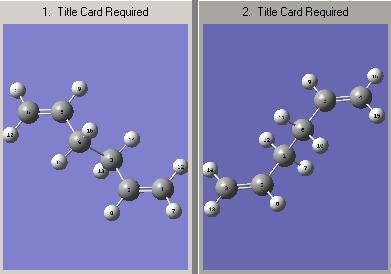
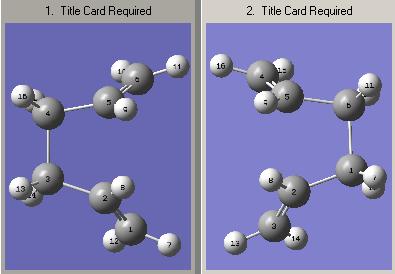
e) The boat transition state structure is to be optimised using a different method to what has been used previously. The QST2 method is to be used in which, the reactants and products can be specified and the reaction will then interpolate between these two structures in order to locate the transition state structure. The anti2 conformer, located in the first section of the report, was copied into a new Gausview window, this is going to be the reactant molecule. Then, using the 'Add to Molgroup' function a second anti2 molecule was copied into a separate window, this is going to be the product molecule. as both the reactant and product molecule is 1,5-hexadiene, it is necessary to number the atoms in a way which corresponds to the numbering obtained if the reactant had rearranged. The numbering for the reactant molecule (left) and the rearranged product molecule(right) is shown below.
Once the reactant and product molecules were numbered according the rearrangement reaction, the QST2 optimisation was set up to locate the associated transition state. The codes for the optimisation are given below:
# opt=(qst2,noeigen) freq hf/3-21g geom=connectivity PartE_QST2_OPT_TS
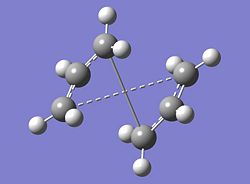
The calculation failed and the structure formed is shown. The correct structure was not ontained because when the calculated reaction interpolated between the reactant and product it did not consider possible rotations around the central C-C bond. In order to obtain the actual structure for the boat transition state manual alterations need to be made to the geometries of the reactants and products in the input file. Firstly, the central C-C-C-C dihedral angle was changed to 0o. Secondly, the inner C2-C3-C4 and C3-C4-C5 adgles were reduced to 100o. This process was repeated for both the reactant and product structures. The manually altered structures are shown below.
 |
 |
Using the altered structures for the reactants and products, the calculation was re-submitted. The codes for the optimisation to the boat transition state are shown below;
# opt=(qst2,noeigen) freq hf/3-21g geom=connectivity PartD_Boat_TS_ChangedAngles
The structure of the boat TS that was obtained from the failed QST2 calculation is shown below along with the correct boat TS structure obtained from manually altering the angles of the starting structures. The energy of the boat transition state was calculated to be -231.602802 Hartree and its point group was found to be C2v. The vibrations of the structure were analysed and one imaginary frequency was found with a value of -840.03 cm-1. This imaginary frequency was then visualised to ensure it followed the reaction coordinate expected. A representation of the motion of the imaginary frequency is shown below.
 |
 |
 |
As it has been possible to locate one imaginary frequency it can be confirmed that the transition state structure has been produced. The movement associated with this imaginary frequency is representative of that which occurs and bonds are broken and formed in the Cope Rearrangement. The energy of the boat transition state structure is considerably higher than that of the chair transition state. This implies that the Cope rearrangement will predominantly go via the chair transition state as reactions will always go via the transition state with the lowest energy. The boat conformation is higher in energy that the chair conformation due to the eclipsed nature of the carbon atoms within the structure. As a result the boat conformation suffers more steric strain than the chair conformation and so is less stable.
Part F
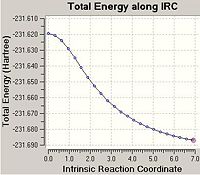
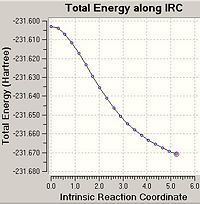
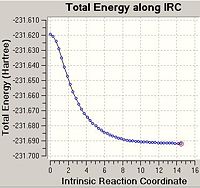
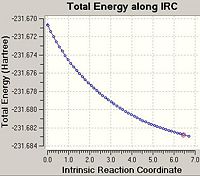
From looking at the optimised structures of the chair and the boat transition states in is almost impossible to predict which conformer of 1,5-hexadiene they connect. If I were to hazard a guess I would predict the the chair transition structure is connecting the gauche1 conformation and the boat transition structure is connecting the gauche3 transition structure. However, there is a function in Gausview called the Intrinsic Reaction Coordinate (IRC) method which follows the minimum energy pathway from the transition structure down to the local minimum of the potential energy surface. The method does this by taking small energy steps in changing the geometry of the structure in the direction where the gradient of the energy surface is the steepest.
Using the optimised transition structures obtained in the previous section, an IRC calculation was carried out on both the boat and chair structures. As the reaction coordinate is symmetrical for both the forward and backward directions of the Cope Rearrangement, it was chosen to only calculate the reaction coordinate in the forward direction. It was chosen to calculate the force constants for the reaction once, at the start of the reaction, and the number of points along the IRC to be calculated was set to 50. The codes for the IRC calculations are shown below:
# irc=(forward,maxpoints=50,calcfc) rhf/3-21g scrf=check guess=tcheck geom=(modredundant,connectivity,allcheck) genchk PartF_Chair_IRC
# irc=(forward,maxpoints=50,calcfc) rhf/3-21g geom=connectivity PartF_Boat_IRC
In the majority of cases this IRC method does not produce the minimal energy transition structure. Therefore, further calculations are necessary to ensure the global minimum energy structure is located. There are three possible further calculations that can be carried out: i) Take the last point on the IRC calculation and optimise the structure to a minimum (using the HF/3-21G method). ii) Restarting the IRC calculation and specifying a larger number of points until it reaches the minimum e.g. 150 points. iii) Re-calculate the IRC specifying the force constants to be calculated at every step.
As the first IRC calculation stopped after 23 points for the chair transition structure and 19 points for the boat it was therefore concluded that the second option 'redo the IRC calculation specifying 150 points' is a waste of time. It is clear that the IRC calculation does not need more points to calculate the minimum or it will have used the full 50 points allocated in the first calculation. Therefore, this option was not carried out. The first option is the fastest option, however, is the least accurate. The third option 'always calculate the force constants' takes the longest amount of time as it is the most computationally expensive however, it is the most accurate option. Therefore, option i) and iii) were both carried out on the end point of the original IRC calculation.
| Calculation Method | Chair | Boat | Discussion |
|---|---|---|---|
| IRC - Force Constants Only Calculated Once |   |
  |
The IRC calculation for the chair transition structure was complete after 23 steps and the calculation for the boat TS was complete after 19 points. It is clear that neither calculation has produced the minimal energy structure because, although the gradients of the graphs are decreasing, neither graph reaches a plateau. This indicates that in both cases the minimal energy structure has not been located and so further calculations need to be carried out on the final structures of the IRC calculations. The calculated energy for the chair transition structure was -231.6868 Hartree and for the boat transition structure was -231.6707 Hartree. Neither of these energies match that of the minimum energy given in Appendix1. |
| IRC - Force Constants Calculated at Every Step |   |
  |
Calculating the force constants at each point is a more computationally expensive method, however does give the most accurate results. From looking at the IRC graphs, in the case of the chair, the gradient reaches a plateau nicely which would indicate the minimal energy conformation has been located. In the case of the boat, the calculation completed before the IRC graph reached a plateau, which indicates the minimal energy structure may have not been located. The IRC calculation, when the force constants were calculated at every step, computed the energy of the chair transition state to be -231.619322 Hartree and the energy of the boat transition state to be -231.62310 Hartree. Therefore, the minimal energy structure, as predicted, has been located for the chair transition structure but not for the boat transition structure (when the energies are compared with those stated in Appendix1). |
| Minimisation of Last Point of IRC Calculation |  |
 |
The last point of the IRC calculation was taken and then submitted to a minimisation calculation. The method used was HF/3-21G. As the energy of the boat structure, stated above, was very close to that stated in appendix1, the last point of the IRC calculation, when the force constants were calculated at every step, was taken and then a minimisation was carried out on it. This yielded the structure shown in the table. The energy of this structure was calculated to be -231.69266 Hartree. A minimisation of the last point from the first IRC calculation was carried out on the chair transition structure which yielded the structure shown in the table. |
Part G
The activation energies for the Cope Rearrangement via both the boat and the chair transition states are to be calculated. Considering the reaction path, I decided to use the lowest energy conformation of 1,5-hexadiene, the gauche3/conformer5 structure, for the reactant. To do this, the boat and chair conformations were re-optimised using the DFT-B3LYP/6-31G(d) method and basis set and then a frequency calculation was carried out in order to locate the thermochemistry data for the two transition states. For the gauche3 conformer, the sum of electronic and zero point energies were calculated to be -234.468693 Hartree; this is used to calculate the activation energy of the reaction of 0K. The sum of electronic and thermal energies was calculated to be -234.461.464 Hartree; this is to be used to calculate the activation energy at 298K.
The thermochemistry data obtained from the reoptimisation of the chair and boat transition states using the DFT-B3LYP/6-31G(d) method and basis set and a subsequent frequency calculation are given below;
| Thermochemistry Term | Chair Energy / Hartree | Boat Energy / Hartree |
|---|---|---|
| Sum of electronic and zero point energies | -234.362213 | -234.402339 |
| Sum of electronic and thermal energies | -234.356026 | -234.396006 |
| Sum of electronic and thermal enthalpies | -234.355082 | -234.395062 |
| Sum of electronic and thermal free energies | -234.391445 | -234.43748 |
| Activation Energy | Chair / 0K | Chair / 298K | Boat / 0K | Boat / 298K |
|---|---|---|---|---|
| Hartree | -0.066354 | 0.052465 | -0.10648 | 0.065458 |
| kcal / mol | -41.63777253 | 32.92 | -66.8172231 | 41.07 |
| Reference / kcal/mol | 45.70 | 44.69 | 55.60 | 54.76 |
| Experimental / kcal/mol | 33.5 ± 0.5 | - | 44.7 ± 2.0 | - |
Therefore, as the activation energies for the Cope Rearrangement via the chair transtition state are lower compared to the boat transition state, it can be concluded that this is the preferred reaction path. This conclusion follows the initial predictions made through the rationalization that the chair structure is considerably lower in energy than the boat structure.
The Diels Alder Cycloaddition
The Diels Alder reaction is an organic reaction, or more specifically a cycloaddition, between a conjugated diene and an alkene which is also referred to as a dienophile. If the alkene is substituted, the Diels Alder reaction is a very useful way of forming substituted cyclohexene systems. The Diels Alder reaction is a pericyclic reaction which goes via a single transition state and it is this transition state that will be investigated in detail within this section of the report.
i) Cis-butadiene and ethylene (the starting materials in the above Diels Alder reaction) were modelled using Gausview, the structure was cleaned to ensure the starting structure was planar and then optimised using the AM1 semi-empirical molecular orbital method.
The code for the optimisation calculation of butadiene is;
# opt am1 geom=connectivity pop=full Butadiene_Opt
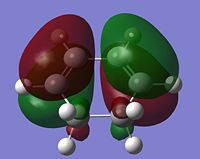
The optimised structure of butadiene and ethylene are shown below. The energy of the optimised structure of butadiene was calculated to be 0.04870719 Hartree and the point group was found to be C2v using the symmetrise function in Gausview. The molecular orbitals for butadiene and ethylene were also calculated. Representations of the HOMOs and LUMOs are shown below:
 |
| Butadiene | Ethene | ||||
|---|---|---|---|---|---|
| MO | Representation | Symmetry | MO | Representation | Symmetry |
| HOMO |  |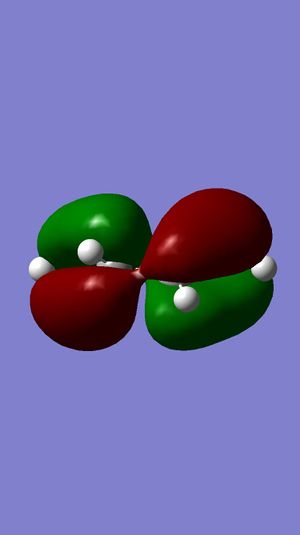
Antisymmetric | HOMO |  |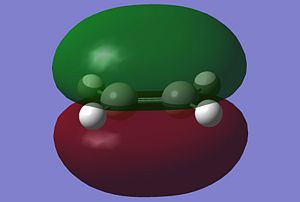
Symmetric |
| LUMO |  |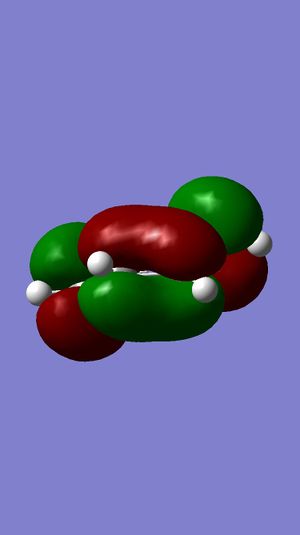
Symmetric | LUMO |  |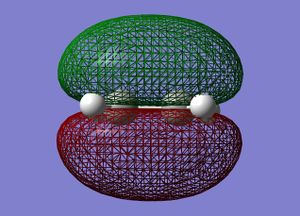
AntiSymmetric |
The symmetries of the molecular orbitals for butadiene and ethylene were deduced with respect to the σv plane. Molecular orbitals can only interact with each other if they have the same symmetry, therefore, the HOMO of butadiene can interact with the LUMO of ethylene and the LUMO of butadiene can interact with the HOMO of butadiene. There will be no interaction between the two HOMOs or the two LUMOs of these molecules are they are of opposite symmetry.
ii) The transition state for the above reaction is now to be investigated and the nature of the reaction path is to be analysed.
The transition structure for the above Diels Alder reaction is an envelope shaped structure as this maximises the overlap between the ethylene pi orbitals and the pi system of the butadiene pi system. The transition structure was modelled using Gausview and the length of the (dashed) forming bonds were chosen to be 2.2 Angstroms. This length was chosen as it is longer than a common C-C bond length which is approximately 1.5 Angstroms. The structure was submitted to an optimisation calculation to locate a transition state. The method used was the HF/3-21G method and the job-type was Opt+Freq, the optimisation was set to TS(Berny) and the additional key words were 'opt=noeigen'. The calculation, however, failed and it was presumed that the dashed bond lengths were set too long in the original starting structure. The dashed bond lengths were decreased to 2.0 angstroms and the job was re-submitted in the same way. In this instance the calculation was successful and the transition structure was located. The codes for the TS optimisation are given below;
# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity DielsAlder_TS_Opt
The optimised transition structure is shown below. To confirm that the transition state had in fact been located, the vibrations for the structure were checked. The structure shows one imaginary frequency which takes a value of -818.37 cm-1 and a representation of this imaginary frequency is shown below. The movement of the imaginary vibration is representative of what would be seen when the two (dashed) bonds are formed in the Diels Alder reaction.
 |
vibration.jpg) |
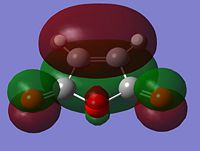
The Molecular orbitals of the transition structure were also calculated and a representation of the HOMO and the LUMO is shown below.
 |
 |
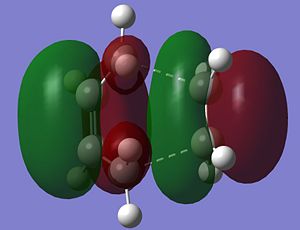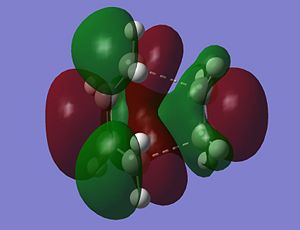The HOMO the transition structure of the Diels Alder reaction has antisymmetric symmetry. Therefore, this molecular orbital has been formed from the HOMO of butadiene and the LUMO of ethylene which are both also antisymmetric. In contrast, the LUMO of the transition structure has symmetric symmetry and so has been formed from the interaction between the LUMO of butadiene and the HOMO of ethylene which are both also have symmetric symmetry. The bond lengths of the starting materials can now be compared to those of the transition state, also the bond angles can be compared. Comparisons can also be made with the corresponding values stated in the literature [4].
| Starting Materials | Transition State Component | Literature Value | ||||
|---|---|---|---|---|---|---|
| Parameter | Butadiene | Ethylene | Butadiene | Ethylene | Butadiene | Ethylene |
| New/forming C-C sigma bond | 2.2 | 2.2 | 2.21 | 2.21 | - | - |
| C=C Double Bond | 1.335 | 1.326 | 1.37 | 1.376 | 1.349 | 1.329 |
| C-C Single Bond | 1.449 | - | 1.394 | - | 1.467 | - |
| C=C-C Angle | 125.7 | - | 121.4 | - | 124.4 | - |
| C=C-H Angle | 121.9 | 122.7 | 118.3 | 119.8 | 120.9 | 120.9 |
- New/forming C-C sigma bond: An good initial guess for the bond lengths of the new forming C-C bonds in the transition state was made as they have hardly changed during the optimisation calculation to locate the structure of the transition state. When comparing these bond lengths to a 'normal' C-C single bond e.g. the value stated for the C-C bond in butadiene (1.467 Angstroms), it is clear that these bond lengths are considerably longer. This is because the bonds are only partially formed and so are expected to be longer than a fully formed C-C sigma bond.
- C=C Double Bonds: In the case of butadiene and ethene the C=C double bond increases in length on forming the transition structure. This observation is what one would expect because during the Diels Alder reaction these bonds go from an initial double bond to a single bond in the final structure. In the transition structure these bonds are represented by a full bond and a dashed/partial bond. The literature values for these bond lengths correspond well to those calculated in the starting materials but again are considerably shorter than those calculated for the transition structure (for the same reasons as stated above).
- C-C Single Bond: In the case of both butadiene and ethylene the corresponding C-C single bond decreases in length on forming the transition structure. This result, again, is to be expected as the bonds are going from a single bond in the starting materials to double bonds in the final product structure. In the transition structure the bonds are represented by one full single bond and a partial/dashed bond. Again the literature values agree well with the calculated values in the starting materials.
- C=C-C Angle:The C=C-C angle in butadiene decreases in value on forming the transition structure. This is because the diels alder reaction forms a cyclohexadiene ring for the final product. The ring structure is a more strained structure and so has smaller C-C-C bonds compared to aliphatic structures. Again, the value for the C=C-C bond angle stated in the literature corresponds well with that calculated for the starting structure of butadiene.
- C=C-H Angle:As was the case for the C=C-C angle, the C=C-H angle also decreases on forming the transition structure; the half-way point between the aliphatic starting materials and the final cyclic product. The values stated in the literature correspond well with those calculated for the starting materials.
Part 3: The Regioselectivity of the Diels Alder Reaction
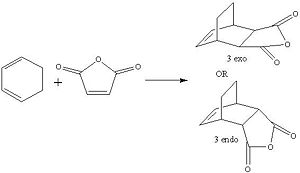
The reaction scheme shown opposite displays a facile reaction between cyclohexadiene and malaiic anhydride. The reaction is a stereoselective Diels Alder reaction in which the endo adduct is the major product. The reaction is kinetically controlled and therefore it is the energy of the transition states that need to be considered. As the exo adduct is the minor product, its corresponding transition state must be higher in energy than that of the endo product. That is to say that the activation energy associated with the formation of the exo product is larger than that associated with the formation of the endo product. In order to locate the two transition structures that correspond to the two products the starting materials for the reaction were modelled using Gausview. As an a good 'guess' can be made as to the geometries of the two transition structures, the starting materials can be arranged accordingly and then be submitted to the following calculation. The job type was set to opt+freq, the method and basis set were HF/3-21G, TS(Berny) was selected and the additional keywords were 'opt=noeigen'The following structures were obtained for the exo and the endo transition states.
# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity Malaiic_EXO_TS
Log File:DOI:10042/to-4262
# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity Malaiic_Endo_TS
Log File: DOI:10042/to-4263
 |
 |
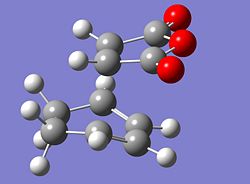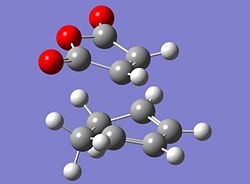To confirm that the structures obtained were in fact those of a transition state the vibrations were checked for each to ensure there was only one imaginary vibration. This was the case and the imaginary vibration for each transition state is represented below. The value for the imaginary vibrations are -806.17 cm-1 for the endo transition structure and -812.73 cm-1 for the exo transition structure.
 |
 |
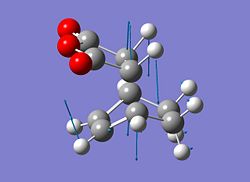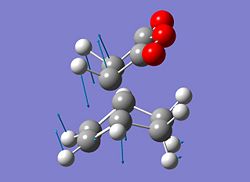The calculated energy for the endo transition structure is -0.05150 Hartree and the energy of the exo transition structure in -0.05039 Hartree. Therefore, the endo transition structure is the most stable of the two as it is lower in energy by 0.697 kcal/mol. The result is to be expected as the exo product displays the bridgehead of the cyclohexene ring on the same face of the molecule as the 3 oxygen atoms of the malaiic anhydride component. As a result there is a larger amount of steric clash experienced within this conformation which will destabilise it and therefore it is higher in energy. By contrast, the endo conformation has the bridgehead on the opposite side of the molecule to the malaiic anhydride component thereby minimising the steric clash between these two components.
| Nothing | Starting Materials | Transition States | ||
|---|---|---|---|---|
| Molecular Orbital | Cyclohexadiene | Malaiic Anhydride | Endo TS | Exo TS |
| HOMO | 
|
|
|
|
| Symmetry | Antisymmetric | Symmetric | Antisymmetric | Antisymmetric |
| LUMO | 
|
|
|
|
| Symmetry | Symmetric | Antisymmetric | Antisymmetric | Antisymmetric |
It is clear from the representations above that it is the HOMO of cyclohexadiene and the LUMO of malaiic anhydride that interact with each other to form both the endo and the exo transition states. This is an allowed interaction as it involves molecular orbitals of the same symmetry. Aside from steric reasoning, the endo transition structure is more stable than the exo transition structure due to the presence of secondary orbital overlap. Primary orbital overlap interactions are the overlaps between molecular orbitals that form bonds. Secondary orbital overlaps, although do not result in bond formation, are bonding and stabilising overlaps, in this case, between the pi orbital of the C=O groups on the malaiic anhydride component of the endo transition structure and the pi orbitals on the dienophile (the cyclohexadiene)[5]. Secondary orbital overlaps are not possible on the exo structure due to the malaiic anhydride component being orientated away from the diene. The diagram below shows the primary orbital overlap which leads to the formation of the new C-C sigma bond and the stabilising secondary orbital overlap. Additionally, the secondary orbital overlap can be viewed in the representation of the HOMO-1 MO of the endo transition structure.
 |
 |
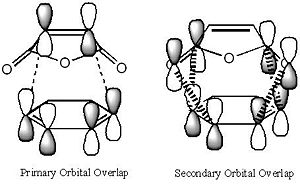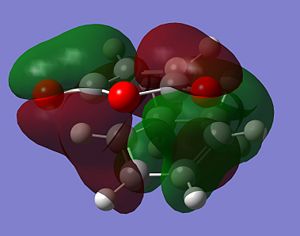| Parameter | Endo / Angstroms | Exo / Angstroms |
|---|---|---|
| Length of new/forming C-C sigma bonds | 2.162 | 2.169 |
| Distance between C=O group and opposite CH2CH2 group | 2.330 | 2.329 |
| Distance between the anhydride C=C and the diene C=C | 2.700 | 2.637 |
| Distance between the two C=O groups | 2.279 | 2.279 |
References
- http://pubs.acs.org/doi/pdf/10.1021/jp8109385
- http://openlearn.open.ac.uk/file.php/2937/T838_1_025i.jpg
- http://www.journalarchive.jst.go.jp/jnlpdf.php?cdjournal=bcsj1926&cdvol=50&noissue=8&startpage=2119&lang=en&from=jnlabstract
- http://www.hbcpnetbase.com/
- http://pubs.acs.org/doi/pdf/10.1021/jo9620223?cookieSet=1
