Rep:Mod3:kr207fin

The Transition State

This module can be seen as an extension of module 1. IThe molecular mechanics/force field method used in module 1 is limited to structural determination of global minima. It cannot describe bonds being made and broken and changes in electrondistribution. However, in order to get a better insight into the reactivity of a reaction, the transition states and subsequently the breaking and forming of bonds has to be studied. Therefore, in this module molecular-orbital methods were used instead to locate transition structures on the potential energy surface shape. Gaussian calculations were run to solve the Schroedinger equation. In the following the reactivity of 2 reactions: The Cope rearrangement of 1,5-hexadiene and the Diels-Alder Cycloaddition of Ethylene and Cis-Butediene were investigated. The transition states were optimised, and using the data computed, the reaction pathways and reaction barriers were determined.

The Cope Rearrangement Tutorial

In this tutorial the chemical reactivity of the Cope rearrangement of 1,5-hexadiene was investigated using Gaussian.

Cope rearrangement of 1,5-hexadiene

This is an example of a [3,3]sigmatropic cope rearrangement. An allyl group migrates suprafacially across the conjugated system, which involves a total electron count of 6. This corresponds to 4n+2. Hence, under thermal conditions this reaction proceeds via a hueckel topology transition state. This concerted pericyclic reaction can proceed via a transition state in "chair" or "boat" conformation.

2 possible Transition State structures

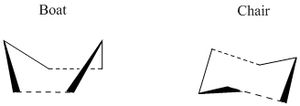
Using Gaussian and different levels of theory the preferred transition state structure was found and the actvation energies were calculated to determine the preferred reaction mechanism.

Optimising the Reactants and Products

Before the transition state of this reaction can be further investigated, the optimised product (and reactant) structure had to be determined. This 1,5-hexadien can exist in "gauche" or "anti" conformation. Gauche and anti refer to the linkage of the four central C-atoms.

2 possible conformations of the 1,5-hexadiene

These 2 possible structures were optimised using the low-level, but sufficient HF/3-21G basis set. They were first drawin gaussview and then cleaned before running the calculation.

Based on an steric argument it was expected that the anti-conformation is more stable due to reduced steric repulsion with the 4 central C-atoms at an dihedral angle of 180° as oppose to the sterically more demanding eclipsed conformation of the central Cs (dihedral angle = 0°) in the gauche conformation.

The following table 1 shows a summary of the 2 final structures obtained.

Table 1: Summary of the 2 final gauche and anti structures of 1,5-hexadiene optimised

Conformer	Energy / a.u.	Point Group	Structure
anti2	-231.69254	Ci	Taxol 11
gauche3	-231.69266	C1	Taxol 11

The gauche conformer was optimised to a total minimum energy of -231.69266120a.u. and the anti conformer was found to have a total energy of -231.69253528a.u., which corresponds to a relative energy difference of 0.3308 kJ/mol or 0.079kcal/mol. Contrary to what was initially expected, based on these energies the gauche product was found to be lower in energy by 0.3308 kJ/mol and thus is more stable. This is assumed to be due to the CH-π interaction . A weak stabilising H-bond is formed from overlap between the π-orbital of the C=C double bond and the nearby δ* orbital of the vinyl proton (soft acid-base interaction). This favourable stabilising π_C=C - σ*_C-H overlap becomes more evident from the Newman projection of the gauche and anti-conformer.

Newman projection of anti2 and gauche3

In fact, the energy difference of 0.3308 kJ/mol found above is very small and based on the CH-π interaction should be more significant, however, one of the limitations of the Hartree-Fock method used in this experiment is that it does not consider these forms of electron-correlations accurately, only giving rise to a small energy difference.

From these Newman projections it can also be seen that the anti2-conformer has an inversion of symmetry, which is not present in the gauche3 structure. Initially, for the anti conformer 2 point groups were found. Therefore, the calculation was repeated and to ensure that the symmetry of anti2 is C_i whenn running the calculation for this anti-conformer its symmetry was constrained to the point group C_i with very tight tolerance (0.0001). The symmetry point group was determined by using the "symmetrize" optiion under the edit menu.

1,5-hexadiene has readily rotating C-C single bonds, therefore many different variations of each conformer can be found. Upon comparing the structures obtained, their energies and point groups with those in Appendix 1, the 2 structures computed were identified as anti2 and gauche3. The data obtained is in agreement with the data shown in appendix 1.

Further optimisation of the anti2 conformer
The anti2 conformer was then optimised again using the higher level basis set, B3LYP 6-31G*. This was achieved using the following settings: Method DFT, B3LYP, 6-31G and (d). The following table shows a summary of the data computed using the low level theory HF/3-21G and the high level theory B3LYP/6-31G*.

Table 2: Comparison of geometric data obtained for anti2 using 2 different basis sets

Basis set used	Bond length	Torsional angle	Torsional angle / °
			C2-C3-C4-C5	C1-C2-C3-C4	C6-C5-C4-C3
HF 3-21G			180.0	114.7	114.7
B3LYP 6-31G*			180.0	118.8	118.8

As expected it was found that using a larger, higher level basis set gives a better fit of the real ground state of that specific compound. A lower, i.e. more stable minimum of the anti2 structure was obained, indicating a better fit of the ideal equilibrium structure. It was found that the calculation took longer using the higher level of theory.

As for structural changes: the bond length in ant2 remain constant. There is an insignificant change, which, however, is smaller than the inherent error of bond lengths computed using Gaussian, namely +/- 0.01Å. Another indication that a higher level of theory gives a better approximation of the real minimum structure is that in the structure obtained using the larger 6-31G* basis set, the C=C and C-C bond lengths are in better agreement with literature values: C=C lit. double bond length = 1.34Å and C-C lit. single bond length = 1.54Å. The C-C single bond adjacent to the double bond is slightly shorter due possible delocalisation of the double bond.

The main difference is that the outer dihedral angles change by 4°. Furthermore, the symmetry of the outer dihedral angles and the symmetry in terms of bond lengths underlines the C_i symmetry of the anti2 conformer.

Vibrational analysis of the anti2 conformer using both levels of theory
In addition to the optimisation a frequency calculation for anti2 was carried out (i.e. using the same basis set 6-31G*) to confirm that the minimum structure of anti2 was indeed optimised.

IR spectrum of anti2 conformer of 1,5-hexadiene

All vibrational frequencies were positive and real, which confirmed that the structure optimised in the previous step is at its minimum, i.e. in its ground state. The frequency analysis is the second derivative of the potential energy surface. If the curvature, i.e. the second derivative is +ve, the minimum of the curve was found. Therefore, the +ve vibrational frequencies obtained confirm that anti2 is in its ground state. A -ve frequency would indicate a maximum, which would mean that anti2 is in a higher transition energy state and not at the lowest possible point of the PES-curve. Anti2 is in its equilibrium point where nuclei-nuclei repulsion and attractive nuclei-electron interactions balance each other out and the lowest possible potential energy is reached. At this equlibrium bond distance at which Nuclear-nuclear repulsion, nuclear-electron attraction and electron-electron interactions are most stabilised.

Furthermore, from the .log-output it can be seen that the job, i.e. all net forces and displacements have been fully converged. This optimisation was successful since the RMS gradient, the RootMeanSquare, essentially indicating the deviation of the total energy from the ideal minimum, is close to 0 and <0.001 a.u.

Table 3: Summary of thermochemical data of anti2 conformer obtained from vibrational analysis

Thermochemistry	Energy / a.u.
Sum of electronic and zero-point Energies ... E = Eelec + ZPE	-234.469216
Sum of electronic and thermal Energies ... E = E + Evib + Erot + Etrans	-234.461865
Sum of electronic and thermal Enthalpies ... H = E + RT	-234.460920
Sum of electronic and thermal Free Energies ... G = H - TS	-234.500806

Note, that in order to obtain "thermochemistry" data for the anti2 structure optimised using the lower level, a frequency analysis using the HF 3-21G level was also carried out, the data was the used to calculate activation energies and the enthalpy (see at the end of this exercise).

Optimising the "Chair" and "Boat" Transition Structures

The aim of this part was to optimise transition structures using different methods: optimisation by computing the force constant at the beginning of the reaction, by using the Frozen Coordinate method via the redundant coordinate editor and by using QST2. After that the reaction coordinate was also visualized, an IRC was run and the activation energies for the cope rearrangement via the chair and the boat transition structures were calculated.

Chair transition structure

The chair transition structure was optimised using 2 different approaches: Optimisation to a TS(Berny) by computing the force constant once and Frozen Coordinate method by using the redundant coordinate editor. The following table 4 shows the final output of these calculations.

Table 4: Comparison of the 2 chair transition structures obtained from both methods

	Optimisation to a TS(Berny)	Frozen Coordinate Method
Transition Structure	Optimised chair transition state	Optimised chair transition state
Terminal C-C distance /Å	2.02	2.02
Imaginary frequency / cm-1	-818.03	-817.92
Corresponding vibration mode

Optimisation to a TS(Berny) by Force constant calculation
For the Force constant calculation, the 2 allyl fragments were first optimised using the HF 3-21G level of theory. These optimised fragments were then pasted twice into a new gaussview window and were subsequently manually placed in the approximate transition structure. The 2 terminal ends of the 2 allyl fragments were placed within a distance of 2.2Å of each other.

This method is highly sensitive to the input structure. If the guessed structure is not good enough this optimisation will not give the correct transition structure. However, since the transition structure was well known, this method gave a good fit of the transition structure - as shown in the table above. If you have reasonable guess for the transition structure geometry, this method is relatively easy and works well. For this method the force constant matrix, the Hessian is computed in the first optimisation step and subsequently constantly updated as the optimisation proceeds. This method fails, if th einput structure is far away from the ideal because the curvature of the PES curve for this poor input structure may significantly deviate from the actual transition structure PES and hence the wrong transition structure geometry would be optimised.

In addition, a frequency analysis was carried out to confirm the successful optimisation. An imarginary frequency at -818.03cm^-1 was found. This vibrational mode corresponds to the Cope-rearrangement, i.e. vibration along the bond formed and broken during this rearrangement. When running the calculation in gaussian the additional keywords: Opt=NoEigen were added to ensure that no more that one imaginary frequency are found in case the input guessed structure is not good enough. Contrary to optimisation of a ground state, when optimising to a transition state, a -ve frequency is desired, since the transition state is a maximum in energy along the Potential energy surface of a compound. This will be further explained in the Diels-Alder section.

Frozen Coordinate Method
For this method 2 steps are needed. Similarly to above the optimised allyl fragments are place in a transition structure-like arrangement. Then, in the first step the distance between the 2 termini of the 2 allyl fragments is set to a fixed value of 2.2Å. The structure was then optimised with the constraint that this distance remains at 2.2Å. This reaction coordinate is frozen, and the rest fo the molecule is then optimised. In the second step the distance between the 2 termini in that pre-optimised structure was then relaxed. Again, a freqeuncy analysis was carried out.

An advantage of this method compared to the force constant calculation is that in the frozen coordinate approach not the whole hessian has to be computed. It is only differentiated along the reaction coordinate.

As can be seen from the table above the final optimised transition structures using these 2 methods are in high agreement and are nearly identical with the terminal end of the allyl fragment 2.02Å separated. Both methods are therefore equally accurate in this case. The Frozen Coordinate Method is less expensive and more time-efficient since - as mentioned above - it is only differentiated along the reaction coordinate, which was found to give a sufficiently good guess of the initial force constant matrix. However, a reasonable guess of the terminal distance between the 2 fragments has to be known. For the Force constant method the guessed structure has to be reasonably accurate, as otherwise the optimisation will fail.

Furthermore, both animated vibrational frequencies show one C-C bond forming, whilst the other opposite one is breaking, this indicates asynchronous bon formation in this pericyclic reaction.

Boat Transition Structure

In order to optimise the Boat transition structure a different method was used. For this optimisation the QST2 method was used. For this method the reactant and the product have to be specified and the transition state in between them will be calculated as intrapolation between these starting and final structures. The following image shows the input of the reactant and product structure before the calculation was run. The numbering was changed manually to match the reaction.

Numbering of the Reactant-like input-structure

Numbering fo the Product-like input-structure

Note that these images already correspond to the revised structure input to ensure successful optimisation.

Initially, the calculation was run with the anti2 reactant and product unchanged in sructure (i.e. as seen in the first part). However, this calculation failed to give the right transition state geometry.

Failed computation of the boat transition state

This is due to the readily rotation of the central C-C single bonds. The input structures were too unreasonable. A shortcoming of the QST2 method is that the product and reactant structure have to be drawn so that they can be closely related to the transition state, otherwise the method cannot interpolate between them.

To avoid this the geometry of the reactant and product were changed to resemble the expected transition state structure (how can be seen in the image at the top), before a second calcultion was run. The central C-C-C-C dihedral angle was changed to 0° and the 2 central C-C-C bond angles were changed to 100°.

This gave the optimised boat transition structure. Successful transition state optimisation was confirmed by the vibrational analysis. One imaginary frequency was found at -839.94cm^-1, which corresponds to the bonds formed in the process of the cope rearrangement.

Imaginary frequency vibration of the boat transition state

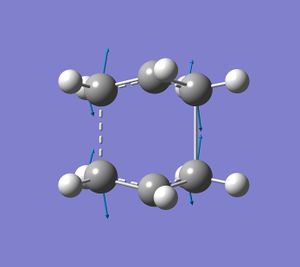
Again, 1 bond forming vibration and 1 bond breaking vibration was found, indicating asynchronous bond formation in this reaction pathway.

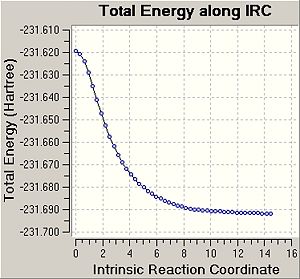
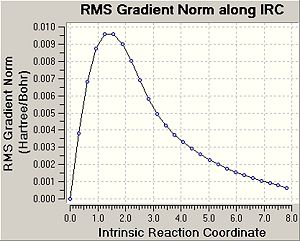
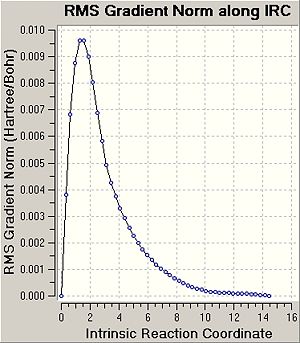
Intrinsic Reaction Coordinate

It was tried to predict the conformers of 1,5-hexadiene that will be formed based on the transition structures obtained above. Therefore, in this part the minimum energy path from a transition structure to its local minimum on the potential energy surface was studied to get a better idea about the conformers of 1,5-hexadiene. The following table shows a summary of the this IRC method.

Table 5: Summary of IRC calculations for the chair transition state

	Calculate Force Constants Once	Calculate Force Constants always
Points along IRC	26	47
IRC energy pathway
IRC RMS gradient
Final structure of IRC
Energy / a.u.	-231.68907549	-231.69166432

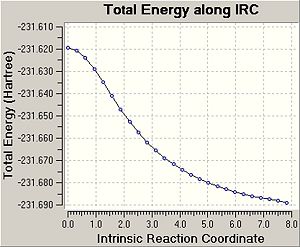
In this case the reaction coordinate is symmetrical and was therefore only computed in the forward direction. Initially, the force constant was only calculated for the first stepDOI:10042/to-3549 . The number of points along the IRC was set to 50. For the first IRC calculation the force constant was calculated once, however it was found that the calculation hasn't reached a minimum yet. Therefore, it was decided to repeat the IRC calculation with the difference that force constant is now calculated at every step (always)DOI:10042/to-3547 . This is more expensive, however it is the most reliable method. Using these settings, a minimum structure was able to be computed. Another option could be to take the final point of the IRC and run a normal optimisation or to restart the IRC and specify a larger number of points. Since the first calculation only needed 26 steps, when specifying 50 points, this would have not improved the calculation. Therefore, when restarting the IRC the force constant was decided to e calculated at every step. It can be seen that now 47 points are calculated when the IRC RMS gradient reaches 0, i.e. the optimum minimum has been found. In the previous method with calculate force contant once, the IRC gradient did not reach 0, indicating incomplete optimisation Furthermore, the energy of the final structure is not levelling off, indicating that the minimum has not been optimised yet.

It can be seen that geometry of the conformer is optimised and the energy calculated gives the PES curve of this reaction. Therefore, the aim of this process is to reach the point where the gradien or the slope of the energy surface is steepest since the optimimum transition structure has to be found. Upon calculating the force constant always the reaction coordinate is steepest. The RMS essentially describes the deviation of the calculated structure from the ideal, and hence the final structure is assumed to be found in the second IRC calculation.

The energy of the final IRC optimised structure is idential with the gauche2 energy as shown in Appendix 1 in the module 3 instructures. This indicates that the reaction gives the gauche2 conformer of 1,5-hexadiene and proceeds through a chair transition state. To confirm this the activation energies were calculated in the following section.

Calculation of Activation Energies

The transition structures previously optimised were further optimised to a higher level of theory, namely B3LYP/6-31G*. The following table shows the results and the data used to calculate the activation energies shown in table7.

Table 6: Thermochemistry Data of the chair and boat transition structures

	HF/3-21G			B3LYP/6-31G*
	Electronic energy / a.u.	Sum of Electronic and zero point energies at 0K / a.u.	Sum of Electronic and thermal enthalpies at 298.15K / a.u.	Electronic energy / a.u.	Sum of Electronic and zero point energies at 0K / a.u.	Sum of Electronic and thermal energies at 298.15K / a.u.
Chair Transition State	-231.619322	-231.466700	-231.461340	-234.556984	-234.414931	-234.409010
Boat Transition State	-231.602802	-231.450929	-231.445300	-234.543093	-234.402342	-234.396008
Reactant anti2	-231.692535	-231.539539	-231.532565	-234.61170997	-234.469216	-234.461865

Table 7: Summary of acitvation energies

	HF/3-21G		B3LYP/6-31G*		Experimental Data
	at 0K	at 298.15K	at 0K	at 298.15K	(0K)
ΔE Chair	45.71	44.69	34.06	33.17	33.5 +/- 0.05
ΔE Boat	55.60	54.76	41.96	41.33	44.7 +/- 2.0

For both levels of theory the values computed agree with Appendix 2 in the module 3 instructions. Also, as a higher level of theory is used the energy is lower and also the activation energies are in better agreement with experimental values , indicating the better accuracy of the higher B3LYP 6-31G* level of theory. However, the low level method is still sufficient to give the right trend. For all values calculated ΔE of the chair is smaller than ΔE of the boat transition structure. This means that the activation energy needed to go to the chair transition state is lower than for the reaction leading to the boat transition conformer. Its lower energy also indicates that the chair transition state is more stable. Therefore, it is assumed that this coperearrangement proceeds via the lower energy, more stable chair transition state.

Therefore, overall the cope rearrangement reaction is assumed to proceed from the reactant anti2 through the chair transition structure to the gauche2 conformer.

DOIs for higher level TS structure calculations: chair DOI:10042/to-3551 , boat DOI:10042/to-3552

References

Background reading:

1. Density Functional Theory Isotope Effects and Activation Energies for the Cope and Claisen Rearrangements: Olaf Wiest, Kersey A. Black, K. N. Houk, J.Am.Chem.Soc., 1994, 116(22), 10336-10337 DOI:10.1021/ja00101a078
2. An analysis of the conformers of 1,5-hexadiene: Brandon G. Rocque, Jason M. Gonzales , Molecular Physics, 2002, 100 (4), 441-446 DOI:10.1080/00268970110081412

The Diels Alder Cycloaddition

In this part the Diels Alder Cycloaddition and its reactivity was investigated using Gaussian transition state calculations. Further information on the bond forming and breaking process in the diels-alder reaction was obatined from analysis of molecular orbitals and vibrational frequencies computed. The Diels-Alder reaction is a pericyclic reaction and proceeds via a concerted mechanism, during which 2 or more σ-bonds are formed between the termini of 2 or more conjugated π-systems. In this exercise the HOMO-LUMO interaction of 2 reactants to form 2 new bonding-antibonding MOs was examined. It was then looked at the effect of substituents on the π-orbitals in terms of stabilising the regiochemistry of the main outcome of a DA reaction.

All calculations carried out were based on the AM1 semi-empirical molecular orbital method.

Ethylene and Cis-Butadiene

Diels-Alder reaction between cis-butadiene and ethylene

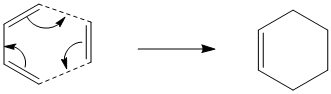
As can be seen this Diels Alder addition proceeds via a [4_πs-2_πs] concerted mechanism since there are 4π orbitals in the π system of butadiene and 2π orbitals on ethylene. This corresponds to a total electron of 6, which fits 4n+2 and hence, under thermal conditions, indicates a Hueckel topology transition sate with suprafacial components only.

To get a better idea of whether this reaction proceeds in a concerted stereospecific fashion, i.e. allowed, or not, i.e. forbidden, the MOs of the 2 reactants and the resulting transition state were computed.

Optimisation and Analysis of the reactants Ethylene and Cis-Butadiene

To begin with, butadiene and ethylene were optimised based on the AM1 semi-empirical method. This gave energies of 0.04879748Hartrees for cis-butadiene and 0.02619024Hartrees for ethylene, which corresponds to 30.620888kcal/mol and 16.434627kcal/mol, respectively.

Optimised Cis-Butadiene

Optimised Ethylene

A summary of the HOMO and LUMO of both reactants is shown in the table below. The symmetry of the MOs was determined with respect to the plane of symmetry as shown in the instructions for this module.

Table 8: FMOs of reactants

Reactant	Molecular Orbital	Visualisation		Energy / a.u.	Symmetry wrt the plane
Cis-Butadiene	LUMO			0.01712	Symmetric
	HOMO			-0.34386	Anti-symmetric
Ethylene	LUMO			0.05284	Anti-symmetric
	HOMO			-0.38777	Symmetric

The more nodes, i.e. ou-of-phase overlap in the MO, the higher the energy of the MO. Therefore the π-orbital of ethylene is lowest in energy and the π*-orbital of ethylene is least stable since it has anti-bonding interactions only. In constrast to this, the HOMO on cis-butadiene has more bonding that anti-bonding out-of-phase interactions and is therefore relatively stable. Also, the LUMO on cis-butadiene is close to non-bonding (i.e. close to 0a.u.) since anti-bonding and bonding interactions are close to cancelling each other out.

Optimisation and Analysis of the Transition State

Geometry of the guessed transition structure input

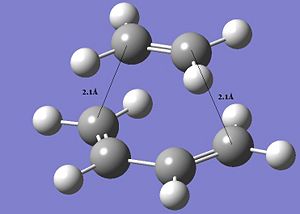
The transition state structure of this reaction was then computed and based on the AM1 semi-empirical orbital method. It was decided to use the force constant calculation. The settings for the calculation included: Opt+Freq, Optimisation to a TS(Berny), Calculate Force constant always, and in the additional keyword box: Opt=NoEigen to limit the calculation to one imaginary frequency. It was decided on this method, since we already roughly know what the transition state is expected to look like, namely with the ethylene approaching from above the plane. And the distance between the 2 termini of the conjugated systems was assumed to correspond to ≈2.1Å. If the guessed transition structure is good enough, this method is sufficient. The Frozen Coordinate method would be another option, however in this case the terminal distance is set to a fixed length, which limits the structural optimisation of the rest of the compound. Using this frozen coordinate method, it was found that a transition state with a very distorted cis-butadiene conformation was computed.





Vibrational Frequency Analysis
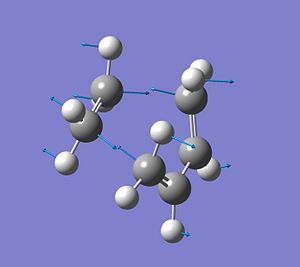
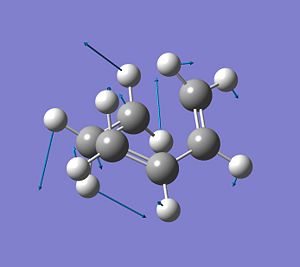
Vibrational analysis confirmed that the optimisation was successful. It was found that for this transition state there is one imaginary frequency at -955.47cm^-1, which corresponds to the vibration of the 2σ-bonds that are being formed during this reaction process. This indicates that a transition state has been optimised. From the displacement vecotors it can be seen that the imaginary frequency describes the synchronous formation of 2 bonds, i.e. the bond formation occurs at the same time. Furthermore, the next lowest possible frequency is at 147.47cm^-1 and corresponds to the rocking motion of the ethylene-Hs. There is no bond forming or bond breaking connected to this vibration. It shows that ethylene is not involved in the reaction pathway. It is simply a low energy vibration that therefore could take place at RT, since kbT is enough energy input to cause this vibration.

Imaginary vibration at -955.47cm-1

Low frequency vibration at 147.47cm-1

Essentially, the frequency calculation is the second derivate of the potential energy surface, i.e. it describes the curvature of the potential energy vs r (bond distance). If a -ve frequency is found, this shows that we are a maximum of this PES curve, i.e. a high energy transition state has been optimised.

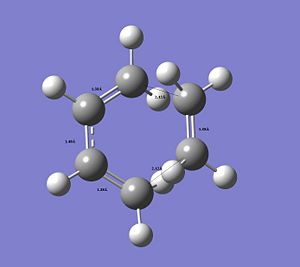
By measuring the CC bond distances in the transition state, further insight into the reaction mechanism can be obtained, as well as confirmation that the correct transtion state structure was optimised (please click on image to view bond distances).

C-C bond distances in the transition state

2D sketch of forming and breaking bonds

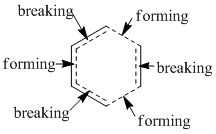The typical sp³Carbon C-C single bond length is 1.54Å and the typical sp² Carbon C=C double bond length is 1.34Å. The fact that in this image as seen the C=C are longer compared to literature and the C-C single bonds as seen are shorter and in between the typical single and double bond distance confirms that a conjugated transition state was optimised with delocalised double bonds in transition from a double bond to a single bond or vice versa (see simple 2D image) with delocalised electron-density. The C=C double bonds as seen are in better agreement. The distance between the termini of the 2 conjugated systems is longer that a typical C-C single bond. However, the VdW radius of a C-atom is 1.71Å. This confirms the ongoing formation of the 2 new σ bonds forming between the ethylene and the cis-butadiene. The distance between the 2 termini between the reactants is shorter than 2 x the typical VdW radius of Carbon, which indicates that a bond is formed. The 2 termini Carbond atoms are close enough to each other to form a bond and share electron density. Since this is the transition state the bond has not actually been formed yet.
Also, as can be seen the bond distances in this transition structure are symmetrical. The 2 new, terminal distances are identical. This also indicates synchronous formation of the 2 new sigma bonds in the concerted reaction process. This synchronous bond formation of the 2 new sigma bonds in this DA cycloaddition was already confirmed by the vibrational analysis and the fact that only one imaginary frequency was obtained.
Molecular Orbital Analysis
In order to investigate the HOMO-LUMO interaction between the 2 reactants the HOMO and the LUMO of the transition structure were tabulated below.

Table 9: FMOs of Transition State

Molecular Orbital	Visualisation	Energy / a.u.	Symmetry wrt the plane
LUMO		0.02314	Symmetric
HOMO		-0.32394	Anti-symmetric

https://www.ch.imperial.ac.uk/wiki/images/0/06/TSDASIMPLEREPONEO_OPTFREQ.LOG

Comparing these MOs of the transition state to the reactant MOs it can be seen that the HOMO of the transition state if formed from the overlap of the HOMO of cis-butadiene and the LUMO of ethylene. This HOMO of the transition structure describes the bonding orbitals of the 2 new single bonds formed. This is consistent with the conservation of orbital symmetry in Diels-Alder cycloaddition. This describes the fact that the symmetry of the new orbital formed must be the same as the symmetry of the overlap of the orbitals it is derived from. In order to have significant overlap and thus form bonding MOs, the substituent orbitals must have sufficient electron density overlap, i.e. stabilising in-phase overlap. For this to be the case the reactant MOs must have the same symmetry. The LUMO of ethylene and the HOMO of butadiene are both anti-symmetric. This HOMO-LUMO pair interacts and give the anti-symmetric HOMO of the resulting transition state adduct, with 2 new sigma bonds.

Similarly, the LUMO is symmetric and formed from overlap of the substituent reactant MOs, namely overlap of the s HOMO from ethylene and the s LUMO from butadiene. This transition adduct LUMO describes the anti-bonding out-of-phase overlap along the 2 new bonds formed.

Both these HOMO-LUMO interactions have significant electron density overlap since they are of the same symmetry and therefore the reaction is symmetry-allowed. This also shows that orbital symmetry control determines the pathway of this reaction, at which the symmetry of the reactant and product MOs remain the same.REFFFF Conservation of orbital symmetry.

In addition, apart from the symmetry argument, the relative energies of the cis-butadiene HOMO-LUMO and the π-π* orbital of ethylene can be used to determine the HOMO of the transition structure. In order to achieve the best overlap and hence greatest stabilisation, both the symmetry has to match to have in-phase overlap, but also the relative energies of the substituent MOs. As can be seen from Table 8 the LUMO of the ethylene and the HOMO of the butadiene are closest in energy. Their energy difference is 248.933kcal/mol (vs 254.072 of the vice versa overlap), giving rise to the greatest stabilisation of the resulting bonding HOMO orbital in the transition state. This corresponds to the normal electron demand with the dienophile providing the LUMO and the diene providing the HOMO.

Cyclohexa- 1,3-diene and Maleic Anhydride

Diels-Alder reaction between Cyclohexa- 1,3-diene and Maleic Anhydride

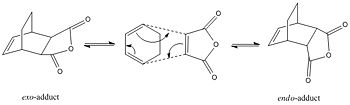
In this part the regioselectivity of the Diels-Alder reaction was examined and the effect of subsituents on the major outcome of the reaction was subseqeuently determined. This reaction is also a [4_πs+2_πs] concerted pericyclic cycloaddition. There is 6 conjugates π electrons in this reaction, which fits 4n+2. Subseqeuntly, under thermal conditions this reaction must proceed via a transition state in the Hueckel topology and all components mus react supraficially. Nevertheless, as seen in the sketch above this reaction can afford 2 diastereoisomers as product, the endo- and the exo-adduct. The primary product of the cycloaddition of cyclohexa-1,3-diene and maleic anhydride give the endo-adduct as primary product. Furthermore, as already discussed in module 1 this Diels-Alder cycloaddtion is assumed to be kinetically controlled, with the exo-transition state being higher in energy. In the following the transition states leading to both products were computed to examine this further and were then analysed using molecular orbitals computed.

Optimisation of the Transition Structures

The transition structure was optimised using the Force constant calculations. As previously, the calculations were based on the AM1 semi-empirical molecular orbital method. The following settings were selected: opt+Freq, Optimisation to a TS(Berny), and the force constant was calculated at every step (i.e. always), using the additional keywords:Opt=NoEigen in case the guessed structure is not good enough. Even though this method is the most expensive, it gives the most reliable result and the compound is not too large to use this method. An approximate transition structure was drawn in Gaussview: this input structure was then optimised manually first by changing the bond lengths, bond types and the dihedral angles. The structure was changed to be most symmetrical. It was cleaned and symmetrized several times, until a good guess of the particular transition structure was obtained. The distance between the 2 terminal C that form the 2 new σ bonds was estimated as 2.2Å. Particular attention was also paid to the positioning of the Hs, as shown in the Table below.

Table 10: Summary of exo- and endo-transition structures

	Exo TS	Endo TS
Input-orientation of Hs
Energy / a.u.	-0.05041985	-0.05150480
Energy / kcal/mol	-31.638940	-32.319757
Final structure	Taxol 11	Taxol 11

endo-TS DOI https://www.ch.imperial.ac.uk/wiki/images/c/c7/TSHUP_OPTFREQ.LOG exo-TS DOI https://www.ch.imperial.ac.uk/wiki/images/0/09/EXOTSDA_OPTFREQ.LOG

Analysis of the Transition Structures

The data obtained was then analysed to determine the regiochemistry of this reaction and relative stabilisation of the transition states.

Relative Energies of both transition states
Based on steric arguments the exo-product of this reaction is assumed to be the thermodynamic product, i.e. the most stabilised product due to reduced steric hindrance between the bridge and the maleic anhydride, since the Hs on maleic anhydride are pointing down in the exo conformation and thus steric clash is reduced. This steric clash in the endo-conformation is also referred to as 1,3-Diaxial Compression between the pointing up Hs on the ring-linkage and the Carbon bridge. This destabilising compression is reduced in the exo-conformation with the Hs on the other face of the ring.

Nevertheless, as mentioned at the outset the main outcome of this reaction is the endo-product, i.e. the higher energy kinetic product. Therefore, this reaction is assumed to be under kinetic control. In short, rather than the total energy, i.e. the stability of the product, the energy and hence stabilisation of the transition state controls the outcome of the reaction. The rate of the reaction, i.e. the activation energy barrier leading to the transition state determines the major product of this reaction.

From the optimisation calculations carried out above, the endo-transition structure was found to be more stable by 0.681kcal/mol. Therefore, the activation barrier is lower to get to the endo-transition state. Hence, the reaction pathway leading to the endo-transition structure and subsequently the endo-adduct, proceeds at a faster rate and the endo-adduct will be the major adduct under kinetic control and irreversible reaction conditions. The exo-transition structure leads to the exo-product formed under thermodynamic control.However, it has to be taken into account that this energy difference is not very significant since the inherent error of gaussian energy calculations is ≈5kJ/mol, which corresponds to 1.2 kcal/mol. This indicates one of the limitations of these Diels-Alder reactions.

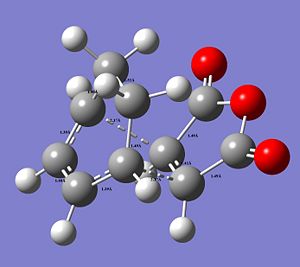
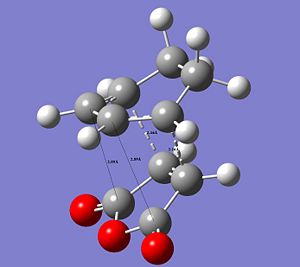
The following images show the CC distances in both transtition structures.

C-C bond distances in the endo-TS

C-C bond distances in the exo-TS

internal C-C bond distances in the endo-TS

internal C-C bond distances in the exo-TS

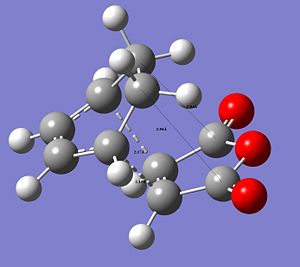The CCbond lengths are very similar in both structures as well as the length of the newly forming CC σ-bonds with 2.17 and 2.16Å. Similarly to the analysis of the bond lengths for the butadiene-ethylene transition state, here the developing and breaking double bonds have a similar length, in between the typical single and double bond length. The 2 terminal C in between the 2 new bonds are formed are close enough, i.e. < 2xtypical VdW radius of C-atoms, to allow bond formation. Particular attention can be paid to the through space interaction between the -(C=O)-O-(C=O)- maleic anhydride fragment and the cyclohexene ring: In the endo conformation the MA fragment is at a 2.89Å distance to the "adjacent, opposite" -CH=CH- part of cyclohexene ring. In the exo conformation the MA fragment is 2.95Å away from the bridge -CH₂-CH₂- fragment on cyclohexene. The shorter distance in the endo-conformation could be due to stabilising secondary orbital overlap in this conformation between the C=O bonds on MA and the C=C of the ring. This also often referred to as the endo-rule and will be explained in the following section.

The relative instability of the exo-transition structure could be due to this through space relation between the the MA fragment and the ring-bridge as shown in the image. This distance is leass then 2x the typical VdW radius of a C-atom. The MA fragment and the bridge are within their VdW radius and hence there is a significant steric clash, which destabilises the exo-structure. Furthermore, in the exo-TS this steric clash is more significant since it is between sp₃ C of the bridge with 2 Hs, which are sterically more demanding, i.e. take up more space. In contrast to this in the endo-TS the steric interaction is between sp₂ C with only 1 H and hence there is less steric clash.

In short, the exo-adduct is disfavoured due to an increased steric strain relative to the endo-conformation. Plus, the endo-adduct is additionally stabilised by secondary orbital overlap.

Vibrational Frequency and Molecular Orbital Analysis of the Transition structures

Table 11: Analysis of exo- and endo-transition structures

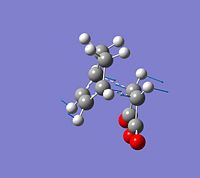
		Exo TS	Endo TS
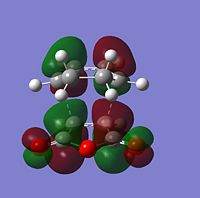
Molecular Orbitals	LUMO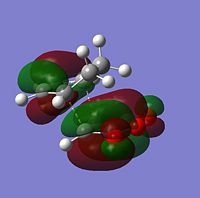
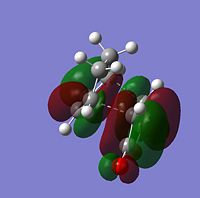	HOMO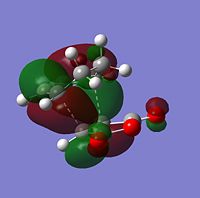
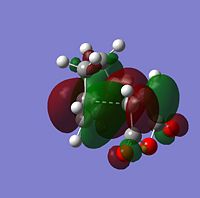Modes of Vibration	Imaginary Frequency / cm-1	-812.19	-806.38
	Visualisation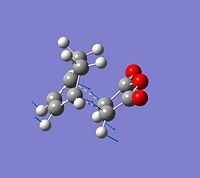

The symmetry of each MO was determined from looking at the nodes.....

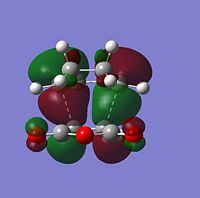The HOMO and LUMO of both TS structures are anti-symmetric with respect to the plane of symmetry of the compound. Based on the symmetry and energy arguments from the previous exercise, the HOMO of the transition state, essentially describing the new bonding interaction between the 2 terminal Cs of both conjugated systems, is formed from overlap of the HOMO of cyclohexa-1,3-diene and the LUMO (i.e.π* of the Maleic anhydride double bond). This HOMO LUMO interaction leads to the formation of 2 new σ-bonds.

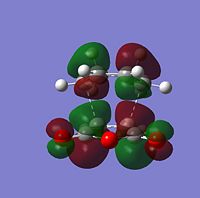
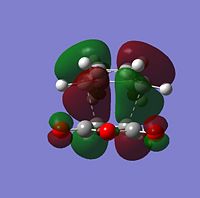
The sterochemistry of the final outcome can be explained by the endo-rule and secondary orbital overlap. The picture below shows the HOMO of the endo-TS geometry when the isovalue was reduced from 0.02 to 0.01. Secondary orbital overlap can be seen. The same was done for the HOMO of the exo-TS (isovalue=0.01), however no secondary orbital overlap was seen.

Transition state stabilisation in the endo-conformation

Real endo-TS-MO computed showing secondary orbital overlap

HOMO of the exo adduct

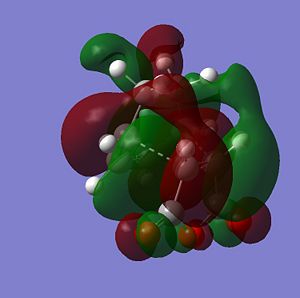In addition to the primary HOMO-LUMO overlap that essentially leads to the formation of the 2 new σ-bonds the transition state leading to the endo-conformer is stabilised by secondary orbital overlap. The bonding interaction at the back of the diene between the partial, delocalised π-system of the diene and the Carbonyl C=O π* orbital of the MA means additional stabilising interaction, which cannot take place in the exo-transition structure, since the MA fragment is pointing away from the conjugated π-system of the cyclohexadien. Due to this additional delocalised π-system across space the endo-TS is lower in energy. Therefore, the activation energy to get to the endo-transition state is lower and hence under kinetic control this is assumed to be the preferred reaction pathway.

Conclusion

Using these gaussian calculations the transition states of reactions can be accurately defined. Hence, this computational module showed how gaussian calculations cn be used to predict reactivity of a reaction not only in terms of the stability of the product, but also in terms of the activation energies. Therefore, this method can be used to investigate kinetically controleld reactions. Molecular orbitals were also computed to give a better idea of orbital overlap and hence provide even more information about the relative stability of different conformers. Three different methods were used and the advantages and disadvantages of each method were analysed and understood.