Rep:Mod3:kr207DA

The Diels Alder Cycloaddition

In this part the Diels Alder Cycloaddition and its reactivity was investigated using Gaussian transition state calculations. Further information on the bond forming and breaking process in the diels-alder reaction was obatined from analysis of molecular orbitals and vibrational frequencies computed. The Diels-Alder reaction is a pericyclic reaction and proceeds via a concerted mechanism, during which 2 or more σ-bonds are formed between the termini of 2 or more conjugated π-systems. In this exercise the HOMO-LUMO interaction of 2 reactants to form 2 new bonding-antibonding MOs was examined. It was then looked at the effect of substituents on the π-orbitals in terms of stabilising the regiochemistry of the main outcome of a DA reaction.

All calculations carried out were based on the AM1 semi-empirical molecular orbital method.

Ethylene and Cis-Butadiene

Diels-Alder reaction between cis-butadiene and ethylene

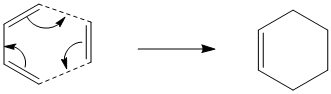
As can be seen this Diels Alder addition proceeds via a [4_πs-2_πs] concerted mechanism since there are 4π orbitals in the π system of butadiene and 2π orbitals on ethylene. This corresponds to a total electron of 6, which fits 4n+2 and hence, under thermal conditions, indicates a Hueckel topology transition sate with suprafacial components only.

To get a better idea of whether this reaction proceeds in a concerted stereospecific fashion, i.e. allowed, or not, i.e. forbidden, the MOs of the 2 reactants and the resulting transition state were computed.

Optimisation and Analysis of the reactants Ethylene and Cis-Butadiene

To begin with, butadiene and ethylene were optimised based on the AM1 semi-empirical method. This gave energies of 0.04879748Hartrees for cis-butadiene and 0.02619024Hartrees for ethylene, which corresponds to 30.620888kcal/mol and 16.434627kcal/mol, respectively.

Optimised Cis-Butadiene

Optimised Ethylene

A summary of the HOMO and LUMO of both reactants is shown in the table below. The symmetry of the MOs was determined with respect to the plane of symmetry as shown in the instructions for this module.

Table 8: FMOs of reactants

Reactant	Molecular Orbital	Visualisation		Energy / a.u.	Symmetry wrt the plane
Cis-Butadiene	LUMO			0.01712	Symmetric
	HOMO			-0.34386	Anti-symmetric
Ethylene	LUMO			0.05284	Anti-symmetric
	HOMO			-0.38777	Symmetric

The more nodes, i.e. ou-of-phase overlap in the MO, the higher the energy of the MO. Therefore the π-orbital of ethylene is lowest in energy and the π*-orbital of ethylene is least stable since it has anti-bonding interactions only. In constrast to this, the HOMO on cis-butadiene has more bonding that anti-bonding out-of-phase interactions and is therefore relatively stable. Also, the LUMO on cis-butadiene is close to non-bonding (i.e. close to 0a.u.) since anti-bonding and bonding interactions are close to cancelling each other out.

Optimisation and Analysis of the Transition State

Geometry of the guessed transition structure input

The transition state structure of this reaction was then computed and based on the AM1 semi-empirical orbital method. It was decided to use the force constant calculation. The settings for the calculation included: Opt+Freq, Optimisation to a TS(Berny), Calculate Force constant always, and in the additional keyword box: Opt=NoEigen to limit the calculation to one imaginary frequency. It was decided on this method, since we already roughly know what the transition state is expected to look like, namely with the ethylene approaching from above the plane. And the distance between the 2 termini of the conjugated systems was assumed to correspond to ≈2.1Å. If the guessed transition structure is good enough, this method is sufficient. The Frozen Coordinate method would be another option, however in this case the terminal distance is set to a fixed length, which limits the structural optimisation of the rest of the compound. Using this frozen coordinate method, it was found that a transition state with a very distorted cis-butadiene conformation was computed.





Vibrational Frequency Analysis
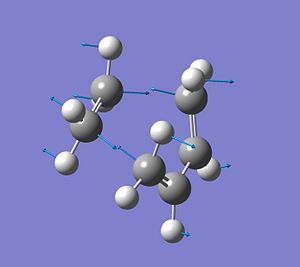
Vibrational analysis confirmed that the optimisation was successful. It was found that for this transition state there is one imaginary frequency at -955.47cm^-1, which corresponds to the vibration of the 2σ-bonds that are being formed during this reaction process. This indicates that a transition state has been optimised. From the displacement vecotors it can be seen that the imaginary frequency describes the synchronous formation of 2 bonds, i.e. the bond formation occurs at the same time. Furthermore, the next lowest possible frequency is at 147.47cm^-1 and corresponds to the rocking motion of the ethylene-Hs. There is no bond forming or bond breaking connected to this vibration. It shows that ethylene is not involved in the reaction pathway. It is simply a low energy vibration that therefore could take place at RT, since kbT is enough energy input to cause this vibration.

Imaginary vibration at -955.47cm-1

Low frequency vibration at 147.47cm-1

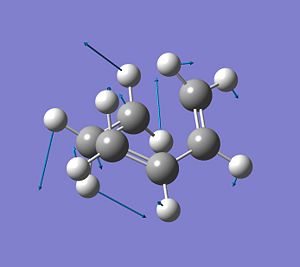Essentially, the frequency calculation is the second derivate of the potential energy surface, i.e. it describes the curvature of the potential energy vs r (bond distance). If a -ve frequency is found, this shows that we are a maximum of this PES curve, i.e. a high energy transition state has been optimised.

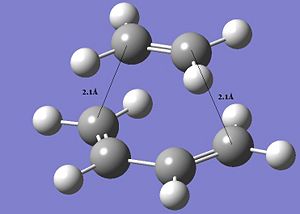
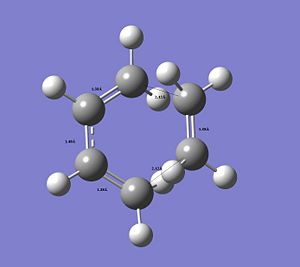
By measuring the CC bond distances in the transition state, further insight into the reaction mechanism can be obtained, as well as confirmation that the correct transtion state structure was optimised (please click on image to view bond distances).

C-C bond distances in the transition state

2D sketch of forming and breaking bonds

The typical sp³Carbon C-C single bond length is 1.54Å and the typical sp² Carbon C=C double bond length is 1.34Å. The fact that in this image as seen the C=C are longer compared to literature and the C-C single bonds as seen are shorter and in between the typical single and double bond distance confirms that a conjugated transition state was optimised with delocalised double bonds in transition from a double bond to a single bond or vice versa (see simple 2D image) with delocalised electron-density. The C=C double bonds as seen are in better agreement. The distance between the termini of the 2 conjugated systems is longer that a typical C-C single bond. However, the VdW radius of a C-atom is 1.71Å. This confirms the ongoing formation of the 2 new σ bonds forming between the ethylene and the cis-butadiene. The distance between the 2 termini between the reactants is shorter than 2 x the typical VdW radius of Carbon, which indicates that a bond is formed. The 2 termini Carbond atoms are close enough to each other to form a bond and share electron density. Since this is the transition state the bond has not actually been formed yet.
Also, as can be seen the bond distances in this transition structure are symmetrical. The 2 new, terminal distances are identical. This also indicates synchronous formation of the 2 new sigma bonds in the concerted reaction process. This synchronous bond formation of the 2 new sigma bonds in this DA cycloaddition was already confirmed by the vibrational analysis and the fact that only one imaginary frequency was obtained.
Molecular Orbital Analysis
In order to investigate the HOMO-LUMO interaction between the 2 reactants the HOMO and the LUMO of the transition structure were tabulated below.

Table 9: FMOs of Transition State

Molecular Orbital	Visualisation	Energy / a.u.	Symmetry wrt the plane
LUMO		0.02314	Symmetric
HOMO		-0.32394	Anti-symmetric

https://www.ch.imperial.ac.uk/wiki/images/0/06/TSDASIMPLEREPONEO_OPTFREQ.LOG

Comparing these MOs of the transition state to the reactant MOs it can be seen that the HOMO of the transition state if formed from the overlap of the HOMO of cis-butadiene and the LUMO of ethylene. This HOMO of the transition structure describes the bonding orbitals of the 2 new single bonds formed. This is consistent with the conservation of orbital symmetry in Diels-Alder cycloaddition. This describes the fact that the symmetry of the new orbital formed must be the same as the symmetry of the overlap of the orbitals it is derived from. In order to have significant overlap and thus form bonding MOs, the substituent orbitals must have sufficient electron density overlap, i.e. stabilising in-phase overlap. For this to be the case the reactant MOs must have the same symmetry. The LUMO of ethylene and the HOMO of butadiene are both anti-symmetric. This HOMO-LUMO pair interacts and give the anti-symmetric HOMO of the resulting transition state adduct, with 2 new sigma bonds.

Similarly, the LUMO is symmetric and formed from overlap of the substituent reactant MOs, namely overlap of the s HOMO from ethylene and the s LUMO from butadiene. This transition adduct LUMO describes the anti-bonding out-of-phase overlap along the 2 new bonds formed.

Both these HOMO-LUMO interactions have significant electron density overlap since they are of the same symmetry and therefore the reaction is symmetry-allowed. This also shows that orbital symmetry control determines the pathway of this reaction, at which the symmetry of the reactant and product MOs remain the same.REFFFF Conservation of orbital symmetry.

In addition, apart from the symmetry argument, the relative energies of the cis-butadiene HOMO-LUMO and the π-π* orbital of ethylene can be used to determine the HOMO of the transition structure. In order to achieve the best overlap and hence greatest stabilisation, both the symmetry has to match to have in-phase overlap, but also the relative energies of the substituent MOs. As can be seen from Table 8 the LUMO of the ethylene and the HOMO of the butadiene are closest in energy. Their energy difference is 248.933kcal/mol (vs 254.072 of the vice versa overlap), giving rise to the greatest stabilisation of the resulting bonding HOMO orbital in the transition state. This corresponds to the normal electron demand with the dienophile providing the LUMO and the diene providing the HOMO.

Cyclohexa- 1,3-diene and Maleic Anhydride

Diels-Alder reaction between Cyclohexa- 1,3-diene and Maleic Anhydride

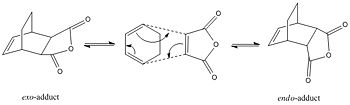
In this part the regioselectivity of the Diels-Alder reaction was examined and the effect of subsituents on the major outcome of the reaction was subseqeuently determined. This reaction is also a [4_πs+2_πs] concerted pericyclic cycloaddition. There is 6 conjugates π electrons in this reaction, which fits 4n+2. Subseqeuntly, under thermal conditions this reaction must proceed via a transition state in the Hueckel topology and all components mus react supraficially. Nevertheless, as seen in the sketch above this reaction can afford 2 diastereoisomers as product, the endo- and the exo-adduct. The primary product of the cycloaddition of cyclohexa-1,3-diene and maleic anhydride give the endo-adduct as primary product. Furthermore, as already discussed in module 1 this Diels-Alder cycloaddtion is assumed to be kinetically controlled, with the exo-transition state being higher in energy. In the following the transition states leading to both products were computed to examine this further and were then analysed using molecular orbitals computed.

Optimisation of the Transition Structures

The transition structure was optimised using the Force constant calculations. As previously, the calculations were based on the AM1 semi-empirical molecular orbital method. The following settings were selected: opt+Freq, Optimisation to a TS(Berny), and the force constant was calculated at every step (i.e. always), using the additional keywords:Opt=NoEigen in case the guessed structure is not good enough. Even though this method is the most expensive, it gives the most reliable result and the compound is not too large to use this method. An approximate transition structure was drawn in Gaussview: this input structure was then optimised manually first by changing the bond lengths, bond types and the dihedral angles. The structure was changed to be most symmetrical. It was cleaned and symmetrized several times, until a good guess of the particular transition structure was obtained. The distance between the 2 terminal C that form the 2 new σ bonds was estimated as 2.2Å. Particular attention was also paid to the positioning of the Hs, as shown in the Table below.

Table 10: Summary of exo- and endo-transition structures

	Exo TS	Endo TS
Input-orientation of Hs
Energy / a.u.	-0.05041985	-0.05150480
Energy / kcal/mol	-31.638940	-32.319757
Final structure	Taxol 11	Taxol 11

endo-TS DOI https://www.ch.imperial.ac.uk/wiki/images/c/c7/TSHUP_OPTFREQ.LOG exo-TS DOI https://www.ch.imperial.ac.uk/wiki/images/0/09/EXOTSDA_OPTFREQ.LOG

Analysis of the Transition Structures

The data obtained was then analysed to determine the regiochemistry of this reaction and relative stabilisation of the transition states.

Relative Energies of both transition states
Based on steric arguments the exo-product of this reaction is assumed to be the thermodynamic product, i.e. the most stabilised product due to reduced steric hindrance between the bridge and the maleic anhydride, since the Hs on maleic anhydride are pointing down in the exo conformation and thus steric clash is reduced. This steric clash in the endo-conformation is also referred to as 1,3-Diaxial Compression between the pointing up Hs on the ring-linkage and the Carbon bridge. This destabilising compression is reduced in the exo-conformation with the Hs on the other face of the ring.

Nevertheless, as mentioned at the outset the main outcome of this reaction is the endo-product, i.e. the higher energy kinetic product. Therefore, this reaction is assumed to be under kinetic control. In short, rather than the total energy, i.e. the stability of the product, the energy and hence stabilisation of the transition state controls the outcome of the reaction. The rate of the reaction, i.e. the activation energy barrier leading to the transition state determines the major product of this reaction.

From the optimisation calculations carried out above, the endo-transition structure was found to be more stable by 0.681kcal/mol. Therefore, the activation barrier is lower to get to the endo-transition state. Hence, the reaction pathway leading to the endo-transition structure and subsequently the endo-adduct, proceeds at a faster rate and the endo-adduct will be the major adduct under kinetic control and irreversible reaction conditions. The exo-transition structure leads to the exo-product formed under thermodynamic control.However, it has to be taken into account that this energy difference is not very significant since the inherent error of gaussian energy calculations is ≈5kJ/mol, which corresponds to 1.2 kcal/mol. This indicates one of the limitations of these Diels-Alder reactions.

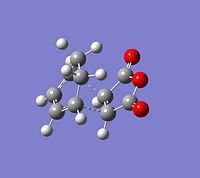
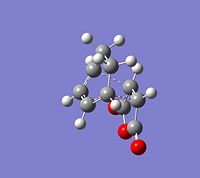
The following images show the CC distances in both transtition structures.

C-C bond distances in the endo-TS

C-C bond distances in the exo-TS

internal C-C bond distances in the endo-TS

internal C-C bond distances in the exo-TS

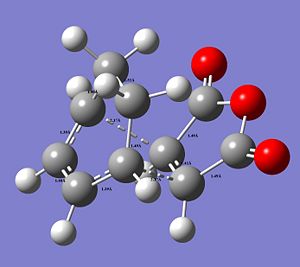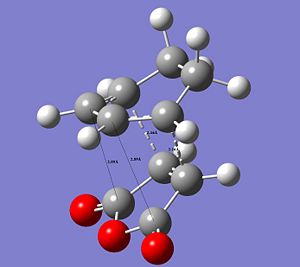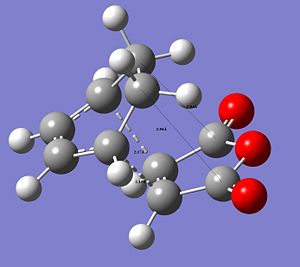The CCbond lengths are very similar in both structures as well as the length of the newly forming CC σ-bonds with 2.17 and 2.16Å. Similarly to the analysis of the bond lengths for the butadiene-ethylene transition state, here the developing and breaking double bonds have a similar length, in between the typical single and double bond length. The 2 terminal C in between the 2 new bonds are formed are close enough, i.e. < 2xtypical VdW radius of C-atoms, to allow bond formation. Particular attention can be paid to the through space interaction between the -(C=O)-O-(C=O)- maleic anhydride fragment and the cyclohexene ring: In the endo conformation the MA fragment is at a 2.89Å distance to the "adjacent, opposite" -CH=CH- part of cyclohexene ring. In the exo conformation the MA fragment is 2.95Å away from the bridge -CH₂-CH₂- fragment on cyclohexene. The shorter distance in the endo-conformation could be due to stabilising secondary orbital overlap in this conformation between the C=O bonds on MA and the C=C of the ring. This also often referred to as the endo-rule and will be explained in the following section.

The relative instability of the exo-transition structure could be due to this through space relation between the the MA fragment and the ring-bridge as shown in the image. This distance is leass then 2x the typical VdW radius of a C-atom. The MA fragment and the bridge are within their VdW radius and hence there is a significant steric clash, which destabilises the exo-structure. Furthermore, in the exo-TS this steric clash is more significant since it is between sp₃ C of the bridge with 2 Hs, which are sterically more demanding, i.e. take up more space. In contrast to this in the endo-TS the steric interaction is between sp₂ C with only 1 H and hence there is less steric clash.

In short, the exo-adduct is disfavoured due to an increased steric strain relative to the endo-conformation. Plus, the endo-adduct is additionally stabilised by secondary orbital overlap.

Vibrational Frequency and Molecular Orbital Analysis of the Transition structures

Table 11: Analysis of exo- and endo-transition structures

		Exo TS	Endo TS
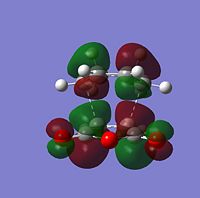
Molecular Orbitals	LUMO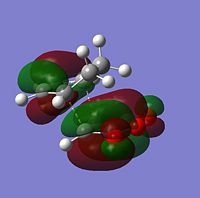
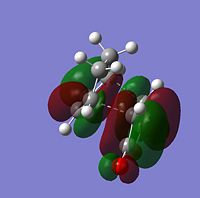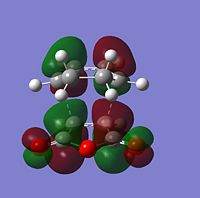
	HOMO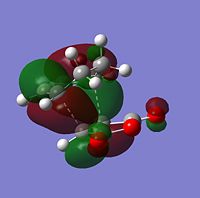
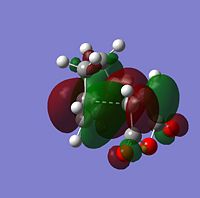Modes of Vibration	Imaginary Frequency / cm-1	-812.19	-806.38
	Visualisation

The symmetry of each MO was determined from looking at the nodes.....

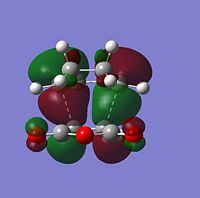The HOMO and LUMO of both TS structures are anti-symmetric with respect to the plane of symmetry of the compound. Based on the symmetry and energy arguments from the previous exercise, the HOMO of the transition state, essentially describing the new bonding interaction between the 2 terminal Cs of both conjugated systems, is formed from overlap of the HOMO of cyclohexa-1,3-diene and the LUMO (i.e.π* of the Maleic anhydride double bond). This HOMO LUMO interaction leads to the formation of 2 new σ-bonds.

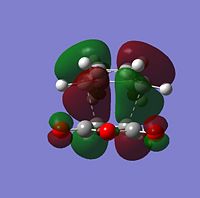
The sterochemistry of the final outcome can be explained by the endo-rule and secondary orbital overlap. The picture below shows the HOMO of the endo-TS geometry when the isovalue was reduced from 0.02 to 0.01. Secondary orbital overlap can be seen. The same was done for the HOMO of the exo-TS (isovalue=0.01), however no secondary orbital overlap was seen.

Transition state stabilisation in the endo-conformation

Real endo-TS-MO computed showing secondary orbital overlap

HOMO of the exo adduct

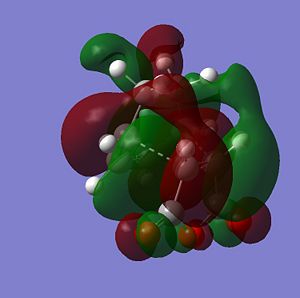In addition to the primary HOMO-LUMO overlap that essentially leads to the formation of the 2 new σ-bonds the transition state leading to the endo-conformer is stabilised by secondary orbital overlap. The bonding interaction at the back of the diene between the partial, delocalised π-system of the diene and the Carbonyl C=O π* orbital of the MA means additional stabilising interaction, which cannot take place in the exo-transition structure, since the MA fragment is pointing away from the conjugated π-system of the cyclohexadien. Due to this additional delocalised π-system across space the endo-TS is lower in energy. Therefore, the activation energy to get to the endo-transition state is lower and hence under kinetic control this is assumed to be the preferred reaction pathway.

Conclusion

Using these gaussian calculations the transition states of reactions can be accurately defined. Hence, this computational module showed how gaussian calculations cn be used to predict reactivity of a reaction not only in terms of the stability of the product, but also in terms of the activation energies. Therefore, this method can be used to investigate kinetically controleld reactions. Molecular orbitals were also computed to give a better idea of orbital overlap and hence provide even more information about the relative stability of different conformers. Three different methods were used and the advantages and disadvantages of each method were analysed and understood.