Module 3

The Cope Rearrangement

In this part, we will focus on the Cope rearrangement of 1,5-hexadiene to study and tackle some chemical reactivity problems. It is now generally accepted that this reaction can occur either via a chair or a boat transition structure, with the latter one having a higher energy. By investigating the different conformations of 1,5-Hexadiene, the minimum energy of each conformation will be found and compared so as to find the one with lowest energy.

Optimizing the Reactants and Products

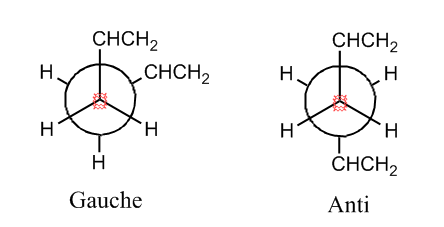
It is well known that 1,5-Hexadiene has two different conformations: Gauche and Anti. These are shown below in Newman projection:

Since there are a few possible orientations for the CHCH₂ groups, there are 6 Gauche conformers and 4 Anti conformers as shown in Appendix 1.

3 Gauche conformers and 3 Anti conformers were chosen to be analysed and compared with each other so as to check if the same result as Appendix 1 (Gauche 3 had the lowest energy) could be obtained through computational method: a conformation was drawn in GaussView and the structure was then cleaned before optimizaing using the Hartree-Fock calculation method with 3-21G as the basis set. A number of different Gauche and Anti confirmations were made and opitimised to find their lowest energy comfirmation and the energy of this comfirmation. The results and structures are shown below:

**Comparison Of The Different Conformers**
	Gauche 1	Gauche 3	Gauche 4
Images
Jmol
Point Group	C₂	C₁	C₂
RMS Gradient (Hartrees)	0.00000986	0.00000849	0.00000813
Dipole Moment (Debye)	0.4559	0.3407	0.1281
Energy (Hartrees) HF/3-21G	-231.68772	-231.69266	-231.69153
Relative Energy (kcal/mol)	3.10	0.00	0.71

**Comparison Of The Different Conformers**
	Anti 1	Anti 2	Anti 4
Images
Jmol
Point Group	C₂	C_i	C₁
RMS Gradient (Hartrees)	0.00005173	0.00004749	0.00000468
Dipole Moment (Debye)	0.2027	0.000	0.2955
Energy (Hartrees) HF/3-21G	-231.69260	-231.69254	231.69097
Relative Energy (kcal/mol)	0.04	0.08	1.06

The above table clearly showed that the result obtained by computational method agreed with the reference data from Appendix 1 that Gauche 3 was the conformation with lowest energy. However, the two larger CHCH₂ groups in Gauche conformations are always next to each other while being opposite to each other (furthest away possible) in Anti conformations and hence the former conformation should be higher in energy due the steric hindrance. The result of unexpected low energy in Gauche conformation can be explained by comparing the Highest Occupied Molecular Orbitals (HOMO) of Anti 1 and Gauche 3

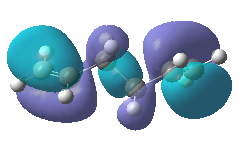
From the above HOMOs, we can immediately spot that there is orbital overlap between the pi orbitals of the two alkene in Gauche 3 conformation but not in Anti 1 conformation as the alkenes in Anti conformations are always furthest away from each other unlike Gauche confomations which have their alkenes closest to each other. This orbital overlap lowers the energy to a degree that overcomes the decrease in energy due to steric hindrance and makes the Gauche 3 conformation the most stable.

Since the Anti 2 comformation is expected to be the reactant when 1,5-hexadiene undergoes Cope rearrangement, after obtaining exactly the same values from Appendix 1, the conformation was then reoptimized at B3LYP level with a more complex 6-31G(d) as basis set. Structures and data of HF/3-21G calculations and the higher level of theory B3LYP/6-31G(d) were compared and shown in the table below:

**Comparison Of The Data obtained from 2 Different Computational Methods**
Energy Term	Hartree-Fock/3-21G	B3LYP/6-31G(d)
Images
Jmol
Point Group	C_i	C_i
RMS Gradient (Hartrees)	0.00004749	0.00005876
Dipole Moment (Debye)	0.000	0.000
Energy (Hartrees)	-231.69254	-234.61172

From the above table, it can be seen that both computational methods give very similar structural data and the more complex method B3LYP/6-31G(d) is better by being able to produce a lower energy and hence giving a more stable product.

Frequency calculations using different methods and conditions as follow: Hartree-Fock/3-21G, B3LYP/6-31G(d) (298K) and B3LYP, 6-31G(d) (0.001K) were run and the results were compared as below:

**Comparison Of The Data obtained from 2 Different Computational Methods**
Energy Term	Hartree-Fock/3-21G	B3LYP/6-31G(d) (298K)	B3LYP, 6-31G(d) (0.001K)
Sum of Electronic and Zero Point Energies	-231.5395	-234.4583	-234.4663
Sum of Electronic and Thermal Energies	-231.5326	-234.4526	-234.4663
Sum of Electronic and Thermal Enthalpies	-231.5316	-234.4518	-234.4663
Sum of Electronic and Thermal Free Energies	-231.5709	-234.4874	-234.4663
Energy (Hartrees)	-231.6925	-234.6117	-234.6095

From the above table, as mentioned before, the more complex method B3LYP/6-31G(d) is better by being able to produce a lower energy and hence giving a more stable product. We can also tell from above that for B3LYP, 6-31G d at 0.001K, except for total energy, all the energy values are the -234.4663 Hatrees. This is because at very low temperature (close to zero, the values for the Sum of Electronic and Thermal Energies, the Sum of Electronic and Thermal Enthalpies and the Sum of Electronic and Thermal Free Energies will equal the Sum of Electronic and Zero Point Energies value as these value will tend to zero as temperture tends to zero.

Optimizing the "Chair" and "Boat" Transition Structures

As mentioned before, the Cope Rearragement of 1,5-hexadiene occurs via either a "Chair" or a "Boat" transition state. Energies of the two possible transition states were found and compared in order to find out which one of the two is the preferred transition states for the Cope rearragement.

An allyl fragment was drawn and optimized using the HF/3-21G level of theory. The optimized allyl structure was then manipulated and the two fragments were oriented to roughly like the chair transition state before optimizing it manually in two different ways - the Force Constant Method and the Freeze Coordinate Method.

The first method was to optimize the structure to a TS (Berny) using the method Hartree Fock with basis set 3-21G.This structure was then optimised, but not to minimum, but to TS (Berny). This was done again using the Hatree-Fock calculation method and the 3-21G basic set. The force constants were calculated once and Opt=NoEigen was typed in Additional keyword so as to stop the calculation crashing if more than one imaginary frequency was detected during the optimization. The imaginary frequency vibration is shown below:

Table 6: Imaginary Frequency vibration of the Chair Transition State for the Cope Rearragment
Transition State	Frequency	Intensity	Vibration
Chair	-817.92cm^-1	5.9127

The other method was to freeze the distance between the two pairs of terminal carbons to be 2.2 Å of the guess structure. The structure was then optimized to minimum using the Hartree-Fock method with basis set 3-21G and it would then look the same as the optimized transition done above but the bond forming/breaking distances were fixed to 2.2 Å. This structure was then furhter optimized by using a normal guess Hessian modified to include the information about the positions of the two terminal carbons. The resulting structure of this optimisation for the stucture of Chair TS was the same as the structure obtained by the Force Constant Method. Energies of the two Chair TS formed by the two methods were shown and compared below:

**Comparison Of The 2 Different Computational Methods**
Methods	Force Constant Method	Freeze Coordinate Method
Images
Jmol
Point Group	C₁	C₁
RMS Gradient (Hartrees)	0.00003002	0.00002990
Dipole Moment (Debye)	0.001	0.000
Energy (Hartrees)	-231.6193	-234.6193
Sum of electronic and zero-point Energies (Hartrees)	-231.4667	-231.4667
Sum of electronic and thermal Energies (Hartrees)	-231.4613	-231.4613
Sum of electronic and thermal Enthalpies (Hartrees)	-231.4604	-231.4604
Sum of electronic and thermal Free Energies (Hartrees)	-231.4952	-231.4952

The above table shows that both methods produce optimized structures with same energies and hence both methods are valid.

After optimizing the Chair Transition State, the Boat Transition State was then optimized by using another method - QST2. In this method, transition state would be found by interpolating between the reactant and the product of the reaction via calculation. The reactant and the product were labelled based on the optimized Anti 2:

First TS(QST2) optimisation calculation was then run by using the Hartree-Fock method with basis set 3-21G. The resulting transition state structure is shown below:

The job failed as it looked like a disssociated chair TS rather than a boat TS. Only top allyl fragment can be translated by the calculation which does not consider the possibility of rotations around central bonds. Before retrying the TS(QST2) optimization calculation again, geometries of Reactant A and Product A were modified closer to the boat TS as shown below:

TS(QST2) optimization calculation was run again using the method of Hartree-Fock with basis set 3-21G and the resulting transition state structure and data are shown below:

**Boat Transition State**
Images
Jmol
Point Group	C_2V
RMS Gradient (Hartrees)	0.00002226
Imaginary Frequency	1
Dipole Moment (Debye)	0.1585
Sum of electronic and zero-point Energies	-231.4509
Sum of electronic and thermal Energies	-231.4453
Sum of electronic and thermal Enthalpies	-231.4444
Sum of electronic and thermal Free Energies	-231.4791
Energy (Hartrees)	-231.60280

Since it is known that there is one negative frequency vibration for a transition state which refers to the bonding/breaking in the reaction, the vibrations of the boat TS was checked to ensure the right conformation was found.

Table 6: Negative Frequency Vibration of Boat Transition State for the Cope Rearragment
Transition State	Frequency	Intensity	Vibration
Boat	-840.05cm^-1	1.6181

After finding the optimized chair and boat transition structures, Intrinisic Reaction Coordinate (IRC) method was used to follow the minimum energy path from a transition struction down to its local minimum on a potential energy surface. Since our reaction coordinate was symmetrical, only forward direction needed to be computed. The result of these calculations are shown below, as well as the comformation of 1,5 Hexadiene found by these calculations:

**IRC for Chair TS and Boat TS**
Conformation	Chair TS	Boat TS
Images
Jmol
Images

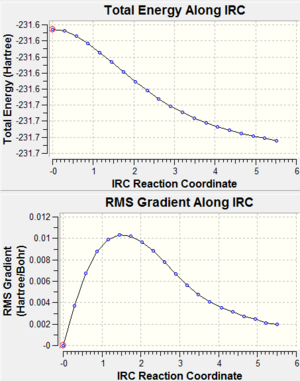From the above graphs, steep gradient at the end of the curve which is expected for a complete optimization cannot be found. This suggested that both graphs did not reach minimum energy conformations and hence the gradient was not zero. In order to find the minimum energy conformations, the IRC was redone specifying that the force constants were computed at every step this time. The new resulting conformations and calculations are shown below:

**IRC (every step) for Chair TS and Boat TS**
Conformation	Chair TS	Boat TS
Images
Jmol
Images

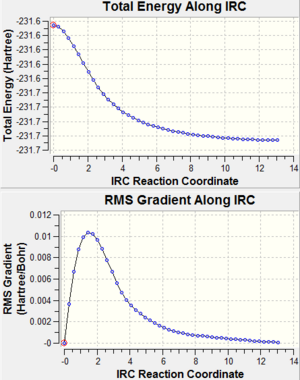From the above tables, it can be concluded that Anti 2 is the conformation of 1,5-Hexadiene that undergoes Cope rearrangement via Chair TS and Boat TS, showing the prediction above saying Anti 2 is the reactant is correct.

By comparing the geometries and energy differences between the reactant Anti 2 and the two transition states, we can eventually find out which one of the two transition states undergoes the Cope rearrangement. Both chair and boat transition states were reoptimized using B3LYP method with basis set 6-31G(d) in order to compare the calculation method combination results. It is also more computational efficient to map the potential energy surface using a low level of theory first and then reoptimize at a higher level like what we have done.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466686	-231.461329	-234.556887	-234.411559	-234.405086
Boat TS	-231.602802	-231.450926	-231.445296	-234.543093	-234.398506	-234.392578
*Reactant (anti2)*	-231.692535	-231.539539	-231.532565	-234.611723	-234.469203	-234.461856

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.72	44.70	36.17	35.62	33.5
ΔE (Boat)	55.61	54.76	44.36	43.47	44.7

From the above table, it is obvious that the Chair transition state is lower in activation energy than the Boat transition states which means Chair transition state undergoes the Cope rearrangement rather than the Boat transtion states. It can also be seen that the calculations and the activation energies for the more complex B3LYP/6-31G(d) method are closer to experimental value compared to the Hartree-Fock/3-21G method.

The Diels Alder Cycloaddition

Cis-butadiene reaction with ethene

For a Diels Alder Cycloaddition reaction to occur, the phase of the interacting orbital lobes must be the same and there must also be good orbital overlap between the pi-orbitals of the 2 reactants. In order to have this to happen, the symmetry of the HOMO and LUMO on the two reactants must be the same with respect to the plane run down the molecule. Computational method could be used to find the shape tand the symmetry of the molecular orbitals of molecules. The HOMO and the LUMO for Cis-butadiene and Ethene are shown below:

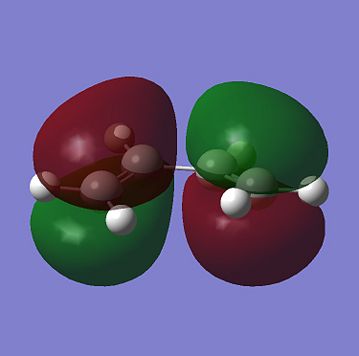
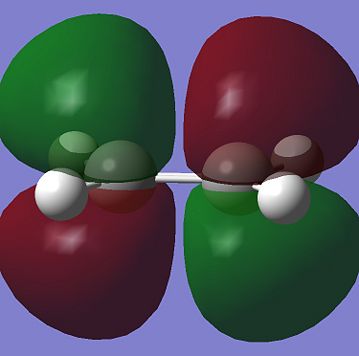
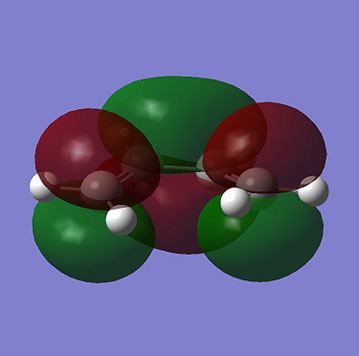
From the molecular orbitals above, it can be seen that both HOMO of Cis-butadiene and LUMO of ethene are anti symmetric with respect to a plane perendicular to C-C bond in the former and C=C bondin the latter while both LUMO of Cis-butediene and HOMO of Ethene are symmetric with respect to the same plane mentioned. These 2 pairs of orbitals could overlap as they are of the same phase and since this is HOMO-LUMO overlapping, the chemical reaction above is feasible. One of the two pairs will be the HOMO of the transition state of this reaction and the other pair will be the LUMO. In order to find out which pair correspnds to which MO of the transition state, a guess structure which was thought to be similar to the transition state was constructed and optimized to TS(Berny), using AM1 semi-empirical calculation method and calculate the force constant once only. The resultant structure is shown below:

In order to comfirm that the correct structure had been calculated, the negative frequency with the motions of bond formation were found and shown below:

Besides showing the bond formation, this vibration also tells that both the bonds forming are forming at the same time - synchronous. This vibration above does shown the formation of the bonds seen to be forming the reaction scheme of the Diels Alder cycloaddition seen above and comfirms the fact that the correct structure of the transition state has been calculated. The vibration given above also provides other information. It can be seen from the vibrataion above that both the bonds forming are forming at the same time, the bonds form synchronous. The lowest positive frequency vibration was also found to compare with the negative frequency:

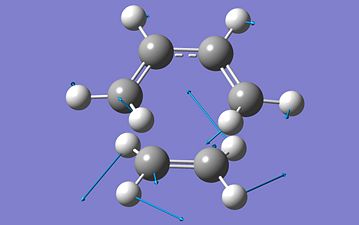
Lowest positive frequency at 145.28cm^-1

Unlike the negative bond forming vibration which is a stretching vibration, the lowest positive frequency vibration is a bending vibration. It can be seen that this vibration is a bending type of vibration, unlike the bond forming vibration which a stretching vibration. The bond formation is also symmetric and this can explain why the bonds form are synchronous while the lowest positive frequence vibration is antisymmetric and its vibration is small compare with the bond formation vibration.

The bond lengths of the partly formed σ C-C bonds are 2.21 Å which are much longer than the 1.54 Å ^[1] σ C-C bond distance but still within the sum of Van der Waals radius of carbon which is 3.4 Å. This shows that there is no actual interaction but there is still a bond, and this is what we called a transition state.

The shapes of the HOMO and LUMO transition state can be easily obtained by running the energy calculation. These are shown below:

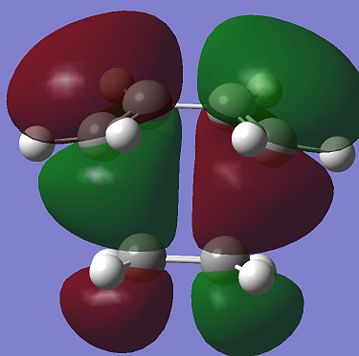
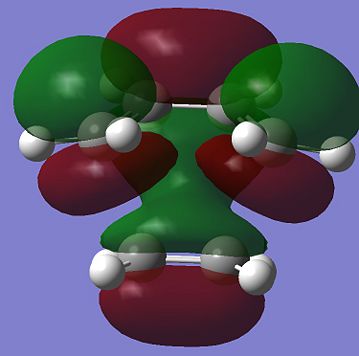
It can be easily found out that the the anti symmetric HOMO transition state is formed by HOMO of the cis-butadiene and LUMO of the ethene. On the other hand, the symmetric LUMO of the transition state is formed by the LUMO of the cis-butadiene and the HOMO of the ethene. Since the orbitals that are overlapping are all of the same phase and also because of good overlapping between the MOs of the reactants, the reaction is allowed to take place.

Cyclohexa-1,3-diene reaction with Maleic Anhydride

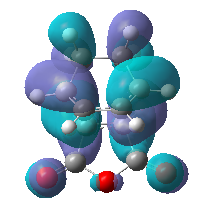
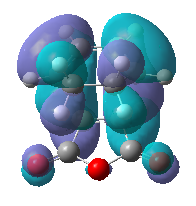
For this reaction, either exo or endo product will be formed. In order to investigate whether the exo transition state is higher in energy or the endo transition state, guess structures of both transition states were constructed and were optimized to TS (Berny) using the method AM1 semi-empirical and the force constants were only calulated once. The resulting strucetures of transition states are shown below:

To ensure we obtain the correct structure, the negative bond forming vibration was checked if it was presence in the structure. This check was done on both Exo TS and Endo TS and the following motion of vibration was snapshot and shown below:

Negative frequency vibration for the Exo TS at -812.28cm^-1

Negative frequency vibration for the Endo TS at -805.81cm^-1

As there is only one negative frequency found in each transition states which both of them correspond bond formation so both are the correct structure from the calculations but still this doesnt help us finding which one is the main product. So, the energy data of both transition states was tabulated and shown below for comparison:

Table 9: Comparing energy valuhod (All values in Hartrees)
Energy Term	Exo TS	Endo TS es calculated for the Exo TS and the Endo TS using the AM1 Semi-empiral calculation met
Sum of Electronic and Zero Point Energies	0.1349	0.1335
Sum of Electronic and Thermal Energies	0.1449	0.1437
Total Energy	-0.0504	-0.515

From the table above we can see that clearly Exo transition states, leading to Exo product has a higher energy than the Endo one and this is why the Endo product is the major product of the reaction and is under kinetic control. But why is endo lower in energy than exo TS?

One charateristic which many explain the energy difference between the Exo TS and the Endo TS is the bond lengths and the distance between the O=C-O-C=O unit and the -CH₂-CH₂- unit in the Exo TS and the distance between the O=C-O-C=O unit and the -CH=CH- unit in the Endo TS. These two pairs mentioned are bulky group and so the shorter the distance between them, the higher the energy of transition state. The distance for these lengths for both the Exo TS and Endo TS are shown below for the different calculation methods and basic sets:

Table 12: Comparing structural parameters calculated using the AM1 Semi-empirical method for Exo TS and Endo TS
Structural Parameter	Exo TS	Endo TS
Distance between two bulky groups	3.35Â	3.32Â
C-C Forming bond length	2.17Â	2.17Â
C-OC Bond length	1.41Â	1.41Â
C=C Bond length (Double bond braking)	1.39Â	1.39Â
C=C Bond length (Double bond forming)	1.40Â	1.40Â

We can see from the above table that all the distance of the two transition states are the same except the one we mentioned above, the distance between the two bulky groups and as Endo TS has a smaller distance between the two bulky groups, it should have a higher energy rather than lower energy as proved above, so there must be some other reasons that can overcome this steric hindrance.

The maleic anhydride fragment is situated almost parallel and next to the cyclohexa-1,3-diene in the endo product, whereas in the exo product is situated away from the diene. We would expect the endo product to be higher in energy and less favourable due to the steric hindrance between the diene fragments and the -(O=C)-O-(C=O)- fragment of the anhydride as mentioned above. However there exists a secondary orbital overlap between the two groups in the endo product which is not possible in the exo product. This overlap stabilises the product, and most importantly, the stabilisation overcomes the destabilisation from the steric hindrance. Hence the endo product is the major product of the reaction.

References

↑ Stark, J. G.; Wallace, H. G., Chemistry Data Book, London, 2001

[1] Stark, J. G.; Wallace, H. G., Chemistry Data Book, London, 2001

[1]