Computational lab Module 3

Cope Rearrangement

The Cope rearrangment[1] reaction is a [3,3]-sigmatropic rearrangment reaction, which occurs via a single concerted cyclic transition state.

Optimizing the Reactants and Products

Part (a)

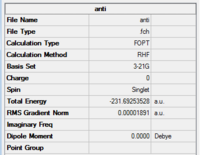
For the anti conformation, the point group is found to be C_i. By comparing the energies and symmetry of the molecule to data in Appendix 1, the optimised structure is identified to be anti2.

Part (b)

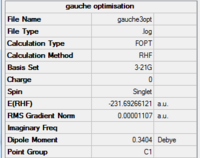
For the gauche conformation, the point group is found to be C₁. By comparing the energies and symmetry of the molecule to data in Appendix 1, the optimised structure is identified to be gauche3.

Making comparison between the structure of anti2 and gauche3, we would expect gauche1 to be the less stable conformer as there are larger steric hindrance, thus repulsions within the structure. Yet this is proven to be wrong from the calculation, where the electronic energy is lower for gauche3 (-231.69266121 a.u.) than anti2 (-231.69253528 a.u.). This result can be explained by the stereoelectronic effect, where the п orbital of the C=C interacts with the σ*C-H orbital of the adjacent vinyl proton and stabilse the gauche conformation.

Part (c)&(d)

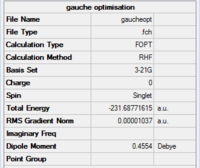
As mentioned above, the energy of the conformer is a balance of both steric and stereoelectronic factors, where the stereoelectronic factor has a larger contribution to stablility. Therefore, we would expect gauche3 to be the most stable structure. This is proven by producing the other gauche structure for comparison.

**Table 1: Summary of the gauche and anti structures of 1,5-hexadiene optimised**
Conformer	Energy / a.u.	Point Group	file on D-space
anti2	-231.692535	C_i	http://hdl.handle.net/10042/to-5612
gauche3	-231.692661	C₁	http://hdl.handle.net/10042/to-5614
gauche5	-231.689616	C₁	http://hdl.handle.net/10042/to-5616
gauche4	-231.691530	C₂	http://hdl.handle.net/10042/to-5615
gauche1	-231.687716	C₂	http://hdl.handle.net/10042/to-5613

Comparing the different conformation, gauche3 has the lowest electronic energy of -231.692661.

Part (e)

The anti2 conformer is optimised in previous section, the data are provided above.

Part (f)

The anti2 conformer is re-optimised using a more accurate basis set (DFT/B3LYP/6-31G*). Comparison is made between the two sets of result in the table below.

Table 2: Optimisation of Conformers

molecule

Pentahelicene

Basis set

HF/3-21G

B3LYP/6-31G*

File Type

.log

Calculation Type

FOPT

Calculation Method

RHF

Final Energy / a.u.

-231.692535

-234.611703

RMS Gradient Norm / a.u.

0.00001891

0.00001326

Dipole Moment / Debye

0.0000

Point Group

C₁

Output file

http://hdl.handle.net/10042/to-5612

http://hdl.handle.net/10042/to-5617

Most data remained the same from a better basis set theory. However, the final energy of the molecule lowered by around 3 a.u. when the anti conformer is re-optimised, indicating that the structure is further optimised to a lower energry state.

**Table 3: Comparison of geometric data obtained for anti2 using 2 different basis sets**
Basis set used	Bond length/ Angstroms and Torsional angle / °
Basis set used	C1-C2,C5-C6	C2-C3,C4-C5	C3-C4	C2-C3-C4-C5	C1-C2-C3-C4	C6-C5-C4-C3
HF 3-21G	1.32	1.51	1.55	180.0	114.7	114.7
B3LYP 6-31G*	1.33	1.50	1.55	180.0	118.5	118.5

In terms of geometry, the molecule has not change significantly, the torsional angle increased by around 4 degrees, while the bond length shifted by around 0.01 angstroms. Making comparison with the literature values( lit: C=C is 1.34 angstroms and C-C is 1.54 angstrom), the simulated bond lengths are in agreement with the value.

Part (g)

A frequency analysis is carried out on the re-optimised anti2 structure. There are no imaginary vibration frequency in the result and the IR spectrum is shown below:

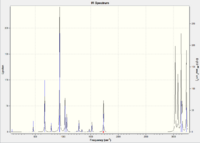No imaginary vibration indicating that the structure optimised at the previous step is at its minimum.

An optimisation at 0K was also carried out, the thermochemistry data of the two frequency analysis are shown in the table below:

Table 4 - Thermochemistry data from frequency analysis of 6-31G(d)-optimized 1,5-hexadiene
	Analysis at 298.15K	Analysis at 0K
Final energies / E_h	-234.611703 a.u.	-234.611703 a.u.
Sum of electronic and zero-point energies / E_h	-234.469212 a.u.	-234.468774 a.u.
Sum of electronic and thermal energies / E_h	-234.461856 a.u.	-234.461429 a.u.
Sum of electronic and thermal enthalpies / E_h	-234.460912 a.u.	-234.460485 a.u.
Sum of electronic and free energies / E_h	-234.500821 a.u.	-234.500371 a.u.
Output file	http://hdl.handle.net/10042/to-5619	http://hdl.handle.net/10042/to-5620

The (electronic)final enegry at both temperature remained the same, but the other sums increase in energy as temperature decrease to 0K.

Optimizing the "Chair" and "Boat" Transition Structures

The transition state of the Coper rearrangement can be adopt either a chair or a boat configurations. In this section, we would analysis the different between the two ts in further details.

Part (a)

An allyl fragment (CH2CHCH2) is optimised using the HF/3-21G level of theory. Using this fragment, a guess transition structure is produced.

Part (b)&(c)&(d)

Optimisation of the guess transition state structure (TS Berny) was carried out using HF/3-21G basis set, followed by an frequency analysis. The result showed a imaginary vibration at -817.95 [[1]]

The same calculation with ModRedundant Minimisation which frozen C-C lengths, at 2.20 Å, for the C atoms involved in bond breaking/forming was then carried out. There is a imaginary vibration at -818.01 [[2]]

The data of the two calculation are listed below:

Force Constant

Redundant Coordinate

Structure

Pentahelicene

C-C bond length within allyl fragments (Å)

2.02

Final Energy (a.u.)

-231.61932247

-231.61932204

RMS Gradient (a.u.)

0.00000829

0.00005617

Spin

Singlet

Charge

0

Dipole (D)

0.0000

Point Group

C_2h

Frequency of Imaginary Vibration (cm^-1)

-818

output file on D-space

http://hdl.handle.net/10042/to-5627

http://hdl.handle.net/10042/to-5626

Using redundant coordinate method, we obtained a lower final energy ie. a better optimised structure. the point group, dipole and the imaginary vibration remained the same.

Part (e)

For the optimisation of the boat transition state, we are using a different method known as QST2. QST2 involve the coordinates of the starting product and reactants, and from that deduce the transition state.

Opt+Freq job was run with a basis set of HF/3-21G. However, the first job failed to give the right transition state geometry:

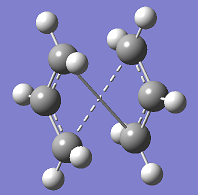
Output file on D-space: http://hdl.handle.net/10042/to-5636

This is due to the readily rotation of the central C-C bond. The starting structure is too different from the expecting product. Therefore,for the second time, the bond angles and torsion angles are adjusted before the optimisation, and the QST2 successful produce the boat transition state:

Pentahelicene

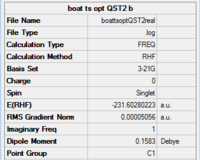
There is an imaginary bond breaking vibration at -840.08, therefore this is a asynchronous bond formation.

Part (f)

Despite the fact that we obtained the transition state geometry of both chair and boat, we cannot fom that deduce the geometry of the final product. Intrinsic Reaction Coordinate (IRC) calculation is therefore used to model the transformation from chair transition state down the potential energy surface to the final product of the reaction. The method was applied twice to the chair ts. The first time having it to calculate the force constants once, and the second time at every single steps. The latter method provide a better result, this can be demonstrated by the IRC energy curve where the latter method reaches closer to the minimum. This is also reflected by the energy of the structure, where the latter method is around 0.026 a.u. lower. From the energy and the point group of the IRC final structure, we can deduce that the chair ts leads to the formation of the Gauche2 conformer.

**Table 5: Summary of IRC calculations for the chair transition state**
	Calculate Force Constants Once	Calculate Force Constants always
Points along IRC	20	47
IRC energy pathway & RMS gradient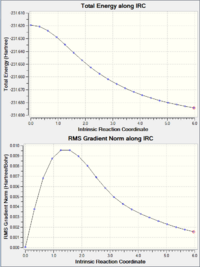
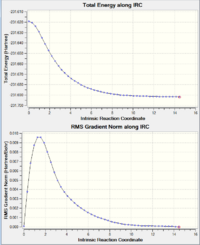
Final structure of IRC
Energy / a.u.	-231.68409949	-231.69166411
point group	C₂	C₂
out put file on D-space	http://hdl.handle.net/10042/to-5624	http://hdl.handle.net/10042/to-5625

Part (g)

Optimisation and frequency analysis were carried out to both boat and chair ts, at different temperature(298.15k and 0K) and usinfg different basis set (HF/3-21G and B3LYP/6-31G*). The thermochemistry data of the result are shown below, in comparison with the anti2 values:

**Table 6: Thermochemistry Data of the chair and boat transition structures**
	HF/3-21G			B3LYP/6-31G*
	Electronic energy / a.u.	Sum of Electronic and zero point energies at 0K / a.u.	Sum of Electronic and thermal enthalpies at 298.15K / a.u.	Electronic energy / a.u.	Sum of Electronic and zero point energies at 0K / a.u.	Sum of Electronic and thermal energies at 298.15K / a.u.
Chair Transition State	-231.619322	-231.466224	-231.461341	-234.556983	-234.414485	-234.409008
Boat Transition State	-231.602802	-231.450456	-231.445301	-234.543093	-234.401903	-234.396008
Reactant anti2	-231.692535	-231.539069	-231.532565	-234.611703	-234.468774	-234.461856

From the data above, the activation energy of the boat and chair transition reaction are calculated:

**Table 7: Summary of acitvation energies**
	HF/3-21G		B3LYP/6-31G*		Experimental Data
	at 0K	at 298.15K	at 0K	at 298.15K	at 0K
ΔE Chair	45.71	44.69	34.07	33.16	33.5 +/- 0.05
ΔE Boat	55.61	54.76	41.96	41.32	44.7 +/- 2.0

The activation energies match well with literature values at 0K. The activation energy for chair ts is lower than the Boat ts, suggesting that the reaction via chair ts is a preferred pathway.

The Diels Alder Cycloaddition

Diels Alder reaction

In this section, we are looking at the diels alder cycloaddition between butadiene and ethylene. The molecular orbital are simulated for both the reactants and the transition state.

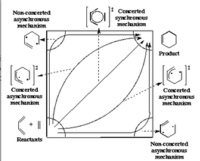
The reaction transition state are consider to be either synchronous or asynchronous. It can either be concerted, bond breaking followed by bond formation, or vice versa. This is shown by the diagram on the right.

part (i)

The structures of both ethylene and butadiene are optimised and their molecular orbital are simulated using semi-empirical AM1 basis set.

Interacting Molecular Orbitals of Ethylene and cis-Butadiene

Structure

HOMO

LUMO

Energy / a.u.

cis-Butadiene

Pentahelicene

HOMO:-0.34380 LUMO:0.01707

Ethylene

Pentahelicene

HOMO:-0.38775 LUMO:0.05284

Looking at the molecular orbital, we would expect interaction to occur between the HOMO of butadiene and the LUMO of the ethylene. The same assumption is made by looking at the energy of the orbital(ethyleneLUMO-butadieneHOMO = 0.05284-(-0.34380)= 0.39664 and butadieneLUMO-ethyleneHOMO = 0.01707-(-0.38775) = 0.40482), where the orbitals of ethylene LUMO and butadiene HOMO are closer in energy. This agrees with our knowledge that the diene is acting like an electron acceptor, while the ethylene being the donator.

Part (ii)

The transition state of the Diels Alder cycloaddition are produced using the QST2 method. QST2 was chosen over the TS(Berny) method as QST2 requires less step while providing a higher success rate in obtaining the correct transition structure.

Pentahelicene

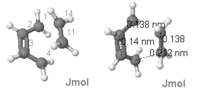The bond length of the transition state are listed below:

Table12: Geometry of Transition State
Bond	Bond length / Å
C1-C2	1.38
C2-C3	1.40
C3-C4	1.38
C4-C11 Bond forming	2.12
C11-C14 Ethene bond	1.38
C14-C1 Bond forming	2.12

Typical values of the Csp3-Csp3 bond length is 1.53 Å, and the unconjugated Csp2-Csp2 bond length is 1.48 Å^[1]. These are slightly different from the calculated result.

The literature Van der Waals radius of a carbon is 1.70Å^[2].. The distance between the bond forming carbon is 2.12Å, indicating that the atoms are approaching within their Van der Waals radii. However, 2.12Å is still longer than a normal C-C single bond,and the bond is not fully formed in the transition state.

lowest real frequency vibration of the TS

HOMO of the Transition State - Antisymmetric

LUMO of the Transition State - Symmetric

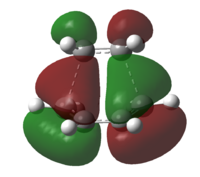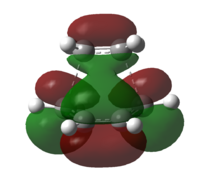The imaginary vibration at -956cm^-1 indicates the bond formation vibration, and the motion of the vibration is synchronous. This suggest that the Diels-Alder reaction is a concerted reaction. The rocking motion of the lowest positive frequency vibration at 147cm^-1 is asynchronous.

Looking at the orbital of the transition state, we can identify that the HOMO is correspond to the interaction between the LUMO of ethylene and HOMO of butadiene, whereas the LUMo of the transition state correspond to the interaction between the HOMO of ethylene and the LUMO of butadiene.

A better basis set (DFT/B3LYP/6-31G* method) was used to re-optimise the transition structure.

The two set of data is shown below:

*Table 5: Energy of TS*
Properties	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)
Electronic Energy / a.u.	0.111655	-234.543896
Sum of Electronic and Zero-Point Energies / a.u.	0.253275	-234.403321
Sum of Electronic and Thermal Energies / a.u.	0.259452	-234.396903
Sum of Electronic and Thermal Enthalpies / a.u.	0.260397	-234.395959
Sum of Electronic and Thermal Free Energies / a.u.	0.224014	-234.432887
Imaginary Frequency / cm^-1	-956	-525
C-C Bond Forming distance / Å	2.12	2.27
Output file on D-space	http://hdl.handle.net/10042/to-5637	http://hdl.handle.net/10042/to-5638

part (iii)

In this section we study the reaction between Cyclohexa-1,3-diene and maleic anhydride. The reaction can result in two different products, it can either be an exo form or an endo form. The molecular orbitals and transition states structure are simulated below for further investigation energies of the reaction.

Molecular Orbitals of Ethylene and cis-Butadiene

Structure

HOMO

LUMO

Energy / a.u.

maleicanhydride

maleicanhydride

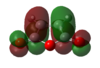HOMO:-0.44185 LUMO:-0.05952

Cyclohex-1,3-diene

Cyclohex-1,3-diene

HOMO:-0.32074 LUMO:0.01692

Optimisation of Transition State

Exo TS
AM1

Endo TS
AM1

transition state

maleicanhydride

Energy / Hartree a.u.

-0.050503

-0.051594

Sum of electronic and
thermal energies / Hartree

0.14479

0.14359

Imaginary Frequency / cm^-1

-811.47

-805.32

Output file on D-space

http://hdl.handle.net/10042/to-5640

http://hdl.handle.net/10042/to-5639

Comparing the transition state of both exo and endo structure, the endo is lower in energy. As the reaction is a irreverisble, thus kinetic control dominates, endo structure would therefore be the primary product of the reaction between maleicanhydride and cyclohex-1,3-diene. Exo is more strained as steric hindrance between the oxygen from the maleicanhydride and the hydrogen on the sp3 carbon is larger than in endo, where the sp3 carbons are replaced by sp2, one hydrogen less.

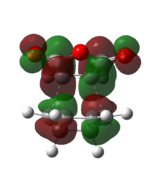
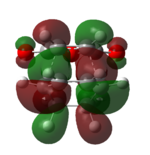
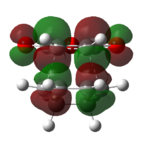
Endo TS		Exo TS
HOMO (-0.34506 a.u.)	LUMO (-0.03570 a.u.)	HOMO (-0.34275 a.u.)	LUMO (-0.04044 a.u.)

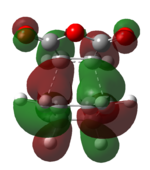
Anti-symmetric	Anti-symmetric	Anti-symmetric	Anti-symmetric

Both the HOMO and the LUMO of the endo and exo transition state are antisymmetric. If we compare the HOMO and LUMO of the transition states to the reactants'. We can identify that the reaction only involve the interaction between the Cyclohex-1,3-diene HOMO and maleicanhydride LUMO.

Secondary orbital interactions is only observed in the endo HOMO, the π*C=O orbital are in the same phase as the π conjugated system in the cyclo-1,3-hexadiene, thus an interaction between the orbitals at the back of the molecule stabilise the endo transition and giving large overlap between the orbitals of the bond forming carbons, indicating a favourable bonding interaction.^[3]

Reference

↑ F.H. Allen, O. Kennard, D.G. Watson, L. Brammer, A.G. Orphen, R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1-S19: DOI:10.1039/P298700000S1
↑ A. Bondi, J. Phys. Chem., 1964, 68, 441: DOI:10.1021/j100785a001
↑ R. Hoffmann, R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388: DOI:10.1021/ja00947a033

[BL-1] F.H. Allen, O. Kennard, D.G. Watson, L. Brammer, A.G. Orphen, R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1-S19: DOI:10.1039/P298700000S1

[Bondi-2] A. Bondi, J. Phys. Chem., 1964, 68, 441: DOI:10.1021/j100785a001

[Hoffmann-3] R. Hoffmann, R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388: DOI:10.1021/ja00947a033

[1]

[2]

[3]