Rep:Mod3:hgiaffar

Module 3 - The Transition State

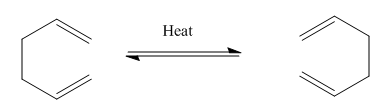
The Cope rearrangement

The Cope Rearrangement is characterised as a [3,3]-sigmatropic reaction; as this reaction is pericyclic in nature it necessarily proceeds in a concerted manner through a single cyclic transition state.

For 1,5 cyclohexadiene, the reaction occurs as below

Interestingly, this particular reaction is also known as the Narcissus Reaction (for obvious reasons).

Optimisation of the Conformers pertaining to 1,5-hexadiene

The modelling and subsequent optimisation of this particular reaction will make use of Gaussian and will be based on the Hartree-Fock and Density Functional Theory methods.

Optimisation under HF (3-21G)

Optimisation of selected conformers of 1,5-hexadiene

Property	Anti1-Conformer	Anti2-Conformer	Gauche3-Conformer
Final Energy / a.u.	-231.69260235	-231.69253529	-231.69266
Point Group	C2	Ci	C1
Molecule	anti-1	anti-2	Gauche

Chemical intuition would suggest that the unfavourable steric interactions between neighbouring carbon based groups would raise the Energy of the gauche conformer relative to the corresponding anti one. The results of Dr. Bearpark's analysis would show this to be incorrect (at least in the limit of his scope/accuracy), giving the gauche-3 conformer as relatively speaking, the most stable one.

The origin of this stability has been identified as electron density from the pi(C=C) orbital of each of the alkene groups into the adjacent sigma* (C-H) orbtal on an adjacent proton.

A frequency calculation was run to check that the local minimum had been reached in each case; no imaginary frequencies were detected, and so it was concluded that each structure had been optimised to a minimum.

Comparison between the Optimisation of the anti-2 conformer using DF/B3LYP/6-31G* and HF/3-21G

The anti-2 conformer was further optimised using the DF/B3LYP/6-31G*, this was done in the hope of refining the structure gained in the first round of optimisation. The majority of the geometric parameters remained virtually unchanged under the second optimisation operation (with both sets in good agreement with the literature); one noticable exception to this was the dihedral angle between C1 and C4 (arbitrarily labelled because of symmetry) - this increased by three degrees upon reoptimisation. This reoptimisation also yielded a more stable conformer (a more negative energy). Again, a frequency analysis was carried out on optimised geometry (under DF/B3LYP/6-31G) in order to be certain that this was still a local minimum, and therefore the relevant ground state. A frequency analysis was again run on this optimised structure, with no imaginary frequency present indicating that a minimum had been reached.

Comparison of the parameters of the optimised conformers

Method/Basis Set	HF/3-21G	DFT/B3LYP/G-31G
Point group	Ci	Ci
Molecule	anti-1	anti-2
Final Energy / a.u.	-231.692535	-234.611711
Calculated Dihedral Angle	115	118
C=C bond length	1.32	1.32
sp2C-sp3C bond length	1.51	1.51
C-C bond length	1.55	1.55
C1-C2-C3 angle	124.6	125.3
C2-C3-C4 angle	112.3	112.2

From the log file the energy of the molecule can be separated into potential and kinetic energy parts and from there the enthalphy and free energy of dissociation can be calculated. These parameters are temperature-dependent and so a calculation was run at 0 K as well as 298K to study the effect of temperature on the various energies, the results are tabulated below:

The Energy of the molecule can be further analysed, giving the individual contributions of a number of thermodynamic parameters:

Energies / a.u.	298.15K
Zero-point correction	0.14251
Thermal correction to E	0.14985
Thermal correction to S	0.15080
Thermal correction to G	0.11093
Sum of electronic and zero-point Energies	-234.46922
Sum of electronic and thermal Energies	-234.46191
Sum of electronic and thermal Enthalpies	-234.46092
Sum of electronic and thermal Free Energies	-234.50078

Optimisation of the 'Chair' and 'Boat' Transition State Structures

Optimisation of the 'Chair' Transition State

The TS to the chair molecule was built using two allyl fragments. The optimisation of this structure was done using the HF/3-21G basis set and following two different methods. The first of these was an Opt+Fre calculation, optimising to a TS (Berny). The second, so called 'frozen-coordinate' method, froze the bond forming/breaking lengths at 2.2 Angstroms, and performed a energy optimisation on the resultant constrained configuration.

TS (BERNY) METHOD – this method works very well if the geometry of the TS is reasonably well understood. The method relies on calculating a Hessian Matrix of force constants in the first instance of optimisation, and then continually recalculating the Matrix as the optimization proceeds (The PES is traversed). When using this method, the additional keyword ‘opt=NoEigen’ was added to prevent the calculation stopping if an imaginary frequency is found (essentially what is being looked for).

FROZEN COORDINATE METHOD - The optimization of the constituent fragment molecules is first necessary when using this method; after that, the appropriate bond forming/breaking distances are set as ‘frozen’ (in this case the distance between the terminal carbons was set at 2.2Å), and the molecule is optimised. The molecule is then ‘unfrozen’ and optimised again. This method does not require the calculation of the whole Hessian Matrix, and so is more efficient in terms of computer time.

Comparison of the results yielded by the two Optimisation Techniques

Properties	Opt+Fre	Frozen Coordinate
Energy / a.u.	-231.619328320	-231.61931910
Imaginary Frequency / cm-1	-818	-818
Animated Vibration	opt+fre

Both optimisation methods yielded the same imaginary frequency and bond lengths. Also, to a good degree of accuracy, both methods give the energy of the transition state as -231.619 au. The bond vibration with imaginary frequency of 818ch^-1 corresponds to the asynchronous formation of the bond (concerted pericyclic Cope reaction). The bond/forming breaking length was also mutually calculated as 2.017 Angstroms

Optimisation of the 'Boat' Transition State

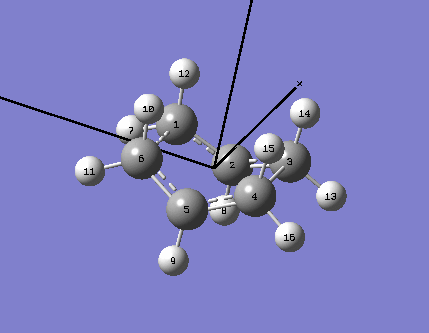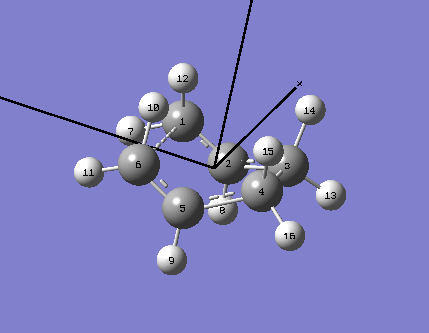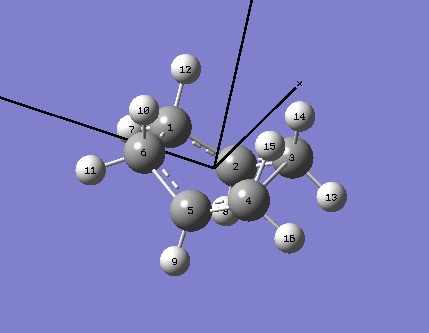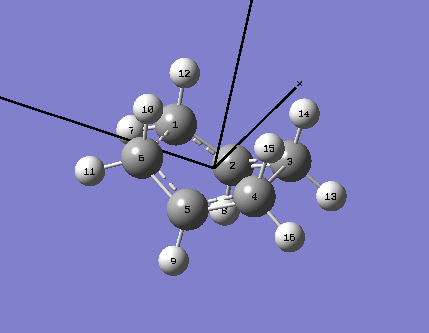
This optimisation was performed using a different method; the QTS2 optimisation required the input of the reactant and product molecule in the same screen, as well as for each atom to be labelled (this is done according to the following scheme):

The numbering of the atoms on both the reactant and product was very important when using this method, and corresponded exactly to that shown below;

boat transition state

Calculated parameters for the Boat TS

Properties	QST2
Final Energy / a.u.	-231.60282
Imaginary Frequency / cm-1	-840
C-C Bond Breaking/Forming Length / Å	2.14

A single imaginary frequency at -840cm-1 would indicate that a TS was found; the vibration corresponding to this is illustrated below (the asynchronous nature of the vibration fits well with what is known of the mechanism in the Cope reaction – a concerted electrocyclic reaction).

Intrinsic Reaction Coordinate Results

Predicting the product from the chair and boat transition states is not immediately possible; using the IRC method allows an examination of the local environment around the transition state on the Potential Energy Surface. This method follows a succession of small steps in the molecular geometry in the direction of the steepest gradient of the energy surface - this will lead to the local energy minimum. The fck file for the optimised chair transition state structure was altered, with the IRC option selected, the reaction coordinate was computed in the forward direction as the reaction retains symmetry. The force constants were calculated only once in the first instance, and then always during the second optimisation.

When the force constants were calculated once, the results indicated that the reaction was incomplete (the IRC indicated that a minimum on the potential energy surface was not reached). The method that relied on the force constants always being calculated resulted in the formation of the expected bond, and therefore -1,5-hexadiene (supported by evidence from the IRC pathway; which reached an asymptote at zero).

Comparison of IRC calculations for the chair structure with the force constants calculated once and always

	Calculated force constants once	Calculated force constants always
Final number of points along IRC	24	47
Final Structure using the IRC method
Energy / a.u.	-231.68906923	-231.69199434
Energy Change - calculated with 'once and 'always'	2.92511 x 10-3 a.u	7.68 KJ mol-1
IRC pathway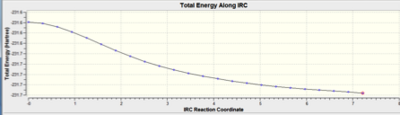
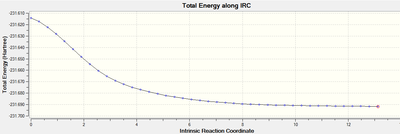
IRC gradient

Comparison of the Optimised Chair and Boat Transition States

The Transition State as described by the HF/3-21G optimised structure were not sufficient and so were re-optimised under a TS (Berny) opt+freq calculation using the DFT/B3LYP/6-31G method.

The results of a comparison of the structure and energy pertaining to each of the chair and boat TS at 298.15K, are shown below.

Table 5: Comparison of Chair and Boat TS

Properties	Chair TS at 298.15 K	Boat TS at 295.15 K
Electronic Energy / a.u.	-234.55698	--234.54309
Activation Energy / a.u.	0.052812	0.065834
Activation Energy / kJ mol-1	33.10	41.4
Literature Activation Energy / kJ mol-1	33.5 ± 0.5	44.7 ± 2.0
Imaginary Frequency / cm-1	-565	-504
C-C Bond Breaking/Forming Length / Å	1.97	2.20
TS Structure	chair	Tsboat
Vibration Corresponding to the Imaginary Frequencies /cm -1

Activation Energies of the Transition States

The following evidence supports the assertion that the B3LYP/6-31G* level of theory is more accurate; in both instances it gives an activation energy closer to the Literature value than the HF/3-21G method (The results for the Chair TS are closer than for the Bot TS). The Chair TS is the more stable, and so it can be assumed that the Cope rearrangement goes through this transition state.

Calculated Activation Energies for the Chair and Boat Conformers

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Literature
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
Energy Change - Chair (kcal mol-1)	45.71	44.70	34.04	33.15	33.5 ± 0.5
Energy Change - Boat (kcal mol-1)	55.59	54.76	41.94	41.31	44.7 ± 2.0

The Diels-Alder Cycloaddition

The Diels-Alder reaction has been classified as a [4+2] cycloaddition between a syn(Z,Z)-diene and a dienophile; the reaction falls into the pericyclic area of chemistry (TS stablised by an additional aromatic character) and is concerted with no intermediate species. It is the number of π-electrons that are directly involved in the pericyclic TS that determines whether the reaction is allowed (i.e. goes in a concerted stereospecific fashion) or forbidden (does not). The calculations were run using the semi-empirical/AM1 method, and were further ratified (in the last step by) by the DFT/B3LYP/6-31G method.

Cycloaddition of cis-butadiene and ethene

This reaction is the basis for understanding DA reactivity, and

Optimisation of the Reagents

An Opt+Freq calculation was run on the guessed structure using the semi-empirical/AM1 method, with a frozen bond length between the DA termini of 2.2Å. When this had been produced, two separate Opt+Freq calculations were run on it using the TS (Berny); the first using the semi-empirical/AM1 method and the other using the DFT/B3LYP/6-31G. The QMTS2 method was not chosen due to the necessary laborious preparation of the molecule for analysis.

Optimisation of cis-Butadiene

Energy	Energy / a.u.
Electronic Energy / au	0.0491
Structure	cisbutadiene

Optimisation of ethene

Energy Type	Energy / a.u.
Electronic Energy / au	0.0314
Structure	cisbutadiene

MO's of the Optimised reagents

'

Reagent	Molecular Orbital	Gaussview	Symmetry w.r.t the plane	Energy a/u
cis-butadiene	LUMO		Symmetric	+0.017
cis-butadiene	HOMO		Anti-symmetric	-0.343
ethene	LUMO		Anti-symmetric	+0.052
ethene	HOMO		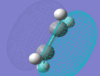Symmetric	-0.387

As orbital symmetry must be conserved (central to MO theory), the reaction can only proceed by interaction of the complementary HOMO/LUMO orbitals. This is seen perfectly in this reaction as the frontier orbital symmetry for cis-butadiene are exactly opposite to those for ethene;

Optimised Energy of the Transition State

Results of the Optimisation of the Transition State

	semi-empirical/AM1 method	Energy / a.u.	Imaginary Frequency / cm-1	Animated Frequency
Structure		0.10745	-419.41

MO's of the Calculated Transition State

Molecular Orbital	Gaussview	Symmetry w.r.t. the plane	Energy / a.u.
LUMO		Symmetric	+0.023
HOMO		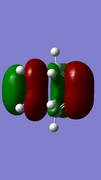Anti-symmetric	-0.323

Cyclohexa-1,3-diene reaction with maleic anhydride

The above example of a DA cycloaddition is probably the archetypal reaction in the class, however it offers the opportunity to study analogous systems which overall often have a far more complex orbital geometry. One such reaction is that between Maleic Anhydride and Cyclohexa-1,3-diene; this will be studied in detail in the following analysis, and proceeds according to the following reaction scheme:

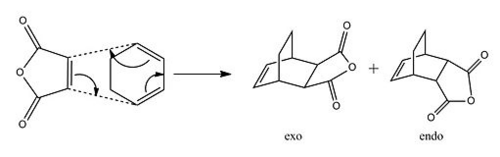
The ratio of formation of the diastereomeric products depends largely on the stereoselective basis of this reaction, and will be discussed in view of the orbitals generated for the Transition State.

Optimised Parameters

The Two guess structures for the transition state were drawn on Gaussview and were then subjected to an Opt+Freq calculation using the semi-empirical/AM1 method discussed above, again the bonds were frozen at 2.2Å between the respective carbons. Producing a reasonably guess structure seemed to be very difficult in this instance, but was eventually managed, the results are shown below:

Comparison of the exo and endo transition states of the cycloaddition reaction

-	exo	endo
	Semi-empirical/AM1	Semi-empirical/AM1
Structure
Energy (a. u)	-0.05041925	-0.0515001
C-C bond forming length (Å)	2.17	2.11
Imaginary frequency (cm-1)	-619.14	-514
Animation

The IR spectra of the molecules have been included, with the top - exo and the lower - endo;

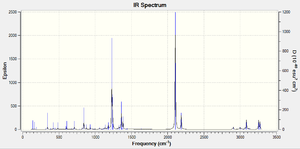
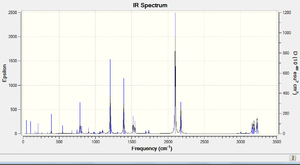
The fact that a single imaginary frequency was found for each structure confirms the nature of the optimised structure as TS, again the asynchronous nature of the vibration is in accordance with what would be expected for a bond forming cycloaddition. The Stereochemical reasoning for the stability of the endo TS will be discussed later (sterics would outwardly favour the exo TS due to a relatively lesser clash and 1,3 diaxial compressions).

Comparison of the Frontier Orbitals for the exo and endo transition states

Endo TS		Exo TS
HOMO	LUMO	HOMO	LUMO
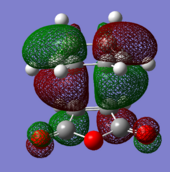
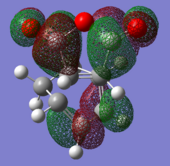
(-0.24230 a.u.)	(-0.06771 a.u.)	(-0.12445 a.u.)	(-0.32612 a.u.)
Anti-symmetric w.r.t. plane	Anti-symmetric w.r.t. plane	Anti-symmetric w.r.t. plane	Anti-symmetric w.r.t. plane

Activation Energy for the Reaction

The reactants were further optimised at the DFT/B3LYP/6-31G level of theory and the resultant (final) Energies were as follows:

cyclohexa-1,3-diene: -233.41892372 a.u. Maleic Anhydride: -379.28954454a.u.

The activation energies were taken from the sum of the energies is -612.70846830a.u, and are shown below;

Activation Energy	endo	exo
Activation Energy / a.u.	0.02507145	0.02968640

This equates to an Activation Energy in kJ mol^-1 of 65.8kJ mol^-1 for the endo product and 78.5kJ mol^-1 for the exo.

This calculation shows the strength of the computational approach taken, with the final results corroborating the theory; the activation energy for the endo transition state is significantly lower than that of the exo product, indicating a lower activation barrier and hence faster progression through the Transition state.

Concerning Stereoselectivity in Diels Alder Reactions

Traditionally, selectivity in this particular reaction has been attributed to an application of either the endo rule (after Alder) or by considering the secondary orbital interactions, which are governed by the Woodward-Hoffman Rules.

The former states that the the maximum accumulation of unsaturated centers leads to the most stable (lowest energy) transition state, and hence a more rapid progression through this particular phase on the PES, and eventually to an (in this case) almost exclusive product when under kinetic control (with the DA reaction being under kinetic control)

A consideration of the orbital interactions during the Transition state of the endo and exo cycloaddition indicates that there is an additional favourable interaction in the case of the endo addition; as well as the primary constructive overlap between the system termini (HOMO of the electron donor, and LUMO of the electron acceptor) - an interaction present in both forms of the reaction, there exists a secondary favourable donation of electron density from the region of the central carbons (in this case, in the cyclohexadiene) in the HOMO, and the π*_C=O orbital (on the maleic anhydride).

This above analysis was laid out by Woodward and Hoffmann in their groundbreaking study; the validity of their argument can be seen by applying the central tenets to the computer generated MOs of the Transition State.

Conclusion

This investigation has shown that the computational approach to quantitatively understanding a Transition State can be very successful. Using the TS (Berny) Optimisation method, the progression of a pericyclic reaction through the Transition state can be modeled convincingly; the calculated energies can be used to determine an activation energy, which when combined with a knowledge of the kinetically controlled nature of such reactions, (gained from experiment) can predict the major product from the possible range of stereo- and regio-isomers.