Rep:Mod3:gzus
Module 3: The Transition State
This experiment involves the study of transition structures in larger molecules. There are no longer fitted formulae for the energy, and the molecular mechanics and force field methods that work well for structure determination cannot be used as they do not describe bonds being made and broken or changes in bonding type or electron distribution. Instead, we can use molecular orbital-based methods, numerically solving the Schrodinger equation and locating transition structures based on the local shape of a potential energy surface. As well as showing what transition structures look like, reaction paths and barrier heights can also be calculated.
The Cope Rearrangement

The Cope Rearrangement can be used to locate the low-energy minima and transition structures on the C6H10 potential energy surface, to determine the preferred reaction mechanism. This [3,3]-sigmatropic shift rearrangement has been studied for a long time and its mechanism (concerted, stepwise or dissociative) was the subject of some controversy. It has been accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy. The B3LYP/6-31G* level of theory has been shown to give activation energies and enthalpies which are in good agreement with experiment. These will be calculated using Gaussian and are reported in the section below.
Optimising the Reactants and Products
The optimization of the the different conformations of 1,5-hexadiene were obtained in Gaussian and the point group for each of the structures were found. The vibrational frequencies and correct potential energies were calculated and visualized in order to compare them with experimental values. Two conformations of 1,5 hexadiene were initially formed with GaussView, one with anti arrangement whilst the other with a gauche arrangement and both optimized using the HF/3-21G method. These two stable conformations contained three different conformations which were compared with the ones in the Appendix Table 1, comparing energies and point groups respectively. The preliminary calculations are shown in the table below.
It can be seen that the lowest energy confirmation of 1,5 Hexadiene is the Gauche 3 confirmation. This is an unexpected result as Gauche confirmations are normally higher in energy compared to Anti confirmations due to the steric interactions between the two larger groups, which are next to each other in a Gauche confirmation and opposite each other in the Anti confirmation.
The Anti 2 confirmation of 1,5 hexadiene is considered to be the starting conformation when the molecule under goes a Cope rearrangement. In order to obtain more information, a further optimisation was performed on this structure using the complex B3LYP method with the 6-31G d basic set. The difference in energies predicted from both methods were apporximately 2000 kJ/mol, and is due to the complexity and accuracy of the basis sets used.
Other calculations were performed to obtain additional data that can be compared to experimental observations. This includes the sum of electronic and zero point energies (Electronic energies and vibrational at 0K), sum of electronic and thermal energies (Electronic energies and vibrational at 298K), sum of electronic and thermal enthalpies (sum of electronic and thermal energies with enthalpy correction) and sum of electronic and free energy energies (sum of electronic and thermal energies with entropy correction). These values can be used to give predictions of energy changes for a reaction and can be compared with experiments. These 4 values are shown below, along with total energy, as calculated by the different calculation method and basic sets:
| Energy Term | Hartree-Fock, 3-21G | B3LYP, 6-31G d (298K) | B3LYP, 6-31G d (0.001K) |
|---|---|---|---|
| Sum of Electronic and Zero Point Energies | -231.539 | -234.469 | -234.466 |
| Sum of Electronic and Thermal Energies | -231.533 | -234.462 | -234.466 |
| Sum of Electronic and Thermal Enthalpies | -231.532 | -234.461 | -234.466 |
| Sum of Electronic and Thermal Free Energies | -231.571 | -234.501 | -234.466 |
| Total Energy | -231.693 | -234.612 | -234.610 |
As can be seen from above, the energy values for the B3LYP, 6-31G d (0.001K) method are almost equivalent except for the total energy. This is expected as the temperature is close to zero so the values for the Sum of Electronic and Thermal Energies, the Sum of Electronic and Thermal Enthalpies and the Sum of Electronic and Thermal Free Energies will equal the Sum of Electronic and Zero Point Energies value. The results for the anti-optimisation can be seen here The results for the gauche-optimisation can be found here
Optimising the "Chair" and "Boat" transition structures
Introduction
This section is focused on setting up a transition state optimisation. This will be done by computing the force constants at the beginning of the calculation, using the redundant coordinate editor and using QST2. The reaction coordinate for the "chair" and "boat" structured transition states of the Cope rearrangement will be visualised and its activation energies calculated.
The Cope Rearrangement may proceed though a "Chair" or "Boat" Cyclohexane Transition State. In order to find out which of the two possible transition states the Cope rearrangement undergoes, the energies of the two possible transitions states have to be found and compared. There is a number of ways that the possible transition state can be optimized in order to find the energy of their lowest energy confirmations and these are demonstrated below.
Calculations
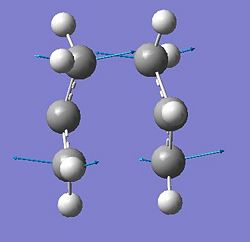
The first method is to build a structure that is approximately like the predicted transitions state and then optimise its structure as a transition state calculating the force constants in the molecule once, knowing that a transition state has one imaginary frequency (negative frequency on a vibration spectrum). This method was used to find the optimized structure Chair TS, using two allyl fragments optimised to their lowest energy confirmations with the Hartree-Fock calculation method and the 3-21G basis set.
This structure was then optimised to transition state (Berny) agian using the Hartree-Fock calculation method and the 3-21G basic set. The structure is similar to that given in appendix 2 and shows an imaginary vibration at -818cm-1.
 |
 |
Another method similar to the optimisation method above, is the "freeze coordinate" method. Again, the approximate structure for the Chair transition state as shown above was used, but this time instead of calculating force constants in order to optimise the Chair transition state structure to it lowest energy conformation, the distance between the two pairs of terminal carbons were frozen. The structure was then optimized to its minimum conformation, using the Hartree-Fock method with the 3-21G basic set. The resulting structure was completely optimized apart from the two bonds that are forming/breaking. This structure was used to calculate the structure of the Chair transition state by optimising the two bonds that are forming/breaking. This was done by performing an optimisation on the structure to TS (Berny) telling the calculation to derive the bond lengths between the two pairs of terminal carbons. This was done using again the Hartree-Fock method and the 3-21G basic set. Instead of calculating the force constants in the calculation as was done above in the previous method,a guess Hessian method is used to gain information about the positions of the terminal carbons. The resulting structure of this optimisation for the structure of Chair TS was the same as the structure shown above.
| Force Constant Method | Freeze Coordinate Method | |
|---|---|---|
| Energy (Hartree) | -231.619 | -231.619 |
| Gradient on the Energy Surface (Hartrees) | 0.00003 | 0.0000109 |
| Sum of Electronic and Zero Point Energies (0K) | -231.468 | -231.468 |
| Sum of Electronic and Thermal Energies (298K) | -231.4628 | -231.4628 |
Looking from the table of results above, both methods seem to give the same energy values and agree with each other, showing that both methods can be used.
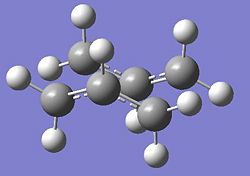
The Boat Transition state for the Cope rearrangement was found by using the QST2 method. Below is given the reactant and product for the Cope Rearrangement based on the Anti 2 confirmation of 1,5 Hexadiene.
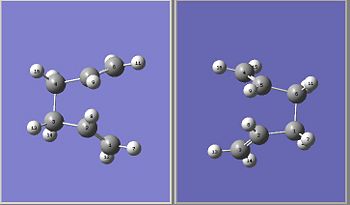
We can see the different energies of the chair, boat and anti structure all summarised in the table below.
| HF/3-21G | B3LYP/6-13G(d) | |||||
|---|---|---|---|---|---|---|
| Molecule | Electronic Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies |
| Chair Transition state | -231.619 | -231.468 | -231.461 | -234.557 | -234.415 | -234.409 |
| Boat Transition state | -231.6028 | -231.451 | -231.445 | -234.402 | -234.394 | |
| Anti2 | -231.69253 | -231.539540 | -231.533 | -234.612 | -234.469 | -234.462 |
The values computed in the table are in good correlation with the results given in the appendix. The difference in energy between the anti2 state and the boat transition state is larger than that of the chair transition state and implies the chair structure to be more stabilised.
The Diel's Alder Cycloaddition
Introduction
The Diels Alder reaction belongs to a class of reactions known as pericyclic reactions. The π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene. Whether or not the reacoccur in a concerted stereospecific fashion (allowed) or not (forbidden) depends on the number of π electrons involtions ved. In general the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. The nodal properties allow one to make predictions according to the following rule: If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed. The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden. If the dieneophile is substituted, with substituents that have π orbitals that can interact with the new double bond that is being formed in the product, then this interaction can stabilise the regiochemistry (i.e. head to tail versus tail to head) of the reaction. The nature of the transition structure for the Diels Alder reaction will be studied for both the prototypical reaction for the case where both diene and dieneophile carry substituents, and where secondary orbital effects are possible. The factors that control the nature of the transition state are quantum mechanical in origin and thus we shall use methods based upon quantum chemistry.
Reaction of cis-butadiene with ethene
GaussView was used to build cis butadiene and its geometry optimised using Gaussian, which can be found here. The HOMO and LUMO for cis-butadiene were then obtained by using the frequency file(here) and the symmetry for both were determined with respect to the plane. Below are both the HOMO and LUMO with their respective symmetries.
 |
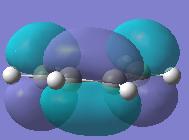 |
 |
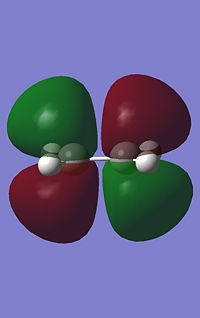 |
It can be seen that for this reaction to occur, there must be good orbital overlap between the pi-orbitals on both the cis-butadiene and the ethene molecule. The phases of the orbital lobes interacting must be equivalent for both (i.e. positive with positive, negative with negative). For this to occur, the symmetry of the molecular orbitals interacting (HOMO and LUMO) on the two molecules must be the same with respect to the plane run down the molecule. To find the shape the molecular orbitals of molecules and hence find their symmetry, computer calculations can be carreid out when the structure of the molecule is being optimized and will give the shape of the molecular orbitals.
The transition structure has an envelope type structure, which maximizes the overlap between the ethylene π orbitals and the π system of butadiene. The starting geometry of the transition strucutre was found by building the bicyclo system and then removing the allyl fragment. The interfragment distance was repeatedly guessed and the structure optimized.
From the molecular orbitals above, both the LUMO of Cis-butadiene and HOMO of Ethene are symmetric with respect to a plane perpendicular to the carbon-carbon single bond in the former and the carbon-carbon double bond in the latter. These orbitals could overlap with the correct phases and the chemical reaction could occur. The same is true if we consider the HOMO of the Cis-butadiene and the LUMO of the Ethene. Both of these orbitals are anti-symmetric with respect to the same plane described above and can overlap with the same phase, allowing the reaction above to take place. However, one of these two pairs of molecular orbitals (LUMO of Cis-butadiene/HOMO of Ethene and HOMO of Cis-butadiene/LUMO of the Ethene) will form the HOMO of the transition state of this reaction and the other pair will form the LUMO of the transition state. Knowing which molecular orbitals in the reactants results in which molecular orbital in the transition state is imperitive as in a reaction where more than one isomer can form,it may help determine which product will predominate by considering the orbital overlap between reactants and in the transition state.
In order to answer the question posed above (which reactant orbitals results in which orbitals in the transition state of the Diels Alder reaction given above), first the confirmation of the transition state has to be found. This was done by building a structure in the computer interface which was thought to be close to that of the transition state and then this structure was optimised to a TS Berny, using the AM1 Semi-Empirical calculation and calculating the force once. The resulting structure is shown below (and File:DA optimised TS gz.mol here)
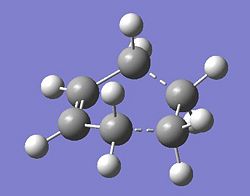
Reaction of Cyclohexa-1,3-diene with Maleic Anhydride
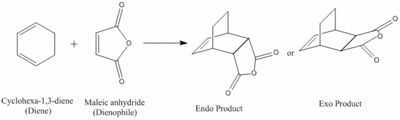
Cyclohexa-1,3-diene 1 undergoes facile reaction with maleic anhydride 2 to give primarily the endo adduct. The reaction is supposed to be kinetically controlled so that the exo transition state should be higher in energy. It is known that the exo product is lower in energy, but the major product of this reaction is the endo product. This suggests that this reaction is under kinetic control and that the energy of the transition to the endo product is lower than the transition state leading to the exo product.
To explore whether the exo transition state (Exo TS) is higher in energy than the endo transition (Endo TS) state, an approximate structure of both the possible transition states were built into the computer interface and were optimised to TS Berny, calculating the force constants once and using the AM1 Semi-empirical calculation method. The resulting structures of the transition states are shown below.
The main difference between the Exo and Endo transition states is that in the Exo form the-C(O)-0-C(O) group in the maleic anhydride is opposite a -CH2-CH2- in the cyclohexadiene ring, whilst in the Endo form the -C(O)-0-C(O) group in the maleic anhydride is opposite a -CH=CH- in the cyclohexadiene ring. This structural difference is important when considering the energy difference between the two transition states.
The two transition states were further optimised by optimising to TS Berny and calculating the force constants once, but using the Hartree-Fock calculation method and 3-21G basic set, and the energies for this optimisation are shown in teh table below.
| Energy Term | Exo TS | Endo TS |
|---|---|---|
| Sum of Electronic and Zero Point Energies | 0.1349 | 0.1195 |
| Sum of Electronic and Thermal Energies | 0.1449 | 0.1298 |
| Total Energy | -0.0504 | -0.0528 |
Analysing the data in the above table, we can confirm that the transition state leading to the Exo product is higher in energy than the transition state leading the Endo product, explaining why the Endo product is seen as the major product of the reaction. The reaction is thought to be under kinetic control however, these results do not explain why the Endo form is lower in energy than its Exo counterpart.
One way which may help explain the energy difference between the both forms is to look at the bond lengths and the distance between the O=C-O-C=O and -CH2-CH2- units in both the endo and exo forms. This distance is of great importance as it is the distance between the two large groups. The shorter the distance between them, the greater the steric hinderence causing the energy of the transition state to increase. The distance for these lengths for both the Exo TS and Endo TS are shown below for the different calculation methods and basic sets.
| Structural Parameter | Exo TS | Endo TS |
|---|---|---|
| Distance between large groups | 3.32Â | 3.29Â |
| C-C Forming bond length | 2.16Â | 2.17Â |
| C-OC Bond length | 1.41Â | 1.41Â |
| C=C Bond length (breaking) | 1.337Â | 1.339Â |
| C=C Bond length (forming) | 1.338Â | 1.341Â |
From the table above, we can see there is more steric hinderance in the Endo transition state than in the Exo transition state. This is shown by the the distance between two large groups is shorter in the Endo form than the exo form according to the calculations above. This would suggest that the Endo form should be higher in energy, but this is not the case and the Exo form is higher in energy. However,the two hydrogen atoms point towards the -C(O)-O-C(O)- group; the distance between them is 2.42Â as calculated by the AM1 Semi-emprical method. It is possible that there could be a sterc interaction between them, raising the energy of the Exo TS.
 |
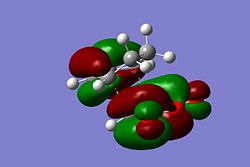 |
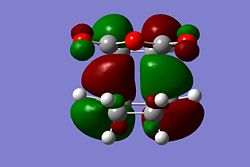 |
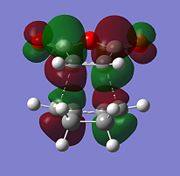 |
The HOMO of both transition states appear to be very similar and show no strong secondary molecular overlap, although in the HOMO of the Endo form, it can be seen there is possible overlap between the orbital on the -C-O-C- and the -CH=CH- orbital. However, if this was a particularly strong overlap the molecular orbital would be continuous. Here it is assumed that the method and the basis set used has little effect on the energy of the Endo transition state and therefore the HOMO for the Exo and Endo forms show very little secondary molecular orbital overlap. The energy difference of the two transition states would most likely to be due to steric interactions between the two hydrogens on the cyclohexadiene and the -C(O)-O-C(O)- on the Maleic Anhydride, causing the Exo transition state to be higher in energy than the Endo transition state.