Rep:Mod3:gohsiwei

Cope Rearrangement

The Cope rearrangment reaction is a [3,3]-sigmatropic rearrangment reaction.

As with other sigmatropic rearrangments, the reaction occurs via a single cyclic, concerted transition state in which one σ bond is formed while another is broken simultaneoulsy in a conjugated п systems.

1,5-hexadiene undergoes the reaction shown below.

In this exercise, Pople's Gaussian, with Hartree-Fock (HF) and density functional theory (DFT)[3] methods, is used to optimise the structures of molecules and transition states (TS).

Optimisation of 1,5-hexadiene Conformers

Optimisation with HF/3-21G

Two anti- and one gauche- conformer of 1,5-hexadiene were optimised using the HF/3-21G method. They have been identified using the table in Appendix 1 from Dr. Mike Bearpark's 3rd Year Computational Chemistry Lab Module 3 course wiki.

Table 1: Optimisation of 1,5-hexadiene Conformers

Property	Anti1-Conformer	Anti2-Conformer	Gauche3-Conformer
Final Energy / a.u.	-231.69260	-231.69254	-231.69266
Final Energy / kJ mol-1	-608308.9	-608308.7	-608309.1
Point Group	C2	Ci	C1
Molecule	anti1	anti2	gauche3

In contrast to steric reasoning which dictate that the anti-conformers are more stable than the gauche-conformers due to steric repulsion between neighbouring carbon atoms in the gauche-conformer, the gauche3-conformer is the most stable conformer for 1,5-hexadiene.

This can be attributed to stereoelectronic reasons, particularly CH-π interaction. There exists favourable donation of electron density from the π_C=C orbital of the C=C double bond into the σ*_C-H orbital of the adjacent vinyl proton.

Optimisation of Anti2-Conformer with DFT/B3LYP/6-31G(d)

Comparison between HF/3-21G and DFT/B3LYP/6-31G(d) Optimisation

The HF/3-21G optimised anti2-conformer was further optimised with the DFT/B3LYP/6-31G(d) method to yield an improved structure with lower energy.

Table 2: Optimisation of Anti2-1,5-hexadiene

Properties	DFT/B3LYP/6-31G(d) Method	HF/3-21G Method
Final Energy / a.u.	-234.61170	-231.69254
Final Energy / kJ mol-1	-615973.0	-608308.7
C1-C4 dihedral angle / °	118.5	114.7

While there was little change in the bond lengths and bond angles between the DFT/B3LYP/6-31G(d) and HF/3-21G optimised structures, the dihedral angle between C1 and C4 increased significantly from 114.7° to 118.5°.

Comparison of Energies at 0K and 298K

The energy of anti2-1,5-hexadiene can be resolved into potential and kinetic energies, and from there the enthalphy and free energy of dissociation can be calculated. As these parameters are temperature-dependent, the computation was repeated at 0 K and 298.15 K to study the effect of temperature on the energies of anti2-1,5-hexadiene.

Table 3: Temperature-Dependence of Anti2-1,5-hexadiene Energies

Energies	At 0 K	At 298.15 K
Electronic Energy / a.u.	-234.55698	-234.61170
Sum of Electronic and Zero-point Energies) / a.u.	-234.46877	-234.46921
Sum of Electronic and Thermal Energies / a.u.	-234.46143	-234.46186
Sum of Electronic and Thermal Enthalpies / a.u.	-234.46049	-234.46091
Sum of Electronic and Thermal Free Energies / a.u.	-234.50037	-234.50082
Link	DOI:10042/to-2706	DOI:10042/to-2705

The total energy of the molecule becomes more negative as temperature increases. This is expected since the molecule absorbs more heat at higher temperatures, and thus thermal contribution to the energies increase.

Optimisation of Transition State Structures

Optimisation of Chair Transition State

Comparison of TS Optimisation Methods

The chair TS was optimised using HF/3-21G via two types of optimisation.

Opt 1: A direct TS(Berny) Optimisation

Opt 2: A ModRedundant Minimisation with frozen C-C lengths, at 2.20 Å, for the C atoms involved in bond breaking/forming; followed by a TS(Berny) Optimisation with Hessian Derivative calculation for the C-C bond breaking/forming lengths

The table below shows a comparison between the two techniques:

Table 4: Optimisation of Chair TS

Properties	Opt 1	Opt 2
Final Energy / a.u.	-234.61933	-231.61932
Final Energy / kJ mol-1	-615993.0	-608116.5
Imaginary Frequency / cm-1	-818	-818
C-C Bond Breaking/Forming Length / Å	2.02	2.02

As expected, both techniquess gave the same results for the energy of the TS. In addition, both techniques report the same C-C bond breaking/forming length, at 2.02 Å. They also give an imaginary frequency of -818 cm^-1, which upon animation of the vibration, shows asynchronous bond formation i.e. one bond breaks and the other forms simultaneously, as shown on the right. This is expected for the Cope Rearrangment, since it is an electrocyclic reaction.

In fact, the extra step of ModRedundant Minimisation in Opt 2 is unnecessary for this optimisation, since the guess structure for the chair TS is similar to the optimised TS.

However, for molecules in which the guess structure differs greatly from the true conformation, a direct TS(Berny) optimisation, as in Opt 1, cannot optimise the guess structure. This is observed later in the optimisation of the TS for the Diels-Alder reaction. In such situations, Opt 2 is applied. The ModRedundant Minimisation is used to first optimise the separate units of the TS individually, which the bond breaking/forming distance frozen. Upon completion, the coordinates are unfrozen, and the TS(Berny) optimisation can then be used to optimise the bond breaking/forming distance as part of the entire TS optimisation.

Intrinsic Reaction Coordinate

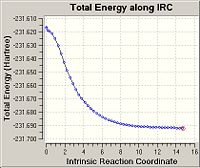
The Intrinsic Reaction Coordinate (IRC) calculation was conducted on the HF/3-21G optimised chair TS. The purpose of this calculation is to model the transformation from the chair TS down the potential energy surface to the final product of the reaction.

Initially, the IRC calculation was done with 50 points on the IRC pathway and computation of the force constants only once. The output showed no bond formation process, and hence it was deduced that the calculation was incomplete, as a 1,5-hexadiene structure was expected. Analysis of the IRC pathway also showed that the minimum on the potential energy surface has not been reached, as the points on the pathway do not reach an asymptote.

Th calculation was repeated with the same number of points on the IRC pathway, but this time with computation of force constants at every step. This allows the IRC calculation to determine if it is moving along the minimum energy pathway down the potential energy surface, and make changes to the pathway when necessary. This time, the process of bond forming to arrive at 1,5-hexadiene was observed in the output, and the IRC pathway also reached a plateau with minimum energy.

Table 2: Comparison of IRC Computations

Properties	Force Constant Computation Once	Force Constant Computation Always
Final Energy / a.u.	-231.68815	-231.69167
IRC Pathway
Structure	DOI:10042/to-2845	DOI:10042/to-2702

Analysis of the product in the successful IRC, with force constant calculation always on, showed that it is the gauche2-1,5-hexadiene conformer. The minimum energy reached in the IRC pathway, at -231.69167 a.u., also corresponds to the energy of the gauche2 conformer in Appendix 1 of Dr. Mike Bearpark's 3rd Year Computational Chemistry Lab Module 3 course wiki.

Optimisation of Boat Transition State

The boat TS was optimised via QST2 Optimisation, which requires the input of both the reagent and product molecules, and numbering of the atoms in the molecule to identify their positions in both reagent and product.

The following table shows the successful optimisation of the boat TS using QST2 Optimisation.

Table 5: Optimisation of Boat TS

Properties	QST2
Final Energy / a.u.	-231.60282
Final Energy / kJ mol-1	-608073.2
Imaginary Frequency / cm-1	-840
C-C Bond Breaking/Forming Length / Å	2.14

The presence of the imaginary frequency at -840 cm^-1 indicates that a TS was found. The movement of the bonds upon animation is shown in the diagram on the right. The vibration shows asynchronous bond formation ie. one bond is formed while the other is broken, as expected in the Cope Rearrangement.

The QST2 Optimisation is more tedious than the TS(Berny) optimisation utilised for the chair TS, as the exact geometry and numbering of the structures must be achieved for the optimisation to work. In practice, the QST2 optimisation failed to work even when the correct numbering and geometry was achieved; and the input had to be recreated before the calculation could succeed.

Hence, in further TS optimisations, the TS(Berny) Optimisation will be utilised over the QST2 method for its ease of usage.

Comparison of Chair and Boat Transition State

To obtain more accurate descriptions of both TS, the HF/3-21G optimised structures were sent for a final TS(Berny) optimisation and frequency calculation using the DFT/B3LYP/6-31G(d) method.

For the chair TS, all additional selections and keywords were retained, while for the boat TS, the additional keyword "Opt=CalcFC" had to be added. This allows the force constants to be calculated for the calculation to succeed.

A comparison of the structure and energies of the chair and boat TS, both at 0 K and 298.15 K, is made below.

Table 5: Comparison of Chair and Boat TS

Properties	Chair TS at 0 K	Chair TS at 298.15 K	Boat TS at 0 K	Boat TS at 295.15 K
Electronic Energy / a.u.	-234.55698	-234.55698	-234.54309	-234.54309
Sum of Electronic and Zero-Point Energies / a.u.	-234.41449	-234.41493	-234.40190	-234.40234
Sum of Electronic and Thermal Energies / a.u.	-234.40858	-234.40901	-234.39558	-234.39601
Sum of Electronic and Thermal Enthalpies / a.u.	-234.40763	-234.40807	-234.39464	-234.39506
Sum of Electronic and Thermal Free Energies / a.u.	-234.44336	-234.44382	-234.43130	-234.43175
Activation Energy / a.u.	0.05701	0.05655	0.10573	0.06862
Activation Energy / kJ mol-1	149.7	148.5	277.6	180.2
Imaginary Frequency / cm-1	-566	-566	-531	-531
C-C Bond Breaking/Forming Length / Å	1.97	1.97	2.21	2.21
TS Structure	chair	The jobs can be found at: DOI:10042/to-2874 for 0 K, and DOI:10042/to-2703 for 298.15 K	Tsboat	The jobs can be found at: DOI:10042/to-2704 for 0 K, and DOI:10042/to-2867 for 298.15 K

Note: The activation energies of the TS are measured with respect to anti2-1,3-hexadiene. Activation energy can be calculated by subtracting the electronic energy of anti2-1,3-hexadiene, at -234.50037 a.u., from that of the TS.

Comparing the results from the optimisation of the TS using DFT/B3LYP/6-31G(d) with those done with HF/6-31G, it is observed that the energies of both TS have decreased significantly, as have the imaginary frequencies. The C-C bond breaking/forming length has also changed.

This is because DFT/B3LYP/6-31G(d) is a higher level optimisation than HF/6-31G, and it adjusts the structure of TS, such as the C-C bond forming/breaking length, to further decrease its energy. The decrease in imaginary frequency indicates a gentler gradient of the potential energy curve at the maximum, indicating that this is a better optimisation.

From the table, it is observed that the chair TS is 0.01207 a.u., or 31.7 kJ mol^-1, more stable than the boat TS. This results in the chair TS having a lower activation energy of 148.5 kJ mol^-1 compared to the boat TS, at 180.2 kJ mol^-1 at room temperature. Hence, the chair TS is the expected TS for the Cope rearrangement of 1,5-hexadiene.

At 0 K, the activation energy of the chair TS is 149.7 kJ mol^-1, a relatively similar comparison to the experimental value of activation energy at 140±2 kJ mol^-1. However, the activation of the boat TS is much higher at 0 K as compared to room temperature, and at 277.6 kJ mol^-1, it significantly differs from the experimental value of 187±8 kJ mol^-1.

Diels-Alder Cycloaddition of Cis-Butadiene and Ethene

The Diels-Alder reaction is a cycloaddition reaction between a conjugated diene system and an alkene system to form a cyclohexene system. It is otherwise known as a [4+2] or п_4s+п_4s cycloaddition.

As with other cycloaddition reactions, the reaction occurs via a single cyclic, concerted transition state in which two σ bonds are formed between the termini of the two conjugated п systems.

Cis-butadiene and ethene react in the Diels-Alder reaction shown below.

In this and the next exercise, optimisation of the TS are done using Pople's Gaussian, first with the Semi-Empirical/AM1 method, followed by DFT/B3LYP/6-31G(d) method for a more accurate optimisation. Optimisation of the reagents are conducted directly with the DFT/B3LYP/6-31G(d) method as they are less computationally intensive.

Optimisation of Reagents

Optimisation of Cis-Butadiene

Energy of Cis-Butadiene

Table 5: Energy of Cis-Butadiene

Energy Type	Energy / a.u.
Electronic Energy	-155.98649
Sum of Electronic and Zero-Point Energies	-155.90114
Sum of Electronic and Thermal Energies	-155.89644
Sum of Electronic and Thermal Enthalpies	-155.89549
Sum of Electronic and Thermal Free Energies	-155.92785
Structure	cisbutadiene

Molecular Orbitals of Cis-Butadiene

The reactive molecular orbitals (MOs) of cis-butadiene are shown below, with their symmetries with respect to (wrt) the plane of symmetry (reflection) of the molecule indicated.

HOMO	LUMO
-0.34455 a.u.	0.01795 a.u.
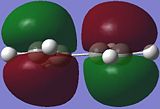
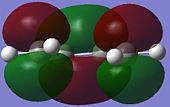
Anti-Symmetric (AS) wrt Plane	Symmetric (S) wrt Plane

The HOMO (highest occupied MO) of cis-butadiene is anti-symmetric (AS) with respect to the reflection plane of the molecule, as the phases are inverted.

Conversely, the LUMO (lowest occupied MO)is symmetric (S) with respect to the plane, since it can be reflected in the plane of symmetry of the molecule.

These assignments of orbital symmetry are important in pericyclic reactions, as they determine whether the reaction will proceed, and also the stereochemical outcome of the reaction.

Optimisation of Ethene

Energy of Ethene

Table 5: Energy of Ethene

Energy Type	Energy / a.u.
Electronic Energy	-78.58746
Sum of Electronic and Zero-Point Energies	-78.53623
Sum of Electronic and Thermal Energies	-78.53319
Sum of Electronic and Thermal Enthalpies	-78.53225
Sum of Electronic and Thermal Free Energies	-78.55776

Molecular Orbitals of Ethene

The reactive molecular orbitals (MOs) of ethene are shown below, with their symmetries with respect to (wrt) the plane of symmetry (reflection) of the molecule indicated.

HOMO	LUMO
-0.26664 a.u.	0.01881 a.u.
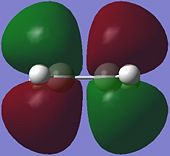
Symmetric (AS) wrt Plane	Anti-Symmetric (S) wrt Plane

The HOMO of ethene is symmetric (S) with respect to the plane of symmetry, while the LUMO is anti-symmetric (AS).

This is opposite to the symmetries of the HOMO and LUMO in cis-butadiene.

Thus, by the conservation of orbital symmetry, which states that only orbitals of the same symmetry can interact, orbital interaction between the HOMO of cis-butadiene and the LUMO of ethene, as well as between the LUMO of cis-butadiene and the HOMO of ethene, can occur.

Optimisation of TS

The optimisation of the TS was conducted in three consecutive steps:

1. Optimisation to a Minimum using Semi-empirical/AM1 method with ModRedundant to freeze the C-C bond forming distance at 2.1 Å
2. Optimisation to a TS(Berny)using Semi-empirical/AM1 method with ModRedundant to calculate the derivative of the C-C bond forming distance, which was unfrozen
3. Optimisation and Frequency calculation to a TS(Berny) using DFT/B3LYP/6-31G(d) method with the same techniques as in Step 2 but with additional keyword: Opt=NoEigen

The TS(Berny) optimisation techniques was chosen over the QST2 optimisation because of the strict requirements for QST2 optimisation, in which the position and numbering of the atoms in the reactants and products must be adhered to for the optimisation to proceed successfully.

Energy of TS

The following results were obtained from the Optimisation and Frequency TS(Berny) calculations using Semi-empirical/AM1 and DFT/B3LYP/6-31G(d).

Table 5: Energy of TS

Properties	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)
Electronic Energy / a.u.	0.121165	-234.54390
Sum of Electronic and Zero-Point Energies / a.u.	0.25328	-234.54390
Sum of Electronic and Thermal Energies / a.u.	0.25945	-234.54390
Sum of Electronic and Thermal Enthalpies / a.u.	0.26040	-234.54390
Sum of Electronic and Thermal Free Energies / a.u.	0.22402	-234.54390
Imaginary Frequency / cm-1	-956	-525
C-C Bond Forming Length / Å	2.12	2.27
Structure	DA1	DOI:10042/to-2701

In both optimisations, the presence of one imaginary frequency indicates that a TS has been found.

Comparing the results from the two optimisations, there is a vast difference in energies. However, there is no need for alarm at this difference since the semi-empirical and DFT methods report energies differently, and hence they cannot be compared. The increase in C-C bond forming length, however, can be attributed to the greater accuracy of the DFT/B3LYP/6-31G(d) optimisation. The increase in bond length results in a less steep potential energy slope to the TS maximum, as indicated by the decrease in imaginary frequency, and also resultign in a lower total energy of the TS.

Geometry of TS

The Jmol Applet on the right indicates the bond lengths and bond angles in the TS. Since the TS is symmetrical, only one of each pair of similar bonds/angles are shown. Also, the dihedral angle between C1 and C4 of cis-butadiene, which is 0.0°, is not shown. The bond breaking/forming length in the TS is 2.27 Å from the DFT/B3LYP/6-31G method. In contrast, the typical Csp3-Csp3 bond length is 1.53 Å, and the typical unconjugated Csp2-Csp2 bond length is 1.48 Å. However, the bond forming length is shorter than twice the van der Waals radius of the C atom, which is 1.70 Å for aliphatic carbons. This indicates that the C atoms are approaching within their van der Waals radii for bond formation, but the bond has not yet been fully formed, and so the distance between the atoms is still larger than that of a C-C single bond.

DA1

Molecular Orbitals of TS

The reactive molecular orbitals (MOs) of the TS are shown below, with their symmetries with respect to (wrt) the plane of symmetry (reflection) of the molecule indicated.

HOMO	LUMO
-0.32393 a.u.	0.02315 a.u.
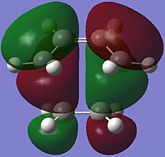
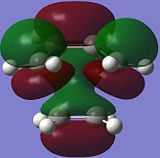
Anti-Symmetric (AS) wrt plane	Symmetric (S) wrt plane

By comparing the reactive molecular orbitals (MOs) of the TS with those of the reagents, it is observed that the HOMO of the TS is derived from the overlap of the HOMO of cis-butadiene and the LUMO of ethene. Meanwhile, the LUMO of the TS is built up of the LUMO of cis-butadiene and the HOMO of ethene.

This is consistent with the conservation of orbital symmetry, which states that the symmetry of the orbital formed form the overlap of two orbitals, must be the same as that of the initial orbitals. It also fits with MO theory since only filled orbitals can overlap with empty orbitals and vice versa.

Comparing the energies of the MOs of the reagents, it is also evident that the overlap of the HOMO of cis-butadiene and the LUMO of ethene will form a lower energy orbital than the overlap of the LUMO of cis-butadiene and the HOMO of ethene. This is observed in the HOMO and LUMO of the TS.

Activation Energy of Reaction

Summing the free energies of cis-butadiene and ethene, the total free energy of the reagents is -234.48561 a.u. In comparison, the free energy of the TS is -234.43289 a.u.

Hence, the activation energy, which is the difference in energy between the TS and the reagents, is 0.052720 a.u., or 138.4 kJ mol^-1.

This is supported by experimental data from literature which quotes the activation energy to be 115 ± 8 kJ mol^-1 at 0 K.

From TS to Product

Vibrational Frequencies

As discussed above, the imaginary vibrations of the TS indicate bond breaking/forming interactions in the TS, which either lead forward to the reagents or backward to the products.

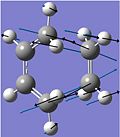
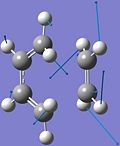
The frozen animation of the imaginary vibration of the TS is shown on the left. The blue arrows indicate the bond breaking interactions, which lead backward to the reagents, while the black arrows indicate the bond forming interactions, which lead forward to the products. The formation of the two bonds is synchronous, as expected for the concerted Diels-Alder reaction.

The lowest positive frequency vibration at 147 cm^-1 is a rock, shown on the right. In contrast to the imaginary vibration, the motion of the two termini of each unit of the TS is asynchronous ie. one end of the cis-butadiene and ethene termini move towards each other, while at the other end they move away from each other. Also, the magnitude of vibration is smaller than that of the imaginary vibration.

Intrinsic Reaction Coordinate

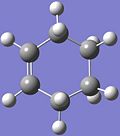
IRC was utilised to track the reaction from the TS down the potential energy surface via the minimum energy route to the product, cyclohexene, which is shown on the right. The IRC computation can also be found at {[DOI|10042/to-2881}}.

Conservation of Orbital Symmetry

By conservation of orbital symmetry, the transition of MOs from those in reagents to those in products via a concerted reaction must not change the symmetry of the orbitals. Reactions which follow these rule are symmetry-allowed, while those which do not are forbidden.

In the Diels-Alder reaction of cis-butadiene with ethene, orbital overlap between the anti-symmetric (AS) HOMO of cis-butadiene and the AS LUMO of ethene forms the HOMO of the cyclohexene product, which is also AS with respect to the plane of symmetry of the molecule. This retention of symmetry can also be observed in the HOMO of the TS.

Another rule in the conservation of orbital symmetry is that only orbitals of different symmetry can cross in energy. This rule is also applied since the LUMO of cis-butadiene, which is symmetric (S) with respect to the plane, overlaps with the S HOMO of ethene to form the LUMO of the TS and thus product, which retains the symmetry.

Energetically, the reaction is also allowed because the energy gap between the HOMO of cis-butadiene and the LUMO of ethene is small, and the product is more stable than the reagents. In addition, the small activation energy makes this reaction kinetically favourable as well.

Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

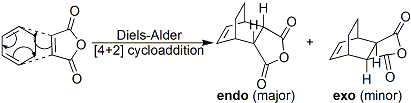
As with cis-butadiene and ethene, the reaction between cyclohexa-1,3-diene and maleic anhydride is also a Diels-Alder reaction. However, in contrast to the above reaction, two products are formed in this reaction, as shown below.

The endo and exo products are diastereomers, and their formation is dependent on the direction of attack of the diene (cyclohexa-1,3-diene) on the dienophile (maleic anhydride). As with most Diels-Alder reactions, the endo isomer is the major product of this reaction, which will be explained in the following exercise.

Optimisation of Reactants

Optimisation of Cyclo-1,3-hexadiene

Energy of Cyclo-1,3-hexadiene

Table 5: Energy of Cyclo-1,3-hexadiene

Energy Type	Energy / a.u.
Electronic Energy	-233.41892
Sum of Electronic and Zero-Point Energies	-233.29610
Sum of Electronic and Thermal Energies	-233.29092
Sum of Electronic and Thermal Enthalpies	-233.28998
Sum of Electronic and Thermal Free Energies	-233.32370
Structure	Cyclohexadiene

Molecular Orbitals of Cyclo-1,3-hexadiene

The reactive molecular orbitals (MOs) of cyclo-1,3-hexadiene are shown below, with their symmetries with respect to (wrt) the plane of symmetry (reflection) of the molecule indicated.

HOMO	LUMO
-0.01711 a.u.	-0.20551 a.u.
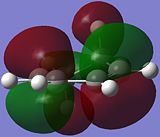
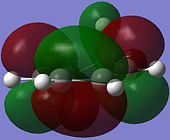
Anti-Symmetric (AS) wrt Plane	Symmetric (S) wrt Plane

The HOMO of cyclo-1,3-hexadiene is anti-symmetric (AS) with respect to the reflection plane of the molecule, while the LUMO is symmetric (S) with respect to the plane. This is similar to the symmetries of the HOMO and LUMO for cis-butadiene.

The DFT/B3LYP/6-31G(d) calculation shows the energy of the LUMO to be negative, when it is expected to be positive. However, this is a small negative energy and can be attributed to inadequacies in the method.

Optimisation of Maleic Anhydride

Energy of Maleic Anhydride

Table 5: Energy of Maleic Anhydride

Energy Type	Energy / a.u.
Electronic Energy	-379.28954
Sum of Electronic and Zero-Point Energies	-379.23366
Sum of Electronic and Thermal Energies	-379.22847
Sum of Electronic and Thermal Enthalpies	-379.22753
Sum of Electronic and Thermal Free Energies	-379.26273
Structure	cisbutadiene

Molecular Orbitals of Maleic Anhydride

The reactive molecular orbitals (MOs) of maleic anhydride are shown below, with their symmetries with respect to (wrt) the plane of symmetry (reflection) of the molecule indicated.

HOMO	LUMO
-0.11714 a.u.	-0.29929 a.u.
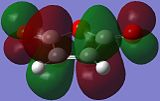
Anti-Symmetric (AS) wrt Plane	Anti-Symmetric (AS) wrt Plane

Both the HOMO and the LUMO of maleic anhydride are anti-symmetric (AS) with respect to the plane of symmetry (reflection) the molecule, as the phases are inverted.

Again, DFT/B3LYP/6-31G(d) calculation shows the energy of the LUMO to be negative, when it is expected to be positive.

Optimisation of TS

The optimisation of the TS was conducted in the same manner in the optimisation of the TS of the Diels-Alder reaction between cis-butadiene and ethene above, using the 3-step method.

Energies of TS

The following table shows the results for both the Semi-empirical/AM1 and DFT/B3LYP/6-31G(d) optimisations of the TS.

Table 5: Comparison of Endo and Exo TS

Properties	Endo TS with Semi-empirical/AM1	Endo TS with DFT/B3LYP/6-31G(d)	Exo TS with Semi-empirical/AM1	Exo TS with DFT/B3LYP/6-31G(d)
Electronic Energy / a.u.	-0.05151	-612.68340	-0.05042	-612.67931
Sum of Electronic and Zero-Point Energies / a.u.	0.13349	-612.50214	0.13488	-612.49801
Sum of Electronic and Thermal Energies / a.u.	0.14368	-612.49179	0.14488	-612.48766
Sum of Electronic and Thermal Enthalpies / a.u.	0.14463	-612.49084	0.14583	-612.48672
Sum of Electronic and Thermal Free Energies / a.u.	0.09735	-612.53833	0.09912	-612.53427
Imaginary Frequency / cm-1	-806	-447	-812	-448
C-C Bond Forming Length / Å	2.17	2.27	2.17	2.29
TS Structure	endo	DOI:10042/to-2700	exo	DOI:10042/to-2699

The presence of one imaginary frequency indicates that the optimised structure is indeed a TS.

Comparing the results from the two optimisations, there is a vast differnce in energies. However, there is no need for alarm at this difference since the semi-empirical and DFT methods report energies differently, and hence they cannot be compared. The increase in C-C bond forming length, however, can be attributed to the greater accuracy of the DFT/B3LYP/6-31G(d) optimisation. The increase in bond length results in a less steep potential energy slope to the TS maximum, as indicated by the decrease in imaginary frequency, and also resulting in a lower total energy of the TS.

From the table, it is observed that the endo TS is 0.00406 a.u., or 10.7 kJ mol^-1, more stable than the exo TS. The difference in energies of the endo and exo TS can be attributed to secondary orbital interactions in the endo TS which stabilises the structure, and will be discussed in the section on molecular orbitals.

This results in the endo TS having a lower activation energy to the exo TS as shown in the section on activation energies below. Hence, the endo TS is is predicted to give the kinetic product of the reaction.

Geometries of TS

A comparison of the bond lengths and bond angles of the endo and exo TS are made on the below.

The most evident difference between the two TS is that in the endo isomer, the H atoms on the maleic anhydride unit are pointing downward and the 5-membered ring is pointing upward; while in the exo isomer the H atoms on the maleic anhydride unit are pointing downward and the 5-membered ring is pointing upward.

Endo TS	Exo TS
endo	exo

There is little difference between the bond lengths and bond angles not involved in the C-C bond formation. Also, even the C-C bond forming length is similar for the TS, at 2.27 Å in the endo, and at 2.29 Å in the exo.

However, there is remarkable difference between bond angles and especially dihedral angles at the C-C bond forming site. The bond angle between the C=C double bond on the cyclo-1,3-hexadiene unit and the bond forming C on the maleic anhydride unit is 94.3° for the endo TS, and 99.1° in the exo. Also, the dihedral angle between the C=C double bond on the cyclo-1,3-hexadiene unit and the C-H bond on the maleic anhydride unit is 175.1° for the endo TS, and 70.6° in the exo.

Another difference which cannot be overlooked is the distance between the C of the carbonyl group in the maleic anhydride unit and the non-reacting C of the C=C double bond on theh cyclo-1,3-hexadiene unit nearest to it. In the endo TS, this distance is 2.99 Å, while in the exo TS it is 3.88 Å.

This distance is important for the secondary orbital overlap between the π*_C=O orbital from maleic anhydride and the π_C-C orbital from cyclo-1,3-hexadiene, which stabilises the TS. The shorter distance in the endo TS indicates that secondary orbital overlap can occur, while the longer distance in the exo TS spells the absence of this overlap.

Molecular Orbitals of TS

The reactive molecular orbitals (MOs) of both the endo and exo TS are shown below, with their symmetries with respect to (wrt) the plane of symmetry (reflection) of the molecule indicated.

Endo TS		Exo TS
HOMO (-0.24230 a.u.)	LUMO (-0.06771 a.u.)	HOMO (-0.07840 a.u.)	LUMO (-0.24215 a.u.)
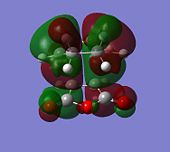
Anti-symmetric (AS) wrt plane	AS	AS	AS

Both the HOMO and the LUMO of the endoand exo TS are antisymmetric with respect to the plane of symmetry of the TS. Again, DFT/B3LYP/6-31G(d) calculation shows the energies of the LUMOs to be negative, when it is expected to be positive.

By comparing the reactive MOs of the TS with those of the reagents, it is observed that the HOMO of the TS is derived from the overlap of the HOMO of cyclo-1,3-hexadiene and the LUMO of maleic anhydride.

Activation Energy of Reaction

Summing the free energies of cyclo-1,3-hexadiene and maleic anhydride, the total free energy of the reagents is -612.58643 a.u.

This is utilised to calculate the activation energy for the endo and exo TS, as shown below.

Table 10: Activation Energies for TS

Activation Energy	Endo TS	Exo TS
Activation Energy / a.u.	0.04810	0.05216
Activation Energy / kJ mol-1	126.3	136.9

Note: The activation energies of the TS are measured with respect to the total free energy of the reagents. Activation energy can be calculated by subtracting the total free energy of the reagents, at -612.58643 a.u., from that of the TS.

From the table, it is observed that the activation energy for the endo TS is lower than that of the exo TS by 10.6 kJ mol^-1. Hence, the endo product is expected to be the kinetic product of the reaction.

From TS to Product

Vibrational Frequencies

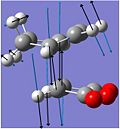
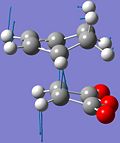
The imaginary vibrations of the TS indicate bond breaking/forming interactions in the TS, which either lead forward to the reagents or backward to the products.

The frozen animation of the imaginary vibration of the endo TS is shown on the left. The blue arrows indicate the bond breaking interactions, which lead backward to the reagents, while the black arrows indicate the bond forming interactions which form the products.

The frozen animation of the imaginary vibration of the exo TS is shown on the right, this time with the blue arrows indicating bond forming interactions to form the products.

In both the endo and the exo TS, the bond formation is synchronous ie. both bonds are formed concurrently, as expected for cycloadditions, which are concerted reactions.

Intrinsic Reaction Coordinate

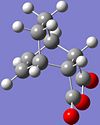
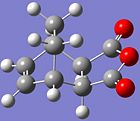
IRC was utilised to track the reaction from the Semi-empirical/AM1 optimised TS down the potential energy surface to the product for both the endo and exo TS.

The endo product is shown on the left, and can be found at DOI:10042/to-2847 . It can be identified by the H atoms on the 5-membered ring pointing upward, and the ring is pointing downward.

For the exo product, illustrated on the right, the H atoms on the 5-membered ring are pointing downward, and the ring is pointing upward. It can be found at DOI:10042/to-2879 .

Stereoselectivity in Diels-Alder Reactions

The selection of the endo product follows Alder's endo rule through the "maximum accumulation of unsaturated centers", which leads to a lower energy transition state and hence a more rapid reaction.

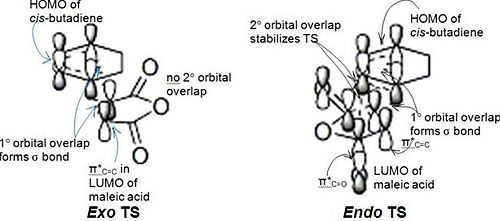
This selectivity is also explained by Woodward-Hoffmann rules and secondary orbital interactions for pericyclic reactions, as shown in the diagram below.

In both TS, the primary orbital overlap is the bonding interaction between the termini of the conjugated π system in the HOMO of cyclo-1,3-hexadiene and the π*_C=C of the LUMO in maleic anhydride. This results in the formation of two σ bonds between the terminis of the two π systems.

However, in the endo TS, there exists another favourable bonding interaction. This is between the center carbons of the conjugated π system in the HOMO of cyclo-1,3-hexadiene and the π*_C=O of the LUMO in maleic anhydride, thus stabilising the endo TS.

This secondary orbital interactions can also be observed in the MO picture of the HOMO on the right. In the cyclo-1,3-hexadiene subunit, the two C=C bonds are out-of-phase with each other as observed by the nodal plane between the two center carbons of the conjugated system. In the maleic anhydride subunit, there is a nodal plane between the carbon of the C=C and the carbon of the C=O groups. Another nodal plane exists between the C and O of the C=O bond on the maleic anhydride subunit, indicating a π*_C=O orbital. There is large overlap between the orbitals of the bond forming carbons, indicating a favourable bonding interaction.

There exists secondary orbital bonding interaction between the center carbon of the π conjugated system in the cyclo-1,3-hexadiene and the C atom of the π*_C=O orbital since their orbitals have the same phase. On closer inspection, it is observed that the shared electron density between these orbitals passes from the top face of the π conjugated system through the back of the molecule, through the bottom face of the maleic anhydride subunit to the orbital on the C atom of the π*_C=O orbital. This overlap stabilises the endo TS and thus lowers its activation energy.

In contrast, there is no such overlap observed in the exo TS, and thus the endo TS has a lower energy than the exo TS, so the kinetic product is expected to be the endo product.

As the Diels-Alder reaction is irreversible, the kinetic endo product dominates. Hence, it can be concluded that the cycloaddition of cyclohexa-1,3-diene and maleic anhydride is kinetically controlled.

Conclusion

This exercise has shown that the elucidation of transition states via the TS(Berny) optimisation method in Gaussian is useful in describing the mechanism of pericyclic reactions, which are kinetically controlled.

The energy of the transition states can explain the activation energy of a reaction, as well as predict the selectivity of the reaction by determining the kinetic product observed. In addition, molecular orbitals of the transition states can explain the selectivity of the reaction by determining orbital overlaps which are allowed.

One drawback of utilising Gaussian computations to study these pericyclic reactions is that it is only capable of computing the energies of the transition states and products to predict the kinetic and thermodynamic products. However, it is unable to predict whether the reaction is under kinetic or thermodynamic control, and thus it cannot determine the major product of the reaction. This can only be done experimentally.

In addition, computational studies of transition states may not always be capable of accurately predicting experimental observations for pericyclic reactions. Application of these methods to other known reactions must be investigated to determine its effectiveness. For example, the reactions investigated here are all thermal pericyclic reactions. The effectiveness of utilising Gaussian to study photoinduced pericyclic pathways was not investigated in this exercise, but a study by Gilch et al was successful in using quantum mechanical calculations in supporting experimental evidence. In addition, the computational study of high-pressure induced Diels-Alder reactions was also reported by Afarinkia et al.