Notes on accuracy and reported data

With the methods employed in this module:

Stated energies include an error of ±10 kJ/mol i.e.: ±0.004 Hartrees (to 1 s.f.). Consequently, all energies in atomic units are recorded to 3 decimal places.

Dipole moments are accurate to ~ 2 decimal places i.e.: ±0.01 D.

Frequencies in wavenumbers include a systematic error of 10%^[1]. By convention these are reported with no decimal places, and no scaling factors are employed in this report.

Infra-red intensities are likewise reported with no decimal places by convention, though the accuracy is much less than this.

Bond distances are accurate to ~±0.01 Å and are consequently recorded to 2 decimal places.

Bond angles are accurate to ~±0.1° and so are reported to 1 decimal place.

All stated errors are implicitly assumed hereon.

Investigating the PES of the Cope Rearrangement using Electronic Structure Methods

Fig 1.0: The Cope Rearrangement

The Cope rearrangement of 1,5-hexadiene is a [3,3]-sigmatropic pericyclic (concerted) reaction. Investigation of the potential energy surface (PES) from reactant to product has been the subject of many computational studies, the results finding their way into many high profile publications such as JACS.

Reactants and Products

The first part of this study is broken down into seven components and is concerned with exploring reactant and product conformations. Starting and ending structures were optimised to various local minima; energies and symmetries were compared. On one particular structure (close in energy to the global minimum), an optimisation was performed at a higher level theory/basis set and the vibrational frequencies were calculated and animated; thermochemical data was also extracted from the .log file.

a) This part requires the optimisation of a 1,5-hexadiene molecule with an “anti” linkage for the central carbons.

GV 5.0 was used to create the input file. The 1,5-hexadiene molecule was constructed using the controls palette, and the rotomer adjusted to using the “Modify Dihedral” tool (angle set to 180°). The structure was tidied using the “Clean” function.

The saved input file was opened in WordPad and the route section specified as per below (route section, title section and molecular specification displayed: note memory space increased to 500MB).

%mem=500MB
%chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope\1_input.chk
# opt hf/3-21g geom=connectivity

1st opt

0 1
 C                  0.27492503   -2.59749483    0.41886766
 H                 -0.47294531   -2.59024356    1.18407180
 C                  3.52743800   -4.53122317   -0.41897924
 H                  4.27530834   -4.53847444   -1.18418338
 C                  1.22527411   -3.80157593    0.28239298
 H                  1.37686809   -4.24701943    1.24338172
 H                  0.79473965   -4.52237333   -0.38092533
 C                  0.38582708   -1.54708750   -0.43019784
 H                 -0.27447895   -0.71048472   -0.33537312
 H                  1.13369624   -1.55433957   -1.19540312
 C                  3.41653595   -5.58163049    0.43008626
 H                  2.66866433   -5.57438009    1.19528915
 H                  4.07684353   -6.41823222    0.33526304
 C                  2.57708892   -3.32714207   -0.28250456
 H                  2.42549494   -2.88169856   -1.24349329
 H                  3.00762338   -2.60634466    0.38081375

 1 2 1.0 5 1.0 8 2.0
 2
 3 4 1.0 11 2.0 14 1.0
 4
 5 6 1.0 7 1.0 14 1.0
 6
 7
 8 9 1.0 10 1.0
 9
 10
 11 12 1.0 13 1.0
 12
 13
 14 15 1.0 16 1.0
 15
 16

The job was run using Gaussian 09w since computational expense is relatively low (considering the size of the molecule and the method/basis set combination) and therefore fits the laptop’s CPU specifications. On successful completion, the convergence of forces and displacements was immediately checked and found to be acceptable (values within stated thresholds).

Table 1.1 – Input and Output Geometries, app
Input	Output

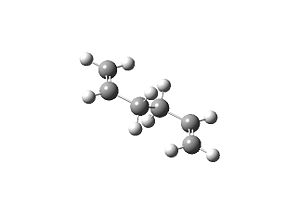Output: Media:csy07_cope_1.log

The energy of the molecule was found to be -231.689 a.u., it’s symmetry C_i{E,i}.

b) Similar to part a), this section requires the optimisation of a 1,5-hexadiene molecule with a “gauche” (synclinal) linkage for the central carbons. Based on steric considerations, the Newman projection suggests that the optimised molecule with be higher than that in part a).

GV 5.0 was used to create the molecule as before. The route section for the job is specified below and the job run on Gaussian 09w.

 %mem=500MB
 %chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope\2_input.chk
 # opt hf/3-21g geom=connectivity

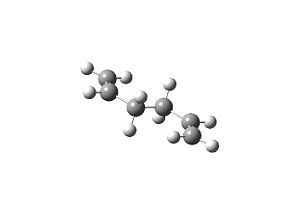
Table 1.2 – Input and Output Geometries, gauche
Input	Output

Output: Media:csy07_cope_2.log

The energy of the molecule was calculated as -231.688 a.u., higher than that for the app conformer as expected. The point group of the molecule is C₁.

c) Steric and stereoelectronic considerations must be made to predict the lowest energy conformer of 1,5-hexadiene. Three molecules were considered in this part: the first two were studied to identify the relative magnitude of various stereoelectronic contributions.

The largest orbital overlap occurs when the two vinyl moeities are parallel so that π component MOs mix. The first molecule was investigated to see how far the contribution of this stereoelectronic factor outweighed the steric strain implied in terms of energy.

First of all, two ethene molecules were optimised at the HF/3-21G level and run on Gaussian 9.0w (moeities treated separately from whole molecule to ensure that the effect being investigated was maximised).

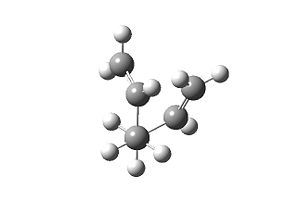
Table 1.3a – Input and Output Geometries, ethene moeities
Input	Output

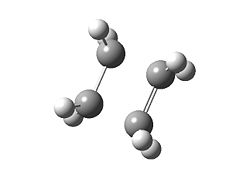Output: Media:csy07_cope_3a.log

The 1,5-hexadiene molecule was drawn on top of this structure, given that the new input geometry gives maximum π component MO overlap. This structure was optimised at the HF/3-21G level and run on Gaussian 9.0w.

Table 1.3b – Input and Output Geometries, 1,5-hexadiene
Input	Output

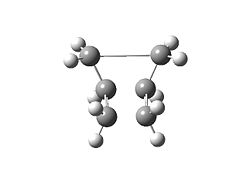Output: Media:csy07_cope_3b.log

The energy of the optimised structure is -231.674 a.u. Although this is higher than the lowest energy conformer found yet in part a), it’s interesting to note that the difference in energy at this level is only 0.015 a.u. (i.e. 40 kJ/mol). The favourable stereoelectronic interaction compensates to an extent the obvious angular strain in the final structure.

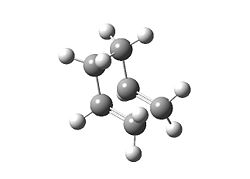
The second molecule was investigated to quantify the effect of π_C-C->π*_C-C interactions vs. steric strain. The starting geometry was drawn so that the vinyl fragments were in close proximity and at the correct, (near) planar orientation for orbital overlap. The molecule was optimised at the HF/3-21G level and run on Gaussian 9.0w.

Table 1.3c – Input and Output Geometries, 1,5-hexadiene
Input	Output

Output: Media:csy07_cope_3c.log

The energy of the optimised structure is -231.688 a.u. It is evident that the close proximity of the two vinyl hydrogen atoms forced a deviation away from π->π* contributions (i.e.: steric factors dominated in this case).

The last molecule sought to achieve a balance between steroelectronic and steric factors. 1,5-hexadiene was drawn in an app conformation for the central carbons (i.e.: minimising steric repulsion), and the terminal vinyl groups were rotated to make an angle of 90̊ with the C-H bond of the central carbons (i.e.: allowing σ_C-H->π*_C-C contributions). The structure was optimised at the HF/3-21G level and run on Gaussian 9.0w.

Table 1.3d – Input and Output Geometries, 1,5-hexadiene
Input	Output

Output: Media:csy07_cope_3d.log

The energy of this conformer was calculated as -231.693 a.u., the lowest energy conformer yet.

d) Viewing the .jpg files and comparing the energies to 5 d.p., it is evident that the lowest energy molecule found in part c) corresponds to molecule anti2 in Appendix 1.

e) The anti2 conformer was studied in part c), the .log file confirms it has C_i symmetry.

f)The .chk of the anti2 geometry optimised at the HF/3-21G level was opened in GV 5.0; a new input file was saved and the route section was detailed in WordPad:

 
 %chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope\app2_631Gd.chk
 # opt b3lyp/6-31g(d) geom=connectivity

Gaussian 9.0w was used to perform the calculation.

Table 1.6a – Input and Output Geometries, anti2
Input	Output

Output: Media:csy07_cope_4.log

The energy of the molecule at the B3LYP/6-31G(d) level of theory is -234.612 a.u. contrasted to a value of -231.693 a.u. at the HF/3-21G level i.e.: a decrease in calculation value of 2.919 a.u. or 7663.84 kJ/mol.

Visually there is little difference between the input and output geometries: geometric parameters are summarised in table 1.6b.

Table 1.6b – Summary of Geometric Parameters, anti2 conformer
Parameter	Input	Output
C1-C2 bond length / Å	1.31	1.33
C2-C3 bond length / Å	1.51	1.50
C3-C4 bond length / Å	1.55	1.55
C4-C5 bond length / Å	1.51	1.50
C5-C6 bond length / Å	1.32	1.33
C1-C2-C3-C4 dihedral angle / ̊	-114.6	-118.6
C2-C3-C4-C5 dihedral angle / ̊	-180.0	-180.0
C3-C4-C5-C6 dihedral angle / ̊	114.7	118.6

g) The .chk of the anti2 geometry optimised at the B3LYP/6-31G(d) level was opened in GV 5.0; a new input file was saved and the route section was detailed in WordPad:

 
%chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope\app2_freq.chk
# freq b3lyp/6-31g(d) geom=connectivity

Gaussian 9.0w was used to perform the calculation.

Output: Media:csy07_cope_5.log

low

high

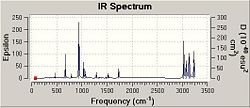The IR spectrum for the geometry optimised at this level is shown. No negative frequencies are found: the lowest (74 cm^-1) and highest (3234 cm^-1) energy vibrations are animated. The frequency analysis essentially takes the second derivative of the PES surface i.e.: -d²E(R)/dR². Given that the optimised geometry is at a stationary point, the frequency analysis determines whether this is a minimum or a maximum. In the case of 1,5-hexadiene, there are too many nuclear position variables to imagine the PES in 3D space (as is often the case). But fixing all but 2 nuclear position variables allows us to imagine the PES in 3D space. Although a minimum may be found on this particular surface (i.e.: Gaussian 09w may "think" it has found a stationary point during an optimisation), when the variables which were fixed are allowed to change again that point may no longer be a minimum. The frequency calculation performed shows that in this case, the optimised geometry is at a minimum point on the PES on consideration of all variables.

The following thermochemical data were extracted from the .log file:

 Sum of electronic and zero-point Energies=           -234.469204
 Sum of electronic and thermal Energies=              -234.461857
 Sum of electronic and thermal Enthalpies=            -234.460913
 Sum of electronic and thermal Free Energies=         -234.500777

Optimising the “Chair” and “Boat” Transition Structures

This part is concerned with finding the intermediate geometries (i.e.: the transition state structures) of the Cope rearrangement corresponding to the “chair” and “boat” configurations.

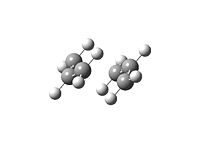a) In this part an allyl fragment was optimised at the HF/3-21G level of theory. The fragment was used as a skeleton for the input geometry of the “chair” TS structures in GV 5.0: the terminal distance between the allyl ends was set to 2.2 Å. The input geometry is displayed.

This input geometry was optimised to the “chair” TS by 2 methods: first, by computing the force constant matrix, and second, by using the frozen coordinate method. These will be explored in the next stages.

b) The input geometry from part a) was used as a starting point for the optimisation. The route section for the job was specified below:

%chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope b\b.chk
# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity

The geometry obtained is shown below, along with the imaginary frequency found at -818 cm^-1 which corresponds to the Cope rearrangement.

Optimised Geometry

Imaginary frequency

high

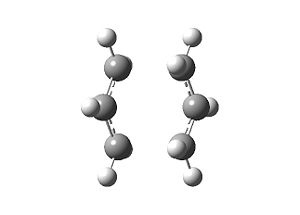Output: Media:csy07_copeb_1.log

c)The optimised structure from part a) is now used to find the TS via the frozen coordinate method. The input file for this job is specified below:

 %chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope b\c.chk
# opt=modredundant hf/3-21g geom=connectivity

Title Card Required

0 1

…

B 3 13 F
B 5 11 F

“B 3 13 F” and “B 5 11 F” mean that the Bond between atoms 3 and 13 and the Bond between atoms 5 and 11 (i.e.: the terminal carbons) have been Frozen at the stated geometry (length set to 2.2 Å).

The optimised geometry is similar to that obtained in part b except that the distance between the terminal carbons is set at 2.2 Å.

Output: Media:csy07_copeb_2.log

d)The geometry from the .chk file at the end of part c) was used as input for this stage. The aim here was to fully optimise the molecule by unfreezing the bond lengths. The input file is specified below:

%mem=500MB
%chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope b\d.chk
# opt=(ts,modredundant,noeigen) freq hf/3-21g geom=connectivity

Title Card Required

0 1

…

B 11 5 D
B 13 3 D

Output: Media:csy07_copeb_3.log

The parameters from the results summary of both methods are summarised below.

Table 2.4 – Parameter comparison between the Force Constant Method (FCM) and the Redundant Coordinate Method (RCM)
Forming C-C bond length / Å	2.02	2.02
Existing C-C bond length / Å	1.39	1.39
<C-C-C / ̊	120.5	120.5
Energy / a.u.	-231.62	-231.69
RMS Gradient / a.u.	0.000017	0.000029
Dipole / D	0.0001	0.0001
Symmetry	C_2h	C_2h
Imaginary Vibration / cm^-1	-818.0	-817.8

e)The optimised reactant from the previous part (i.e. the anti2 conformer) was pasted into GV 5.0 and labelled. The product, being symmetric to the reactant, was also based on the geometry of the anti2 conformer and labelled to match the scheme of the reactant.

These were specifed to set up a QST2 calculation. The route section is displayed below:

 %chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope b\qst2_1.chk
# opt=(calcfc,qst2,noeigen) freq hf/3-21g geom=connectivity

Output: Media:csy07_copeb_4.log

This job fails; the geometry obtained is displayed. The calculation only translated the top allyl fragment: no rotation or further manipulation was considered. The failure of the job indicated that to locate the boat TS structure, the starting and ending geometries had to be changed.

Input

Output

Imaginary frequency at -818 cm^-1

low

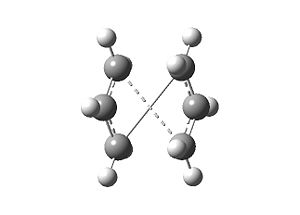To get the job to complete successfully, the reactant and product geometries were manipulated to look more like the boat TS. After specifying exactly the same QST2 job as before, the boat TS was found.

Input

Output

Imaginary frequency at -840 cm^-1

low

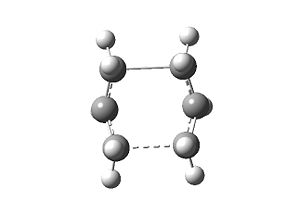Output: Media:csy07_copeb_5.log

f) To predict the conformers linked by the chair and the boat TS the Intrinsic Reaction Coordinate (IRC) method was employed. The Cope rearrangment is symmterical so the reaction coordinate was calculated only in the forward direction.

The .chk file from part b) was used as input here. The route section for the IRC calculation is detailed below:

 %chk=C:\Documents and Settings\csy07\Desktop\mod 3\cope b\IRC_fromb.chk
# irc=(forward,maxpoints=50,calcfc,maxcycle=50) rhf/3-21g geom=connectivity

Maxpoints and maxcycle were set to 50 so that the calculation didn’t end prematurely (effectively employing method ii) here).

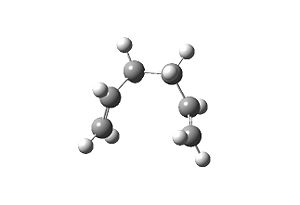
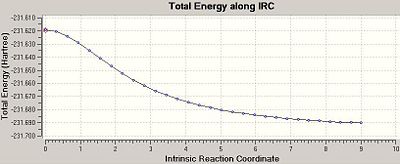
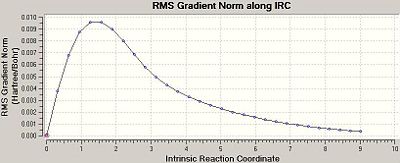
The chair TS and the product ending geometry is displayed below, along with a plot of the IRC calculation’s progress. Evidently the product is not listed in Appendix 1 (the energy of the product is recorded as -231.690008863 a.u.), but the conformation is close to that of gauche 2.

Input	Output

Output: Media:csy07_copeb_6.log

g) Using the geometries optimised at the HF/3-21G level, the chair and boat TS structures were optimised again at the higher B3LYP/6-31G* level. After creating the input files the route section of each was specified as per below:

 %chk=/work/csy07/Mod3/b3lyp_chair.chk
# opt=(calcfc,ts,noeigen) freq b3lyp/6-31g(d) geom=connectivity

The calculations optimised successfully. The following results were obtained and compared to the results from the HF/3-21G level and to experiment.

Output: Media:csy07_copeb_chair.log

Output: Media:csy07_copeb_boat.log

Table 3.7 Chair and Boat TS parameters
	HF/3-21G			B3LYP/6-31G*
	Electronic Energy / a.u.	Sum of Electronic and Zero-Point Energies / a.u.	Sum of Electronic and Thermal Energies / a.u.	Electronic Energy / a.u.	Sum of Electronic and Zero-Point Energies / a.u.	Sum of Electronic and Thermal Energies / a.u.
		At 0 K	At 298.15 K		At 0 K	At 298.15 K
Chair TS	-231.62	-231.47	-231.46	-234.55	-234.41	-234.41
Boat TS	-231.60	-231.45	-231.45	-234.54	-234.40	-234.40
Anti 2 conformer	-231.69	-231.54	-231.53	-234.61	-234.47	-234.46

	Table 3.8 Activation Enthalpies
	HF/3-21G / kcal/mol	HF/3-21G / kcal/mol	*B3LYP/6-31G / kcal/mol**	*B3LYP/6-31G / kcal/mol**	Expt. Value / kcal/mol
	At 0 K	At 298.15 K	At 0 K	At 298.15 K	At 0 K
(ΔE (Chair)	45.54	44.77	32.65	33.21	33.5 ± 0.5
ΔE (Boat)	55.62	54.66	41.88	41.34	44.7 ± 2.0

Evidently the chair TS is the one of lower energy and the transition state through which the Cope rearrangement proceeds.

The Diels-Alder cycloaddition

The Diels-Alder reactions form perhaps the most famous class of cycloadditions. Orbital symmetry dictates whether or not a reaction between π components may occur: the HOMO and the LUMO levels of reactants must have the same symmetry so that electron density overlap may occur.

For the first 2 parts of this section the [4s+2s]cycloaddition reaction between cis-butadiene and ethene is investigated (orbital symmetry found, transition state studied). For the last part, the stereochemistry of the DA reaction between maleic anhydride and cyclohexa-1,3-diene is studied.

Part 1

Cis-butadiene and ethene were drawn in GV 5.0 and optimised at the AM1 semi-empirical method. For cis-butadiene the geometries from the .chk files were used as inputs for a second optimisation at the higher B3LYP/3-21G level. The HOMO and LUMO of both components were plotted at the two levels of theory and the orbital symmetry with respect to the plane here was determined.

Table 3.1 – HOMOs and LUMOs of each π component with symmetry
Component	HOMO (AM1)	HOMO(B3LYP/3-21G)	Symmetry wrt plane	LUMO (AM1)	LUMO(B3LYP/3-21G)	Symmetry wrt plane
Cis-butadiene			a			s
Ethene		No calculation	s		No calculation	a

Output: Media:csy07_DA_AM1.log

Output: Media:csy07_DA_B3LYP.log

In terms of symmetry, the HOMO of each component can interact with the LUMO of the other.

Part 2

To optimise to the transition state, an structure was drawn which is envelope-type in geometry (i.e.: close to the TS) in GV 5.0. The route section for the file is specified below:

%chk=/work/csy07/Mod3/DA_2.chk
 # opt=(calcfc,ts,noeigen) freq am1 geom=connectivity pop=full

The jobs were run on the HPC:CX1 service rather than SCAN. This was done essentially to save queuing time, and also to use one of the latest development version of Gaussian (gdvh01_725). The template code for the jobscript.sh is given below:

#PBS -l ncpus=1
#PBS -l mem=1200mb
#PBS -l walltime=3:00:00
#PBS -j oe

export FLD=Mod3
export FLNM=DA_2

module load gaussian/devel-modules
module load gdvh01_725

echo $FLNM.com

gdv < $HOME/$FLD/$FLNM.com > $WORK/$FLD/$FLNM.log

After the job completed, the optimised geometry was exported as a .fchk file and used as input for a higher level calculation:

%chk=/work/csy07/Mod3/DA_2_b.chk
# opt=(calcfc,ts,noeigen) freq b3lyp/3-21g geom=connectivity pop=full

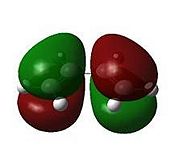
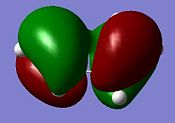
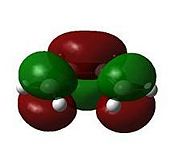
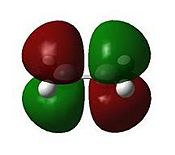
The transition state geometry is shown below along with the HOMO and LUMO with symmetry and the imaginary frequency at -956 cm^-1.

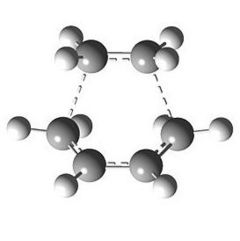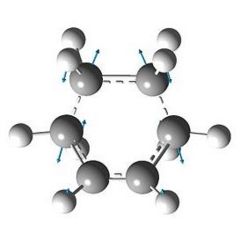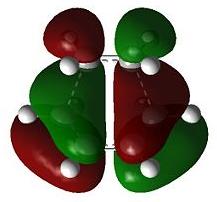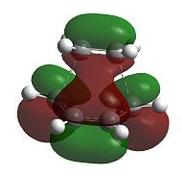The two new σ bonds are each 2.12 Å long in the TS, compared to a sp² bond length of 1.32 Å and a sp³ bond length of 1.54 Å. The van der Waals radius of the C atom is 1.70 Å^[2]. This indicates that the new C-C bonds in the TS are not yet covalent in nature, but are rather the result of van der Waals interactions. The frequency analysis shows a negative frequency at -956 cm^-1, the vibration corresponding to the reaction path and shows the formation of the two is synchronous (i.e.: concerted). By way of contrast, the lowest positive frequency at 147 cm^-1 shows σ bond formation as asynchronous. The TS HOMO has symmtery “a” to the plane whilst the LUMO has symmtery “s” to the plane. The LUMO of ethene and the HOMO of cis-butadiene have been used to form the HOMO of the TS. Since the interacting MOs of each component have the same symmetry (“a”) the reaction is allowed.

Part 3

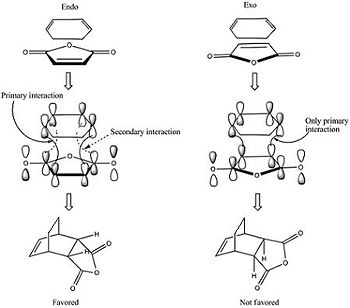Fig 3.3a: Cycloaddition reaction of cyclohexa-1,3-diene with maleic anhydride ^[3]

The reaction of cyclohexa-1,3-diene with maleic anhydride is depicted. Two products are possible: the endo- (kinetically favoured) form or the exo- (kinetically disfavoured) form. Structures close to the TS were drawn for each isomer and the route section for each file specified below:

 %chk=F:\y3 comp labs\mod 3\DA\DA_3endo_b.chk
# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity pop=full

The .chk for these files were opened in GV 5.0 and the geometry used as input for a second optimisation at the B3LYP/3-21G level:

%chk=/work/csy07/Mod3/DA_3endo_c.chk
# opt=(calcfc,ts,noeigen) freq b3lyp/3-21g geom=connectivity pop=full

These jobs were run on HPC:CX1. The output geometries are displayed below along with the HOMO of each:

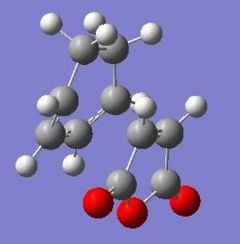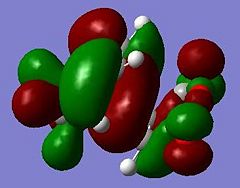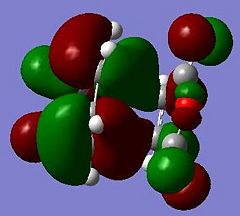Output: Media:csy07_DA_AM1_endo.log

Output: Media:csy07_DA_B3LYP_endo.log

Output: Media:csy07_DA_AM1_exo.log

Output: Media:csy07_DA_B3LYP_exo.log

The .log files from the B3LYP/3-21G calculations identify the endo TS energy as -609.3209959 a.u. and the exo TS energy as -609.3165213 a.u.. In other words, the exo TS in higher in energy than the endo TS by 0.0044746 a.u. or 10 kJ/mol (as expected since the endo product is the kinetic product).

Considering the geometry of the exo TS, the steric repulsion between the anhydride group and the cyclohexadiene ring (the anhydride group being directly over the cyclohexadiene ring) may account for the higher energy. Explicitly, in the exo TS there exist steric repulsions between the C=O moieties of the maleic anhydride ring and the C-H bridge bonds. The interaction is much less severe in the endo TS.

The two σ bonds being formed in both TS structures are each 1.39Å long, compared to a sp² bond length of 1.32 Å and a sp³ bond length of 1.54 Å. The double bond of maleic anhydride is 1.41Å long: longer than a normal sp² bond length indicating that this bond is breaking to an sp³ single bond. Similarly the single bond of cyclohexadiene is shorter than 1.54 Å since these carbons are becoming sp² hybridised.

The HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride are used to form the HOMO of both TS structures.

Looking at the HOMO between the -(C=O)-O-(C=O)- fragment and the remainder of the system, it is evident that the endo- TS structure is more stable than the exo- TS structure for stereoelectronic as well as steric reasons (discussed above). The C=C π orbital of the cyclohexadiene fragment can overlap with the π* orbital of the -(C=O)-O-(C=O)- fragment; the two MOs mix to form a lower energy level. The symmetry of the component MOs allows this to happen, and this only occurs in the endo- TS due to the relative geometry of the structure bringing the two fragments closer together. This orbital interaction , aka the secondary orbital overlap effect, is illustrated in Fig 3.3a.

↑ M.W. Wong, Chem Phys Lett (1996), 256: 391.
↑ Chemical Rubber Company Handbook of Chemistry and Physics, 59th Edition, CRC Press, Inc, 1979
↑ http://images.google.co.uk/imgres?imgurl=http://upload.wikimedia.org/wikipedia/commons/c/cd/Cyclopentadiene_Maleic_Anhydride_Diels_Alder.png&imgrefurl=http://commons.wikimedia.org/wiki/File:Cyclopentadiene_Maleic_Anhydride_Diels_Alder.png&usg=__tTTxbtuyO2JGQmkycl03soOxQl0=&h=395&w=449&sz=44&hl=en&start=1&sig2=eHYX00Ch8SuEaKHDMQnbZg&um=1&itbs=1&tbnid=PHEG_sH0HrDkyM:&tbnh=112&tbnw=127&prev=/images%3Fq%3Ddiels%2Balder%2Bmaleic%2Banhydride%26um%3D1%26hl%3Den%26client%3Dfirefox-a%26hs%3DKSY%26sa%3DG%26rls%3Dorg.mozilla:en-GB:official%26tbs%3Disch:1&ei=lEmBS6bJINuX4gafw-jsBg

[1] M.W. Wong, Chem Phys Lett (1996), 256: 391.

[2] Chemical Rubber Company Handbook of Chemistry and Physics, 59th Edition, CRC Press, Inc, 1979

[3] ttp://images.google.co.uk/imgres?imgurl=http://upload.wikimedia.org/wikipedia/commons/c/cd/Cyclopentadiene_Maleic_Anhydride_Diels_Alder.png&imgrefurl=http://commons.wikimedia.org/wiki/File:Cyclopentadiene_Maleic_Anhydride_Diels_Alder.png&usg=__tTTxbtuyO2JGQmkycl03soOxQl0=&h=395&w=449&sz=44&hl=en&start=1&sig2=eHYX00Ch8SuEaKHDMQnbZg&um=1&itbs=1&tbnid=PHEG_sH0HrDkyM:&tbnh=112&tbnw=127&prev=/images%3Fq%3Ddiels%2Balder%2Bmaleic%2Banhydride%26um%3D1%26hl%3Den%26client%3Dfirefox-a%26hs%3DKSY%26sa%3DG%26rls%3Dorg.mozilla:en-GB:official%26tbs%3Disch:1&ei=lEmBS6bJINuX4gafw-jsBg

[1]

[2]

[3]