Module 3 - Transition States

Cope Rearrangement

Optimisation of the Reactants

In this section the aim is to investigate the transition states of the cope rearrangement, which is a 3,3-sigmatropic rearrangement in 1,5-dienes. Specifically, 1,5-hexadiene, whose transition state proceeds via either a chair or boat conformation for the transition state (Figure 1). It is generally accepted that the chair transition state is the lower energy pathway. Using various computational methods these transition states will be investigated to find optimised energy minima.

1,5-hexadiene was drawn in GuassView in an anti-periplanar arrangement. Once drawn, the molecule was optimised using a hartree-fock method, and a 3-21G basis set. The molecule was redrawn in a different anti conformer and optimised, this process was repeated until all of the anti conformers had been optimised and the data recorded in Table 1.1. The same was done for three of the gauche conformers.

**Table 1.1**
	Conformers of 1,5-hexadiene
molecule	structure	point group	energy
XML error: Mismatched tag at line 7		C₁	-231.69266121
XML error: Mismatched tag at line 7		C₂	-231.69153
XML error: Mismatched tag at line 7		C₂	-231.68771617
XML error: Mismatched tag at line 7		C₁	-231.69260235
XML error: Mismatched tag at line 7		C_i	-231.69253526
XML error: Mismatched tag at line 7		C_2h	-231.68907065
XML error: Mismatched tag at line 7		C₁	-231.69097052

From Table 1.1 it is clear that the lowest energy conformer is gauche 3, which is contrary to the expectation of anti conformers being more stable due to reduced steric repulsion. Admittedly, anti conformers are seen to be lower than gauche ones but the low energy gauche 3 conformer can be explained by a stabilising donation of electron density from the C=C π orbital into the C-H σ* orbital.

The anti 2 conformer was reoptimised - this time using a DFT method (B3LYP, with a 6-31G basis set). Whilst, it is not completely reasonable to compare the resulting energies from these two different energies on grounds that different techniques were used, it is possible to see that the DFT method tweaked some of the bond lengths and dihedral angles to produce a far lower energy conformer. This can be seen in Table 1.2.

**Table 1.2**
	A Comparison of Techniques Anti 2 - HF vs DFT
method	energy	point group	central dihedral angle/^o	C=C bond length/Å	H₂C-CH₂ bond length/Å
XML error: Mismatched tag at line 7	-231.69253526	C_i	180.0	1.316	1.553
XML error: Mismatched tag at line 7	-234.55970439	C_i	180.0	1.34	1.555

The results of the two different methods used appear very similar. The structures seem to be visually identically from their .mol files. However, on closer inspection of the measurements there are a few subtle differences between the structures. The bond lengths are marginally longer when using the DFT method compared to the HF method and the angles aer very consistent. In general the results agree well with the literature.

Frequency Analysis

Using the DFT optimised structure, which had already been subjected to frequency analysis the frequency data was examined. This was done so that it could be confirmed that a minimum had indeed been reached. All vibrational frequencies were found to be positive, showing that this was the case (Table 1.3).

**Table 1.3**
	Frequency data of DFT optimised Anti 2 structure
frequency/cm^-1	intensity	vibration	description
1728	19		Asymmetric C=C stretch
3028	59		C-H stretch
3081	36		C-H stretch
3140	60		C-H stretch
3159	14		alkene C-H stretch
3244	56		alkene C-H stretch

From within the .log file it was possible to draw some interesting thermochemistry data (Table 1.4). This data was collected at 298K, but if there had been more time available it would have been interesting to compare this data with a range of temperatures, specifically absolute zero.

**Table 1.4**
	Frequency data of DFT optimised Anti 2 structure
Property	Symbols for Energies	Energy/a.u
Sum of electronic and zero-point Energies	E(0 K) = E_elec + ZPE	-234.4162
Sum of electronic and thermal Energies	E(298.15 K) = E(0 K) + E_vib + E_rot + E_trans	-234.4090
Sum of electronic and thermal Enthalpies	H = E (298.15K) + RT	-234.4080
Sum of electronic and thermal Free Energies	G = H - TS	-234.4478

The next stage was to investigate the chair transition state with C_2h symmetry and the boat transition state, which had C_2v symmetry.

Chair Transition State

Initially, a CH2CHCH2 fragment was drawn in GaussView, which was subsequently optimised using an Hartree-Fock method and a 3-21G basis set. This optimised fragment was then copied and positioned into a chair conformation whose terminal carbon atoms separated by a distance of 2.2Å. This newly created chair transition state was then optimised using two different methods.

Firstly, a Berny TS method was performed, in which a force constant matrix was calculated and subsequently recalculated throughout the optimisation. It was imperative that the initial estimate for this matix was accurate owing to the sensitivity of the method to input geometry. If a poor intial guess was made then the potential energy surface calculated would differ from the correct one. Secondly, a Frozen Coordinate method was performed, in which the reaction coordinate was frozen and the rest of the molecule was optimised. The molecule was then unfrozen and the transition state reoptimised again.

Berny TS Method

The calculation was set up for opt+freq to optimise to a TS(Berny) and to calculate force constants once. The additional keywords “opt=noeigen” were also added to prevent the calculation from crashing if more than one imaginary frequency was found.

The results were obtained (Table 1.5). They showed that the optimised transition state had a terminal C-C bond length of 2.02Å. The transition state was confirmed since there was an imaginary vibrational frequency at 817.85cm^-1, which agreed well with the expected value. This vibration can be interpreted as the Cope rearrangement, and specifically the formation/breaking of the relevant bonds. The vibration is asymmetrical since one bond is formed as the other is broken, which can be interpreted the process is a pericyclic reaction.

This vibration can be seen below and is the same as reported in the literature (Figure 2).

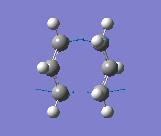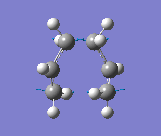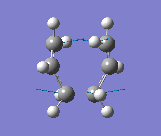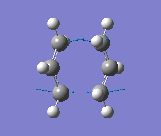
*Figure 2 - Berny TS imaginary vibration*

Frozen Coordinate Method

The two allyl fragments that had been drawn in the same gaussview window were optimised with a fixed distance between the terminal carbons of 2.2Å. To do this the reaction coordinates were frozen and the rest of the molecule was optimised around it. This frozen distance was then defrosted and the molecule was reoptimised. One of the advantages of this method compared with using a force constant calculation is that in the frozen coordinate approach the entire hessian need not be computed, merely differentiated along the reaction coordinate. The results obtained by this method agree well with BERNY TS method (Table 1.5). Despite the results being consistent, having arguably reached the same optimisation point, there are problems with each technique: the frozen coordinate method relies on a good estimate for the terminal dinstance between allyl fragments; the Berny TS relies upon an accurate initial structure and also takes up more time and computational power.

**Table 1.5**
	Optimised Through a TS (Berny)	Optimised Through a Frozen Coordinate Method
Optimised TS Structure
Terminal C-C bond length/Å	2.02	2.02
Energy/a.u	-231.6193	-231.6193
Imaginary Frequency/cm^-1	-818	-818

Boat Transition State

QST2 method

The boat transition state was optimised using a QST2 method. This method relies on reactants and products being specified for a given reaction and then the transition state being calculated. The previously optimised “anti 2" structure was opened in GaussView as both the reactant and product. The atoms were labelled such that they corresponded to the relevant reaction. It should be noted that on the first attempt of calculating the transition state using the QST2 method the experiment failed. This was because the reactants didn't resemble the boat transition state enough and so the reaction failed. The geometry of the reactant and product molecules was thus altered. the central dihedral angle was changed to 0^o and the two CH2CH2CH bond angles were changed to 100^o (Figure 3). The job was resubmitted and the results can be seen in Table 1.6.

**Table 1.6**
	Optimised Through a QST2 method
Vibration
Energy/a.u	-231.6028
Imaginary Frequency/cm^-1	-840
Intensity	2
Terminal C-C bond length/Å	2.14

The vibrational frequency present at -840 cm^-1 shows that a transition state has been found. Despite the value being more negative for the boat transition state than that of the chair it still shows the same vibration that can be attributed to the breaking and formation of bonds between terminal carbon atoms. A look at both vibrations show that they the same. The terminal carbon distance is longer in the boat transition state than the chair. This is supported by the energies of the transition states since the chair has a slightly lower energy than that of the boat.

The problem with the QTS2 method is that it is very time consuming and requires more diligence than the Berny TS method. Poor numbering resulted in the calculation failing several times and so the Berny TS method is preferred.

*Figure 3 - Altered Cope reactant and product*

Intrinsic Reaction Coordinate Method

The advantage of the intrinsic reaction coordinate method is that it allows a plot of the minimum energy path from a transition state down to its local minimum on a potential energy surface. Initially the calculations for the chair transition state, from the frozen coordinate method optimisation, were computed with 50 steps. Unfortunately, it was seen that the structure had reached a minimum after this and only 45 points had been calculated, which was confirmed by the RMS plot (Table 1.7). The force constants were thus calculated for every step, which did find a minimum whose energy corresponded well to the literature. Other methods could have been performed to obtain a minimum geometry: try a minimisation on the last point of the IRC or reperform the IRC with a larger number of points until a minimum is reached. The method chosen is the best but the most demanding computationally. The method of minimisation of the last point of the IRC is the worst as it can lead to the wrong structure but it is the fastest to run.

The results of the first, failed, IRC method in Table 1.7. The final structure obtained is clearly almost there but is not quite a minimum, as shown by the RMS gradient plot. This was why another IRC was run using the same starting structure but force constants were claculated at every step, which was a very time consuming process.

**Table 1.7**
	Calculate Force Constants Once	Calculate Force Constants Always
Number of Points Along IRC	45	70
Final Structure
Energy/a.u.	-231.67806	-231.69166
IRC Pathway
IRC Gradient

The extended number of points on the IRC plot combined with the fact htat hte force constants were calculated at every point meant that a good minimum was reached. In this way, it was possible to compare the energy of the final structure with the literature values and it was clear that the structure present was indeed the Gauche 2 structure. Despite this not being the lowest energy conformer it is still a very good result. If there had been more time available it would have been interesting to see whether a different minimum would have been reached when using the boat transition state structure.

Calculating Activation Energies

The last aspect of this section of the investigation was to calculate activation energies for the reaction via both transition state structures. This was done by reoptimising the structures using the higher level B3LYP/6-31G method and running frequency analysis to obtain thermodynamic data. The DFT technique was used instead of the hartree fock method because of its more rigourous approach, which ultimately leads to more accurate results.

	HF/3-21G			B3LYP/6-31G
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298K		at 0 K	at 298K
Chair TS	-231.619	-231.466	-231.461	-234.556	-234.414	-234.409
Boat TS	-231.602	-231.450	-231.445	-234.543	-234.402	-234.396

Using this data it was possible to calculate the activation energies for both transition state structures at 0K and 298K (Table 1.9).

Table 1.9 - Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G	B3LYP/6-31G	Experimental
	at 0 K	at 298K	at 0 K	at 298K	at 0 K
ΔE (Chair)	45.71	44.69	34.06	33.16	33.5
ΔE (Boat)	55.61	54.76	41.96	41.32	44.7

The results for the B3LYP/6-31G method show better consistency with the experimental results.

Diels Alder Cycloaddition

This section of the experiment involved characterising the transition state of the Diels-Alder transition state using previously discussed techniques. The reaction is a [4 + 2] pericyclic cycloaddition reaction between a conjugated diene and a dienophile. Reactions of this sort have no intermediate and pass through a concerted transition state.

The HOMO/LUMO of the diene reacts with the HOMO/LUMO of the dienophile to form two new σ bonds. The number of π electrons involved in these pericyclic transition states control if the reaction proceeds via a concerted stereospecific way or not, allowed or forbidden. The π orbitals of the dienophile react with the π orbitals of the diene to form new σ bonds. Whether or not the reaction is concerted depends upon the number of π electrons. the reaction is said to be allowed if the HOMO of one species can interact favourably with the LUMO on the other.

The first example of a Diels-Alder reaction investigated was between ethylene and cis-butadiene. The second example examined was the stereoselectivity of the reaction between cyclohexa-1,3-diene with maleic anhydride, which is another example of a Diels-Alder reaction.

Reaction between Cis-Butadiene and Ethylene

Optimisation and Molecular Orbitals of Reactants

Cis-butadiene and ethylene were optimised using the semi-empirical AM1 method, from which a HOMO and LUMO were drawn for each molecule (Table 2.1). This was done so that the symmetry for each orbital could be considered in order to decide whether the reaction is permitted or not.

**Table 2.1**
	Cis-Butadiene		Ethylene
	HOMO	LUMO	HOMO	LUMO
Molecular Orbital
Symmetry	Antisymmetric	Symmetric	Symmetric	Antisymmetric
Energy/a.u	-0.344	0.017	-0.388	0.053

The results shown in Table 2.1 clearly display the constraints on the HOMO/LUMO interactions. Such that HOMO-LUMO interactions are possible but HOMO-HOMO or LUMO-LUMO are not due to symmetry considerations.

To confirm that the optimised structures were in fact minima, frequency analysis was carried out. This showed that in the case of ethylene there are no negative frequencies, highlighting that a minimum had indeed been reached. In the case of cis-butadiene there was a negative frequency (-35.89cm^-1), which can be attributed to a rotation about the central C-C bond that can happen freely at room temperature. The negative frequency highlights that this structure is a maximum, as expected, due to the syn-periplanar arrangement which results in significant A1,4 strain. The planar conformation of cis-butadiene is the one modelled because it is the reactive one.

Transition State Optimisation

The transition state was drawn in GaussView and optimised. Molecular orbitals were then calculated to confirm that the symmetry requirements of the reactants' molecular orbitals are correct. The previously optimised structures of ethylene and butadiene were copied into a new window and arranged such that they resembled an envelope. A freezing method, which has been used earlier, was used to optimise the transition state. A TS berny method was subsequently used to perform an Opt+Freq calculation. these two different techniques were run using two different methods (AM1 and DFT/B3LYP/6-31G).

The key imaginary vibration that can be associated with the formation and breaking of diels alder reaction is the same for all methods, despite the different frequencies observed.

**Table 2.2**
Method	Semi-empirical/AM1 - Frozen Coordinate Method	Semi-empirical/AM1 - TS (Berny)	DFT/B3LYP/6-31G(d) - Frozen Coordinate Method	DFT/B3LYP/6-31G(d) - TS (Berny)
Optimised Structure
Energy/a.u.	0.11165	0.11165	-234.546	-234.495
Imaginary Frequency/cm^-1	-956	-955	-525	-535

There is a stark difference between the two computer basis sets due to the level of accuracy associated with each of them. The differing methods used, despite not beign able to be directly compared against each other, produce different results. Bond lengths can be compared and the DFT method resulted in an increase in the terminal carbon bond length. The vibration is the same for all despite the varying frequencies. From the literature, a C-C bond length is 1.54 Å and a sp² C=C bond is 1.34 Å. When these were compared to the values seen in the transition state it was noted that the transition state bond lengths were allmost all uniform and inbetween the two afformentioned figures. This shows that, as expected, the carbons are between sp² and sp³ hybridisation.

Molecular Orbital Analysis

**Table 2.3- Molecular orbitals obtained from AM1 and Berny TS**
	HOMO	LUMO
Molecular Orbital
Energy/a.u.	-0.324	0.023
Symmetry	Antisymmetric	Symmetric

It is clear that the HOMO of the transition state was formed from the overlap of the HOMO of cis-butadiene and the LUMO of ethylene. From the diagram it wass possible to see the σ bonding orbitals of the C-C bonds formed in the reaction. The LUMO of the transition state was formed from the overlap of the HOMO of ethylene and the LUMO of cis-butadiene. From the diagram it is possible to see the σ* antibonding orbitals. As a result, the diagrams are in good agreement with the conversation of orbital symmetry, which requires that the symmetry of an orbital must be the same as its prerequisite orbitals.

Cyclohexa-1,3-diene and Maleic Anhydride

This section of the investigation concerns the stereoselective Diels Alder cycloaddition between maleic anhydride and cyclohexa-1,3-diene (Figure 5). Through a kinetically controlled reaction two products are formed, the dominant one being the endo product. These computational calculations will shed light on the regiochemistry observed as well as why the endo product is the preferred product.

Figure 5 - Endo and Exo products

Optimising the Reactants

Cyclohexa-1,3-diene and maleic anhydride were drawn in GaussView and optimised using the semi-empirical method of AM1. This enabled the molecular orbitals of each molecule to be obsvered and thus the HOMO and LUMO were drawn. From these molecular orbitals it is possible to assertain which will interact to form product. The salient point is that the symmetry of the orbitals must be conserved and only orbitals of the same symmetry are able to interact. In this way the cyclohexadiene LUMO and the maleic anhydride HOMO or the cyclohexadiene HOMO and the maleic anhydride LUMO must interact to reach the transition state. The former interaction would result in an overall symmetric scenario, whilst the latter interaction would result in an overall antisymmetric scenario.

**Table 2.4**
	Maleic Anhydride		Cyclohexa-1,3-diene
	HOMO	LUMO	HOMO	LUMO
Molecular Orbital
Energy/a.u.	-0.4419	-0.0595	-0.3256	0.01381
Symmetry	Symmetric	Antisymmetric	Antisymmetric	Symmetric

Optimizing the Transition State

The exo structure was drawn by copying into a new window the previously optimised reactants. The bonds between the reacting carbons were frozen to 2.2 Å using the Redundant Coord Editior and an Opt+Freq calculation was carried out to a minimum. An AM1 calculation with additional keywords:Opt=NoEigen inserted. The endo structure was obtained by using a similar technique.