Physical Chemistry Computational Labs

The Cope Rearrangement

The Cope rearrangement involves a thermal pericyclic [3, 3] sigmatropic rearrangement of 1, 5 dienes to form a regioisomeric diene ^[1]. Although it is a concerted reaction, it can be described as going through a high-energy transition state which explains the requirement of thermal energy for the isomerisation to occur^[2]. This transition state can take the form of either a chair or boat conformation, depending on the stereoelectronics of the two double bonds; they will overlap in the most favourable electronic conformation regardless of sterics.

Optimising Gauche and Anti forms of 1, 5 Hexadiene

1, 5 hexadiene one of the few molecules which can undergo the Cope rearrangement to produce the same product as the original reactant. The reaction scheme of the rearrangement is shown in the diagram in the section above. The molecule has free rotation around the single bonds of the molecule, which comprise of three of the five caron-carbon bonds. Therefore they are allowed to be in either gauche (with a dihedral angle of 0⁰) or antiperiplanar (with a dihedral angle of 180⁰) conformations with regards to each other.

Anti-Conformation

Molecule 1: DOI:10042/to-4806 Molecule 2: DOI:10042/to-4807 Molecule 3: DOI:10042/to-4808

The anti-conformation of the molecule has the bonds between four the non-terminal carbon atoms all in the antiperiplanar conformation. Thus, the dihedral angle between carbons atoms no. 9 and 7 in the molecule to right right should be around 180^o. This is generally a lower energy conformation than the gauche conformer (further explored below) due to the minimisation of steric strain.

The structure of several variations of the anti-conformer was drawn in Gaussview, the dihedral angle between atoms 9 and 7 set to 0^o and the structure cleaned up. It was then optimised on the Gaussian interface with the Hartree-Fock method and a low-level 3-21G basis set. The results are displayed in the table below. As shown in the table, the lowest energy conformations are jointly the C₁ and C_i conformers (although the Ci conformation is slightly lower in evergy than the C1 one). As all the molecules are in the anti conformation, this difference in energy is entirely due to the lack of free rotation around the carbon=carbon double bonds; as these are fixed in orientation, they can give rise to geometrical isomers which are more or less energetically favourable depending on steric constraints.

Table to show the relative energies and point groups of the anti- conformers of 1, 5 hexadiene
Point Group	Energy/Hartrees	Relative Energy/kcal/mol
C₁	-231.69253	0.0003
C₂	-231.69260	0.00006
C_i	-231.69253	0.0003

Gauche Conformation

Molecule 1: DOI:10042/to-4808 Molecule 2: DOI:10042/to-4809 Molecule 3: DOI:10042/to-4815 Molecule 4: DOI:10042/to-4816 Molecule 5: DOI:10042/to-4818 Molecule 6: DOI:10042/to-4817

File:Hexadiene gauche 2 opt.jpg

On the other hand, for the gauche conformation, the four internal carbon atoms are all gauche to each other. This should result in an dihedral angle between carbons 8 and 1 shown in the image to the right of 0^o, but due to bond strain, this is practice usually around 60^o.

As with the anti- conformer, the carbon-carbon bonds adjacent to the double bonds were rotated to obtain different geometrical conformations of the gauche conformer. These were then optimised in Gaussian with the Hartree-Fock method, the same basis set as for the anti- conformers: 3-21G.

As expected, the majority of the gauche conformers are higher in energy than the anti-conformers. This is due mainly to the steric strain of having the more bulky carbon chains rather than smaller hydrogen atoms in closer proximity to each other. However, the lowest overall conformation (Molecule no. 6) is actually in the gauche conformation. This is because it is in the perfect position to undergo the reversible Cope rearrangement, and can thus interconvert between two isomeric forms, reducing its energy.

Table to show the relative energies and point groups of the anti- conformers of 1, 5 hexadiene
Diagram	Point Group	Energy/Hartrees	Relative Energy/kcal/mol
	C₁	-231.48163	0.21
	C₁	-231.69153	0.001
	C₁	-231.68961	0.003
	C₁	-231.68916	0.004
	C₁	-231.69166	0.001
File:Hexadiene gauche 6 opt.jpg	C₁	-231.69266	0.0

Futher optimisation of Anti- Conformer

6-31G Optimised version of anti- conformer: DOI:10042/to-4832

The lowest energy anti-conformer was further optimised with a higher-level basis set, the 6-31G d. A different method, B3LYP, was also used instead of the Hartree-Fock method. This allowed us to obtain a more accurate representation of the molecule orbitals. The result was a molecule that was very similar in geometry to the original molecule, but with a very different energy. Although the assumption is that the B3LYP method found a lower-energy minimum than the Hartree-Fock mechanism, as a different basis set was used, the energies cannot be directly compared.

However a summary of the different energetic contributions can be obtained:

Summary of energetic contributions
Energy Contribution	Energy/a.u.
Sum of electronic and zero-point energies	-234.41623
Sum of electronic and thermal energies	-234.40895
Sum of electronic and thermal enthalpies	-234.40800
Sum of electronic and thermal free energies	-234.44780

Chair and Boat Transition States

The Cope rearrangement can go via either a chair or boat transition state, resulting in two potentially different transitional geometries and activation energies. The following section will explore the two transition geometries and their respective energies.

Chair Transition State

The optimum geometry for the chair transition state will be calculated by exploring two different methods; the Hessian calculation, which computes the force constants at the beginning of the calculation, and the Redundant Coordinate Editor, which works by freezing the fragments at a particular distance and optimising the geometries from there. Both are optimised from two allyl (CH₂CHCH₂) fragments.

Hessian calculation:

Allyl group optimisation: DOI:10042/to-4819 Chair TS Optimisation: DOI:10042/to-4820

File:Frequency 1.JPG

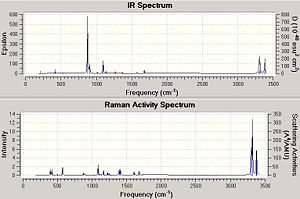
The Hessian calculation, as mentioned above, works by computing the force constant matrix in the first step of the calculation to determine the reaction coordinate. However, this is only possible if the geometry of the system to be optimised is already very similar to that of the final transition state.

To determine the transition state, the two allyl fragments combined in an orientation similar to that of the potential chair transition state, with the terminal carbon atoms approximately 2.2A apart. They were then optimised to a 'Berny' transition state, with the force constants calculated only once. To take take vibrational modes of motion into account, a frequency calculation was run simultaneously. As before, the calculation was run on the Gaussian interface with the Hartree-Fock method and 3-21G basis set.

Table to show Summary of data for Hessian Calculation
Molecule	Energy	Vibrational frequency	Intensity
	-231.65 Hartree	-817.91 cm^-1	5.85 esu²cm²

The energy was found to be -231.6158, 0.07653 Hartree higher in energy than the anti- conformation of the reactant. A negative vibrational frequency of -817.91 cm-1 was found, signifying the negative curvature of a transition state. As shown in the image above, this frequency corresponds to the stretching of the terminal carbon atoms on each fragment towards and away from each other, signifying the transition state of the Cope rearrangement.

Frozen Coordinate Calculation:

Chair TS Optimisation 1: DOI:10042/to-4821 Chair TS Optimisation 2: DOI:10042/to-4822

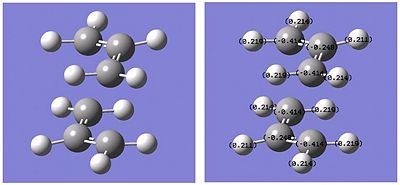
To use the Frozen coordinate method, the two allyl fragments were introduced as before. However, this time a bond distance was specified between the two terminal carbons of each allyl chain to the other, giving a rough estimate of the distance between them. Instead of optimising to a transition state, the system was calculated to optimise for a minimum with the same Hartree-Fock method and 3-21 basis set.

After the first optimisation, the total energy of the system was found to be identical to that calculated by the Hessian calculation shown above. Now the geometry had been optimised, the distance between the terminal carbon atoms of the two allyl fragments was optimised also by 'unfreezing' the bonds and running the same calculation to a minimum. This time, the energy was further reduced, suggesting an even more stable transition state.

Although the second optimisation did not significantly alter the geometry of the transition state, the NBO analysis below shows a significant difference in the charges and a small stabilisation of the zero-point energies. The terminal carbons on the allyl fragments have aquired a much higher level of electron density in comparison to the internal carbon atoms. This suggests the formation of a new bond between the terminal carbon atoms of the allyl fragments, as occurs in the Cope rearrangement.

Table to show Summary of data for Frozen Coordinate Calculation
Optimisation no.	Energy/Hartree	C1 Charge density	C2 Charge density	H1a Charge density	H1b Charge density	H2 Charge density
		-231.61518	-0.414	-0.248	0.219	0.214	0.211
		-231.61932	-0.433	-0.225	0.224	0.218	0.207

Boat Transition State

Boat TS Optimisation attempt 1: DOI:10042/to-4824 Boat TS Optimisation attempt 2: DOI:10042/to-4823

File:QST2 2.JPG

The Boat transition structure was optimised with the QST2 method, where the reactant and product are specified and Gaussview calculates the conformation of the lowest energy transition state. Conversely to the Hessian and Frozen Coordinate methods, the QST2 method starts from the full anti- conformation of 1, 5 hexadiene instead of two allyl fragments. The starting material, a 6-31G optimised molecule, was appended into Gaussview. The product, which coincidentally was also 1, 5 hexadiene, was added. To differentiate the two molecules so Gaussview would read that the rearrangement had occurred, the labels stating the numerical order of each carbon and hydrogen atom were altered. A frequency optimisation was then run with the Hartree-Fock method and 3-21G basis set as before.

However, like the Hessian method, the QST2 method requires that the input geometry be fairly similar to that of the transition state calculated. The fact that the reactant and product were so geometrically different resulted in the failure of the calculation shown above.

To make the reactant and product more accurately model the boat transition state, the angles of the bonds in the anti-conformer were altered to bring them closer to transition state geometry. The dihedreal angle of the four central carbon atoms was altered from approximately 180^o to 0^o, more approximating a gauche conformation. The internal angles were then all set to 100 to give the two molecules shown above to the right.

This time, the frequency optimisation returned intact and gave the boat transition state shown to the left. As expected, the energies were slightly higher than that for the chair conformation due to the higher proportion of gauche bonds and the resulting steric strain.

Table to show Summary of data for QST2 Calculation
Molecule	Energy	Vibrational frequency	Intensity
	-231.60280 Hartree	-840.09 cm^-1	27.02 esu²cm²

Chair IRC

Minimisation 1: DOI:10042/to-4826 Minimisation 2: DOI:10042/to-4829 Minimisation 1: DOI:10042/to-4827 Minimisation 2: DOI:10042/to-4828

Simply by analysing the chair and boat transition state geometries calculated in the previous section, it is not possible to predict the original reactand and final product conformations. However, by making small optimisations to minimise the energy around the negative curvature of the transition state, an optimised geometry of the product can be predicted. As the Cope reaction has a symmetrical energy curve, this is also the geometry of the reactant.

The Intrinsic Reaction Coordinate works by making small optimisations to the geometry of the transition state, calculating the energies and gradient at every step and predicting the next geometry that will result in the largest decrease in energy and therefore steepest gradient. Therefore, the more steps in the calculation and the more frequently the force constants are calculated, the more accurate the minimisation. The downsides to carrying out the more complex, higher-step calculations are the longer time taken and potentially larger cost.

To run an initial Intrinsic Reaction Coordinate calculation (Method 1 in the table below), the IRC method was used. Due to the symmetrical energy diagram of the Cope Rearrangement and to save time, this was only calculated in the forward reaction. The default of a 50 step calculation was selected. However, the resulting energy and gradient profiles showed that a minimum had not been reached, and further optimisation needed to be done to achieve this. Three different methods were used, the results of which can be observed in the table below:

Method 2: The lowest-energy geometry of the calculation run with Method 1 was taken and optimised further to a minimum. This was done with the Hartree-Fock method, and a low-level 3-21G basis set.

Method 3: The number of steps allowed to run in the calculation was increased to 400, resulting in a much lower energy minimum and a gradient closer to 0.

Method 4: Force constants were calculated at each step instead of only at the start of the calculation. This gave a calculation which took much longer to run but gave very accurate results, reaching a clear minimal energy and a gradient of 0.

Table to show different IRC methods and their accuracy
Method	Details	Image	Accuracy	Energy and IRC Gradient Graphs
0	Chair transition state before minimisation of energy		No minimisation
1	50 steps. Force constant calculated once.		Energy does not reach minimum as gradient is above 0. Requires more steps. Gradient = 7.28 x 10^-4
2	Minimum energy conformation from Method 1 taken and optimised.		Energy appears to reach minimum in a series of short steps. Gradient = 7.01 x 10^-5
3	500 steps. Force constant calculated once.		Energy does not reach minuimim, but gradient is lower than for previous calculation. Gradient - 2.93 x 10^-5	File:Chair TS IRC 2 image a.jpg
4	500 steps. Force constants calculated at every step.	File:Chair TS IRC 3 image.jpg	Gradient reaches 0. Energy is fully minimised. Gradient = 1.15 x 10 ^-5	File:Chair TS IRC 3.JPG

From the data shown in the table above, it appears that methods 2 and 4 result in the lowest energies, with geometries closest to that of the product. However, their geometries are subtly different, suggesting that as method 1 did not include the calculation of force constants at every step, its resulting lowest geometry, which was then minimised further with method 2, was not in fact the optimum geometry.

Further Optimisation of Transition States and Calculation of Activation energies

Optimisation of Chair TS: DOI:10042/to-4830 Optimisation of Boat TS: DOI:10042/to-4831

The activation energies of the two transition states can be calculated by taking potential energies from the Gaussian logfile. To do this accurately requires a larger basis set than the 3-21G, so the chair and boat transition state geometries obtained in the previous section were optimised again with the DFT/B3LYP method and 6-31G basis set. It was noted that the geometries were very similar to those obtained by the lower-level 3-21G basis set, but that the energies were significantly different. Comparison with the energetics data from the original anti- reactant yielded the activation energies of both transition states, shown in the table below.

Table to show the relative energies of boat and chair transition states
Transition state conformation	Energy at 0K	Energy at 298K	Activation energy at 0K	Activation energy at 298k
Chair	-234.41492	-234.40900	33.61 kcal/mol	40.71 kcal/mol
Boat	-234.40234	-234.39600	32.56 kcal/mol	40.09 kcal/mol

As shown in the table above, the boat conformation is higher in energy also when optimised by the 6-31G basis set as when the 3-21G is used. This leads to a higher activation energy to from the boat transition state; it is almost 10 kcal/mol higher in energy than the chair transition state both at 0 and at 298K. For both conformations, the activation energies are higher at 0 K than 298 K as at higher temperatures, the transition state is stabilised compared to the energy of the lower energy reactant, resulting in a larger activation energy.

References

↑ A. C. Cope et al, J. Am. Chem. Soc., 1940, 62, 441
↑ R. K. Hill, Comp. Org. Syn., 1991, 5, 785-826.

[1] A. C. Cope et al, J. Am. Chem. Soc., 1940, 62, 441

[2] R. K. Hill, Comp. Org. Syn., 1991, 5, 785-826.

[1]

[2]