Rep:Mod3:bhheller

Module 3: The Transition State

Benjamin Heller

The Cope Rearrangement

Cope Rearrangement

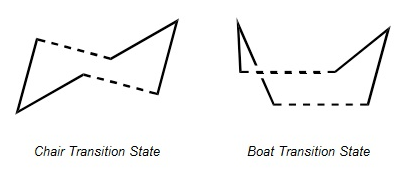
The Cope rearrangement goes by a [3,3]-sigmatropic shift rearrangement and has been the subject of numerous experimental and computational studies. For a long time its mechanism was the subject of some controversy. However, now it is generally accepted that the reaction occurs in a concerted fashion, in which one σ-bond is formed while another is broken simultaneously, via a transition state with either a "chair" or a "boat" geometry, with the "boat" transition structure lying several kcal/mol higher in energy. The two transition states are shown below:

Optimising the Reactants and Products

The structures of several conformers of the 1,5-hexadiene reactants and products were optimised in GaussView using the HF/3-21G level of theory and then symmetrised it to find the point groups. The results are shown in the table below.

Conformer		Energy (a.u.)	Point Group
anti 1	anti1	-231.69260209	C2
anti 2	anti2	-231.69253530	Ci
gauche 1	gauche1	-231.68771616	C1
gauche 3	gauche3	-231.69266122	C1

The gauche conformers are higher in energy than the anti conformers the carbons are as far away from each other as possible. The molecule will adopt an anti conformation as it has less steric repulsion and so is more stable. The gauche 3 conformer is is the most stable due to a C-H σ* - C=C π orbital overlap that is possible in this configuration.

The anti 2 conformer was first optimised using the same method and basis set and then again, this time using the more complex B3LYP/6-31G* DFT level level of theory. A comparison of the two structures is shown in the table below.

Comparison of geometries for anti 2 conformer

	HF/3-21G	B3LYP/6-31G*
Point group	Ci	Ci
Energy (a.u.)	-231.69253530	-234.61171035
C=C bond length (Å)	1.32	1.33
sp2C-sp3C bond length (Å)	1.51	1.51
C-C bond length (Å)	1.55	1.55
C1-C2-C3 angle (o)	124.8	125.3
C2-C3-C4 angle (o)	112.6	112.7

The energy for the B3LYP/6-31G* method is more negative, however, comparisons shouldn't be made between different levels of theory. The symmetry remains the same between the two molecules but the bond lengths change except from the central C-C bond. The bond lengths are slightly larger for the B3LYP/6-31G* optimised structure suggesting the atoms are more spread out reducing steric instability which could could account for the possibly lower energy.

A frequency calculation was run to confirm that the structure was indeed a minimum. This was the case as there were no negative (imaginary) vibrations. Some selected vibrations are assigned below as the IR spectrum is also shown.

IR spectrum of hexadiene

Selected vibrations of optimised anti 2 conformer

Frequency	Animation	Intensity	Assignment
1728.5		20	asymmetric C=C stretch
3027.6		59	symmetric vinyl C-H stretch
3080.4		37	asymmetric vinyl C-H stretch
3139.4		60	alkene C-H stretch
3159.0		14	asymmetric alkene C-H stretch
3243.8		56	symmetric alkene C-H stretch

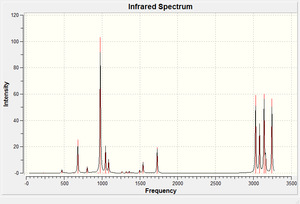
From the log file the energy of the molecule can be separated into potential and kinetic energy parts and from there the enthalphy and free energy of dissociation can be calculated. These parameters are temperature-dependent and so a calculation was run at 0 K as well as 298K to study the effect of temperature on the various energies, the results are tabulated below:

Energies (a.u.)	298K
Zero-point correction	0.142507
Thermal correction to Energy	0.149853
Thermal correction to Enthalpy	0.150797
Thermal correction to Gibbs Free Energy	0.110933
Sum of electronic and zero-point Energies	-234.469204
Sum of electronic and thermal Energies	-234.461857
Sum of electronic and thermal Enthalpies	-234.460913
Sum of electronic and thermal Free Energies	-234.500777

The Sum of electronic and zero-point Energies is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE).

The Sum of electronic and thermal Energies is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + Evib + Erot + Etrans).

The Sum of electronic and thermal Enthalpies contains an extra correction for RT (H = E + RT), which is particularly important when looking at dissociation reactions.

The Sum of electronic and thermal Free Energies includes the entropic contribution to the free energy (G = H - TS).

Optimising the "Chair" and "Boat" Transition Structures

Computational Modelling can be used to model and hence investigate the transition state of the Cope Rearrangement in detail. There are two possible transition state configurations; the chair or the boat.

"Chair" Transition Structure

The chair transition state was modelled and then optimised using two different methods; optimisation to a TS(Berny) by computing the force constant once and then Frozen Coordinate method, by using the redundant coordinate editor. The first step in both cases optimise an allyl fragment at the HF/3-21G level of theory and then to arrange two of them in an approximate chair transition state separated by a distance of 2.2Å. This was then optimised again at the HF/3-21G level of theory using the two methods.

Chair TS
Chair TS

TS(Berny) method

The approximate structure for the transition state needs to be accurate as this method is very sensitive to the structure of the input and will not be able to optimise the correct TS if the input is not good enough. However, the transition state structure is known and so this method is works well and is reasonably easy. This method works by computing the force constant matrix (Hessian) in the first optimisation step and then constantly recalculated as the optimisation proceeds. If a poor input structure is used the potential energy surface (PES) curve may be substantially different from the actual transition structure PES and so an incorrect TS structure would be optimised.

The energy of the optimised structure was -231.61932241a.u. and the terminal C-C bond length was 2.02Å. A frequency analysis was also carried out to confirm the successful optimisation as a negative (imaginary) frequency confirms a TS. An imaginary frequency was found at -817.96cm^-1 which corresponds to the Cope rearrangement as there is a vibration along the bond to be formed and an asymmetrical one along the bond to be broken during the rearrangement, this indicates asynchronous bond formation in the pericyclic reaction. For the calculation in GaussView the additional keywords, "Opt=NoEigen" were added to stop the calculation crashing if more than one imaginary frequency is detected during the optimisation, which can often happen if the guess transition structure is not good enough.

Frozen Coordinate method

Firstly, the distance between the two allyl fragments were optimised with the distance between the terminal carbons fixed at 2.2Å. This was done by freezing the reaction coordinate so the rest of the molecule is then optimised around it. The distance between the terminal carbons was then "unfrozen" and the molecule was optimised again. An advantage of this method compared to the force constant calculation is that in the frozen coordinate approach not the whole hessian has to be computed. It is only differentiated along the reaction coordinate. One advantage of doing this, is that it is not necessary to compute the whole Hessian once this has been done, and just differentiating along the reaction coordinate can give a good enough guess for the initial force constant matrix. This can save a considerable amount of time in cases where the force constant calculation is expensive.

This method returns very similar results to the method above with an energy of -231.61932201a.u. and a terminal bond length of 2.02Å. Both methods returned them same results suggesting that they have converged to the same optimisation and that they are both fairly accurate, however, each has it's downsides. For the Frozen Coordinates method a reasonable estimation of the terminal distance between the allyl fragments must be known and for the Hessian method the initial structure has to be reasonably accurate or else the optimisation will fail.

"Boat" Transition Structure

For the optimisation of the boat transition state a different method was used, the QST2 method. This involved specifying the reactants and products for the reaction and then the calculation interpolates between the two structures to try to find the transition state between them. A problem with this method is that both the product and reactant structure have to be drawn so that they are as close as possible to the structure of the transition state otherwise the calculation will no be able to interpolate between them. This was demonstrated during the first optimisation and so the geometries of the reactant and product required modification so that they were closer to the boat transition structure. This was done by changing the central C-C-C-C dihedral angle to 0^o and the inside C-C-C angles to 100^o for both molecules. The molecules from which the transition state was calculated are shown below.

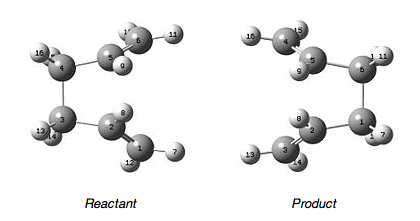
The QTS2 method returned the following results; the energy was -231.60280248a.u. and the terminal C-C bond length was 2.14Å. There was an imaginary frequency, which confirms that it is a transition state. The vibration was at -840.04cm^-1 and corresponds to the asynchronous bond formation of the Cope Rearrangement. The vibration is shown below:

There is another method, the QST3 method, that also allows input of the geometry of a guess transition structure and this can often be more reliable. This calculation was run and gave very similar results, suggesting that the QTS2 method is accurate enough for this example. The energy was -231.60280241a.u. and the terminal C-C bond length was the same, 2.14Å. There was also one imaginary frequency at -839.85cm^-1 which corresponded to the same vibration. The structure of the boat TS is shown below:

Boat TS
boat TS

Intrinisic Reaction Coordinate (IRC) Method

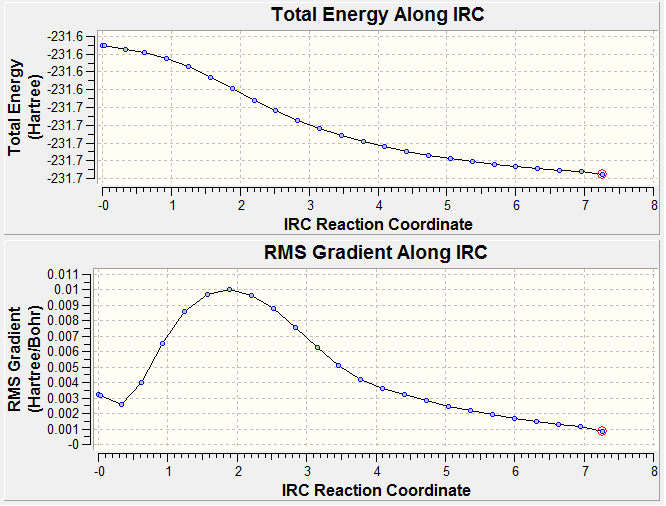
There is a method implemented in Gaussian which allows you to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This is called the Intrinisic Reaction Coordinate or IRC method. This creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest and tells us which conformers of 1,5-hexadiene the transition structures connect. This calculation was run on the HF/3-21G optimised chair with 50 points on the IRC pathway and computation of the force constants only once at the start.

The result of this calculation hadn't' yet reached a minimum geometry as a conformer of 1,5-hexadiene structure was expected but not achieved. The energy of the last step (step 25) was -231.68771100a.u.

The IRC calculation was then run again, but the force constant was calculated at every step. This allows the IRC calculation to tell if it is moving down the minimum energy pathway along the potential energy surface and make changes to this pathway if and when necessary. The result of this calculation was a minimum of energy -231.69165621a.u. which is the same as the gauche 2 conformer from the wiki table of results.

Activation Energies For The Transition Structures

The HF/3-21G optimised structures were optimised to a final TS(Berny) using the more complex DFT/B3LYP/6-31G(d) level of theory and from there the activation energies for the reaction via both transition structures can be calculated. A comparison of the energies of the two TS optimised using the two methods is shown below (all the results below for 0K are taken from the results section of the module 3 wiki):

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298 K		at 0 K	at 298 K
Chair TS	-231.61932201	-231.466705	-231.461337	-234.55698281	-234.414919	-234.409010
Boat TS	-231.60280248	-231.450929	-231.445309	-234.54309304	-234.402340	-234.396005
Reactant	-231.69253530	-231.539539	-231.532567	-234.61171035	-234.469203	-234.461857

From the thermochemical data the activation energies for both transition states and hence there pathways can be calculated. The calculated activation energies are shown below:

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298 K	at 0 K	at 298 K	at 0 K
ΔE (Chair)	45.70	45.942042911	34.06	34.342057174	33.5 ± 0.5
ΔE (Boat)	55.60	56.308206706	41.96	43.058021302	44.7 ± 2.0

For both levels of theory the values computed agree with those quoted in the wiki. It can be seen that that the chair TS is more stable than the boat TS and as a result, the chair TS has a lower activation energy than the boat TS and so, the chair TS is the expected TS for the Cope Rearrangement of 1,5-hexadiene. With the anti 2 conformr as the reactant and the gauche 3 conformer as the product.

The Diels-Alder Cycloaddition

The Diels-Alder reaction is a [4π+2π] pericyclic cycloaddition between an s-cis diene and a dienophile. It is an example of cycloaddition and there are no intermediate species. One of the reasons the Diels-Alder reaction goes so well is that the transition state containing six delocalised electrons and thus has some aromatic character and is therefore more stabilised.

The π-orbitals of the dienophile interact with the π orbitals of the diene to form two new σ-bonds. The number of π-electrons involved in the pericyclic transition state determines whether the reaction goes in a concerted stereospecific fashion (allowed) or not (forbidden).

The following optimisations calculations were run using the semi-empirical/AM1 method and then the DFT/B3LYP/6-31G* level of theory and then used to determine the properites of the reactants and transition states to predict the way in which the reaction will proceed.

cis-Butadiene and Ethylene

Cis-butadiene and ethene react together in a Diels-Alder reaction as shown below:

Reactants

Cis-butadiene and ethylene were optimised using the AM1 semi-empirical method. The energy of the optimised cis-butadiene was 0.04880148a.u. and the energy of ethylene was 0.02619723a.u. The frontier molecular orbitals for the two molecules were also calculated and they are shown below.

Reactant	Molecular Orbital	Picture		Energy (a.u.)	Symmetry
cis-Butadiene	LUMO		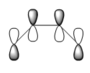	0.017	Symmetric
	HOMO		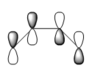	-0.343	Anti-symmetric
Ethylene	LUMO			0.052	Anti-symmetric
	HOMO			-0.387	Symmetric

The symmetries for the HOMO and LUMO orbitals for ethylene are the opposite to those for cis-butadiene so due to the conservation of orbital symmetry the only interaction that can occur are those between the HOMO of cis-butadiene and the LUMO of ethene and the LUMO of cis-butadiene and the HOMO of ethene. This is discussed in more depth later.

Orbital symmetry is important in pericyclic reactions as it determines whether the reaction will proceed and it's stereochemical outcome.

Transition State

The Frozen Coordinates method described above was used to model and optimise the transition state. The optimisation was first run using the semi-empirical/AM1 method with the C-C bond forming distance frozen at 2.1Å. The result was then optimised to a TS(Berny) with unfrozen C-C bond forming distances. It was then finally optimised again to a TS(Berny) using the DFT/B3LYP/6-31G(d) level of theory and the keyword "opt=NoEigen". The results of the last two optimisations are shown below:

Properties	semi-empirical/AM1	DFT/B3LYP/6-31G(d)
Energy (a.u.)	0.11165631	-234.54389654
Imaginary Frequency (cm-1)	-956.92	-524.82
Vibration
C-C Bond Forming Length (Å)	2.12	2.27
Structure	TS

Comparison cannot be made between the energies from the two methods each method reports energies differently explaining the large difference. The larger C-C bond forming length is due to the greater accuracy of the DFT/B3LYP/6-31G(d) method. This larger bond length causes a shallower potential energy slope to the TS maximum leading to a lower imaginary frequency and a lower total energy of the TS.

Both optimisations contain one imaginary frequency confirming that a TS has been found. Although the wavenumber of the vibrations is different in the two transition states it corresponds to the same vibration (shown above) and describes the synchronous formation of two C-C bonds between the termini of the two molecules and thus is characteristic of the Diels-Alder reaction.

A typical sp³C-sp³C single bond length is 1.54Å and a typical sp²C=sp²C double bond length is 1.34Å. In the optimised TS molecules the C=C bond lengths are all 1.38Å and the C-C bond length is 1.40Å suggesting that the π-bonds are breaking to form C-C bonds and a π-bond is forming between the two sp³ carbons. The Van der Waals radius of a C-atom is 1.71Å and the bond forming length is 2.12Å (or 2.27Å for the DFT/B3LYP/6-31G(d) optimised molecule) which is shorter than twice the van der Waals radius of the carbon atom. This means that the atoms are close enough to each other share electron density the bond has not actually been formed yet.

The frontier molecular orbitals of the transition state were calculated and are shown below:

Molecular Orbital		Energy (a.u.)	Symmetry
LUMO		0.023	Symmetric
HOMO		-0.323	Anti-symmetric

It can be seen that the HOMO of the TS comes from the overlap of the HOMO of cis-butadiene and the LUMO of ethene and describes the σ-bonding orbitals of the two C-C single bonds to be formed in the reaction. Where as, the LUMO of the TS comes from the LUMO of cis-butadiene and the HOMO of ethene and describes the σ*-antibonding orbitals. This is consistent with the conservation of orbital symmetry and with MO theory. The conservation of orbital symmetry says that the symmetry of an orbital formed by the overlap of two orbitals must be the same as the symmetry of the initial orbitals. The agreement with MO theory is because occupied orbitals can only interact with unoccupied orbitals which is the case here.

Activation Energy of the Reaction

The reactants were optimised again at the DFT/B3LYP/6-31G* level of theory and the energies were; -155.99594966a.u. for cis-butadiene and -78.52266723a.u. for ethylene. The sum of the energies is -234.52861689a.u. where as the energy of the TS is -234.54389654 a.u. And so, the activation energy is 0.04527965a.u. (118.88 kJ mol^-1) which is in good agreement with the experimental data from the literature which gives the activation energy at 115 ± 8 kJ mol-1 for 0K.

Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

The reaction between cyclohexa-1,3-diene and Maleic Anhydride is also a Diels-Alder reaction. However, unlike the previous reaction, there are two potenial products, the exo and the endo product.

The endo and exo products are diastereomers, and their formation is dependent on the direction of attack by the diene (cyclohexa-1,3-diene) on the dienophile (Maleic Anhydride). The endo isomer is the major product of this reaction and the following calculations will be used to explain this stereoselectivity.

Optimisation of the endo and exo Transition States

The two possible transitions states were optimised using the same three-step method as above for the transition state between cis-butadiene and ethene. The following table shows the results for the optimisations of the TS using both the semi-empirical/AM1 and DFT/B3LYP/6-31G(d):

Comparison of Endo and Exo TS

Properties	endo		exo
	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)
Energy (a.u.)	-0.05150385	-612.68339681	-0.05041953	-612.67931095
Imaginary Frequency (cm-1)	-806.16	-446.91	-812.44	-448.12
C-C Bond Forming Length (Å)	2.16	2.27	2.17	2.29
Structure	endoTS		exoTS

The presence of one imaginary frequency confirms that the optimised structure is a transition state. The vibration, as in the previous section corresponds to the synchronous formation of the two C-C bonds, as expected for cycloadditions, which are concerted reactions. The differences between the results obtained from the two calculation methods is due to the same reasons as discussed earlier.

One would expect the the exo TS to be more stable, and hence the exo product to be the thermodynamic product, as there is less steric clash in this conformation. The steric clash in the endo product, which is present to some extent in the TS, is called 1,3-diaxial compression and is between the hydrogens at the back of the cyclohexen ring and the maleic anhydride.

However, the endo TS is more stable than the exo TS by 0.0041a.u., which is probably due to secondary-orbital interactions in the endo TS which stabilises the structure. This will be discussed later on. The bond lengths of the parts of each fragment not involved in the reaction are very similar, as are the distances between the carbons which form the new C-C bond, with 2.27Å for the endo TS and at 2.29Å for the exo TS.

Another reason for the greater stability of the endo TS could be due to the greater geometric strain felt by the exo TS. In the endo TS, the C-C-C angle along the C=C double bond on the cyclo-1,3-hexadiene unit and the adjacent sp² carbon on the maleic anhydride unit is 99.0°, much closer to the 109.47° expected for the sp³ carbon in the product than the 94.8° in the exo TS.

The distance between the -(C=O)-O-(C=O)- maleic anhydride fragment and the cyclohexene ring in the endo TS is 2.99Å, where as in the exo TS it is 3.02Å away. This shorter distance for the endo could be due to the secondary-orbital overlap in this conformation and is discussed later.

Molecular Orbital	endo			exo
		Energy (a.u.)	Symmetry		Energy (a.u.)	Symmetry
LUMO		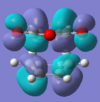-0.067	Anti-Symmetric		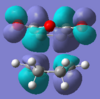-0.078	Anti-Symmetric
HOMO		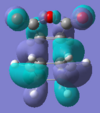-0.242	Anti-symmetric		-0.242	Anti-symmetric

Both the HOMO and LUMO of both TS are anti-symmetric. The HOMO of each describes the σ-bonding interaction to be formed between the terminal carbons of the reactants and products. It is made up by overlap of the HOMO of cyclohexadiene and the LUMO of the maleic anhydride. The LUMO of Maleic anhydride is the π* anti-bonding orbital of the C=C bond and so as it is populated during the cycloaddition the C=C bond breaks, leaving a C-C single bond. The LUMOs of both are entirely anti-bonding between the two fragments.

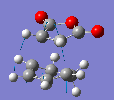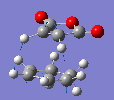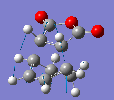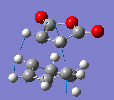
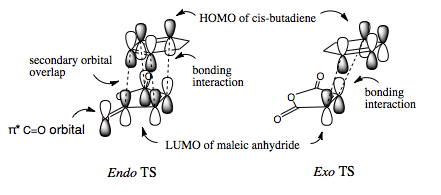
There is a stabilising secondary-orbital overlap present in the orbitals for the endo TS. This interaction is between the central carbons of the conjugated π-system in the cyclo-1,3-hexadiene fragment and the π*-orbital of the C=O bonds from the maleic anhydride fragment. The interaction occurs between in-phase orbital centred in the carbon atom of the π* C=O orbital and the central carbons of the conjugated system, the overlap is from the top face of the π-conjugated system through the back of the molecule to the bottom face of the maleic anhydride fragment and stabilises the endo TS, thus lowering it's activation energy. This interaction can be seen in the picture to the right, and is summarised below. This interaction cannot take place in the exo transition structure as the maleic anhydride fragment points away, and id thus too far away, from the conjugated π-system of the cyclohexadiene and can therefore not interact.

Activation Energy for the Reaction

The reactants were optimised again at the DFT/B3LYP/6-31G* level of theory and the energies were; -233.41892372a.u. for cyclohexa-1,3-diene and -379.28954454a.u. for Maleic Anhydride. The sum of the energies is -612.70846830a.u. From this the activation energies were calculated for the two transition states and the results are summarised below:

Activation Energy	endo TS	exo TS
Activation Energy (a.u.)	0.02507145	0.02915735
Activation Energy (kJ mol-1)	65.8	76.6

This shows that the activation barrier is lower to the endo transition state and so, the reaction pathway to the endo TS and therefore the endo product, goes at a faster rate. Therefore, the endo product will be the major product when under kinetic control with irreversible conditions.

However, the error of the gaussian energy calculations is assumed to be about 5kJ/mol so the difference in the activation energies may not be very precise. This is one of the limitations of Diels-Alder reaction calculations using gaussian as there tends to be little energy difference between different species.

Conclusion

Using these gaussian calculations the transition states of kinetically controlled pericyclic reactions can be accurately represented and can then be used to predict the reactivity of a reaction not only with the stability of the product, but also with the activation energies. Investigation of the molecular orbitals can also give information on stereoselectivity.

One of the problems with Gaussian calculations is that it is only able to calculate energies of the transition states and products to identify the possible kinetic and thermodynamic nature of each. It cannot tell whether the reaction proceeds under kinetic or thermodynamic control so it cannot actually determine which is product is the major product. This can only be done experimentally. Another issue is thatGaussian only runs the calculations on the one molecule, where as, in reality there are many more molecules interacting with each other and each one in a slightly different conformation. A improvement would be to use statistical mechanics and the Boltzmann distribution. A better basis set will also improve the calculations, but this takes more time and resources, so the DFT/B3LYP/6-31G(d) is a good compromise between accuracy and time.