Rep:Mod3:albertfinally

Cope Rearrangement

Optimisation Reactants and Products

Conformations of 1, 5 hexadiene

The table below shows the comparison between the energies and symmetry of the different conformations for 1, 5 hexadiene under HF/3-21G level of theory with reference to Appendix 1. In order to arrange the atoms to reflect the required conformation, the bonds were first broken then moved to reflect the required conformation then followed by re-formation of the bonds in Gaussian.

Properties	Anti-1	Anti-2	Gauche-2
Energy (A.U.)	-231.69260	-231.69254	-231.69153
Symmetry	C1	Ci	C2
Conformational Structure	Pentahelicene	Pentahelicene	Pentahelicene

Comparing the energies of the above conformation, the gauche 2 conformation drawn has a higher energy (i.e. less negative value) than the corresponding anti-1 and anti-2 conformations. From literature , gauche-3 conformation is predicted to be the lowest in energy due to the minimisation of Csp³ - Csp² interaction.

Comparison between Anti-2 Conformation for 1, 5 hexadiene

The table below shows the comparison between Anti 2 conformation for two different Gaussian methods.

Properties	HF/3-21G	B3LYP/6-31G (d)
Energy (A.U.)	-231.69254	-234.61170
Job Time	1 minute 52 seconds	5 minutes 43 seconds
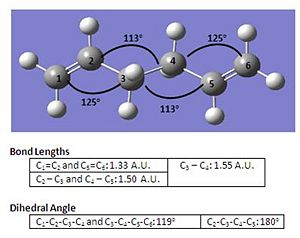
Conformational Structure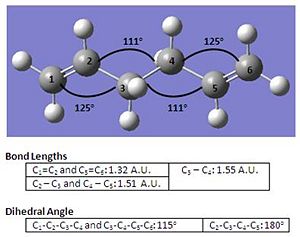

From the table above, it can be observed that while the bond angles and bond lengths show a small difference, however comparing the dihedral angle, there lies a slightly larger difference between both structures which suggests a higher geometric accuracy in the structure at higher optimisation methods. Nevertheless, the trade off in using higher optimisation methods would be the longer time required to finish the job as shown in the above table.

Comparison of thermochemistry of Anti-2 Conformation for 1, 5 hexadiene

The table below shows the comparison of the thermochemistry of the anti-2 conformation for 1, 5 hexadiene at B3LYP/6-31G(*) level of theory. The thermal energies at 0K at B3LYP/6-31G* level of theory can be obtained from DOI:10042/to-2869 . From the table below, it is observed that at 0K, the energies are comparatively higher (i.e. less negative) than at 298.15K which suggests that at 0K the anti-2 conformation is less stable than at 298.15K as more energy is required to overcome the higher vibrational, rotational and translational energies for anti-2 conformation at 0K.

Optimising Chair and Boat Transition Structures

Different approaches to optimising Chair Transition Structure

The table below shows a comparison in the different approaches to optimistion of the chair transition state using a HF/3-21G level of theory at 298.15K and 1atm.

Approach	Optimistion to TS (Berny) [part (b)]	Redundant Coordinate Editor [part (d)]
Bond forming bond length (Å)	2.02008	2.02074
Bond breaking bond length (Å)	2.02034	2.02069
Imaginary Frequency (cm-1)	817.96	817.76
Electronic Energies (Hartrees)	-231.61932244	-231.61932239
Structures	Pentahelicene	Pentahelicene

From the above comparison between the two approaches in optimising the chair transition state of 1, 5 hexadiene, it can be concluded that both approaches result in relatively similar results and thereby the use of optimisation to TS (Berny) i.e. part (b) is sufficient. The consideration for the redundant coordinate editor [part (d)] would be perhaps more useful for more complicated transition states such as in the Diels-Alder reactions as shown later.

Optimising the Boat Transition Structure - QST2 Approach

In this method, it was crucial that the numbering of the atoms in the reactant matches that of the product and secondly the structure of both reactant and product must match each other. Otherwise, the approach will fail.

It was noted that in the course of re-numbering the atoms, the numbers could not be fixed on the atom but rather they would change relative to the number on the other atoms due to the inherent nature of Gaussian. As such, in my approach in re-numbering the atoms, the carbon atoms would first be re-numbered followed by the hydrogen atoms. In this way, it minimised the time required to re-amend the numbers that were previously assigned to the atom.

The structure below shows the Boat Transition Structure with an imaginary frequency of 840.00cm^-1.

Boat QST2 vibration

Pentahelicene

At the imaginary frequency, the two CH₂CHCH₂ units stretches horizontally in the plane of the paper in a concerted asynchronous motion that reflects bond breaking in one terminal carbon and bond formation in another terminal carbon.

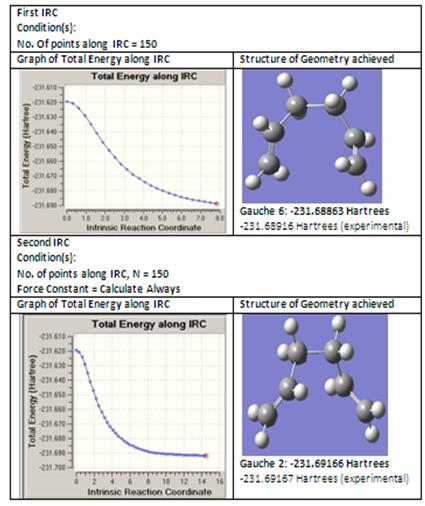
Intrinsic Reaction Coordinate (IRC) for Chair Transition Structure

In this method, a first consideration for the number of points along IRC was set to 150 instead of 50 to obtain a more accurate minimum structure. This can be obtained from:DOI:10042/to-2685 . In the second consideration, the number of points along IRC was set to 150 and the force constants was always calculated. This can be obtained from: DOI:10042/to-2797 .

From IRC, it can be observed that Gaussian has managed to obtain a conformation with a reasonably minimum energy as it follows a minimum energy path. However, comparing with the conformation energies in Appendix 1, the lowest energy conformation should be gauche-3 and not gauche-2 which suggests that for a successful IRC there must be a delicate balance between the number of points along IRC as well as the calculation of force constants.

Activation Energies for both Transition Structures

The table below shows the activation energies for the chair and boat transition structures. The activation energy for the chair transition structure at 298.15K can be obtained from DOI:10042/to-2796 at 0K can be obtained from DOI:10042/to-2875 while for the boat transition structure at 298.15K, it can be obtained from DOI:10042/to-2868 and at 0K, it can be obtained from DOI:10042/to-2876 .

To obtain the activation energy for the boat transition structure, opt=CalcFC was added under Additional Keywords in setting up the Gaussian calculation to calculate the force constant at the first point using B3LYP / 6-31G* level of theory.

To obtain the activation energy, the difference between the sum of electronic and thermal free energies between the chair and anti2 or boat and anti2 structures will be performed. From above, the sum of electronic and thermal free energies for anti2 is -234.50078 Hartrees at 298.15K and -234.49551 Hartrees at 0K. From experiment, the sum of electronic and thermal free energies for anti2 is -234.46920 Hartrees at 0K and -234.46186 Hartrees at 298.15K.

Note: 1 Hartree = 627.509 kcal/mol

Method / Basis Set	B3LYP / 6-31G*	B3LYP / 6-31G*	Experimental
Temperature (K)	298.15	0	0
Sum of electronic and thermal free energies [Chair] (Hartrees)	-234.44271	-234.42588	-234.41492
Sum of electronic and thermal free energies [Boat] (Hartrees)	-234.43175	-234.40535	-234.40234
Activation Energy, ΔE [Chair] (kcal/mol)	36.44	43.69	33.5 ± 0.5
Activation Energy, ΔE [Boat](kcal/mol)	43.32	56.58	44.7 ± 2.0

The values obtained for the activation energy at 0K deviates from the experimental activation energies by about 30% which suggests that the optimised boat and chair transition structures were not the transition structures that reflected the most preferred conformation with the most minimum energy. Nevertheless, what concurs with Appendix 2 is that from the above table, the activation energy for the chair transition state is lower than the boat transition state suggesting that the chair transition state is the more stable and hence more preferred transition state.

Diels-Alder Cycloaddition

Exercise One: Cis-butadiene

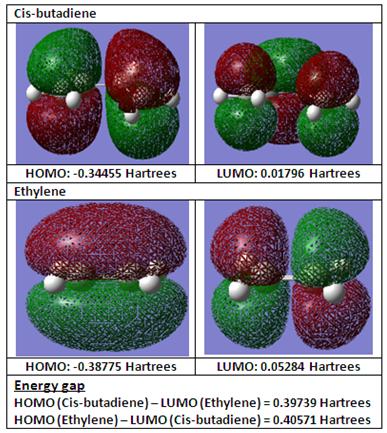
The table below shows the HOMO and LUMO of cis-butadiene.

From the HOMO and LUMO, it can be observed from the orbital arrangement that the HOMO is asymmetric and likewise the LUMO is asymmetric.

Exercise Two: Transition State Geometry of Ethylene and Cis-butadiene

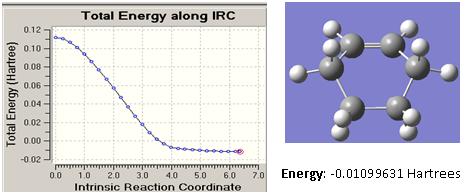
In determining the transition state geometry, Redundant Coordinate Editor with the carbon-carbon bond length of between the ends of both molecules set to 2.1Å by choosing the freeze coordinate option and optimised to TS(Berny) was first employed. This was then followed by using Redundant Coordinate Editor a second time but this time choosing the derivative option. The QST2 method was not successful for this transition state calculation as the reactants and products are largely different.

The energies obtained for both methods using a HF/AM1 level of theory are as follow:

Method	Freeze Coordinate	Derivative Option
Energy (Hartrees)	0.11124	0.11166
RMS Gradient	0.00341520	0.00011676
Imaginary Frequency (cm-1)	No imaginary frequency obtained from Gaussian	957.85

From the imaginary frequency as shown above, it can be observed that for the derivative option, the vibration with respect to the terminal carbon atoms is synchronous where the atoms are stretching perpendicular to the plane of the molecule which reflects bond formation at both ends of the terminal carbons to result in the formation of cyclohexene.

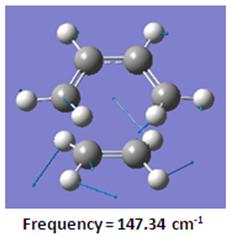
Comparing with the lowest positive frequency of 147.34cm^-1 as shown below, the ethylene rocks in the plane of the molecule while cis-butadiene stretches in the plane of the molecule. which suggests that the lowest positive frequency cannot really be used to predict bond formation and bond breaking in the transition state.

To consider the optimisation at a higher level of theory, the B3LYP/6-31G(*) level of theory was perfomed which can be obtained from DOI:10042/to-2865 . Comparing with the derivative option from above, the energy obtained is -238.54309 Hartrees while the imaginary frequency is at 530.58cm^-1.

Finally, to confirm the transition structure, an Intrinsic Reaction Coordinate (IRC) method was performed using 150 points along IRC, always calculate force constants and always recorrect steps. This can be obtained from DOI:10042/to-2798 .

From the above IRC consideration, the final molecule looks similar to that of the transition state from above and as such the transition structure obtained for ethylene and cis-butadiene is reliable.

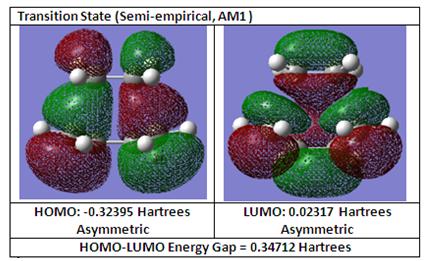
HOMO and LUMO of Transition Structure

From the HOMO and LUMO of the transition structure below it can be observed that the HOMO is asymmetric and the LUMO is also asymmetric. it is also observed that there is significant bonding interactions between the terminal carbons of cis-butadiene and ethylene as observed in the HOMO.

In Diels-Alder reaction, it is the result of an interaction between the HOMO and LUMO of the diene and the dienophile respectively. Considering the HOMO and LUMO of cis-butadiene and ethylene as shown below (performed at semi-empirical, AM1 level of theory), butadiene acts as the diene while ethylene acts as the dienophile.

For this Diels-Alder reaction, it is the HOMO of cis-butadiene that interacts with the LUMO of ethylene due to a favourable orbital overlap between the HOMO of cis-butadiene and the LUMO of ethylene because of similar symmetry which conserves orbital symmetry between the interacting orbitals as described in literature . Furthermore, comparing the energy difference between the HOMO-LUMO interaction, having the HOMO of cis-butadiene and LUMO of ethylene interacting with each other results in a smaller energy gap difference which therefore favours this irreversible Diels-Alder.

Transition State Geometry

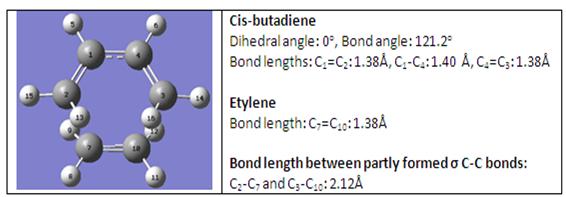
The diagram below shows the geometry of the transition state.

Bond length is the averaged bond distance between two bonded atoms in a molecule. The typical sp³-sp³ C-C bond length is 1.54Å while the typical sp²-sp² C-C bond length is 1.47Å. From literature , the Van der Waals radius of carbon atom is 1.7Å. Comparing with the C-C bond lengths shown in the above table, in particular the partly formed σ C-C bond or sp³-sp³ C-C bond, it is observed that the bond length obtained from Gaussian is indeed longer than the typical sp³-sp³ C-C bond as well as the Van der Waals radius of carbon atom. This longer bond length is a reflection of the angle in which cis-butadiene orientates itself with respect to ethylene to allow for a favourable HOMO-LUMO orbital interaction for this Diels-Alder reaction.

Exercise Three: Regioselectivity of Diels-Alder Reaction between Cyclohexa-1,3-diene and Maleic Anhydride

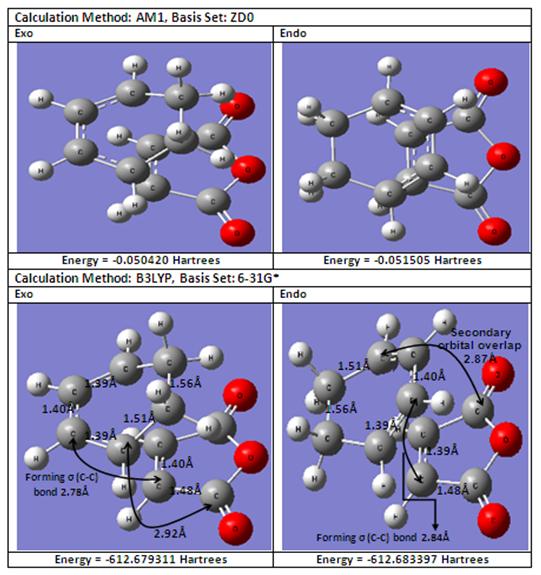
For this Diels-Alder reaction, it is the HOMO of the cyclohexadiene (i.e. the diene) and the LUMO of the maleic anhydride (i.e. the dienophile) that will interact with each other to produce the Diels-Alder cycloadduct. The table below shows the comparison of energies and C-C bond lengths between the endo and exo transition states for the Diels-Alder reaction using two different methods. For the B3LYP/6-31G(*) level of theory, the optimisation of the endo transition state can be obtained from DOI:10042/to-2861 while the optimisation of the exo transition state can be obtained from DOI:10042/to-2731 .

From the above table, it can be concluded that the endo product will be favoured in this kinetically favoured irreversible Diels-Alder reaction as the exo product is higher in energy (i.e. less negative). Comparing the spaitial C-C bond lengths of the forming C-C σ bonds, it can be observed that for the endo transition state, despite having a longer forming C-C σ bond than its exo counterpart, however for the endo transition state there exists a secondary orbital overlap which stabilises the endo transition state thereby favouring the endo product.

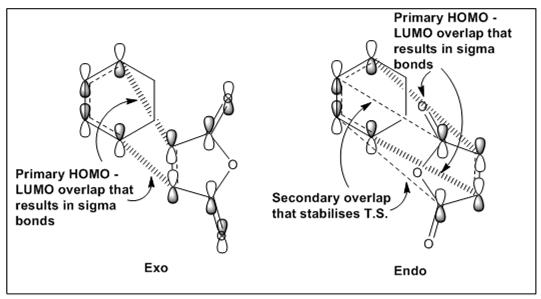
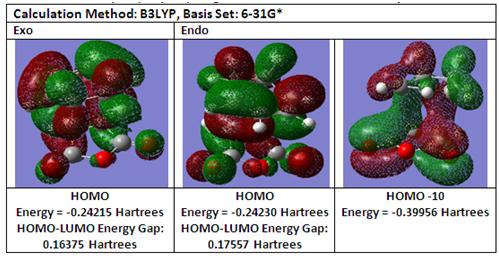
Secondary Orbital Overlap

From the above diagram, comparing both endo and exo transition states, it can be observed that only for the endo transition state, there exists a favourable secondary orbital overlap between the carbonyl carbon in maleic anhydride and another carbon atom on cyclohexadiene which stabilises the endo transition state due to the closer proximity between these two carbon atoms of 2.84Å for the endo transition state as compared to 2.92Å for the exo transition state.

Comparing the HOMO between -(C=O)-O-(C=O) - fragment and the remainder of the system as shown below, it is observed that for the carbonyl carbon for the endo transition state, the orbital on the adjacent carbon atom that forms the σ C-C bond extends to the carbonyl carbon thereby suggesting that the carbonyl carbons on -(C=O)-O-(C=O)- fragment interact with the "opposite" CH₂CH₂ fragment on cyclohexadiene as further observed in the different sizes in the orbital lobes when compared to the exo counterpart.

Considering the nodal properties between the -(C=O)-O-(C=O) - fragment and the remainder of the system as shown below, for the endo transition state, it is observed that the nodal plane extends to remainder of the system due to some bonding interaction between the C=O group and the oxygen atom on the -(C=O)-O-(C=O)- fragment. Comparing with the exo transition state, this bonding interaction is not observed due to a smaller orbital lobe on the oxygen atom on the -(C=O)-O-(C=O)- fragment and as such the nodal plane between the C=O groups in the exo transition state does not extend to the remainder of the fragement. Hence for the endo transition state there exists two nodal planes one between the diene and dienophile and the other through the molecule while for the exo transition state, there only lies one nodal plane between the diene and dienophile.

In order to fully appreciate the effects of secondary orbital overlap, consider HOMO-10 for the endo transition state which shows the overlap between the -(C=O)-O-(C=O)- fragment and the remainder of the system. It is observed that for only the endo transition state, the orbital lobes on the forming σ C-C bond extends to both the carbonyl carbons on maleic anhydride as well as to the carbon atoms on the forming C=C bond in a π_C=C and π*_C=O orbital overlap which demonstrates secondary orbital overlap as described from literature .

Diels-Alder reaction depends on steroelectronic, sterics and regioselective factors. For Gaussian calculation, the issue of sterics is dependent on how the atoms are first drawn relative to each other. As such, sterics consideration can only go so far. Regioselective considerations is not an inherent feature of Gaussian as Gaussian cannot generate a series of isomeric structures for consideration. Rather it depends on the inituitive nature of the person performin the calculation to deduce whether does this Diels-Alder reaction give rise to enantiomers or diastereomers.

Conclusion

From this computational exercise, the transition state of the Diels-Alder reaction was studied in closer detail to observe the stereoselective formation of specific products and thereby complementing the theoretical analysis of stereoselective product formation.