The Transition State

The computational experiments involved the characterisation of transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions.

However, the molecular mechanics/force field methods that works well for structure determination (as in Module 1) cannot be used to study transition states in large molecules, as they do not describe bonds being made and broken, and changes in bonding type and electron distrbution. Instead, molecular-orbital based methods were used to solve the Schrodinger equation numerically and locate transition structures based on the local shape of potential energy surfaces. As well as showing what the transition states look like, reaction paths and barrier heights were also calculated.

The Coper Rearrangement Tutorial

The Cope rearrangement of 1, 5-hexadiene, which specifically involves a [3, 3] sigmatropic shift rearrangement, was studied to locate the low-energy minima and transition structures on the C₆H₁₀ potential energy surface, so that the preferred reaction mechanism could be determined.

It has been argued whether the mechanaism is concerted, stepwise or dissociative but it is now generally accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the boat transition structure lying several kcal/mol higher in energy. By using the B3LYP/6-31G* level of theory in Gaussian, the activation energies and enthalpies were calculated, which were then compared with literature values.

Optimising the Reactants and Products

Optimisation of 1, 5-hexadiene with an "anti" linkage for the central four C atoms was performed using the HF/3-21G level of theory and symmetrized to find its point group. Vibrational frequencies were then calculated and visualised, and potential energies corrected in order to compare them with experimental values. The same calculations were performed with another molecule of 1, 5-hexadiene with a "gauche" linkage, which would be expected to have a higher energy due to steric repulsion betweem the eclipsing carbon atoms. .

Results of the optimised anti- and gauche- structures based on HF/3-21G calculation method are shown below;

Conformer	Structure	Point Group	Energy/Hartrees	Energy/kcalmol^-1
anti		C_i	-231.69253528	-608303.5571
gauche		C₁	-231.69266121	-608303.8879

The point group of the anti-structure indicates that it has an inversion of symmetry, whilst the gauche-structure lacks symmetry.

The energies of the anti- and gauche- structures were calculated as -231.69253528 and -231.69266121 Hartrees with an energy difference of 0.3308 kJmol^-1, which indicates that the gauche conformation is in fact more stable; this is attributed to stereoelectronic effects in which there is an favourable interaction between the π orbital of the C=C bond and σ* orbital of the adjacent vinyl proton as shown belown in a Newman projection¹;

By comparing the structures I have optimised with those shown in Appendix 1, my structures correspond to anti2 and gauche3 conformers.

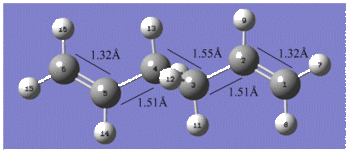
Reoptimisation of the C_i anti2 conformation of 1, 5-hexadiene at the B3LYP/6-31G* level resulted in an overall geometry change with very similar bond lengths but a siginicant increase in the outer dihedral angles by 4° as shown below. In terms of the energy, a final energy of -234.61170277 Hartrees was calculated which is in good agreement with the one given in the table for the anti2 conformer. The lowering of the energy compared to the energy calculated by the HF/3-21G method is due to the fact that the Hartree Fock method does not take into account electron distributions, which means that electronic effects such as CH-π interactions are not properly considered in the method².

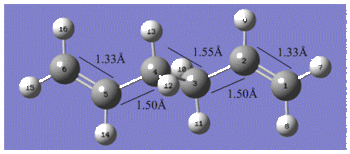The table below compares the bond angles of the C_i anti2 conformation for each method;

Calculation method	Torsional angle/°
Calculation method	C6-C5-C4-C3	C5-C4-C3-C2	C4-C3-C2-C1
HF/3-21G	114.7	-180.0	114.7
DFT/6-31G*	118.5	-180.0	-118.5

The outer dihedral angles are complements of each other which supports the C_i symmetry exhibited by the anti2 conformer

Frequency anaylsis confirmed that the optimium structure was a minimum as all the vibration frequencies were real and positive.

The table below shows the thermochemistry of anti2 conformer;

Thermochemistry	Energy
Sum of electronic and zero point energies/Hartrees i.e E = E_elec + ZPE	-234.469212
Sum of electronic and thermal energies at 298.15K and 1atm/Hartrees i.e E = E + E_vib + E_rot + E_trans	-234.461856
Sum of electronic and thermal enthalpies/Hartrees i.e H = E + RT	-234.460912
Sum of electronic and thermal free energies/Hartrees i.e G = H - TS	-234.500821

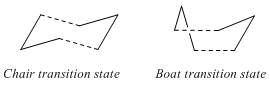
Optimizing the "Chair" and "Boat" Transition Structures

A transition structure optimisation was set up by i) computing the force constants at the beginning of the calculation, ii) using redundant coordinate editor and iii) using QST2. The reaction coordinate was also visualised and the IRC ran and the activation energies for the Cope rearrangement were calculated via the chair and boat transition structures.

The chair and transition structures for the Cope rearrangement shown in Appendix 2 both consist of two C₃H₅ allyl fragments positioned approximately 2.2 apart, one with C_2h symmetry and and the other with C_2v symmetry.

Chair Transition Structure

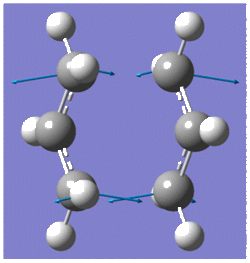
Firstly a suitable guess of the chair transition structure was constructed; an allyl fragment (CH₂CHCH₂) was drawn and then optimised using the HF/3-21G level of theory. The optimised allyl structure was then pasted twice into a new window so that the two fragments could be orientated into the chair conformer.

The chair transition structure optimisation was set up by both i and ii, where both methods used the HF/3-21G level of theory.

Optimisation to a TS(Berny)

This methods involves computing the force constant matrix (also known as the Hessian) in the first step of the optimisation which is then updated as the optimisation proceeds. The optimisation was set up so that the force constants were only calculated once with additional keywords, Opt=NoEigen, which prevents the calculation from crashing if more than one imaginary frequency is detected during the optimisation.

The frequency calculation gave an imaginary frequency of magnitude -817.96 cm^-1, which confirmed the transition state was optimised successfully.

Frozen coordinate method

In this method, the transition structure was generated by freezing the reaction coordinate, i.e the terminal carbons of each fragment which form/break a bond during rerrangement and then minimising the rest of the molecule using Opt=ModRedundant. Once the molecule was fully optimised, the reaction coordinate was unfrozen and optimisation to a transition structure was performed.

Comparison with the previous method give the same structure with a bond length between the terminal end of the allyl fragments as 2.02Å, suggesting that both methods are equally accurate. However, in some cases, if the guessed transition structure is not close enough to the correct structure, method i may fail as the curvature of the surface may be significantly different at points far removed from the transition structure. This would make the frozen cooodinate method more reliable as well as more time-efficient and less expensive as the whole Hessian may not need to be computed once this is done.

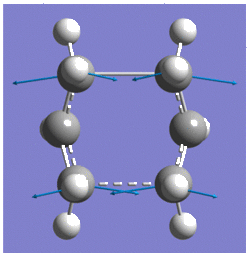
Boat Transition Structure

The boat transition structure optimisation was set up by QST2 method at the HF/3-21G level of theory, which involves specifying the reactants and products for the reaction and then calculating the interpolation between the two structures to find the transition state betweeen them. This meant the numbering for the product molecule had to be changed so that it corresponded to the numbering obtained in if the reactant had rearranged. However, the method failed to locate the boat transition structure; the top allyl fragment was simply translated without the possibility of accounting for the rotation around the central bonds.

Thus, the reactant and product geometries were modified so that the central dihedral C-C-C-C angle was changed to O° , whilst the central C-C-Cs were reduced to 100°. By using the same QST2 method, optimisation to a boat transition structure was successful, which was confirmed by frequency analysis; one imaginary freqency at -839.84cm^-1.

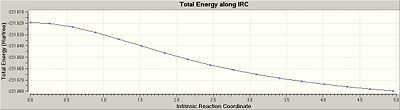
Intrinsic Reaction Coordinate (IRC)

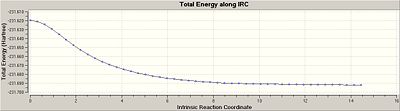
The IRC method allows you to follow the minimum energy path from a transition structure down to its local minimum as the product on a potential energy surface. This was set up by computing the reaction coordinate in the forward direction only as it is symmetrical and calculating the force constants once. Also 50 points were considered along the IRC.

An IRC calculation for the optimised chair transition structure gave 17 intermediate geomtries. Since the minimum had not been reached yet as indicated by the RMS gradient along the IRC not equalling to zero, the last point on the IRC was ran for a normal optimisation. This resulted in the a minimum structure corresponding to the gauche2 conformer with an energy of -231.691199702 Hartrees.

Re-running an IRC by specifying a larger number of points until a minimum was reached was not an option since the inital IRC calculated 17 intermediate geomtroes which is well within the number of points that was specified i.e 50. Therefore, in order to confirm a local minimum had been reached an IRC calculation was re-ran but with the force constants were computed at every step. As a result, 47 intermediate geometries were located with an IRC pathway reaching an asymptote and thus RMS gradient equalling to zero, which suggested that the local minimum had been reached. Nevertheless, the last point on IRC was ran for a normal optimisation and the local minimum was confirmed as gauche2with an energy of -231.69166700 Hartrees. Thus, the IRC method determined the Cope rearrangement of the anti2 conformation of 1, 5-hexadiene to give the gauche2 conformer.

Property	Endo TS	Exo TS
Structure from side
RMS gradient along IRC
Structure
Energy/Hartrees	-231.69166702	-23.69166700

Calculation Activation Energies

Re-optimisations of the chair and boat transition structures were performed using the B3LYP/6-31G* level of theory followed by frequency calculations to confirm the optimisations were successful, and then compared with the HF/3-21G method. Additionally, the activation energies were also calculated for the reaction via both transition structures. The results are tabulated below;

Method	HF/3-21G			B3LYP/6-31G*
	Electonic energy/Hartrees	Sum of electronic and zero point energies at OK/Hartrees	Sum of electronic and thermal energies energies at 298.15K/Hartrees	Electonic energy/Hartrees	Sum of electronic and zero point energies at OK/Hartrees	Sum of electronic and thermal energies energies at 298.15K/Hartrees
Chair TS	-231.619322	-231.466697	-231.461339	-234.556983	-234.414931	-234.409010
Boat TS	-231.602802	-231.450928	-231.445298	-234.543093	-234.402340	-234.396006
Reactant (anti2)	-231.692535	-231.539539	-231.532565	-234.611703	-234.469212	-234.461856

Summary of activation energies/kcalmol^-1

Method	HF/3-21G		B3LYP/6-31G*
	at OK	at 298.15K	at 0K	at 298.15K
ΔE (Chair TS)	45.70	44.69	34.06	33.16
ΔE (Boat TS)	55.60	54.76	41.96	41.32

At both levels of theory, the geomtries are reasonably similar, but energy differences between the reactant and the transition states are markedly different. By using B3LYP/6-31G* which is higher and more accurate level of theory, the energies of both transition states have decreased and the activation energies for both transition structures are in much better agreement with the experimental values of 33.5 ± 0.5 and 44.7 ± 2.0 kcalmol^-1. For both levels of theory, the results are also consistent with the Appendix 2.

Results show that the chair transition state is more stable than that of the boat with a lower activation energy of 33.16 kcalmol^-1 at compared to 41.32kcalmol^-1 at room temperature. Therefore, it can be concluded that the reaction mechanism of the Cope rearrangement prefers to proceed via the chair than the boat transition state.

References

Nishio. M, Hirota. M, (1989). Tetrahedron. 45: 7201
Rocque. B. G, Gonzales. J. M, Schaefer III. H. F, (2002). "An analysis of the conformers of 1,5-hexadiene" Molecular Physics. 100 (4): 441-446 DOI:10.1080/00268970110081412