mod 3

The Cope Rearrangement Tutorial

Optimizing the reactants and products

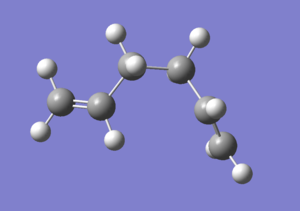
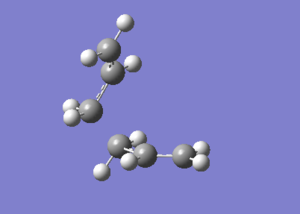
The "anti" and "gauche" conformation of 1,5-hexadiene is optimized at the HF/3-21G level of theory.

*Table 1* - the two conformers of 1,5-hexadiene optimized using HF/3-21G
Conformers	Structure	Energy/ a.u.	Energy / kJ mol^-1	Symmetry group
anti		-231.69253528	-608308.7506	C_i
gauche		-231.69153035	-608306.1128	C₂

The gauche conformation is expected to have a higher energy then the anti structure, as the eclipsing large groups are close to each other and results in steric clash which raises the energy. The calculation shows that the gauche conformation is indeed higher in energy by 2.64 kJ/mol.

Graph 1 - the structure of the gauche 1,5-hexadiene in Newman projection

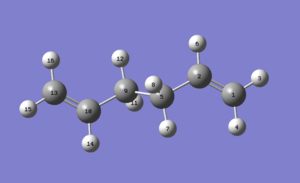
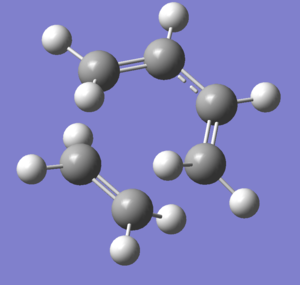
We can see that the structure in graph 1 can be further optimized by adjusting the positions of the two H2C=C groups to lower their steric clash. A new gauche conformer is drawn and optimized using HF/3-21G.

Graph 2 - Predicted lowest energy gauche conformation of 1,5-hexadiene

The energy after optimization for the structure in graph 2 is -231.69266120 a.u., which is -608309.082 kJ mol^-1. This is more stable than the structure in graph 2 by 2.97 kJ mol^-1. The point group of the new structure is C1.

Comparing the optimized structure with the structures in Appendix 1, the first optimized gauche structure (as shown in graph 2) corresponds to the gauche 2 structure. The second optimized gauche structure (as shown in graph 3 and 4) corresponds to the gauche 3 structure.

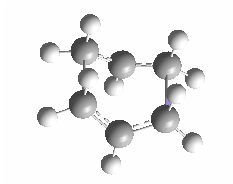
The Ci anti2 conformation of 1,5-hexadiene was optimized at HF/3-21G level of theory in the section above. It is now optimized again using DFT-B3LYP/6-31G(d) level of theory. The energies and geometries of the two structures are compared in table 2.

*Table 2* - comparison of the geometries and energies of anti2 conformation of 1,5-hexadiene optimized at HF/3-21G and DFT-B3LYP/6-31G(d)
Level of theory	HF/3-21G	DFT-B3LYP/6-31G(d)
Structure
C=C bond length/Å	1.32	1.33
C-C bond length/Å	1.51 (C2-C5 and C9-C10); 1.55 (C5-C9)	1.50 (C2-C5 and C9-C10 ), 1.55 (C5-C9)
C-H bond length/Å	1.07-1.09	1.09-1.10
C(2,5,9) and C(5,9,10) dihedral angle/°	111.3	112.7
C(1,2,5 and 9,10,13) dihedral angle/°	124.8	125.3
Energy/ a.u.	-231.69253528	-234.61170280
Energy/ kJ mol^-1	-608308.7506	-615973.026

Reoptimization of the anti2 conformation of 1,5-hexadiene at the DFT-B3LYP/6-31G(d) level of theory results in no major change in geometry. The bond lengths are very similar (however in general, the reoptimized structure has slightly longer bond lengths). The dihedral angles are all very similar as well, although in general, the reoptimized structure has slightly larger dihedral angles.

Vibrational frequency analysis

Frequency analysis shows that the optimized structure has no imaginary vibrations, only real ones. This conforms that the optimum structure was a minimum.

Graph 4 - the IR spectrum of C_i 'anti2 conformation of 1, 5-hexadiene

The thermochemistry of C_i 'anti2 conformation of 1, 5-hexadiene
Sum of electronic and zero-point energies/a.u.	-234.469212
Sum of electronic and thermal energies/a.u.	-234.461856
Sum of electronic and thermal enthalpies/a.u.	-234.460912
Sum of electronic and thermal Free Energies/a.u.	-234.500821

Optimizing the "chair" and "boat" transition structures

Optimizaing the chair transition structure

Firstly, an allyl fragment (CH₂CHCH₂) was drawn and optimized using the HF/3-21G level of theory. The optimized allyl fragment was pasted twice and oriented into a structure that mimics the chair transition structure .

Graph 5 - the orientation of two allyl fragments to mimic the chair transition structure

The transition state was then manually optimized using two methods. The first method is to use Hartree Fock and the default basis set 3-21G . The second method is the frozen coordinate method.

Using Hartree Fock and basis set 3-21G

Graph 6 - the structure of the transition structure optimized using Hartree Fock and basis set 3-21G

The distance between atom [1] and [2] is 2.20Å. Frequency calculation of the optimized structure gave an imaginary frequency of magnitude -817.97 cm^-1, which confirms that the transition state was successfully optimized. The movie for the vibration is recorded and can be accessed here.

Using the frozen coordinate method

The transition structure is optimized again using the frozen coordinate method. The distances between the two terminal carbons on both sides of the transition structure was 'frozen', and then optimized. After the first optimization, the four terminal carbons were 'unfrozen', and the structure was optimized again.

The final optimized structure is the same as the structure optimized using Hartree Fock and 3-21G in graph 6, with the distance between the terminal carbons of the two allyl fragments 2.02A. This suggests that both methods are equally accurate for the boat transition structure.

Optimizing the boat transition structure

The boat transition structure is optimized using the QST2 method, which specifies the reactants and products for a reaction in attempt to calculate the transition state. The DFT-B3LYP/6-31G(d) optmized anti2 1,5-hexadiene structure was duplicated, labelled and oriented so that they mimic the reactant and product. Then, the first QST2 calculation was run, but this job failed as the starting structures differed too much from the transition state. Therefore, the structure of the starting structures were modified so that they are closer to the boat transition state structure.

Graph 7 - the modified starting structures

The QST2 calculation was started again. This time, the transition state structure was successfully located.

Graph 8 - the boat transition state structure located using the QST2 method

The IRC calculation

Looking at this transition structure, as well as the structure for the chair transition state, it is impossible to predict which conformer will form. However, another method called the Intrinsic Coordinate (IRC) Method allows us to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface.

To find out the minimum energy path of the reaction, the IRC calculation was run for the chair transition state structure. However, after the calculation, the minimum geometry was not reached yet. The energy of the final structure is -231.68049221 a.u..

To continue minimizing in attempt to reach the minimum geometry, the last point on the IRC was taken to run a minimum minimization using the HF/3-21G level of theory.

Graph 9 - the final structure of the geometry optimization

The energy of this structure is -231.69166702 a.u., which is slightly lower than the starting structure. However, this is still not the minimum geometry.

Another attempt to obtain the minimimum geometry was to redo the IRC, specifying that force constants should be calculated at every step. After redoing the IRC, the geometry minimum was obtained.

Graph 10 - the final structure after redoing the IRC

The energy of this structure is -231.79116428 a.u.. The RMS gradient norm for the calculation is 0.00001145 a.u., which is less than 0.001 a.u., showing that the optimization is converged. The first approach was much faster than the second approach, but as the starting structure was not close to the minimum structure to begin with, it was not able to locate the minimum structure. The second approach was more time-consuming, but it successfully calculated the minimum structure.

Activation energies

In this section, the activation energies for the reaction via both transition structures were calculated. Firstly, the chair and boat transition structure were reoptimized using the B3LYP/6-31G* level of theory and frequency calculations were carried out.The structures and energies of the optimized structures are compared with the geometry optimized using HF/3-21G level of theory.

Table 4 - comparing the chair transition structure optimized at two different levels of theory
Level of theory	Structure	Energy/a.u.	Energy/ kJ mol^-1
HF/3-21G		-231.680492	-608277.132
B3LYP/6-31G*		-234.563120	-615845.472

The two structures are similar, but the energy optimized using B3LYP/6-31G* level of theory is 7730 kJ mol^-1 lower.

Table 5 - comparing the boat transition structure optimized at two different levels of theory
Level of theory	Structure	Energy/a.u.	Energy/ kJ mol^-1
HF/3-21G		-231.670907	-608251.966
B3LYP/6-31G*		-234.6634537	-616108.898

The two structures are similar, but the energy optimized using B3LYP/6-31G* level of theory is 7857 kJ mol^-1 lower.

The imaginary frequency of the reoptimized boat transition structure is -532 cm ^-1, while the imaginary frequency of the reoptimized chair structure is -567 cm^-1.

Table 6 - Summary of energies for the Ci (*anti 2*) reactant, chair and boat transition state
	HF/3-21G			B3LYP/6-31G*
	Electronic energy/a.u.	Sum of electronic and zero-point energies at 0K/a.u.	Sum of electronic and thermal energies at 298.15K/a.u.	Electronic energy/a.u.	Sum of electronic and zero-point energies at 0K/a.u.	Sum of electronic and thermal energies at 298.15K/a.u.
Chair Transition State	-231.680492	-231.527869	-231.522510	-234.563120	-234.421066	-234.415145
Boat Transition State	-231.670907	-231.519026	-231.510941	-234.663454	-234.522703	-234.516360
*Reactant (anti2)*	-231.592535	-231.599506	-231.752501	-234.611702	-234.49195	-234.461849

The Diels Alder cycloaddition

Optimization and MO analysis of cis butadiene

The optimization of cis butadiene is carried out using GaussView 5.0.9. The AM1 semi-empirical molecular orbital method was used for the calculation.

Table 7 - the optimization of cis butadiene
File type	.log
Calculation type	FOPT
Calculation method	RAM1
Basis Set	ZDO
Charge	0
Spin	Singlet
E(RAM1)/a.u.	0.04879719
RMS Gradient Norm/a.u.	0.00001745
Dipole moment/ Debye	0.0414
Job CPU time	6.0 s

We can see that the optimization is converged, as the final RMS gradient is less than 0.001.

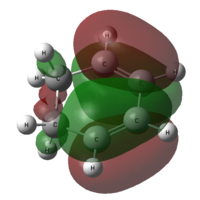
From the output checkpoint file of the optimization, we can visualize the molecular orbitals of cis butadiene. The HOMO and LUMO of the molecule are captured.

Table 8 - the HOMO and LUMO of *cis* butadiene
	HOMO	LUMO
cis butadiene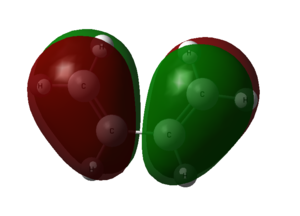
Symmetry with respect to molecular plane	Antisymmetric	Symmetric

Computation of the transition state geometry for the prototype reaction and an examination of the nature of the reaction path

Optimization of the transition state

In this section, the transition state geometry for the following reaction is studied. An initial guess of the transition state structure is drawn in GaussView and optimized in a three step process.

Graph 11 - the prototype reaction

Graph 12 - an initial guess of the transition state structure of the prototype reaction

The transition state structure proposed is first optimized using the freeze coordinate method. The distance between carbon atom 7 and 14, as well as 1 and 11, is fixed to 2.1Å using the redundant coord editor in GaussView. The AM1 semi-empirical molecular orbital method was used for the calculation.

Table 9 - optimization of the transition state structure using the freeze coordinate method
File type	.log
Calculation Type	FOPT
Calculation method	RAM1
Basis Set	ZDO
Charge	0
Spin	Singlet
E (RAM1)/a.u.	0.11123824
RMS Gradient Norm/ a.u.	0.00342233
Dipole Moment/ Debye	0.5749
Job CPU time	14 s

Graph 13 - the structure of the transition state after the first optimization

The structure is then reoptimized, which allows the bond distances that was previously frozen to be optimized. The optimization is to TS (berny), and used AM1 semi-empirical molecular orbital as the method.

Table 10 - optimization of the transition state structure after defrozing the reaction coordinates
File type	.log
Calculation Type	FTS
Calculation method	RAM1
Basis Set	ZDO
Charge	0
Spin	Singlet
E (RAM1)/a.u.	0.11165464
RMS Gradient Norm/ a.u.	0.00001482
Dipole Moment/ Debye	0.5608
Job CPU time	33 s

Comparing the calculation summary of the first and second optimization, we can see a significant decrease in RMS gradient norm. After the first optimization, the RMS gradient norm is larger than 0.001 a.u., indicating that the optimization is not yet converged. After the second optimization, the RMS gradient norm is well below 0.001 a.u..

Graph 14 - the structure of the transition state after the second optimization

After the second optimization, the transition state is optimized again, this time using a more accurate DFT/B3LYP/6-31G (d) level of theory. The frequency is also calculated.

Table 11 - optimization of the transition state structure using DFT/B3LYP/6-31G (d) level of theory
File type	.log
Calculation Type	FREQ
Calculation method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
E (RB3LYP)/a.u.	-234.54389655
RMS Gradient Norm/ a.u.	0.00000806
Dipole Moment/ Debye	0.3940
Job CPU time	6 minutes 48 seconds

Graph 15 - the labelled structure of the transition state after the third optimization

The structure of the final optimized structure is analyzed and summarized in the table below.

Table 12 - Final optimized transition state structure
C7 and C14, C1 and C11 bond distance/Å	2.27
C2 and C5 bond distance/Å	1.41
C1 and C2, C5 and C7 bond distance/Å	1.38
C11 and C14 bond distance/Å	1.39
C1,C2,C5,C7 dihedral angle/°	0.0
C1,C2,C5 and C2,C5,C7 angle/°	122.0

The imaginary frequency after the third optimization is -525 cm^-1. The imaginary frequency is expected from a transition state. Animation of the vibration at -525 cm^-1 shows that it corresponds to synchronous bond formation.

Molecular Orbitals of the Transition State Structure

Table 13 - the HOMO and LUMO of the transition state structure
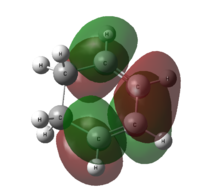
Molecular orbitals	HOMO	LUMO
Transition state
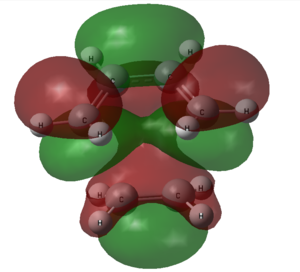
Symmetry with respect to molecular plane	Symmetric	Symmetric

Comparing the shapes of the LUMO and HOMO with the HOMO and LUMO of cis butadiene and ethylene in table ? above, it can be seen that the LUMO is formed from ethylene HOMO orbital and butadiene LUMO orbital. The HOMO is formed from ethylene HOMO and butadiene LUMO. These orbitals are allowed to interact because they have the same symmetry.

Studying the regioselectivity of the Diels Alder Reaction

In this section, the Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride is studied.

Graph 16 - the Diels Alder reaction between Cyclohexa-1,3-diene and Maleic Anhydride

Two products are formed in the reaction. It is well known that the kinetic product, which is the endo product, is predominantly formed. The reaction is supposed to be kinetically controlled, with the exo transition state higher in energy.

The transition state for both the endo and the exo product was located. Their structures were optimized, and energy compared. The final geometry of the structures was also measured. The molecular molecules, especially the HOMO and LUMO, for the transition states were calculated using GaussView 5.0.9.

Optimizing the reactants

The reactants for this reaction, cyclohexa-1,3-diene and maleic anhydride is optimized using the semi-empirical AM1 method. The HOMOs and LUMOs are sketched.

Table 14 -The HOMOs and LUMOs of cyclohexa-1,3-diene and maleic anhydride
	cyclohexa-1,3-diene		maleic anhydride
Molecular Orbitals	HOMO	LUMO	HOMO	LUMO
Sketches
Symmetry	Antisymmetric	Symmetric	Symmetric	Antisymmetric
Energy of the optimized molecule/a.u.	0.02771129		-0.12182423

Sketching the MOs of the reactants allows us to analyze the MOs of the transition state later and to determine which orbitals will be interacting to form the product.

Optimizing the exo transition state

The exo transition state was sketched in GaussView and optimized in a three-step process: firstly the distance between the reaction coordinates were freeze to 2.2Å using the Redundant Coord Editior and optimized to minimum using semi-empirical AM1 calculation method. After the first optimization, the reaction coordinates were unfrozen and optimized again to TS (berny) using semi-empirical AM1 calculation method. After this, the structure was optimized the third time to TS(berny) using a more accurate DFT-B3LYP/6-31G(d) level of theory. The frequency was also calculated when carrying out the third optimization.

Table 17 - Summary of calculation after each optimization
	Freeze coordinate (semi-empirical AM1)	Unfreeze coordinate (semi-empirical AM1)	Unfreeze coordinate (DFT-B3LYP/6-31G(d))
Structure
File type	.log	.log	.log
Calculation type	FOPT	FREQ	FREQ
Calculation method	RAM 1	RAM 1	RB3LYP
Basis set	ZDO	ZDO	6-31G(d)
Charge	0	0	0
Spin	Singlet	Singlet	Singlet
Energy/ a.u.	-0.05433384	-0.05041984	-612.67931095
RMS Gradient Norm/ a.u.	0.00683174	0.00000499	0.00001134
Dipole moment/ Debye	5.9268	5.5640	5.5496
Job CPU time	27 seconds	3 seconds	31 minutes 8 seconds
Distance between the reaction coordinates/Å	2.20	2.17	2.20
Imaginary frequency/ cm^-1	-	-812	-448

File for the final optimization can be found at DOI:10042/to-10181

After the second optimization, the distance between the reaction coordinates is 2.17Å. After the third optimization, the distance between the reaction coordinates is 2.20Å. The RMS Gradient Norm for the last optimization is less than 0.001, which proves that the optimization is converged.

After the optimization, the geometry of the optimized structure is analyzed.

Graph 17 - the labelled diagram of the exo transition state after optimization

Table ? - Geometry analysis of the optimized *exo* transition state
Bonds	Bond lengths/ Å
C1 and C3, C6 and C5	1.39
C5 and C13	1.39
C3 and C6	1.40
C1 and C8, C10 and C15	1.51
C8 and C10	1.56
C13 and C17, C5 and C18	1.50
C18 and O19, C17 and O19	1.40
C18 and O21, C17 and O20	1.20

The HOMO and LUMO of the optimized exo transition state is calculated using GaussView.

Table 18 - The HOMO and LUMO of the optimized *exo* transition state
	HOMO	LUMO
Structure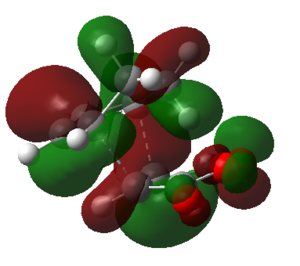
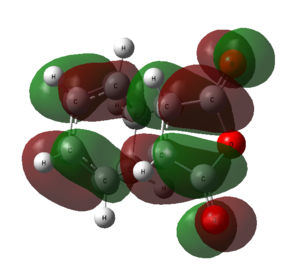
Symmetry	Symmetric	Antisymmetric

The HOMO of the exo transition state is formed from the LUMO of cyclohexa-1,3-diene and HOMO of maleic anhydride. The LUMO of the transition state is formed from the HOMO of cyclohexa-1,3-diene and LUMO of maleic anhydride.

Optimizing the endo transition state

Same as optimizing the exo transition state, the endo transition state is optimized in a similar 3-step process: first, freeze the distance between the reaction coordinates to 2.2Å using the Redundant Coord Editior and optimized to minimum using semi-empirical AM1 calculation method. This is followed by unfreezing the and optimized again to TS (berny) using semi-empirical AM1 calculation method. After this, the structure was optimized the third time to TS(berny) using a more accurate DFT-B3LYP/6-31G(d) level of theory. The imaginary frequency was also calculated when carrying out the third optimization.

Table 19 - Summary of calculation after each optimization
	Freeze coordinate (semi-empirical AM1)	Unfreeze coordinate (semi-empirical AM1)	Unfreeze coordinate (DFT-B3LYP/6-31G(d))
Structure
File type	.log	.log	.log
Calculation type	FOPT	FREQ	FREQ
Calculation method	RAM 1	RAM 1	RB3LYP
Basis set	ZDO	ZDO	6-31G(d)
Charge	0	0	0
Spin	Singlet	Singlet	Singlet
Energy/ a.u.	-0.05238788	-0.0515048	-612.68339675
RMS Gradient Norm/ a.u.	0.00272262	0.00000811	0.00000704
Dipole moment/ Debye	6.0005	6.1660	6.1142
Job CPU time	16 seconds	3 seconds	35 minutes 32 seconds
Distance between the reaction coordinates/Å	2.20	2.16	2.27
Imaginary frequency/ cm^-1	-	-806	-447

After the optimization, the geometry of the optimized structure is analyzed.

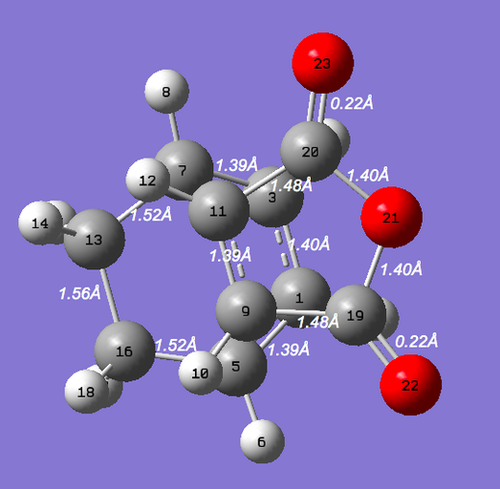
Diagram 17 - the labelled diagram of the endo transition state after optimization

Table 19 - Geometry analysis of the optimized *endo* transition state
Bonds	Bond lengths/ Å
C1 and C5, C3 and C7	1.39
C1 and C3	1.40
C5 and C16, C13 and C7	1.52
C1 and C8, C10 and C15	1.51
C13 and C16	1.56
C11 and C20, C9 and C19	1.48
C20 and O21, C19 and O21	1.40
C19 and O22, C20 and O13	0.22

The HOMO and LUMO of the optimized endo transition state was calculated using GaussView.

Table 19 - The HOMO and LUMO of the optimized *exo* transition state
	HOMO	LUMO
Structure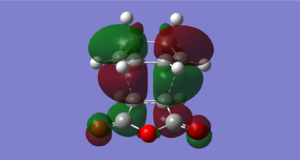
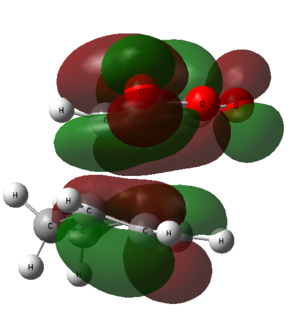
Symmetry	Antisymmetric	Antisymmetric

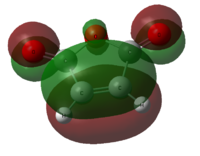
Secondary orbital overlap effect

Experimental observation is that the reaction between maleic anhydride and cyclopentadiene gives the endo adduct faster than they give the exo adduct even though the latter is more thermodynamically stable.(pp.106). This is because the transition state of the endo isomer is lower in energy, as show in the table below:

Table 20 - The energies of the optimized transition states from the DFT-B3LYP/6-31G(d) optimization
	Exo adduct	Endo adduct
Energy/a.u.	-612.67931095	-612.68339675
Energy/kJ mol^-1	-1608589.5309	-1608600.2582

The exo adduct is more stable than the endo adduct by 10.7 kJ mol^-1. This is due to the presence of secondary overlap of frontier orbitals in the endo transition state, which is not present in the exo transition state.

Diagram 18 - the interaction of frontier orbitals in the endo transition state

The dashed lines in the diagram above denote bond-forming interactions, while the dotted lines donate non-bond forming secondary orbital interactions. In the endo transition state, only bond-forming interactions are present:

Diagram 19 - the interaction of frontier orbitals in the exo transition state

The HOMO of both endo and exo transition states have nodal planes. However, secondary overlap is hard to confirm from the calculated HOMO diagrams, as they all show a similar degree of overlap. This might be due to the choose of method and basis set which is not accurate enough to be able to illustrate the secondary interactions in the calculated diagram. Hence, another more accurate method should be used to examine the HOMOs of the two transition states.

Examine the shapes of the optimized endo and exo transition states, we can see that for the exo isomer, the maleic anhydride molecule fragment is on the same side as the CH₂-CH₂ group. This leads to large steric strain in the transition state. For the endo isomer, the maleic anhydride fragment is on the opposite side as the CH₂-CH₂ group, which avoids the steric strain.

Therefore, the relative energy of the transition states is depend on two factors: the extent of secondary interactions between the frontier orbitals, and the extent of steric strain. The fact that the exo adduct is more stable shows that the stabilizing effect by the secondary interactions is greater than the destabilizing effect by the steric hindrance.

Rep:Mod3:YJY1234