Rep:Mod3:SquirrelSouffle
Module 3
Introduction
Multiple theories and models can be used to predict the reactivity of a system, by looking at the internal energies of molecules, and assuming that if it's stable it can exist. However, reactants do not just fall apart and recombine to make the product; they go through different stages of bonding, to reach the product. These half-way points are 'activated' complexes, and are known as transition states of the reaction. The transition state can be thought of a barrier, over which the reactants must pass, to form the products. In other words, the reactants need enough energy to form the transition state, which then forms the product. This required energy is known as the activation energy. The transition state has a different geometry, energy and different bonds when compared to either the product or reactants, due to changes in electron density, and this is unstable and unfavourable, causing the energy barrier.
Models which look solely at the starting and final energies of the system are unable to be used to analyse these transition state molecules, and as such we will be using a different model to the last two modules. Molcular mechanics has it's limitations in transition state studeis, due to the inability for it to understand the breaking or formation of bonds, nor the movement of electronic distribution. Due to the electronic nature of bonding, to be able to understand the movement of charge, or formation of bonds, we need a more quantum mechanical view of the system. These quantum mechanical models use the Schrodinger equation, and the analysis of the molecular orbitals of the system, to calculate energies and electronic movement, allowing to accurately calculate the transition state structures.
The Cope Rearrangement
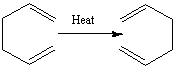
A Cope rearrangement is the name given to the [3,3]-sigmatropic rearrangement of 1,5-dienes, and in this study, we'll look at the specific Cope rearrangement of 1,5-hexadiene. The reaction follows a concerted mechanism, with the transition state taking on a chair or boat geometry. As with the chair and boat conformations of cyclohexane, the boat transition state is the transition state of highest energy, and so we would expect to see the reaction pathway take place through the chair transition state. The aim of this study is to look at the energy minima of the reaction, to find the transition state, and therefore the reaction mechanism.
Optimisation
To be able to accurately find the transition state, we need to know that our reactants are in their most stable form (i.e. the conformation in which they're most likely to react, to give the desired product). 1,5-hexadiene has multiple conformations, and the first stage is to find the most stable. The conformations can initially be split into two types: those with the central C3-C4 bond rotated so that the substituent carbon atoms are anti-periplanar, and those with the central C3-C4 bond rotated so that the substituent carbon atoms are gauche to each other. Each of the suggested conformations were modelled, and their data is below.

Following the supplied script, I started by looking for "anti 1". A molecule of 1,5-hexadiene was created in Gaussview by combining CH4 fragments, adding two double bonds in the 1 & 5 positions, and correcting the valencies. Being in the anti position, the dihedral angle between atoms C(2)-C(3)-C(4)-C(5) is 180o, and was made so using the available dihedral angle tool. The C(1)-C(2)-C(3)-C(4) and C(3)-C(4)-C(5)-C(6) dihedral angles were altered to a rough approximation of the expected geometry. The molecule was then 'cleaned', before optimisation via Gaussian, using the Hartree Fock method and 3-21G basis set. The calculations were run on the supplied departmental laptop, and took very little time. On the left, you can see the geometry minimized molecule of anti 1. Using the symmetrisation tool, Gaussview predicted the structure to belong to the C2 point group.
| Charge | 0 |
| Spin | Singlet |
| Dihedral Angle (o) | 176.9 |
| Final Energy (a.u.) | -231.6926 |
| RMS Gradient (a.u) | 0.000009 |
| Dipole Moment (D) | 0.02003 |
| Point Group | C2 |
To make an initial comparison of the gauche and anti conformations, the next molecule I aimed to construct was "gauche 1". The previous anti 1 structure was saved, and a copy was used to run these calculations. Being in the gauche conformation, the C(2)-C(3)-C(4)-C(5) dihedral angle needed to be 60o, which was again obtained using the dihedral angle tool in Gaussview. The dihedral angles of the other carbon-carbon bonds were altered as before, and the molecule was then cleaned before the Gaussian calculations. As with the previous molecule, the calculations were run using Hartree-Fock and the 3-21G basis set, to allow us to be able to compare the calculated results. When the total energy of the molecule was compared to the value given to us in the supplied appendix, gauche 1 had indeed been made.
As you can see from the data to the right, the anti periplanar conformation has the lower energy as we would expect. The energy of anti 1 is 12kJ/mol less than gauche 1, as the 180o dihedral angle means that the substituents are as far away from each other as possible, reducing any unfavourable destabilising (i.e. energy increasing) interactions. For the gauche conformer, the dihedral angle was minimised to 75.8o, and at this angle, there are bound to be multiple destabilising sterics. The anti periplanar dihedral angle was optimised to 176.9o, obviously avoiding the same destabilisation that the gauche conformer encountered.
However, steric factors are not the only variable that alters internal energy. A stabilising factor within molecules is the extent of conjugation of the bonds. The more conjugated the molecule, the more stable it becomes. In many cases, a conformation which is stabilised by the lack of steric hindrance, is not stabilised by the other factors. As such, a compromise is usually made in the most stable conformation, where the total stabilisation is greater than the total destabilisation. For our molecule of 1,5-hexadiene, the most stable conformation (as found initially by minimizing the energy without altering any dihedral angles) is one of these compromised molecules, where the dihedral angle over the central C-C bond is between the gauche and anti-periplanar conformations.
| Charge | 0 |
| Spin | Singlet |
| Dihedral Angle (o) | 67.7 |
| Final Energy (a.u.) | -231.6927 |
| RMS Gradient (a.u) | 0.00001 |
| Dipole Moment (D) | 0.03269 |
| Point Group | C1 |
| Charge | 0 |
| Spin | Singlet |
| Dihedral Angle (o) | 75.8 |
| Final Energy (a.u.) | -231.6877 |
| RMS Gradient (a.u) | 0.00001 |
| Dipole Moment (D) | 0.00466 |
| Point Group | C2 |
There are other conformations available of this molecule, such as eclipsed (syn-periplanar) and anti-clinal, as these conformers are of no use in this case, as they will undoubtedly have higher sterics than either the gauche or anti-periplanar conformations, with none of the stabilising interactions.
To check this, the central dihedral angle was now altered to 67.5o (as it is between the gauche angle, and the angle for gauche 1 (75.8o)), leaving the substituent atoms in their current positions. As with previous optimisations, this molecule was cleaned and then optimised using HF and the 3-21G basis set. The resulting structure was gauche 3 in the supplied appendix. This molecule was symmetrised, and as we would have expected, the point group has now been reduced to C1. When the calculated data from this molecule is compared to the previously most stable conformation (anti 1), we can see that indeed, the gauche 3 conformer is the most stable, with an optimised dihedral angle of 67.7o.
The gauche 3 conformation has a dihedral angle close to that of idealised gauche molecules, meaning that there must be large and unfavourable steric interactions. For this molecule to be the most stable, there must therefore be a stabilising force acting on the molecule, with a magnitude much greater than that for the destabilising sterics. I expect the stabilising force is due to the aforementioned conjugation of bonds, and more specifically, hyperconjugation of the orbitals, utilising the π electrons from the double bonds.
Basis Sets
| Charge | 0 |
| Spin | Singlet |
| Dihedral Angle (o) | 180.0 |
| Final Energy (a.u.) | -234.61171 |
| RMS Gradient (a.u) | 0.00001 |
| Dipole Moment (D) | 0.0000 |
| Point Group | Ci |
| Charge | 0 |
| Spin | Singlet |
| Dihedral Angle (o) | 180.0 |
| Final Energy (a.u.) | -231.69253 |
| RMS Gradient (a.u) | 0.000009 |
| Dipole Moment (D) | 0.0000 |
| Point Group | Ci |
A basis set is the name given to a set of equations, functions and approximations that are placed on a molecule, when a calculation is run. A smaller basis set is one that contains fewer functions/equations and more assumptions, making the calculations quick but not necessarily accurate. These small basis sets are okay to use on smaller molecules, due to the lower number of calculations actually carried out. Larger basis sets involve larger, more complicated equations and fewer assumptions, giving an accurate result, but at the cost of a long processor time.
So far, the calculations have been run using the 3-21G basis set, a very popular set, due to its fast processing time and relative accuracy when using simple atom types. The method used with this basis set was Hartree-Fock (HF), which is a simple quantum mechanical (QM) method used and is used primarily for the determination of the ground-state properties of the molecule. However, there are some large assumptions made within this method, such as the omission of any electronic correlation, which can cause a large deviation from experimental results. As such, molecule anti 2 was optimised using the HF/3-21G system, and then with a new system - DFT-B3LYP/6-31G*. The new method is a hybrid, using aspects of the HF method, supplemented by other functions, and is reliable, without much of an increase in processor time.
| HF/3-21G | DFT-B3LYP/6-31G | Literature[1] | |
| C=C Bond Length (Å) | 1.316 | 1.334 | 1.340 |
| CH2-CH Bond Length (Å) | 1.509 | 1.504 | 1.508 |
| CH2-CH2 (Å) | 1.553 | 1.548 | 1.538 |
| CH2-CH2-CH Bond Angle (o) | 111.3 | 112.7 | 111.5 |
| CH2-CH=CH2 Bond Angle (o) | 124.8 | 125.3 | 124.5 |
As expected, the change in method and basis set, has altered the calculated values of the properties of the anti 2 conformer. Only a simple comparison can be drawn as the references for the energies can be different, and because of fewer assumptions in the larger basis set. However, that being said, the dihedral angle and geometry of the molecule seem to be identical for both sets of calculations, though bond lengths have changed. As you can see in the table on the right, the bond lengths from both calculations are similar to the literature (experimental) values, and in some cases the results from the HF method are actually closer to the experimental values. However, as the second set of calculations are formed from a larger basis set and method, we should assume these results to be more accurate, and use them for any further calculations.
Vibrational Analysis
The previously optimised molecule of anti 2 (DFT-B3LYP/6-31G* optimised) was then run through Gaussian as a vibrational job. On the right you can see the energies of the molecule, that are kept in the log file when the job is processed.
| Sum of Electronic and Zero-Point Energies | -234.469195 |
| Sum of Electronic and Thermal Energies | -234.461847 |
| Sum of Electronic and Thermal Enthalpies | -234.460903 |
| Sum of Electronic and Thermal Free Energies | -234.500793 |
The vibrational data was then displayed in Gaussview. All of the vibrational frequencies are positive, meaning that the optimisations were successful and the ground state of the molecule has indeed been found. As seen later, negative frequencies are indicative of the structure not being the ground state, but that doesn't mean that the data is useless. Lots of vibrational frequencies were gathered for the molecule (over 40), and so displaying all of them here would be a waste of time. Vibrational frequencies are obtained for all the vibrations, but that does not mean that the vibrations are going to be visible when an infra-red spectrum is taken. For the vibration to be infra-red active, there needs to be a change in total dipole of the molecule, during the vibration. The molecule here has a centre of inversion, and as such, we would not expect to see all vibrations in the spectrum, as many of the vibrations occur through the centre of inversion. This means there are (at least) two separate dipole changes in the molecule, but they are equal and opposite, giving no overall change. We actually see that 21 of the vibrations have no intensity at all, whilst a few have negligible intensities.
Transition State Structure
As we now know the most stable conformation of the reactant, the next stage is to look at the transition state. As stated above, the 6-membered, cyclic transition state can either be in the boat conformation or the chair conformations. In this stage of the analysis, we will highlight three major routes for the determination of transition states. We will also look at a method that can visualise the formation of the transition state, known as the Intrinsic Reaction Coordinate (IRC).
Optimisation of Boat & Chair Transition States
 |
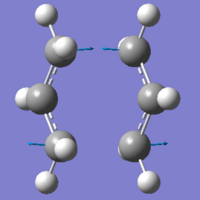
An allyl fragment was created in Gaussview, cleaned and then optimised to a minimum energy, using the previous HF/3-21G method as before. This optimised form was then saved, duplicated, and then rotated, as to have the two identical allyl groups in a possible chair transition state geometry. As per the instructions, the distance between the two planar fragments was made to be as close to 2.2Å as possible, measured between the pairs of terminal carbon atoms. This system was then run through Gaussian using an Opt+Vib job, allowing us to decrease calculation time, by using the data from the optimisation in the vibrational calculations, automatically. The system was not optimised to a minimum as the fragments were, as the minimum is always going to be a stable structure, but we want the transition state - an unstable, high-energy conformation. As such, the job was set to optimise the system into a transition state, using the method TS(Berny), with the HF/3-21G parameters.
As mentioned briefly before, negative frequencies in a vibrational analysis mean you have not found the true ground state. However, if you find just one negative/imaginary frequency, then you actually have found a transition state. Any more than one imaginary vibration however, and you have neither a transition state nor ground state. Gaussian is programmed to stop the calculations if negative frequencies are found, and so to stop this from happening, we can add the optional parameter "opt=NoEigen", which forces the software to continue the job if negative frequencies of vibration are found. Another variable in the job menu is the calculation of force constants. As with mechanical springs, the bonds vibrate and move in a range permitted by a force constant. In these jobs, we are able to alter when these force constants are calculated. We can calculate the constants at every stage, giving an accurate representation of the system, at a loss of using more processing time. The other options are that we can not calculate them at all, or we just calculate the constants once, under the assumption that there will be very little change in the constants throughout the calculations. For this job, we ran the force calculations once, at the start of the job, and as such this method is called the 'force constant' method. The procedure yielded an arrangement of the molecules that by eye, looked no different to the starting arrangement.
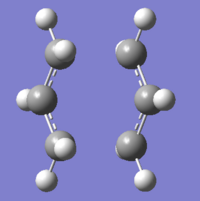
The second method that can be used in the calculation of transition states is know as the 'redundant coordinate' method. For this, the original optimised form of the two fragments was used, and the two terminal pairs of carbon atoms were 'frozen' with a bond length of 2.2Å, so in the upcoming optimisations, the bond length would stay fixed. When the opt+freq job was run as above, there was a new line in the job type; "opt=modredundant". When the job was finished, the resulting molecule was then altered again with the "redundant coordinate editor", setting the previously 'frozen' bonds to 'derivative'. This molecule was then optimised, and it's frequencies of vibration calculated again, with the same method and basis set as before, giving another molecule - the transition state structure as calculated by the redundant coordinate method.
| Force Constant | Redundant Coordinate | |
| C-C-C bond angle within allyl fragments (o) | 120.5 | 120.5 |
| Distance between planes of the molecules (Å) | 1.39 | 1.39 |
| C-C bond length within allyl fragments (Å) | 2.02 | 2.02 |
| Total Energy (a.u.) | -231.6193 | -231.6152 |
| RMS Gradient (a.u.) | 0.00004 | 0.0004 |
| Spin | Singlet | Singlet |
| Charge | 0 | 0 |
| Dipole (D) | 0.0000 | 0.0000 |
| Point Group | C2h | C2h |
| Frequency of Imaginary Vibration (cm-1) | -818 | -818 |
As you can see from the table above, the values calculated by the two different methods are very similar when it comes to the geometry of the molecule. The differences just seem to be in the total energies, and the RMS gradient. From the vibrational data, we can see we've got two similar frequency imaginary vibrations, which actually represent the movement of the atoms, in the formation of the transition states.
 |
 |
 |
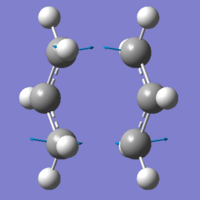 |
Although in this case, the data is very close and geometry very similar, in some cases there is a big change when different methods are used. Here, we know the basics of how the two planar molecules can approach and form a transition states, but for some theoretical or new reaction, we may not be so sure. The first method, with the force constant is a method that is only reliable when we know the reaction pathway, and have the molecule optimised to a geometry very similar to the transition state. If our molecules are too far from the transition state, the calculations will fail, and no transition state is found. The second method, using the redundant coordinates is more useful than the force constant method as it follows the expected pathway, found when atoms are "frozen", lowering computational time.
The third and final method does not use TS(Berny) as in the previous calculations, but QST2 instead. This method uses the coordinates of your product and reactants, and then can calculate the possible methods of arriving from the reactants to the products, and follows the most likely pathway to the transition state. Here, we are looking at the boat conformation of the transition state. Using a previously optimised molecule of anti 2, two separate molecules of anti 2 were created within a Gaussview mol group.

The window view was split, and then both molecules were viewed side-by-side. To be able to successfully calculate the boat transition state, we need the two molecules to be in conformations that we would expect the product and reactant to be in. The QST2 method uses the internal atom labelling system to calculate the movement of atoms from product to reactant, so using the atom coordinate table, I was able to re-label the atoms, so that the product and reactant molecules were labelled correctly. If the atoms weren't labelled, Gaussian would have a problem trying to calculate a transition state, and would likely not produce any results.
Using these correctly labelled molecules, a Gaussian Opt+Freq job was run, optimising to "TS(QST2)", using the HF/3-21G system. It produced a molecule, that, unlike the previous methods, was able to draw in the bond being made in the transition state, which helped with understanding the process.
By looking at the table created in the vibrational analysis, we could see that there was only one imaginary vibration, and so we know that a transition state was obtained.The imaginary vibration here relates to the breaking and formation of the bonds in the Cope rearrangement. By comparing total energy values of the 2 possible transition state conformations, we can see that the energy corresponding to the chair transition state is much lower that that for the boat, as was originally hypothesised. This leads me to believe that the transition state geometry for the Cope rearrangement of 1,5-hexadiene, is the chair conformation, as it would mean a lower energy barrier for the reaction, than the boat conformation.
Intrinsic Reaction Coordinate (IRC)
The Intrinsic Reaction Coordinate is a method that allows the formation of computational transition states, by following the minimum of the reaction pathway between the transition state and the minimum on the potential energy surface of the product, or reactants. This method can be applied to find which conformation of reactants is more likely to produce a specific transition state, and vice versa.
For the calculated chair transition state, an IRC Gaussian job was run. Being symmetrical, the calculation direction could be either backwards or forwards, so forwards was chosen for simplicities sake. The number of points over which the pathway was calculated, was set to N=50, and the force constants were set to only be calculated at the start of the calculations. To be able to compare results to the previous calculated data, the same HF/3-21G parameters were used. As mentioned in the script, the resulting molecule has not yet reached its minimum geometry. From here, there was a choice as to how the calculations should progress, and there were three options. The first option is to have optimised the final structure of the last point of the IRC. This route is quick and easy, but may not follow the same pathway as the original IRC, and can end up finding another, unintended minimum. The second option is to run the IRC from the beginning, but with a larger number of points to be calculated i.e. more than 50. This route is much more reliable than the first option, but with so many points being calculated, Gaussian may continue past the minimum you want, and find another minimum instead. The third and final option is to run another IRC from the beginning, but this time instead of calculating the force constants once, and at the start of the calculations, the force constants can be calculated after every change in geometry. This final method is the most accurate, however it is also the most computationally powerful job, and so is limited to small molecules.
I chose to start the IRC calculations again, but with calculating the force constants at every point. This is because the molecule is relatively simple, and the SCAN cluster of computers was available. According to the log file produced, the final energy of the potential energy surface reached from the transition state is -231.6916 Hartrees, very similar to the -231.6917 Hartrees of the gauche 2 molecule, confirming that the gauche 2 molecule forms the chair transition state.
| HF/3-21G | B3LYP/6-31G* | |||
|---|---|---|---|---|
| Electronic energy (a.u.) | Sum of electronic and zero-point energies (a.u.) | Electronic energy (a.u.) | Sum of electronic and zero-point energies (a.u.) | |
| at 0 K | at 0 K | |||
| Chair TS | -231.619320 | -231.466701 | -234.556983 | -234.414936 |
| Boat TS | -231.602802 | -231.450928 | -234.543093 | -234.402338 |
| Reactant (anti 2) | -231.692535 | -231.539539 | -234.611715 | -234.469195 |
We can tell that the chair transition state is the most stable, and therefore most likely to be the actual geometry, but to be sure, we need to compare the activation energies for both of the possible transition state structures. To do this, the 'sum of electronic and zero-point energies' for the anti 2 conformer was subtracted from the 'sum of electronic and zero-point energies' for each transition state. For a reasonable comparison to other activation energies, the resulting value in Hartrees, is converted to kcal/mol using the conversion factor of 627.509kcal/mol per Hartree. As I only have the data for at 0K, the activation energies will only be for at 0K.
| HF/3-21G | B3LYP/6-31G* | Experimental | |
| at 0 K | at 0 K | at 0 K | |
| ΔE (Chair)(kcal/mol) | 45.71 | 34.05 | 33.5±0.5 |
| ΔE (Boat)(kcal/mol) | 55.60 | 41.95 | 44.7±2.0 |
The two tables above show that although the three molecules in question have similar geometries, the difference in energies is relatively large. This shows why we use low-level basis sets and calculation methods, so we can get a basic view of the potential nergy surface, and then a higher set of calculations are run, to optimise the molecule close to the surface.
The Diels-Alder Reaction
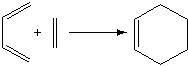
The Diels Alder reaction is the classic example of a [4+2] cycloaddition. The reaction consists of a diene and a dienophile undergoing a concerted pericyclic reaction, and it therefore has no intermediates - ideal for a transition state study. A Diels-Alder reaction is easy to explain, just by looking at the molecular orbitals involved. The HOMO of the diene and the LUMO of the dienophile are where we have the strongest orbital interactions, and so these are the molecular orbitals we expect to be primarily involved in this reaction. The interactions are strong due to having similar energy values. For a Diels-Alder reaction, if the difference in interacting HOMO and LUMO energy is too great, there is not enough "push" to complete the reaction in a concerted fashion, and it becomes stepwise. A step-wise Diels-Alder reaction cannot exist, and so we see no reaction occurring. Substituents on the diene and dienophile can greatly alter the energy of the orbitals involved, allowing for some interesting reactions. However, in this case we are looking at the simplest possible Diels-Alder reaction - the reaction between ethene and cis-butadiene.
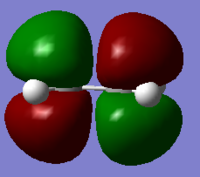
Both the ethylene and cis-butadiene molecules were created in Gaussview, and optimised to an energy minimum using the semi-empirical AM1 method, along with the 3-21G basis set as before. AM1 is also based upon the original HF method, and includes many factors left out of the HF method. Looking at the molecular orbitals below, we can clearly see the symmetry of the HOMOs and LUMOs, allowing us to predict orbital interactions. Symmetrical orbitals can interact well with other symmetrical orbitals, and anti-symmetric orbitals interact best with other anti-symmetric orbitals. Therefore, we can say that either the LUMO of the diene interacts with the HOMO of the dienophile, or the HOMO of the diene interacts with the LUMO of the dienophile, as already stated, as the two HOMOs and two LUMOs are unable to interact with themselves.
The transition state structure for this simplified reaction adopts an 'envelope' geometry, to maximise the stabilising overlap between the ethylene π orbitals and the π system of the cis-butadiene. As with all of the previous methods, we've tried to find out transition state by making a system that's very similar to the transition state in question, so the software cannot choose another minimum, and we reduce the number of calculations. Here, we can choose to try and model the transition state from the reactants, or from the product. Gaussview is a useful tool for calculations, but for the placement of atoms within its workspace, it is limited. As such, the easiest route to make our product is to start with a molecule that has the correct conformation, and then to remove and edit parts as required. The cyclohexene is in the boat/envelope shape, and this is not an energy minimum, so minimising the energy of our product, for transition state calculations, posed a slight problem. However, the software can easily optimise the structure in the first set of transition state calculations, so the effect is negligible.
The product molecule was split into fragments used to represent the two reactants, and the distance between the two fragments was set to 2.2Å, as this was a distance previously used, earlier in the module. This molecule then had an opt+freq Gaussian job run on it, using AM1/3-21G, and optimising to a TS(Berny). As we were expecting a transition state, "opt=NoEigen" was added to the parameters, to stop the calculations from failing once it found an imaginary frequency.
A new molecule was obtained, with two new sigma bonds that were absent in the reactants. The C-C bond lengths were both 2.119Å which are larger than I expected, but are still likely considering how these bonds are only actually partly formed, with the molecule being the transition state. To be able to compare bonds, I'm using experimental values for the mean C-C and C=C bond lengths[2] which are 1.43Å for carbon carbon single bonds, and 1.54Å for carbon-carbon double bonds. The C-C bond from the ethylene is now at 1.383Å, which is longer than a normal C=C bond, because the bond is changing from double to single in this transition state. The terminal double bonds on the cis-butadiene are now longer, again due to the change from being short double bonds to longer single bonds. However, the single bond that used to exist in the centre of cis-butadiene is now shorter in this transition state (1.398Å), as it also changing bonding type - but from a long single bond to a shorter double bond. In the transition state, bonds are in the process of being broken, and other bonds are in the process of being formed, so all the bonds which are getting longer, are likely to be losing sp2 character and gaining sp3 character, and the bonds decreasing in length are most likely to be losing their sp3 character, whilst gaining sp2 character.
If we look at the molecular orbitals of this transition state, we can see the LUMO of the molecule is symmetric, and the HOMO is antisymmetric. Being the transition state, the molecular orbitals are made by the interactions of the reactants, and so we can compare the molecular orbitals found earlier, to the molecular orbitals here. The asymmetric HOMO of the transition state has been generated by the asymmetric HOMO of the cis-butadiene and LUMO of the ethylene. The symmetric LUMO of the transition state must also have been made from the symmetric LUMO of the cis-butadiene and the HOMO of the ethylene.
 |
 |
 |
 |
The vibrational analysis of this transition state does show an imaginary vibration at -956cm-1, so the transition state has been found. As with all of the previous transition sates, this imaginary vibration corresponds to the reaction pathway. We can also see from the vibration that both sigma bonds are created in a concerted fashion.
The final stage of this Diels-Alder study is to look at a more complicated Diels-Alder reaction - one which can produce more that one product. The Diels-Alder reaction between maleic anhydride and cyclohexa-1,3-diene gives two products - an endo and an exo. A feature of Diels-Alder reactions is that the major product is the one with the lowest activation energy i.e. the route with the most stable transition state, in other words, the reaction undergoes kinetic control.

As we've been told that the endo product is the major product, we know that the endo transition state must be the most stable of the possible transition states.
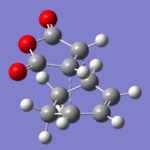
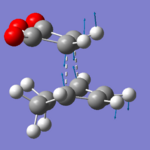
The two product molecules were created in Gaussview, and then optimized with AM1/3-21G to a minimum. The bonds that are created during the transition state were then removed, and replaced with a dashed bond. The two molecules were then put through a freq+opt job in Gaussian, using AM1/3-21G and TS(Berny). Due to the size of the molecules, I decided to run the jobs with calculation of the force constants at every point.
Two transition state molecules were produced, as confirmed by their imaginary vibrations. The total energy for the endo transition state structure was calculated to be -0.0515 Hartrees, and the total energy for the exo transition state structure was -0.0504 Hartrees. This coincides with the theory that the endo transition state was the most stable, as it was the major product. The reason that the endo transition state structure is more stable, is that the exo structure has greater steric interactions, between the oxygen atoms and the non-planar hydrogens on the bridge. The endo structure has the oxygen atoms over a planar area, and so the interactions are lower. Plus, by looking at the through space distance between the maleic anhydride oxygen atoms, and the other substituents in the molecule, we can see that the oxygen atoms in the exo isomer are closer to the groups, increasing sterics, and therefore destabilising the molecule.
 |
 |
 |
 |
 |
 |
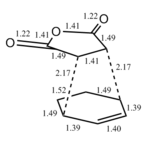
The two sigma bonds formed in the transition state, are shorter in the endo transition state (2.16Å vs 2.17Å). This is a small difference, which must be down to the steric interactions between the bridge and the maleic anhydride part of the molecule - the atoms simply can't get close enough. For both of the transition states, we can see that the C-C carbon bonds within the cyclohexa-1,3-diene ring that are actually involved in the reaction, are all around 1.39Å. For the bond in the maleic anhydride that was previously a double bond, the bond length from both transition state structures, was close to 1.41Å. This length is greater than that of a normal double bond - so we can tell that in both of the transition states, this bond is being converted into a single bond, and is losing its double bond character. The data for both transition states seem show that all bonds that were double within the reactants have been lengthened in the transition states, indicating that they're losing their double-bond characteristics, and becoming single bonds. As before, there is also one bond in the transition state that is shorter than you would expect, and this is because it is now gaining double-bond character.
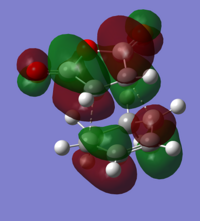
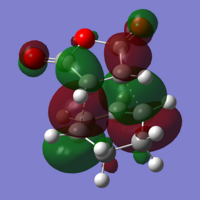
As mentioned above, the frequency analysis of both isomers gives a negative frequency of vibration for each molecule, so both of them are transition states. The imaginary frequency for the exo transition state was -812cm-1, and the endo transition state was -807cm-1.
 |
 |
 |
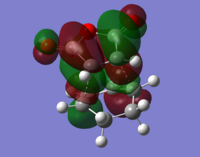 |
As with the previous, more simple Diels-Alder, the HOMO of the diene interacts with the LUMO of the dienophile, to create the observed HOMOs and LUMOs for the two transition states. All of the transition state orbitals were antisymmetric, again reinforcing that the antisymmetric orbitals of the reactants create the antisymmetric orbitals of the transition state. As was mentioned at the beginning, we can't just assume that there is a difference in energies, just because of sterics. A possible stabilising interaction can arise from the 'secondary orbital overlap' of the π orbitals of the -CH=CH-, and the -(C=O)-O-(C=O)- fragment.
However, by examination of the molecular orbitals, it becomes apparent that there are no visible favourable interactions between the orbitals in the endo transition state. This can be for multiple reasons. The most obvious one is that we can't see the orbital overlap, simply because it doesn't exist for this molecule. In this case, the difference in energy between transition states will be solely dependent on sterics. The other option is that the interactions do exist, but the model used in the calculations is unable to take this into account, and so cannot display any of the secondary orbital overlap. As such, a larger basis set might be of more use here.
References and Key Data
- ↑ G. Schultz, I. Hargitta, J. Mol. Struc., 1995, 346, 63-69 DOI:10.1016/0022-2860(94)09007-C
- ↑ L.Bartell, J. Am. Chem. Soc., '1959', 81 (14), 3497-3498. DOI:10.1021/ja01523a002
Log files for "Anti 1", "Anti 2", "Anti 2 (DFT)", "Gauche 1", "Gauche 3".
Log files for "Chair Conformation via Redundant Coordinate Method",
"Chair Conformation via Force Constant Method"
Chk file for "Boat Conformation via QST2"
Log files for "Cis-Butadiene", "Ethylene"
Log file for "100 step IRC of ethene & cyclohexa-1,3-diene"
Log files for "Exo Transition State",
"Endo Transition State"