Rep:Mod3:MJW11

Mike's computational chemistry wiki - MJW11

Module 3

The Cope rearrangement tutorial

The aim of this investigation was to analyse the Cope rearrangment of 1,5-hexadiene using various computational chemistry techniques with the Gaussian software. The Cope rearrangment of 1,5-hexadiene is a classic example of a [3,3]-sigmatropic shift reaction, one class of pericyclic reactions: cheletropic reactions, cycloadditions, electrocyclic reactions and sigmatropic reactions. A pericyclic reaction is ' a type of concerted chemical reaction that proceeds through a cyclic conjugated transition state'.^[1] The concerted formation and breaking of sigma and pi bonds in the sigmatropic reaction is a key feature of its definition. By studying the the reaction pathway for the Cope rearrangment of 1,5-hexadiene, the concerted nature of the reaction can be verified.

Diagram 1 - The cope Rearrangement of 1,5-hexadiene

The investigation was split into two parts: analysis of the reactants and products ( which are indistinguishable in this reaction) and analysis of the transition states. 1,5-hexadiene has many possible conformations available to it, the different conformations of 1,5-hexadiene were analysed in the first part of this investigation. Two possible transition states are thought to be available for the Cope rearrangement of 1,5-hexadiene, a chair and a boat, both of which were analysed in the second part of this investigation. These two analyses were then brought together to gain an understanding of the whole reaction from reactants to transition state to products.

Part 1 - Optimising the reactants and products

The 1,5-hexadiene molecule was modelled in Gausview 5.0 and manipulated such that the central four carbon atoms had an antiperiplanar relationship (dihedral angle of 0^o). This model was then optimised using the Hartree-Fock method with the 3-21G basis set. This procedure was then repeated having manipulated the model such that the central four carbon atoms had a gauche relationship (30^o<Dihedral angle<90^o) Two minimised conformations for 1,5-hexadiene were found using this procedure. Some thought was then put into which possible conformation of 1,5-hexadiene should have the lowest energy. Two factors were deemed important: an anti relationship between the central four carbon atoms and an anti relationship between the terminal carbon atoms to reduce steric clashing between the carbon termini as much as possible. This conformation of 1,5-hexadiene was modelled and optimised. The results of these calculations follow.

Conformer	Energy / Hartree	Relative energy / Hartree	Point group
Anti 3	-231.68907	0.00359	C_2h
Gauche 3	-231.69266	0.00000	C₁
Anti 2	-231.69253	0.00013	C_i

Interestingly, the 'gauche 3' conformation was found to have a lower energy than the 'anti 2' conformation. The 'anti 2 conformation was reoptimised at a higher level of theory, B3LYP/6-31G* to see what effect, if any, this had on the geometry of the conformation. The results follow.

Conformer	Energy / Hartree	Point group
Anti 2	-234.61170	C_i

The total energy of the 'anti 2' conformer was found to be substantially lower (~3 Hartree) at the higher level of theory. The geometry of the conformer, however, did not change substantially. A frequency calculation was run for the 'anti 2' conformer at the B3LYP/6-31G* level of theory to check that the conformer was in fact an energy minimum (negative frequencies suggest insufficient optimisation). 42 molecular vibrations were calculated for the 'anti 2' conformer, all of which were positive. This suggests that 'anti 2' was sufficiently optimised. The results from the frequency calculation follow.

Figure 1 - Calculated infrared spectrum for the Anti 2 conformer of 1,5-hexadiene

The log file from the DFT/B3LYP optimisation of 1,5-hexadiene was inspected to find the energy data for the 'anti 2' conformer. This data was then to be used later when analysing activation energies. These results are presented below.

Thermochemistry results

298.15K

 Zero-point correction=                           0.142491 (Hartree/Particle)
 Thermal correction to Energy=                    0.149847
 Thermal correction to Enthalpy=                  0.150791
 Thermal correction to Gibbs Free Energy=         0.110882
 Sum of electronic and zero-point Energies=           -234.469212
 Sum of electronic and thermal Energies=              -234.461856
 Sum of electronic and thermal Enthalpies=            -234.460912
 Sum of electronic and thermal Free Energies=         -234.500821

0.00K

 Zero-point correction=                           0.142928 (Hartree/Particle)
 Thermal correction to Energy=                    0.142928
 Thermal correction to Enthalpy=                  0.142928
 Thermal correction to Gibbs Free Energy=         0.142928
 Sum of electronic and zero-point Energies=           -234.468775
 Sum of electronic and thermal Energies=              -234.468775
 Sum of electronic and thermal Enthalpies=            -234.468775
 Sum of electronic and thermal Free Energies=         -234.468775

Part 2 - Optimising the chair and boat transition structures


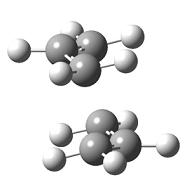
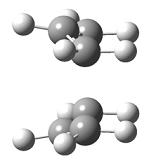
Diagram 2 - Chair transition state for the Cope rearrangement	Diagram 3 - Boat transition state for the Cope rearrangement

Diagrams 2 and 3 show the chair and boat transition states for the cope rearrangement of 1,5-hexadiene. Both transition states show the interaction between two allyl fragments, the only difference between the two transition states is the orientation of each fragment with respect to the other. The chair transition state was analysed first.

Chair conformation

The allyl fragment was modelled using Gaussview 5.0 and optimised at the HF/3-21G level of theory. Two optimised allyl fragments were then orientated with respect to each other such that they resembled the chair transition state in Diagram 2. Two methods were used to analyse the chair transition state: a TS(berny) optimisation and the frozen coordinate method.

Method 1 - TS(berny)

One negative vibrational frequency was found at -817.94 cm^-1. This vibration was identified as being the Cope rearrangement vibration for the chair transition state (Cope rearrangement vibration animation) and clearly shows that the structure analysed here is a transition state in the Cope rearrangement. The distances between the non bonded carbons were found to be 2.02044 Å and 2.02037 Å. The difference between these distances is within Gaussian error limits, the distances between the non bonded carbon atoms are therefore both 2.02 Å.

Method 2 - Frozen coordinate method

The terminal carbons on each allyl fragment were fixed a set distance away from each other (2.20 Å) and the chair conformation transition structure was then optimised to a mimimum. This minimum conformation was then reoptimised along the previously frozen lines between the allyl termini. Using this method, the distances between the non bonded carbon atoms were found to be 2.02066 Å and 2.02060 Å, the difference again within Gaussian error limits.

Both methods therefore produced the same geometry for the chair transition state conformation.

Boat conformation

The boat transition structure was not started from in this calculation but was reached from the reactant using the QST2 method. The QST2 method interpolates between the reactant and product of a reaction to find the transition state. The DFT/B3LYP optimised 'anti 2' model was used as both the reactant and the product in this part of the investigation, having made sure to differentiate between the two by changing the labelling of each atom so as to relate to the sigmatropic reaction here described. The HF/3-21G method was used for the QST2 transition state optimisation.The first computation failed (Failed optimisation) because the reactant and product had not been sufficiently manipulated for the QST2 method to find the boat transition state.

Diagram 4 - Labelling and conformations of the reactant (left) and product (right) for the Cope rearrangement

The dihedral angles between the central four carbon atoms were changed to 0^o and the two 'inside' carbon to carbon to carbon bond angles were changed to 100^o for both the reactant and the product models. The resulting reactant and product models looked as in Diagram 4. The boat transition state was successfully found this time (Successful optimisation).

One negative vibrational frequency of -839.91 cm^-1 was found in the infrared analysis of the boat transition state. This vibration was identified as being the Cope rearrangement vibration for the boat transition state (Cope rearrangement vibration animation) which clearly shows the concerted breaking and formation of sigma bonds between the allyl fragment termini.

IRC Analysis

In order to bridge the gaps between the reactant (in all of its possible conformations), the transition states and the product (in all of its possible confirmations), the Intrinsic Reaction Coordinate (IRC) method was used. The IRC method follows the minimum energy path from a transition structure to a local minimum (reactant or product). Using this method allows one to work out which conformation the reactant must be in to pass via the chair or boat transition state. The IRC method was therefore used for both the chair and boat transition state. The chair which was used in this part of the investigation was that optimised earlier using the frozen coordinates method. The results follow

Chair conformation


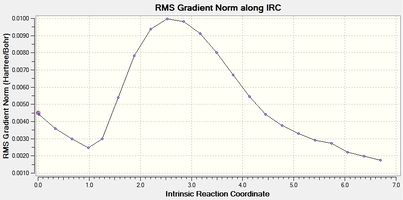
Figure 2 - Graph showing the total energy of the chair conformation (IRC)	Figure 3 - Graph showing the RMS gradient for the chair conformation (IRC)

Figure 3 shows that the IRC method did not reach a minimum energy conformation of the reactant (or product) for the cope rearrangement of 1,5-butadiene from the chair transition state (RMS gradient > 0.001). The IRC calculation was therefore repeated using 50 calculation points and force constants calculated at every point instead of only once.


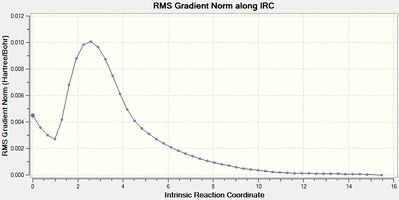
Figure 4 - Graph showing the total energy of the chair conformation (IRC)	Figure 5 - Graph showing the RMS gradient for the chair conformation (IRC)

Figure 5 shows that the IRC method reached a minimum using the greater number of points and force constants calculated at every point of the calculation (RMS gradient < 0.001). The final structure from the IRC method for the chair conformation was minimised using the HF/3-21G level of theory to make sure the structure was a minimum. The product from the IRC calculation for the chair transition state was identified as being the gauche 2 conformer (Energy -231.69167 Hartree, IRC product (chair))

Boat conformation

For the boat conformation, the IRC method was performed using 50 calculation points with force constants calculated at every point of the calculation, as for the chair conformation.


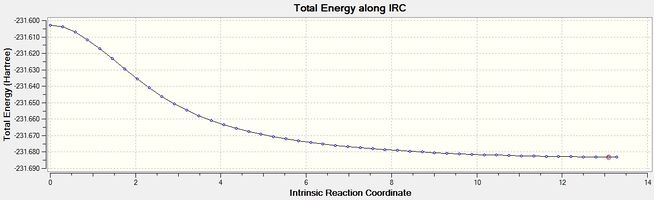
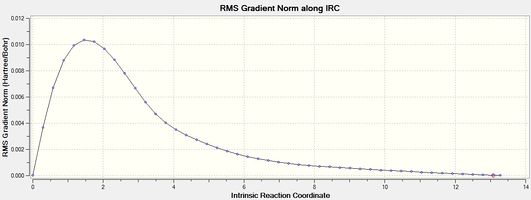
Figure 6 - Graph showing the total energy of the boat conformation (IRC)	Figure 7 - Graph showing the RMS gradient for the boat conformation (IRC)

Figure 7 shows that the IRC method reached an energy minimum (RMS gradient < 0.001). The final structure from the IRC method for the boat conformation was minimised using the HF/3-21G level of theory to make sure the structure was a minimum. The product from the IRC calculation for the boat transition state was identified as being the gauche 3 conformer (Energy -231.69266 Hartree, IRC product (boat))

The HF/3-21G products from the IRC method calculations were then further optimised using the DFT/B3LYP level of theory.

Chair TS HL optimised - -234.55448 Hartree

Boat TS HL optimised - -234.54047 Hartree

Activation energy calculations

Chair TS - 298.15K

 Zero-point correction=                           0.142837 (Hartree/Particle)
 Thermal correction to Energy=                    0.149298
 Thermal correction to Enthalpy=                  0.150242
 Thermal correction to Gibbs Free Energy=         0.113203
 Sum of electronic and zero-point Energies=           -234.411639
 Sum of electronic and thermal Energies=              -234.405178
 Sum of electronic and thermal Enthalpies=            -234.404234
 Sum of electronic and thermal Free Energies=         -234.441273

Chair TS - 0.00K

 Zero-point correction=                           0.143281 (Hartree/Particle)
 Thermal correction to Energy=                    0.143281
 Thermal correction to Enthalpy=                  0.143281
 Thermal correction to Gibbs Free Energy=         0.143281
 Sum of electronic and zero-point Energies=           -234.411195
 Sum of electronic and thermal Energies=              -234.411195
 Sum of electronic and thermal Enthalpies=            -234.411195
 Sum of electronic and thermal Free Energies=         -234.411195

Boat TS - 298.15K

 Zero-point correction=                           0.141958 (Hartree/Particle)
 Thermal correction to Energy=                    0.147884
 Thermal correction to Enthalpy=                  0.148828
 Thermal correction to Gibbs Free Energy=         0.113786
 Sum of electronic and zero-point Energies=           -234.398515
 Sum of electronic and thermal Energies=              -234.392588
 Sum of electronic and thermal Enthalpies=            -234.391644
 Sum of electronic and thermal Free Energies=         -234.426687

Boat TS - 0.00K

 Zero-point correction=                           0.142399 (Hartree/Particle)
 Thermal correction to Energy=                    0.142399
 Thermal correction to Enthalpy=                  0.142399
 Thermal correction to Gibbs Free Energy=         0.142399
 Sum of electronic and zero-point Energies=           -234.398073
 Sum of electronic and thermal Energies=              -234.398073
 Sum of electronic and thermal Enthalpies=            -234.398073
 Sum of electronic and thermal Free Energies=         -234.398073

	Sum of electronic and thermal energies DFT (B3LYP) 0.00K / Hartree	Sum of electronic and thermal energies DFT (B3LYP) 298.15K / Hartree
Anti 2 conformer	-234.461856	-234.468775
Chair transition state	-234.411195	-234.405178
Boat transition state	-234.398073	-234.392588

	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K
ΔE (Chair) kCal/mol	31.79	39.91	33.5 ± 0.5
ΔE (Boat) kCal/mol	40.02	47.80	44.7 ± 2.0

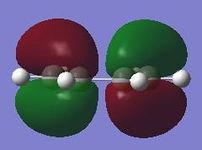
The calculated activation energies at 0.00K and 298.15K show the same trend (activation energy for the chair transition state lower than for the boat transition state) as the experimental values but the 0.00K values are slightly lower than the experimental values. The activation energy for the chair transition state is lower because there is less steric clashing between hydrogen atoms than in the boat transition state. The spatial arrangement of the chair transition state is also more favourable for secondary orbital overlap interactions which are destabilising in this instance. The relevant orbitals have a greater degree of (destabilising) overlap in the boat transition state than in the chair transition state due to the terminal carbon atoms being further apart in the chair transition state than in the boat transition state. This effect is illustrated below in Diagram 5.

Diagram 5 - Frontier orbitals and secondary interactions in the Cope rearrangement ^[2]

The Diels-Alder cycloaddition

The aim of this investigation was to study the Diels-Alder cycloaddition. The Diels-Alder cycloaddition, like the Cope rearrangement of 1,5-butadiene is another example of a pericyclic reaction. The Diels-Alder reaction takes place between a dienophile and a conjugated diene. This investigation was split into two parts: the analysis of the Diels-Alder reaction between butadiene and ethene (the prototypical Diels-Alder reaction) and the analysis of the reaction between cyclohexadiene and maleic anhydride, an interesting example of a Diels-Alder reaction which illustrates regioselectivity.

Part 1 - Reaction between butadiene and ethene

Butadiene

A s-cis butadiene model was optimised using the semi-empirical method at the AM1 level of theory. Contour plots of the molecular orbitals of butadiene were generated and are presented below.

HOMO
LUMO

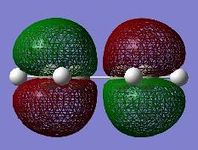
The molecular orbital contour plots for butadiene show that the HOMO is antisymmetric with respect to a plane bisecting the central four carbon atoms, perpendicular to the plane of the molecule. The plots also show that the LUMO is symmetric with respect to the same plane.

Ethene

An ethene model was optimised using the semi-empirical method at the AM1 level of theory. Contour plots of the molecular orbitals of ethene were generated and are presented below.

HOMO	LUMO

The molecular orbital contour plots for ethene show that the HOMO is symmetric with respect to a plane bisecting the carbon to carbon bond, perpendicular to the plane of the molecule. The plots also show that the LUMO is antisymmetric with respect to the same plane.

Transition state

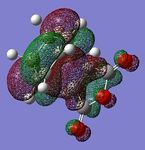
The transition state for this reaction was found by optimising to a TS(berny) at the semi-empirical AM1 level of theory, having preconfigured the system into a sensible arrangement first. Contour plots of the generated molecular orbitals were generated and are presented below.

HOMO (antisymmetric)
LUMO (symmetric)

Frequency calculations were performed on the transition state at various levels of theory. One negative vibration frequency was found using each of the methods, corresponding to the Diels-Alder reaction vibration, animations of this vibration are presented below. An animation of the lowest positive frequency molecular vibration is also animated below.

https://wiki.ch.ic.ac.uk/wiki/images/f/ff/Diels_Alder_Vibration.gif - Negative frequency vibration - AM1

https://wiki.ch.ic.ac.uk/wiki/images/1/17/Diels_Alder_Vibration_DFT.gif - Negative frequency vibration- DFT vibration

https://wiki.ch.ic.ac.uk/wiki/images/2/2a/Diels_Alder_Vibration_AM1.gif - Negative frequency vibration - AM1 vibration

https://wiki.ch.ic.ac.uk/wiki/images/d/d4/Diels_Alder_Vibration_AM1_lowestpos.gif - Lowest positive frequency vibration - AM1

The negative molecular vibrations corresponding to the Diels-Alder reaction clearly show synchronous bond formation, as would be expected for this pericyclic reaction (concerted bond formation and beraking). The lowest positive frequency molecular vibration shows asynchronous bond formation and therefore corresponds to a cyclisation reaction as opposed to a cycloaddition. This asynchronous b ond formation has a higher vibrational frequency and is therefore higher in energy, suggesting that this method of bond formation is less energetically favourable than the synchronous bond formation of the Diels-Alder reaction.

The distance between the carbon atoms which form single bonds along the reaction coordinate was found to be 2.12 Å. The distance between the carbon atoms which have their double bonds broken along the reaction coordinate was found to be 1.36 Å. Typical sp³ carbon to carbon bond lengths are 1.54 Å and typical sp² bond lengths are 1.33 Å.^[3] The bond distance found for the forming carbon carbon single bonds between the ethene fragment and the butadiene fragment are larger than typical sp³ bond lengths, as would be expected for a transition state where the bonds are not completely formed. Likewise, the carbon carbon double bond distances for the ethene fragment and for the terminal carbon carbon double bonds in butadiene are larger than would be expected for sp² carbon carbon double bonds but are less than would be expected for sp³ hybridised carbon atoms. This is again in line with what would be expected for the transition state, where the double bonds are breaking, the relevant carbon atoms are changing from sp² to sp³ hybridisation and thus the bond lengths are larger than in the reactant.

The molecular orbitals for the transition state show that it is the ethene LUMO and the butadiene HOMO which form the HOMO of the transition state. Likewise, the molecular orbitals show that it is the ethene HOMO and the butadiene LUMO which form the LUMO of the transition state. This reaction is allowed because orbitals of the same symmetry combine to form the HOMO and LUMO and have significant (stabilising) overlap.

Part 2 - Regioselectivity

Models of cyclohexadiene and maleic anhydride were optimised at the semi-empirical AM1 level of theory. These optimised models were then manipulated into two 'guess' arrangements, one for the endo transition state and the other for the exo transition state. These were then optimised to transition states using the frozen coordinate method. Models of the endo and exo products of the Diels-Alder reaction are presented below.

Endo transition state

Exo transition state

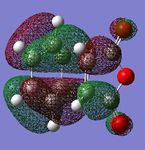
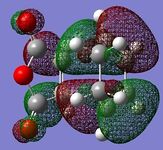
Contour plots of the molecular orbitals of the endo and exo transition states were generated and are presented below.

Endo

Exo

HOMO
LUMO
LUMO+1

The HOMOs and the LUMOs of both the endo and exo transition states for the Diels-Alder reaction presented here are anti-symmetric. The LUMO+1s of the endo and exo transition states are symmetric w.r.t the plane bisecting the maleic anhydride through the central oxygen atom.

The exo transition state was found to have an energy of -0.05042 Hartree and the endo transition state was found to have an energy of -0.05150 Hartree at the semi-empirical AM1 level of theory. The endo transition state therefore has a lower energy than the exo transition state, the endo product is therefore the kinetic product. This result seems counter-intuitive without taking orbital considerations into account as there is more steric clashing in the endo product than the exo product which is reflected in the greater energy of the endo product over the exo product. Secondary orbital effects are needed to explain the greater stability of the endo transition state.

IRC calculation


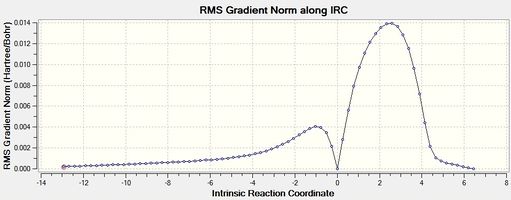
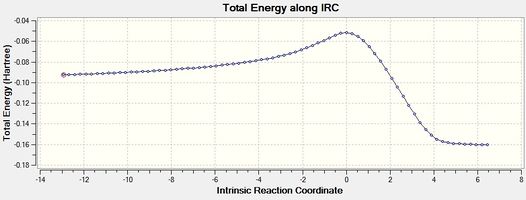
Figure 8 - Graph showing the total energy of the Diels-Alder reaction for the endo product (IRC)	Figure 9 - Graph showing the RMS Gradient of the Diels-Alder reaction for the endo product (IRC)


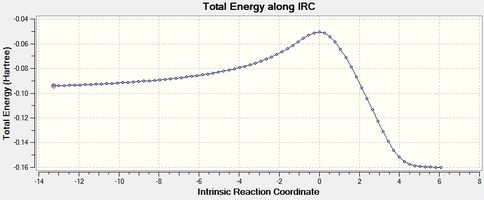
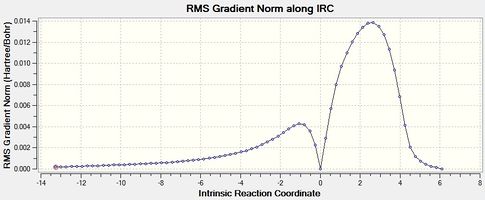
Figure 10 - Graph showing the total energy of the Diels-Alder reaction for the exo product (IRC)	Figure 11 - Graph showing the RMS Gradient of the Diels-Alder reaction for the exo product (IRC)

Figures 8, 9, 10 and 11 show that the Diels-Alder reactions are exothermic as the product energies are visibly lower than the reactant energies. The figures show that the RMS gradients were calculated to be ~ 0 for the reactants, transition states and products as these are stationary states and therefore have a gradient of 0 (no forces acting on the molecule). The RMS gradients a small distance away from the reactants and products via the reaction coordinates stay approximately the same as these represent energy minima. The RMS gradients increase very sharply away from the endo and exo transition states, however, as these represent energy maxima: the transition states are unstable.

The endo product was found to have a total energy of -0.16017 Hartree and the exo product was found to have a total energy of -0.15991 Hartree. This suggests that the endo and exo products have very similar energies and that the endo product is the thermodynamic product of the reaction. The exo product is known to be the thermodynamic product of this reaction however.^[4] The fact that the energies are very close together suggests that the AM1 level of theory is perhaps not sufficient to identify the exo product as the more thermodynamically stable. The AM1 method may not put enough weight on the greater degree of steric clashing in the endo product than the exo product.

Diagram 6 - Secondary overlap of the frontier orbitals of Diels-Alder reactions. The dotted lines show the bonding overlap which stabilizes the endo transition state.

Secondary orbital effects are required to explain the greater stability of the endo transition state over the exo transition state.^[2] Diagram 6 shows the stabilising secondary frontier orbital overlap which exists in the endo transition state but not in the exo transition state, explaining the lower energy of the endo transition state in the reaction presented here.

Conclusion

Many computational chemistry techniques were used in this investigation to help rationalise the Cope rearrangement and the Diels-Alder reaction, both examples of pericyclic reactions. The concerted nature of pericyclic reactions means that computational chemistry techniques are required for complete analysis of the reactions as there are no intermediates, only transition states which are not isolatable in the lab.

The two possible transition states in the Cope rearrangement were found using various methods (QST2, frozen coordinates, TS(berny)) and the greater stability of the chair transition state was found and rationalised. The energetic ordering of the reactant conformers was found and rationalised too. The intrinsic reaction coordinate was used to work out which conformers can access which transition state along the reaction coordinate. The activation energies were then calculated and found to be in agreement with experiment. A higher level method of theory could be used in a future experiment to try and improve the match between the experimental and computed results.

The same techniques were then used to rationalise two Diels-Alder reactions. The computations correctly identified the endo transition state as being more stable than the exo transition state but the endo product was incorrectly identified as more stable than the exo product. Again, a higher level method of theory could be used in a future experiment to try and rectify this. Molecular orbital contour plots were used to rationalise the greater stability of the endo transition state over the exo transition state, making use of secondary orbital effects.

An interesting further experiment would be to analyse a similar Diels-Alder reaction with an unsymmetrical diene or dienophile to further explore the regioselectivity of the Diels-Alder reaction.

References

↑ John Daintith, Oxford dictionary of chemistry, 2008, 403
↑ ^2.0 ^2.1 Ian Fleming, Frontier orbitals and organic chemical reactions, John Wiley & Sons, 2006, 106-107
↑ R. Dias, Organic Chemistry, http://www.odu.edu/~rfdias/chem311/02BONDING.pdf
↑ J. Org. Chem., 2003, 68 (19), 7158–7166