Rep:Mod3:Jazz0611
Zain Khawaja Module 3: Physical Computational Report
Introduction
Computational methods in modern day chemistry have become very useful for studying chemical reactions that may otherwise be difficult to study experimentally. In particular, we can study transition state structures and deduce their energetic position - this is something which tends to be analysed on qualitatively in the laboratory, however calculations via computational means allows us to evaluate the quantitative evidence provided.
In this report, the Cope rearrangement and Diels Alder cycloaddition reactions will be analysed by studying the transition state structures. The use of molecular orbital-based methods will aid in solving the Schrödinger equation and locating and calculating the energy of the transition state on the potential energy surface.
The Cope Rearrangement
Abstract
We can identify the Cope rearrangement as a [3,3]-sigmatropic shift (Figure 1). In this exercise we will be investigating the Cope rearrangement of 1,5-hexadiene. The reaction proceeds in a concerted manner via a cyclic transition state that can adopt two different conformations - chair or boat (Figure 2).
 |
 |
Optimising the Reactants and Products
Since 1,5-hexadiene can exist in various different conformations (different forms of anti and gauche, which we will look at) and each has a slightly different energy to the other, we were able to compare and contrast the structure and energies of the conformations by optimising the geometries to obtain energy values.
1,5-hexadiene was drawn in both the antiperiplanar conformation (where the dihedral angle was 180° between the four central carbons) and gauche conformation (where the dihedral angle was 60° between the four central carbons). Both sets of structures were used as a starting point for the following optimisations. Each structure was optimised using the Hartree Fock method and basis set 3-21G. This gave an optimised geometry for each conformation with an associated energy. Then, we could manually alter the structure (by changing the dihedral angles between the sets of carbon atoms) until we were able to obtain a range of conformations for both the anti and gauche conformations with different energies in order to compare and contrast the most stable of each. Using our supplied literature reference "Appendix 1"[1], we could assign each of our conformers as being identical to those listed in "Appendix 1" by matching our computed energy to that quoted in the literature. The results obtained are shown in the tables below:
| Conformation | Method type | Energy / Hartrees | Point group | Identified conformer from literature[1] | Literature energy[1] |
|---|---|---|---|---|---|
| Conformation | Method type | Energy / Hartrees | Point group | Identified conformer from literature[1] | Literature energy[1] |
|---|---|---|---|---|---|
Prior to the optimisations, we assumed that if we compared the most stable of the two types of conformations (anti and gauche), the gauche conformer would be the less stable due to increased steric repulsion. However the results after optimisation show that if we compare the most stable of the two types of conformation, anti C and gauche A (anti 1 and gauche 3)[1], the gauche conformer is more stable by 0.00005885 Hartrees (0.0369 kcalmol-1). A similar computational study on 1,5-hexadiene was performed by Gung and co-workers, where a similar result was reported. According to their study, this result can be explained by a stabilising attractive interaction between the alkene C=C π-orbital and the vinyl proton C-H σ*-orbital present in the gauche conformer.[2]
The anti E (anti 2) conformer was also optimised using the DFT/B3LYP/6-31G* method and then compared to the optimised structure of the HF/3-21G method. The resulting energies and geometries of the two optimisations are compared in the table below:
| Method type | Energy / Hartrees | Literature energy[1] | Point group | Dihedral angle (C1-C2-C3-C4) / ° | Dihedral angle (C2-C3-C4-C5) / ° | Bond length (C1-C2) / Å | Bond length (C2-3) / Å | Bond length (C3-C4) / Å |
|---|---|---|---|---|---|---|---|---|
We see that the conformer optimised by the DFT/B3LYP/6-31G* method (higher accuracy method) is more stable by 2.92 Hartrees and thus we conclude that the higher accuracy method gives the more stable geometry and is therefore a more accurate method to employ in order to find the energy minimum on the potential energy surface. The DFT method also shows a higher dihedral angle than the HF method. Bond lengths however are seen to be relatively the same at this degree of accuracy (2 dp). At a higher degree of accuracy, we see slight differences.
To confirm this structure as a minimum, a frequency calculation was run. This calculation effectively takes the second derivative of the potential energy surface (curvature). Therefore our output frequencies must result in positive values if we are to assume that we have reached a minimum.
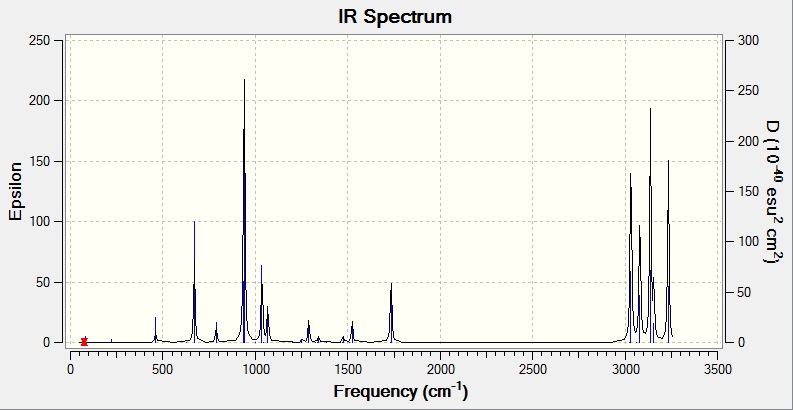
The results showed a minimum obtained since no negative frequencies were found. Moreover, we found proof in the .log file that our calculation had converged successfully. The results from the frequency analysis also give a list of energies which are tabulated in the table below. A computed IR spectrum obtained is also shown.

| Sum of electronic and zero-point energies (Eelec + ZPE) | -234.469198 Hartrees |
| Sum of electronic and thermal energies (E + Evib + Erot + Etrans) | -234.461850 Hartrees |
| Sum of electronic and thermal enthalpies (E + RT) | -234.460906 Hartrees |
| Sum of electronic and thermal free energies (H - TS) | -234.500782 Hartrees |
Optimizing the "Chair" and "Boat" Transition Structures
An attempt will now be made to optimise the transition state structures of the cope rearrangement of 1,5-hexadiene. We can model a guessed transition state initially by optimising an allyl (CH2CHCH2) fragment by the HF/3-21G method and we use this fragment to build up a guessed transition state structure.
We must remember that since we are locating the transition state, we know that we will compute a negative frequency (imaginary) in the frequency analysis. Essentially this is the opposite to a minimisation, in this case we are finding an energy maximum by moving up the potential energy minima (starting from the well and moving upwards).
Chair Transition State
The two optimised allyl fragments were placed next to each other, and the terminal CH2 fragments were distanced 2.20Å apart so that the overall structure was made to look like a chair conformation. An optimisation and frequency analysis was run using the HF/3-21G method on this "guessed" transition state structure.
In order to optimise a transition state, before running the calculation we need to define where the reaction coordinate can be located. Thus this first optimisationg using the "guessed" structure uses the TS Berny method, where we have attempted to optimise a structure which we think is close to resembling the actual transition state structure. Therefore the force constant matrix (Hessian) is easily producable and can proceed throughout the optimisation (which is a step-wise process). The optimised structure geometry can be viewed below.
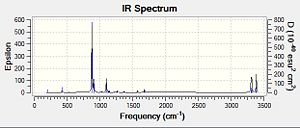
Our calculations computed a final energy of -231.61932239 Hartrees for this transition state. The distance between the terminal ends of the allyl fragments was found to be 2.02Å and the frequency analysis produced an imaginary frequency of 818 cm-1. This vibration and the IR spectrum can be viewed below:
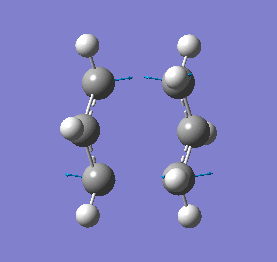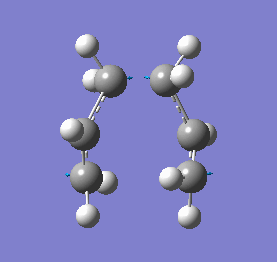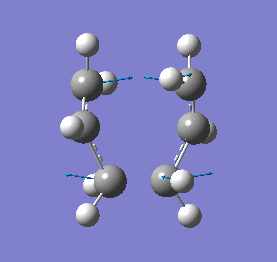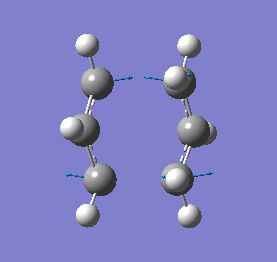 |
 |
By using the frozen coordinate method, a different method to above, we can generate the same transition state structure. By freezing the reaction coordinate and setting the fragments once again 2.20Å apart, with the following results obtained:
Calculations computed an energy of -231.61518495 Hartrees, and a distance of 2.20Å as expected between the terminal carbons of each allyl fragment. This energy is a little higher and tells us we have not quite found the optimised structure. Now we can minimise the rest of the molecule and then optimise again but this time by unfreezing the reaction coordinate. The results are shown below:
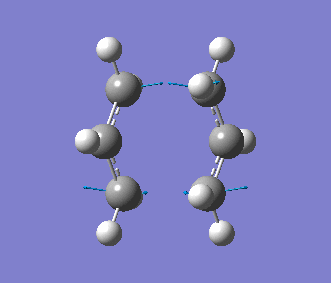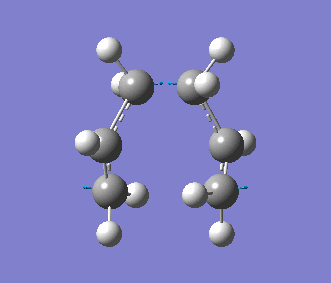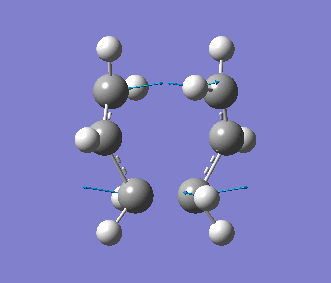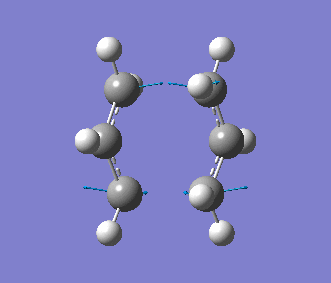
This time, we obtained a final energy of -231.61932247 Hartrees (closer to the energy obtained for the TS Berny Method) and an optimised distance of 2.02Å between the terminal carbons of the allyl fragments. We computed an imaginary frequency of 818 cm-1. Once again, this vibrations and IR spectrum can be seen below:
 |
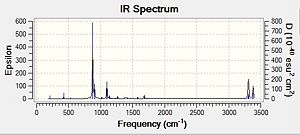 |
The same imaginary frequency and almost the same energy (discrepancies can be attributed to calculation error from Gaussian) were obtained. Therefore we can conclude that both methods obtained the same structure for the chair conformation transition state. Although both methods compute the same final result, we deduced that the frozen coordinate method was more advantageous. The TS Berny method can take longer, especially if we are unable to guess a structure that closely resembles the transition state (or the optimisation would fail). Moreover, the TS Berny method involves computing the entire force constant matrix (Hessian) and essentially finding the derivative along the reaction coordinate. The frozen coordinate saves time if this force constant calculation is likely to take time.
Boat Transition State
To optimise the boat transition state, the QST2 method was used. This time, the method involved defining the reactants and products initially and the optimisation of the transition state geometry was calculated by predicting the structure that lies between the reactants and products. This involved numbering each atom of both structures in a very definitive way as the rearrangement takes place i.e. the carbon set as C1 in the reactants is the terminal carbon in the reactant but in the product, C1 is in fact one of the central carbons (corresponding to the Cope rearrangement mechanism). Thus the structures were numbered to match the mechanism but initial optimisation produced failed results as shown below:
We can see the peculiar geometry obtained by clicking on the button above. This reiterates Gaussian's dependency on the initial "guessed" structure having to be quite similar to the transition state in order for the optimisation to proceed and compute a reasonable structure for the transition state. As a boat transition state was not obtained, the geometry and conformation of the reactant and product structures were altered in order to proceed with an optimisation where the initial "guess" was a better match. Therefore, the central C2-C3-C4-C5 dihedral angle was changed to 0° and the inside C-C-C angles (C2-C3-C4 and C3-C4-C5) were reduced to 100°. This was done for both the reactant and product molecules and the optimisation was attempted again, to yield the following result.
The calculation yielded an energy of -231.60279849 Hartrees and a distance of 2.14Å was found between the terminal carbons of each allyl fragment. This energy is slightly higher than that of the chair structure (chair transition state is more stable by 0.0165239 Hartrees, 43.8 kJ/mol) and this is because the chair is a slightly more stable conformation due to unfavourable interaction between the axial hydrogens present in the boat structure. As a result, the bond distance between the terminal carbons is also a little higher than previously found for the chair structure. An imaginary frequency of 840cm-1 was found. This vibration and the computed IR spectrum can be seen below:
 |
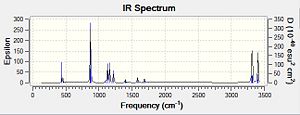 |
Intrinsic Reaction Coordinate (IRC) Analysis
IRC analysis allowed us to find out exactly which conformers the transition state of 1,5-hexadiene leads to. This method involves calculations along the minimum energy path from the transition state down to its minimum on the potential energy surface. It computes a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest. Since the Cope rearragement is reversible and therefore symmetrical, we must define only one direction to run the analysis and naturally pick the forward direction.
Initially we ran IRC analysis for the chair conformation, setting parameters to calculate the force constant at the start and set the number of steps along the IRC to 50 steps. We saw that with these parameters, the minimum energy was not reached, as following the energy pathway, we did not see a convergence to a constant minimum value (the curve did not level off) as shown below by the IRC energy surface below for the chair structure:
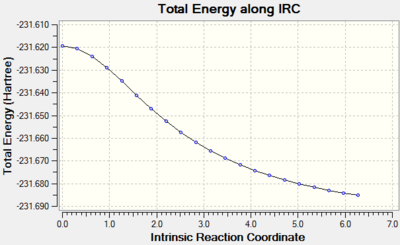
In order to improve the calculation, the IRC was run again but this time the parameters were changed so that the force constant was calculated at each step. This improved the calculation and a minimum was found:
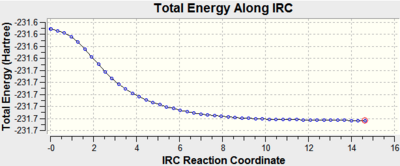
We found that the final energy matched the gauche 2 conformation, as seen in the Appendix[1]
Activation Energies for the Transition state structures
The chair and boat transition state structures were reoptimised by the DFT/B3LYP/6-31Gd method. We can compare these obtained results with those obtained earlier for the optimisations using lower accuracy basis sets:
| HF/3-21G method | DFT/B3LYP/6-31Gd method | |||||
|---|---|---|---|---|---|---|
| Electronic energy / Hartrees | Sum of electronic and zero-point energies / Hartrees | Sum of electronic and thermal energies / Hartrees | Electronic energy / Hartrees | Sum of electronic and zero-point energies / Hartrees | Sum of electronic and thermal energies / Hartrees | |
| at 0 K | at 298 K | at 0 K | at 298 K | |||
| Chair TS | -231.61932247 | -231.466694 | -231.461339 | -234.55698272 | -234.414926 | -234.409007 |
| Boat TS | -231.60279849 | -231.450915 | -231.445282 | -234.54308326 | -234.402349 | -234.396006 |
| Reactant (anti 2) | -231.69253529 | -231.539431 | -231.532566 | -234.61170742 | -234.469198 | -234.461850 |
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.70 | 44.67 | 34.04 | 33.28 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 54.71 | 41.72 | 41.32 | 44.7 ± 2.0 |
We can see that reoptimisation with a higher accuracy basis set results in a lower energy geometry suggesting that it is advantageous to compute the potential energy surface through a low level of theory first, then reoptimise it at a higher level. We could calculate the activation energies above from the thermochemical data and the data shows the chair transition state to be more favourable.
Conclusion
Conclusive evidence from calculations performed above on the reactants, transition states and products allows us to deduce the conformation for each of the given steps of the reaction.
Through the given energy values, geometries and frequency calculations above, we can deduce that in the Cope rearrrangement of 1,5-hexadiene, the reactant adopts the anti 1 or anti C () conformation and the product adopts the gauche 3 or gauche A (). Moreover, the transition state adopts the chair conformation (). [see Wiki Section 2.2 and Section 2.3 for data].
Diels Alder cycloaddition between ethene and cis-butadiene
Introduction
The Diels Alder cycloaddition is an example of a pericyclic reaction. In this reaction, the dienophile and diene π orbitals form new σ bonds with each other. The number of π-electrons involved dictate whether the reaction is possible. If we were to think of it in terms of molecular orbitals, the bond formation involves the HOMO and LUMO of both the dienophile and diene. If the HOMO and LUMO are close in energy to each other and have the same symmetry, this results in favourable overlap and the reaction proceeds favourably.
Molecular orbital analysis of reactants
Both reactant molecules (ethene and cis-butadiene) were optimised using the AM1 semi-empirical molecular orbital method allowing us to visualise the HOMO and LUMO:
| Reactant | HOMO | LUMO |
| cis-Butadiene |  Antisymmetric Energy = -0.342 Hartrees |
 Symmetric Energy = 0.120 Hartrees |
| Ethene |  Symmetric Energy = -0.381 Hartrees |
 Antisymmetric Energy = 0.068 Hartrees |
Viewing the above orbitals, we can see a plane of symmetry perpendicular to the double bonds of both reactants (σv). Since only orbitals of the same symmetry can interact, we can deduce that the reaction proceeds by interaction of the cis-butadiene HOMO and ethene LUMO.
Molecular orbital analysis of transition state
We used the forzen coordinate method to optimise the transition state by the DFT/B3LYP/6-31Gd method. We recalled that the structure of the transition state was an envelope-like structure where overlap between the ethene π orbitals and the π system of butadiene was maximised. We obtained the starting geometry by removing the CH2CH2 fragment after defining the bicyclo system and set the distance between the fragments to 2.2Å. The resulting optimisation is summarised below:
The energy of the transition structure was found to be -231.60320765 Hartrees with one imaginary frequency at 818 cm-1. This vibration corresponds to the simultaneous formation of two C-C bonds at the same time reiterating that the Diels Alder mechanism is concerted.
The MO analysis of the transition state can be seen below:
| MO type | 'Visualisation |
| HOMO | 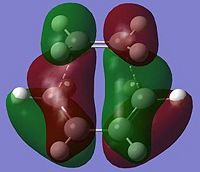 Antisymmetric Energy = -0.323 Hartrees |
| LUMO | 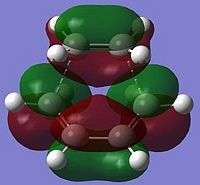 Symmetric Energy = 0.018 Hartrees |
We know in terms of MO rules that two orbitals that interact must be of the same symmetry. By looking at the MOs above, we can see that the HOMO is asymmetric in the transition state, therefore is a linear combination of the ethene LUMO and cis-butadiene HOMO (which are both asymmetric). The LUMO of the transition state is symmetric and thus is a linear combination of the symmetric ethene HOMO and symmetric butadiene LUMO.
Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride
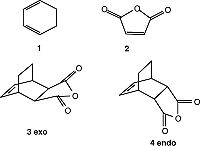
We can study the regioselectivity of the Diels Alder reaction by analysing this reaction. This time we are looking at a Diels Alder reaction where there are substituents located on both the diene and dienophile. The reaction of the two reactants results in the endo product is the the major product via a kinetically controlled pathway with the endo transition state being more stable. As the reaction is in kinetic control anyway, it is expected the exo product would be higher in energy anyway. By using the frozen coordinate method and an AM1 calculation, obtained the following results:
The structure is confirmed as a transition state by the presence of an imaginary (negative) frequency. A negative frequency value, where the frequency is calculated as equivalent to the second derivative confirms the transition state as a maximum (since a negative second derivative signifies a maximum on the potential energy surface). As previously discussed, this vibration describes a synchrous bond formation highlighting the concerted nature of the Diels Alder pericyclic reaction.
In terms of chemical intuition, we expect the exo transition state and therefore product to be more stable due to less steric clash in the structure. We see 1,3-diaxial interactions between the hydrogens in the endo transition state. However the results above show the endo transition state to be more stable. This can be explained by secondary orbital interactions that stabilise the endo transition state, shown in the picture on the right (this secondary orbital interaction is shown for much simpler molecules for clarity):
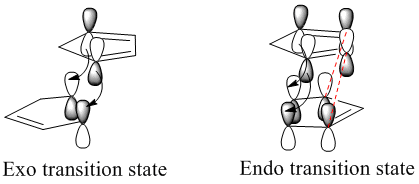
As stated earlier, the reaction proceeds by a Diels Alder style mechanism, so the two different products are brought about by two differing transition state orientations (differing approach of the reacting dienophile to the diene). By observing the secondary orbital interactions in the transition state of the endo product (interactions which are not present in the exo product transition state) we can observe how there is a non-bonding interaction between the antibonding p orbitals of the back of the diene structure with the dienophile, thus the endo transition state is stabilised relative to the exo transition state (endo rule).
Both HOMO and LUMO are asymmetric, thus confirming the rule that only orbitals of same symmetry can interact in bond formation and bond breaking. The Endo MOs are signifantly denser with electron density, suggesting that this secondary orbital overlap is present and viewable, confirming our prediction that the endo transition state is more stable, thus the endo product is the major product.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Appendix_1
- ↑ B.W.Gung, Z.Zhu, R.A.Fouch, J. Am. Chem. Soc., 1995, 117 (6), pp 1783–1788 DOI:10.1021/ja00111a016
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#The_Diels_Alder_Cycloaddition