Rep:Mod3:DL2310
Introduction to Module 3
One of the most often encountered problem in chemistry is to determine the reaction mechanisms. The reactants and products can be thouroughly understood with the experimental techniques available, however it is very hard to determine exactly how the reactants become product. The transition states are by definition high in energy and cannot be isolated, thus we know very little about them from experimental data. Theoretical methods like molecular orbitals analysis can yield good approximations for some systems. Computational chemistry has a good advantage over experimental chemistry to predict energies, molecular orbitals and transition states which can't be observed in the laboratory. [1]. Once the structures of the transition states are known, the chemical pathways are more easily determined. The recent development in technology provides us with a good understanding of mechanisms through Potential Energy Surfaces (PES). A PES is a surface that shows how the energy varies with small variations in the structure of a molecule.
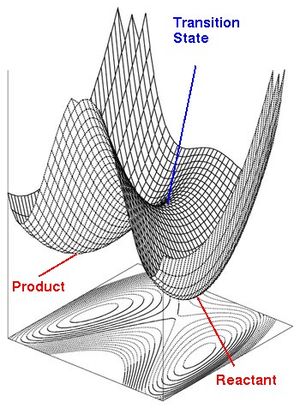
In molecules containing more than three atoms, there are too many degrees of freedom to map out each point discretely. Instead, the Born- Oppenheimer approximation is used and the surface is characterised by its critical points. These are the minima, and saddle points, they determine the molecular structures of the reactants and products (minima) and of the transition states (saddle points). The reaction pathway can be thought of as a series of steepest descent steps linking the critical points together.
The aim of this module is to locate and characterise the transitions states involved in two organic synthesis reactions, the Cope rearrangement and a Diels-Alder Reaction.
The Cope Rearrangement
The Cope rearrangement is a [3,3] sigmatropic rearrangement with only carbons on a ring [3]; for which the reaction mechanism was subject to controversy. In this part of the module, we are going to investigate hexadiene and its rearrangement occurring via a chair or a boat .

Conformational Analysis of 1,5 Hexadiene using the HF/3-21G basis set for optimisation
Hexadiene can adopt several conformations and all are not of the same energy. In this section, several conformations of hexadiene are modelled and optimised to assess their energies. One Particular conformation is further optimised and analysed to understand the reaction pathway of the rearrangement.
An anti linkage and gauche linkage structures were optimised with the same method which enables us to compare their energies. Usually, a gauche conformation would be expected to be higher in energy than an anti conformer due to repulsion of the substituents that are close to each other. However, this is a medium chain length and there can be some positive interactions due to the donation of electron density from the pi orbital of a double bond into an empty sigma star orbital nearby and vice versa in some of the gauche conformations[4]. The lowest energy conformation is predicted to be the "gauche 3" conformation. This was checked against the appendix 1 of the script [5]
| Conformation | Energy (a.u.) | Point group | Structure |
| Anti 1 | -231.69260237 | C2 | 
|
| Gauche 6 | -231.68916020 | C1 | 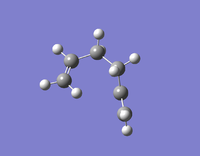
|
| Anti 2 | -231.69253528 | Ci | 
|
| Gauche 5 | -231.68961573 | C1 | 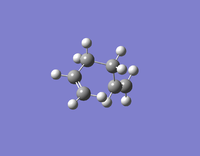
|
| Gauche 3 | -231.69266122 | C1 | 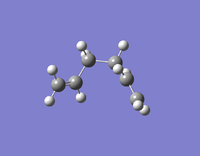
|
Proof of competion of the optimisations
Anti 1
Item Value Threshold Converged?
Maximum Force 0.000033 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000373 0.001800 YES
RMS Displacement 0.000081 0.001200 YES
Predicted change in Energy=-3.986209D-09
Optimization completed.
-- Stationary point found.
Gauche 6
Item Value Threshold Converged?
Maximum Force 0.000019 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000228 0.001800 YES
RMS Displacement 0.000077 0.001200 YES
Predicted change in Energy=-3.556524D-09
Optimization completed.
-- Stationary point found.
Anti 2
Item Value Threshold Converged?
Maximum Force 0.000060 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000565 0.001800 YES
RMS Displacement 0.000171 0.001200 YES
Predicted change in Energy=-2.036691D-08
Optimization completed.
-- Stationary point found.
Gauche 5
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.001173 0.001800 YES
RMS Displacement 0.000335 0.001200 YES
Predicted change in Energy=-3.412032D-08
Optimization completed.
-- Stationary point found.
Gauche 3
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000689 0.001800 YES
RMS Displacement 0.000215 0.001200 YES
Predicted change in Energy=-6.666391D-09
Optimization completed.
-- Stationary point found.
Optimisation of 1,5 Hexadiene anti2 conformation to the DFT/6-31Gd level
The overall structure of the molecule does not change much with the higher basis set optimisation. The energies cannot be compared as the basis set is different, the minimum energy is therefore not calculated the same way and gives rise to large variations.
| Optimisation level | Energy in a.u. | Point Group | Terminal C=C bond length in A | CH-CH2 bond length in A | middle CH2-C2 bond length in A |
| 3-21G | -231.69253528 | Ci | 1.32 | 1.51 | 1.55 |
| 6-31G | -234.61173013 | Ci | 1.33 | 1.50 | 1.55 |
| Literature[6] | N/a | N/a | 1.34 | 1.51 | 1.54 |
Proof of completion
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000227 0.001800 YES
RMS Displacement 0.000083 0.001200 YES
Predicted change in Energy=-1.557146D-08
Optimization completed.
-- Stationary point found.
Frequency Analysis of 1,5 Hexadiene anti2 conformation
The energy information given by the optimisations represents the energy of the molecule on the bare potential energy surface. To be able to compare those energies with experimental values, new terms need to be added to the calculation, this therefore requires a frequency analysis. The frequency analysis can also be used to determine if the molecule is indeed the lower in energy and characterise the critical point. This is done by looking at the frequencies of the vibrations and determining if all are real- ie. positive. The low frequencies should also be small and within the -15 to 15cm-1 range.
The IR Spectrum All the vibrations are positive and therefore real.
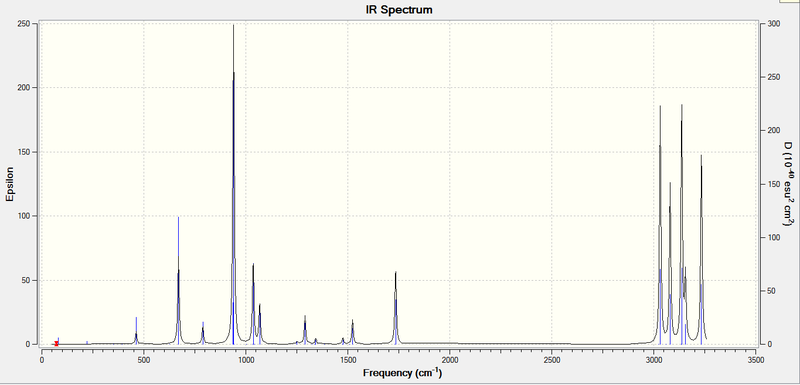
The low frequency data
Low frequencies --- -0.0004 0.0008 0.0011 5.9833 11.2449 26.0149 Low frequencies --- 73.0909 81.6777 120.5770
Proof of completion'
Item Value Threshold Converged?
Maximum Force 0.000035 0.000450 YES
RMS Force 0.000013 0.000300 YES
Maximum Displacement 0.000204 0.001800 YES
RMS Displacement 0.000105 0.001200 YES
Predicted change in Energy=-1.406674D-08
Optimization completed.
-- Stationary point found.
Thermochemistry Data
Thermochemical data about the energies of the Anti 2 confomer.
In order, this data outlines:
(i) the potential energy at 0K taking zero-point vibrational energy into account: E0 = Eelec + ZPE;
(ii) the energy at standard conditions including translational, vibrational and rotational contributions to the total thermal energy: E = E0 + Evib + Erot + Etrans;
(iii) the energy containing a correction term for RT which is particularly significant when looking at dissociation reactions: H = E + RT;
(iv) the energy including entropic contributions: G = H - TS All energies are in a.u.
Sum of electronic and zero-point Energies= -234.469213 Sum of electronic and thermal Energies= -234.461865 Sum of electronic and thermal Enthalpies= -234.460921 Sum of electronic and thermal Free Energies= -234.500796
Optimising the "chair" and "boat" structures
There has been some controversy about the structure of the transition states of the Cope rearrangement, however it is now largely acknoledged that the sigmatropic rearrangement goes through a boat or chair type transition state. In the 1,5 Hexadiene case, the transition state is essentially a pair of CH2CHCH2 allyl fragments one on top of the other. The two fragments can stack in two different ways producing a "boat" (C2v) structure and a "Chair" (C2h) structures.
In this section, an allyl fragment is going to be optimised and from that structure, several methods will be used to optimise the two TS. The optimisation of an existing molecule is fairly straight forward, as the molecule is optimised to a minimum. Things get a bit more complicated when the subject of the calculation is a transition state as the calculation needs to know where the negative direction of curvature (the reaction coordinate) is. A successful optimisation and frequency analysis of a TS shows one negative imaginary frequency.
HF/3-21G optimisation of an Allyl fragment
proof of completion
Item Value Threshold Converged?
Maximum Force 0.000102 0.000450 YES
RMS Force 0.000049 0.000300 YES
Maximum Displacement 0.000794 0.001800 YES
RMS Displacement 0.000306 0.001200 YES
Predicted change in Energy=-1.644637D-07
Optimization completed.
-- Stationary point found.
Optimisation of the Chair Transition State
It is much easier for Gaussian to reach the global maximum energy point when the proposed structure is a close guess.
Method 1 (b)
The first approach towards an optimised chair TS was to use a guess structure. Two of the previously optimised allyl framents were stacked in a chair TS structure with the bond forming/breaking carbons 2.2 Angstrom away from each other to mimic the transition state. An Optimisation+Frequency analysis was then run on the guess structure using the TS Berny job type and with the HF/3-21G method. The additional Opt=NoEigen was used to prevent early termination of the calculation in order to make sure we reach the global saddle point and not just a local one.
The resulting structure shows shorter fragment separation (2.02A) and an imaginary frequency at -818cm-1
Frequencies
Low frequencies --- -817.8840 -4.7960 -2.9436 -0.0005 0.0005 0.0006 Low frequencies --- 4.3245 209.5194 396.0651 ****** 1 imaginary frequencies (negative Signs) ******

proof of completion
Item Value Threshold Converged?
Maximum Force 0.000062 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000499 0.001800 YES
RMS Displacement 0.000088 0.001200 YES
Predicted change in Energy=-5.160156D-08
Optimization completed.
-- Stationary point found.
The .log file can be found here.
Method 2 (c and d)
The second approach towards the Chair TS was a frozen coordinates method. The original guess structure is set to have frozen bond breaking/making distances at 2.2A. This method can easily fail if the frozen distances is too far from the real structure; it is therefore a good method to use when literature values are available. A keyword Opt=ModRedundant is added to the calculation. The job type was still an Opt+Freq with a TS Berny, however, the "bond" input was changed to "derivative" and no force constants were calculated. The structure obtained from the calculation is similar to the one from method 1. There is still the same unique imaginary frequency and similar bond length (2.02A)
Frequency
Low frequencies --- -818.0109 -5.0720 -4.7239 0.0008 0.0009 0.0009 Low frequencies --- 3.6620 209.5010 396.2705 ****** 1 imaginary frequencies (negative Signs) ******
proof of completion part c
Item Value Threshold Converged?
Maximum Force 0.000057 0.000450 YES
RMS Force 0.000015 0.000300 YES
Maximum Displacement 0.001706 0.001800 YES
RMS Displacement 0.000279 0.001200 YES
Predicted change in Energy=-4.504416D-07
Optimization completed.
-- Stationary point found.
proof of completion part d
Item Value Threshold Converged? Maximum Force 0.000028 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.002387 0.001800 YES RMS Displacement 0.000344 0.001200 YES Predicted change in Energy=-5.674752D-07
Comparison of the structures obtained for the Chair TS
| Method | Terminal Bond Length | Energy | Imaginary Frequency |
| Method 1(b) | 2.02Å | -231.6193 | -817.9 |
| Method 2 (c&d) | 2.02Å | -231.6193 | -818.0 |
Both methods yield the same separation distance between the two fragment ends. The value of 2.02Å is smaller than the guess structure value however, the optimisations were successful as convergence points were found as shown previously. This value is also much larger than a normal C-C single bond (1.54Å[7]), suggesting that this is a partially formed bond and supports the hypothesis that this structure is indeed a TS.
Optimisation of the Boat TS
Method 1 (e)
The first approach towards a boat TS was a QST2 method. This method involves the drawing of the reactant and product structures with correct numbering; and allowing Gaussian to interpolate between them and find the TS. The Opt+Freq (QST2) was run at a HF/3-21G level.

The resulting structure was a chair-like structure and not a boat. The reason for the failure of the calculation is that the allyl fragments were not allowed to rotate.
IMAGEAdd IMAGE of the CHAIRBOAT HERE
Now to make the calculation work, the fragments had to be adapted to look more like the Boat. The dihedral angle was manually changed to 0°. The angles of the C-C-C (ie. C2-C3-C4 and C3-C4-C5) were changed to 100°. The same QST2 calculation was run again.
The structures of the adapted fragments and the boat TS are as follows:
 |
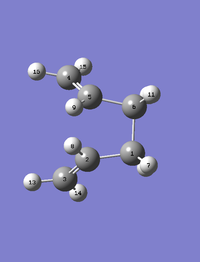 |
 |
Frequency Only one imaginary frequency is observed.

Low frequencies --- -840.2037 -1.5542 -0.0010 -0.0006 0.0019 4.2284 Low frequencies --- 7.6247 155.3739 382.0814 ****** 1 imaginary frequencies (negative Signs) ******
Proof of completion
Item Value Threshold Converged?
Maximum Force 0.000092 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.001121 0.001800 YES
RMS Displacement 0.000371 0.001200 YES
Predicted change in Energy=-2.345278D-07
Optimization completed.
-- Stationary point found.
Intrinsic Reaction Coordinate (f)
After optimising the reactants, products and Transition states that could exist between them, it is still not possible to predict the which initial conformer of 1,5 Hexadiene will generate the transition structure. In order to determine this, the Intrinsic Reaction Coordinate (IRC) job has to be run. This method allows us to follow the reaction path by following the curve of minimum energy from the transition structure to the product.
This did not work for me. The experiment was run several times and the calculation never proceeded.
Nevertheless, the result of this calculation should give a structure that is not a minimum as shown by the lack of convergence. There are then three methods that can be used to reach the minimum structure.
Method 1, the last point on the IRC can be taken (ie. the structure obtained that is not a minimum) and minimised. This is a quick method that can work well as long as the structure to minimise is not too far off or it might go down the wrong pathway.
Method 2, the IRC can be rerun using a larger number of points. This is more reliable than method 1 but if too many points are included, the calculation can also take the wrong pathway and end up with the wrong conformation.
Method 3, the IRC calculation can be rerun but this time computing the force constant at every step. This is the most reliable method but it is expensive and cannot always be applied to larger systems.
For the initial calculation, the reaction coordinate was computed in the forward direction only as our system is symmetrical. The numbers of points along the IRC was set to 50 and the calculation never started as the following error appeared. "Severe Error Message # 2070 The processing of the last link ended abnormally. All processing has been aborted"
Activation Energies (g)
The activation energies for each TS can be calculated from higher level optimisations. The HF/3-21G optimised TS structures were therefore further optimised to the DFT B3YLP 6-31G (d) level and a frequency analysis at that level was run.
The Chair TS
The Optimisation did not work, the same error message was displayed and this part can't be presented.
The Boat TS
The Optimisation did not work, the same error message was displayed and this part can't be presented.
Energy comparison
The Optimisations did not work, and this part can't be presented.
Diels-Alder Reaction
The Diels-Alder reactions are pericyclic reactions and a very powerful tool in the making of new Carbon-Carbon Bonds. To be a pericyclic reaction, the Diels-Alder consists of a concerted reaction of a diene and dienophile with no intermediates and a transition state with aromatic character[8]. This process is made possible by the interaction between the two fragments' HOMO and LUMO. Whether the reaction will happen or not and at which rate largely depend on the interaction between those orbitals between the two fragments. The HOMO of one of the reactants has to be able to interact with the LUMO of the other. And they interact only if there is a significant overlap between them ie. similar size, shape, symmetry and energy.

The aim of this part of the module is to investigate the Diels-Alder reaction with a simple model consisting of ethene and Cis butadiene. However, it is well known that adding substituents on the diene and dienophile affect the HOMO and LUMO's energies which can make the reaction easier and quicker. We will therefore explore the same system with substituents attached.
In this part of the module, all the calculations will be run with semi empirical methods.
Cisbutadiene

| Terminal C=C bond length | Central C-C bond length | C-H bond length | C=C-C Bond angle | Energy |
| 1.34A | 1.45A | 1.10A | 126° | 0.04879719 a.u. |
Proof of completion
Item Value Threshold Converged?
Maximum Force 0.000030 0.000450 YES
RMS Force 0.000011 0.000300 YES
Maximum Displacement 0.000366 0.001800 YES
RMS Displacement 0.000162 0.001200 YES
Predicted change in Energy=-9.691108D-09
Optimization completed.
-- Stationary point found.
The HOMO and LUMO
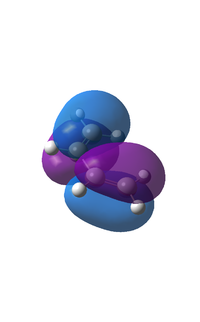 |
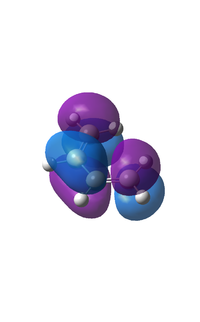 |
The HOMO is anti-symmetric with a node between C2 and C3. The LUMO orbital shows two nodes between C1 and C2 and C3 and C4, it is symmetrical with respect to the plane going through the middle of the central bond of cis-butadiene. It can be noticed that the orbitals calculated correspond closely to the theoretically LCAO derived orbitals shown in the scheme in the introduction.
The transition state of the Diels-Alder reaction between ethene and cis-butadiene
The Guess structure of the Diels-Alder reaction was drawn using the bicylo-octane template, adding the necessary double bond and deleting a -CH2-CH2- fragment. The bond forming distances were then set to 2.2A. A semi-emipirical AM1 job was then run on that structure. The job ran for a long time before displaying the same error message, this part and all the following cannot be presented.
Study of the regioselectivity of the Diels-Alder reaction
The Optimisations did not work, the same error message was displayed and this part can't be presented.
References
- ↑ H. MaskillThe Investigation of Organic Reactions and Their Mechanisms, 2006, Blackwell Publishing Ltd.
- ↑ http://www.chm.bris.ac.uk/pt/harvey/elstruct/hf_2.html
- ↑ Clayden, J.; Greeves, N.; Warren, S.; Wothers, P.; Organic Chemistry, 2011, Oxford University Press.
- ↑ Gung, B. W.; Zhu, Z.; Fouch, R.; J. Am. Chem. Soc., 1995, 117, 1783-1788. DOI:10.1021/ja00111a016
- ↑ M.Bearpark., (2012)., Moecule 3, Physical (Computational Lab)., [Lab Script]., Imperial College London., Autumn 2012.,Lab Script
- ↑ G. Schultz, I. Hrgittai, J. Mol. Struct., 1995, 346,63-69
- ↑ Schultz, G.; Hargittai, I.; J. Mol. Struc., 1994, 346, 63-69. DOI:Error: Bad DOI specified!
- ↑ Da Silva Filho, L. C.; Lacerda, V. Jr; Constantino, M. G.; Da Silva, G. V.; Beil. J. Org. Chem., 14, 2005, 1-5. DOI:10.1186/1860-5397-1-14
