Rep:Mod3:CosGot
3rd Year Computational Chemistry Lab Report - Module 3
Student: Cosma Gottardi (Ceg08)
Part one: the Cope rearrangement
The first part of this report will analyse the mechanism of the Cope Rearrangement, the model example of a concerted [3,3]sigmatriopic reaction. First we will analyse and optimise the structure of the reactant, 1,5-hexadiene, which incidentally here is also the product, before we look more closely at the transition state.
All calculations were carried out using Gaussian 3 via the GaussView 3.09 interface unless otherwise mentioned.
Optimisation of the structure of hexa-1,5-diene
A conformer of hexa-1,5-diene (1) with the 3C-4C bond anti-periplanar (app) was drawn in GaussView and optimised at using the HF/3-21G method (logfile,) - the resulting conformer molecule had an energy of -231.69260 Hartree, which belonged approximately to the C2 point group. Next, a different conformer of 1 was drawn, with a synclinal 3C-4C bond, which after the same type of optimisation (logfile,) had an energy of -231.69167 Hartree, i.e. about 2.4 kJ/mol higher, also having C2 symmetry. Starting with this conformation, the 2C-3C bond was rotated by 120° to give (after optimisation, logfile,) a third conformation, with an energy of -231.69266 Hartree (which is 0.16 kJ/mol lower than the first) with C1 symmetry. This conformation corresponds to the gauche3 conformation in the table in the appendix of the question, and has been found there to be the lowest energy conformation of 1. A fourth conformer, named anti2, that has Ci Symmetry, in which the plane defined by the first three carbon atoms is parallel to that defined by the latter three with an app linkage between the two central carbon atoms, was first optimised using the less sophisticated HF/3-21G method basis set (logfile,) but then refined further using a DFT method, RB3LYP/6-31G(d) (logfile,), which takes into account contributions from more atomic orbitals. It is interesting to compare these two methods in terms of the models they yield, in terms of the geometric parameters we find from the calculations:
| Geometric feature | HF/3-21G | RB3LYP/6-31G(d) |
|---|---|---|
| 1C=2C double bond length | 1.316 Å | 1.333 Å |
| 2C-3C bond length | 1.509 Å | 1.504 Å |
| 3C-4C bond length | 1.553 Å | 1.548 Å |
| distance from 1C to 6C | 5.94 Å | 6.02 Å |
| H-3C-H angle | 107.7° | 106.6° |
| 2C-3C-4C angle | 111.3° | 112.7° |
| torsional angle between two gauche H on the 3C-4C bond | 62.8° | 64.1° |
| torsional angle between the two gauche H on the 2C-3C bond | 55.8° | 60.0° |
The bond lengths are virtually the same in both methods, the double bonds being slightly longer and the single bonds slightly shorter. The conformer having Ci symmetry, it is exactly symmetric across the central C-C bond. The angles are also fairly similar, being not more than 2° apart, however several torsional angles are up to about 5° different, which must be due to the different ways of calculating steric repulsions and the electronic interactions between the two methods. Overall the length of the molecule increases by 0.08 Å, which is very little, being just slightly more than a percent.
To confirm that this structure is in fact an energy minimum, a frequency analysis was carried out using the same method and basis set(logfile). Of the 42 vibrational frequencies found, none were negative (i.e. imaginary), and the following table summarises some thermochemical properties also calculated, which unlike the total energy (-234.6117 Hartree for this conformation) found in the geometry optimisation, can be used for comparison with experimental data.
| Property | Symbols for Energies | Energy / Hartree |
|---|---|---|
| Sum of electronic and zero-point Energies | E(0 K) = Eelec + ZPE | -234.4692 |
| Sum of electronic and thermal Energies | E(298.15 K) = E(0 K) + Evib + Erot + Etrans | -234.4618 |
| Sum of electronic and thermal Enthalpies | H = E (298.15K) + RT | -234.4609 |
| Sum of electronic and thermal Free Energies | G = H - TS | -234.5007 |
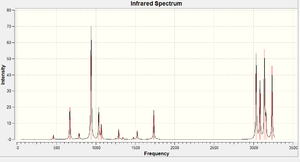
Following the vibrational analysis, the vibrational (IR-)Spectrum of this conformer of 1 could also be predicted. However, one will see that there are not 42 peaks as one would expect when there are 42 different vibrational modes: not because of degeneracy of vibrations, but because of the high symmetry in the conformer; the magnetic dipole moment does not change for half the vibrational modes, and hence these vibrations cannot be excited using (electromagnetic) IR light. Instead one could visualise these frequenciesusing Raman Spectroscopy. In addition to this, there are also some vibrations whose intensities are very low or negligible indeed, for example some bending and twisting modes involve the whole molecule. So on the whole, we can predict to see only see a few peaks.
Transition state modelling
Having modelled several conformations of the reactant and the product of our reaction, we can now turn to analysing the two possible transition states: chair- and boat-like. After finding an acceptable geometry for each of these in different ways using the HF/3-21G method, we re-calculate the energy of these transition states using the more precise RB3LYP/6-31G(d) method to find the respective activation energies for both paths - i.e. the energy difference between the reactant and each transition state respectively.
Modelling the chair transition state by calculating the force constants
An planar allyl fragment was constructed in GaussView and optimised using HF/3-21G. Two of the optimised fragments were inserted into the same GaussView window and arranged so that their planes were approximately parallel with the hydrogen atoms on the central carbon atoms pointing in opposite directions and the distance between two adjacent terminal carbons was set to be exactly 2.2 Å. This approximation to the transition state was optimised, however unlike the previous optimisations, this optimisation aimed not to find a minimum in potential energy, but rather to find a local maximum in one component wile minimising the rest - effectively looking for a saddle point on the potential energy surface: the highest point in one direction (the reaction coordinate) but as low as possible in the other direction(s): a minimum with respect to the other forces acting on the atoms at that geometry. Hence, the TS(Berny) method was used during the optimisation (instead of minimum), and to avoid Gaussian failing the job because of too many imaginary frequencies, Opt=NoEigen was added as a keyword.
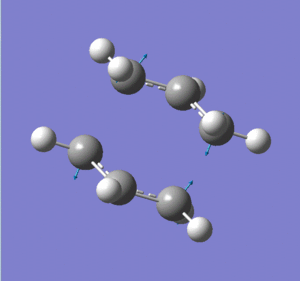
The (chair) transition state thus found (logfile) fortunately only had one negative (imaginary) frequency at -818 cm-1, which can be described as the two fragments rocking towards each other, as if they were reacting backwards and forwards in the Cope rearrangement. For a given geometry, no negative frequencies would mean that we were at a minimum on the potential energy surface, and any negative frequencies mean that we are not at a minimum. However this just one negative frequency tells us that the forces acting on the atoms of our optimised geometry are unstable in just one direction (and stable in all other directions). This confirms that the geometry we have found is indeed a transition state - the one we were looking for.
Modelling the chair transition state using the redundant coordinate editor
Another way of finding the chair transition state shall also be explored here. Starting from the same approximation to the transition state made up of the two allyl fragments that was used for the previous optimisation, the distances between the pairs of terminal carbons were fixed to be unchanging during the next optimisation using the redundant coordinate editor in GaussView. After a "normal" optimisation (i.e. looking for a minimum on the potential energy surface) whilst respecting this fixed bond length (by using Opt=ModRedundant as a keyword) the hydrogens had slightly moved out of the plane they had been sitting in originally, away from the other fragment (logfile, ), but the distance between the terminal carbons had remained exactly at its value, as if there were a completely rigid bond of unchangeable length. So everything about the molecule was optimised, except along these two "bonds". Hence, before the next optimisation, this restriction was removed and the molecule was optimised to transition state using the TS(Berny) method as above however with the difference that the optimisation only took place along the path of these "bonds", i.e. the path of the reaction co-ordinate. The resulting structure (logfile) barely differed from the one found using the force constant method, as can be seen form selected parameters shown in the table below:
| property | force constant method | redundant coordinate method |
|---|---|---|
| terminal carbon bond length | 2.020 Å | 2.021 Å |
| point group | C2h | C2h |
| Energy (HF/3-21G) / Hartree | -231.6193 | -231.6193 |
| Imaginary frequency /cm-1 | -818.1 | -817.9 |
| Jmol |
Modelling the boat transition state using QST2
This third method of finding a transition state requires even less input in terms of knowledge about what the transition state looks like, one only has to input the reactant and product and map the atoms (i.e. tell the program which atom ends up where going from reactant to product), while Gaussian will try to find the lowest energy path between the two structures by interpolation.
The fourth conformer of 1 found above (Ci symmetry, anti2) was used both as a reactant and product, though the numbering of the atoms had to be changed for the product so that Gaussian would have to "break" the 3C-4C bond and form one between 1C and 6C by moving the atoms. This was done by having the reactant and the product in the same MolGroup in GaussView and using the Atom List interface.
Then optimising to transition state using the "TS(QST2)" method with the HF/3-21G basis set, Gaussian failed and returned a transition state that was not quite right as had been anticipated in the question. Following the manual alterations to the reactant and product suggested there and re-running the optimisation, a valid transition state was found with an imaginary vibrational frequency of -840 cm-1 corresponding to the reaction (logfile, ). The point group of this boat transition state is C2v, the distance between the bond forming/bond breaking carbons is 2.14 Å, and the energy was found to be -231.6028 Hartree (using HF/3-21G). The energy being significantly higher than for the chair transition state, we can conclude that the reaction it is much less likely to occur via this path.
IRC - Intrinisic Reaction Coordinate: finding the reaction path
The IRC method is used to find which conformation of a reactant will transform into the given transition state, and in which conformation of the product the transition state will end up in. The method starts from the transition state and analyses the the force constants. It modifies the geometry, step by step, in the direction of smallest potential energy by moving down from the saddle point (i.e. the transition state on the potential energy surface) in the direction of the steepest gradient as found from the force constants.
To simplify the calculation, one can instruct Gaussian to calculate the force constants only at the beginning, assuming that they will not change by much as we progress through the steps, and one can also limit the number of iterations (steps) in case Gaussian does not find a minimum.
Following the suggestion from the question, an IRC calculation starting from the chair transition state with the force constants calculated only once in the beginning and limited to 50 steps was initiated, calculating only in the forward direction (because our reaction happens to be symmetric). The calculation however did not reach a minimum, so three possible ways to continue were considered (in order of increasing computational expense): Either just optimising the final structure after 50 steps and hoping to end up in the right minimum, or re-running the calculation for more steps, but still without recalculating the force constants at each step, or else re-running the calculation but with calculation of the force constants after each step.
The second option was chosen and the maximum number of steps set to 100, but Gaussian still had not found a minimum (logfile F_4), so instead the third and most precise method was chosen, and with the help of the SCAN cluster it was found in only 3.5 minutes that after 46 steps (with recalculating the force constants after every step) Gaussian did find a minimum: the 2nd conformation of 1 found above (logfile). The Jmol applets below visualise the reaction path for both transition states using the data from the logfiles.
| Geometry of the Cope rearrangement | |||||
|---|---|---|---|---|---|
| via chair transition state | via boat transition state | ||||
The logfile for the boat transition state was also calculated using the scan (recalculating the force constants after each step), it took one step longer to find a minimum, and though this minimum is unstable (it has a synperiplanar configuration along the 3C-4C bond) it was not optimised further here, since it can be seen that a rotation of 60° about the 3C-4C bond would give the Conformation 3 of 1 (gauche 3) from above.
Activation energy
Now we are ready to calculate the activation energies for the different paths. This is in essence the difference in energy between the reactant and the transition state. As the reactant the conformation that was determined as the product/reactant using IRC for each transition state was used.
| Energy of Reactant/Product | Energy of Transition State | E‡ Activation Energy | ||||
|---|---|---|---|---|---|---|
| Hartree | Hartree | Hartree | kJ/mol | kcal/mol | ||
| Conformation 2 (gauche2) via CHAIR transition state | HF/3-21G | -231.69167 | -231.61932 | 0.0724 | 190 | 45.4 |
| RB3LYP/6-31G(d) | -234.61069 | -234.55698 | 0.0537 | 141 | 33.7 | |
| Experimental | 0.0534 (±0.0008) | 140 (±2) | 33.5 (±0.5) | |||
| Conformation 3 (gauche3) via BOAT transition state | HF/3-21G | -231.69266 | -231.60280 | 0.0899 | 236 | 56.4 |
| RB3LYP/6-31G(d) | -234.52133 | -234.54309 | 0.0682 | 179 | 42.8 | |
| Experimental | 0.0712 (±0.0032) | 187 (±8) | 44.7 (±2.0) | |||
As we can see, the energies determined with RB3LYP/6-31G(d) are much closer to the experimental value than those found with the faster HF/3-21G parameters, the calculated energies are just within experimental error. However, the geometries initially determined with the HF/3-21G basis set are barely different from those found with the RB3LYP/6-31G(d) method, as was seen above for Conformation 4 (anti2). This shows us that it is best to first map out the potential energy surface using a lower-level calculation method to find the relevant geometries, and only then applying the more sophisticated but computationally demanding methods to get good numerical values for the quantities of interest.
Part two: the Diels-Alder cycloaddition
| Ethene | Butadiene | Transition state | ||||||
|---|---|---|---|---|---|---|---|---|
| ethene logfile | cis-butadiene logfile | transition state logfile |
Method for finding the transition state:
- The two inital molecules optimised using AM1.
- Two initial molecules aligned as a guess.
- Then fix bonds to ca. 2.2 Å using redundant coordinate editor.
- Optimised using AM1 but with Opt=ModRedundant keyword.
- Gaussian, using AM1, did 13 steps of optimisation.
- New structure opened and redundant coordinate editor used to set the forming bonds to "derivative"
- Optimisation to TS (Berny) using Opt=ModRedundant
- Gaussian crashed after 6 steps.
- 6th step looked very much like a good TS, so used this geometry and optimised it to TS without using ModRedundant as a keyword.
- Gaussian terminated successfully after 1 step. The resulting structure has an imaginary vibrational frequency of -956 cm-1 that corresponds to the concerted forming of the two bonds in question.
(*) Illustrate the vibration that corresponds to the reaction path at the transition state. Is the formation of the two bonds synchronous or asynchronous?
The formation is synchronous, i.e. at the same time, i.e. concerted, as can be seen from the vibration.
(*) Is the HOMO at the transition structure s or a?
It is anti-symmetric, i.e. a with respect to the plane.
(*) Which MOs of butadiene and ethylene have been used to form this MO? Explain why the reaction is allowed.
It has been made from the LUMO of Ethene (which is a) and the HOMO of butadiene (which is also a).
Two orbitals of same symmetry ONLY can combine to give two new molecular orbitals (otherwise the reaction is not allowed). One of these new molecular orbitals is the transition state HOMO.