Rep:Mod3:BMWWiki
Benjamin Wild Wiki, Module 3
To view frequency vibrations, please click on the highlighted frequencies.
Cope Rearrangement Tutorial
Introduction

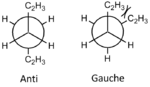
This experiment aims to find the lowest energy (most stable) conformer of 1,5-hexadiene in order to determine the mechanism in which the Cope rearrangement undergoes in its [3,3]-sigmatropic rearrangement (shown to the right). This rearrangement is an example of a peri-cyclic reaction, where a peri-cyclic reaction is one in which bonds ar broken or in a concerted cyclic transition state[1]. In studying the Cope rearrangement, it will be possible to confirm the concerted approach of pericyclic reactions.
Optimizing the reactants and products
| Conformer | Structure | Point Group | Energy/ a.u. | Relative Energy kcalmol-1 |
Stability Rank |
|---|---|---|---|---|---|
| anti 1 | 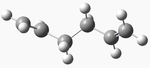 |
C2 | -231.69260 | 0.038 | 2 |
| anti 2 | 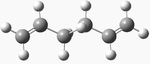 |
Ci | -231.69254 | 0.075 | 3 |
| anti 3 |  |
C2h | -231.68907 | 2.253 | 9 |
| anti 4 |  |
C1 | -231.69097 | 1.060 | 6 |
| gauche 1 |  |
C2 | -231.68772 | 3.100 | 10 |
| gauche 2 | 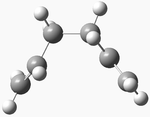 |
C2 | -231.69167 | 0.621 | 4 |
| gauche 3 | 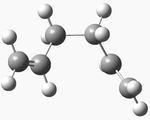 |
C1 | -231.69266 | 0.000 | 1 |
| gauche 4 |  |
C2 | -231.69153 | 0.709 | 5 |
| gauche 5 | 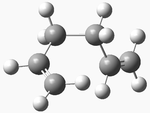 |
C1 | -231.68962 | 1.908 | 7 |
| gauche 6 |  |
C1 | -231.68916 | 2.196 | 8 |
Hatree Fock is a basic method that neglects electron correlation to provide a faster and less computationally expensive method in comparison DFT, for example. This technique was used to optimise the configurations of the different possible conformations of 1,5-heaxdienem shown in the table to the left. All of these results match closely those provided in the appendix attached to the lab wiki. One would expect to see one of the anti- configurations (because there would be less steric clash between the R groups) as the most stable, however using this initial optimisation technique, gauche 3 is seen to be the most stable (lowest in energy). It can be seen that anti 1 and anti 2 are very close in energy to gauche 3, and so I will look into further optimisation techniques which provide a more rigorous optimisation to see if gauche 3 truly is more stable, or if an anti conformer is. Below is a table of the re-optimised conformers using a DFT B3LYP/6-31G* method and basis set.
| Conformer | Structure | Point Group | Energy/ a.u. | Relative Energy kcalmol-1 |
Stability Rank |
|---|---|---|---|---|---|
| anti 1 | C2 | -234.61178 | 0.000 | 1 | |
| anti 2 | Ci | -234.61171 | 0.044 | 2 | |
| gauche 3 | 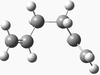 |
C1 | -234.61133 | 0.282 | 3 |
There seems to have been no real change in structures of the reoptimised conformers above, they have however become more stable than in the previous optimisation technique. There has however been a change in dihedral angles when looking at the terminal carbons. HF produces dihedral angles of 114.7° and DFT produces dihedral angles of 118.6°. Here we can also see that there is in fact quite a considerable difference between the gauche and anti conformers in terms of energy, with both anti forms coming out significantly lower in energy than the gauche form. There is a small difference in energy between anti 1 and anti 2, with anti 1 being the lower of the two, which shows that these are likely to interconvert under normal conditions. From these results, we can see that the Hartree Fock method of optimisation is of a much lower level, only providing a rough guide to the stabilities of different conformations.
IR analysis
Upon inspection of the low frequencies in each log file after completing the frequency optimisation, it could be seen that anti 2 and gauche 3 were the most likely to have converged (both have negative frequencies no larger than -10), whereas anti 1 appears to have not fully converged (negative frequencies more than -10). I wish to look at the most stable conformer, and seeing as anti 2 appears to have converged, and anti 1 not, I will look into this.
Looking at the vibrations in GaussView, it can be seen that there are 42 distinguished molecular vibrations (all positive). Below is the IR spectrum produced for the anti 2 conformer.

Below are the thermochemistry results for anti 2 taken from the frequency log table.
Zero-point correction= 0.142507 (Hartree/Particle) Thermal correction to Energy= 0.149853 Thermal correction to Enthalpy= 0.150797 Thermal correction to Gibbs Free Energy= 0.110933 Sum of electronic and zero-point Energies= -234.469204 Sum of electronic and thermal Energies= -234.461857 Sum of electronic and thermal Enthalpies= -234.460913 Sum of electronic and thermal Free Energies= -234.500777
Recalculated at 0K[2]:
Zero-point correction= 0.142944 (Hartree/Particle) Thermal correction to Energy= 0.142944 Thermal correction to Enthalpy= 0.142944 Thermal correction to Gibbs Free Energy= 0.142944 Sum of electronic and zero-point Energies= -234.468766 Sum of electronic and thermal Energies= -234.468766 Sum of electronic and thermal Enthalpies= -234.468766 Sum of electronic and thermal Free Energies= -234.468766
Optimizing the "Chair" and "Boat" transition structures
Chair conformation
Transition state optimisation[3]
There is an imaginary vibration at -817.89 cm-1 which is representative of the chair transition state. The terminal C-C bond distances between the separate allyl fragments are 2.02061Å and 2.02054Å respectively.
Transition state optimisation using frozen coordinates[4]
Optimising the transition state using frozen coordinates (initially set at 2.2Å), resulted in a transition state that appeared very close to that of the previous optimisation, however the C-C bond lengths between terminal carbons of the allyl groups reduced to 2.01931 and 2.01918 respectively.
Intrinsic reaction coordinate
Force constant always, maxpoints=50.
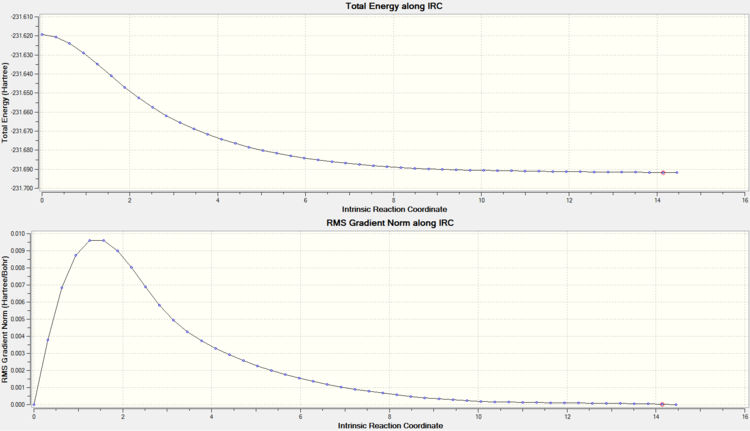
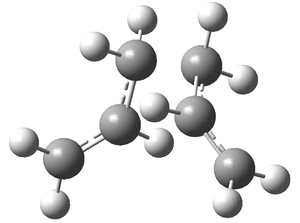
It can be seen that this optimised chair conformation closely matches the Gauche 2 conformation from before (-231.69167 a.u.). Force constant always and maxpoints=50 were used to ensure that there was convergence to a product (force constant always is the most reliable way of finding a minimum geometry).
Boat conformation
Transition state optimisation
Optimising the transition state initially with the QST2 TS optimisation method, failed to produce an optimised structure:
By preoptimising the structures before sending them to the Imperial SCAN service using the same method as before, a fully optimised transition state structure was obtained:
Looking at the IR vibrations there is a reported imaginary frequency at -839.95 cm-1, which represents the boat transition state formation. Here it can clearly be seen that sigma bonds are forming and breaking between terminal ends of the molecule (represented by the lengthening and contracting of bonds).
Optimising the transition state with the QST3 TS optimisation method, produced an optimisation state which clearly shows the breaking and formation of bonds (long bond means breaking, close carbon atoms mean bonding):
Intrinsic reaction coordinate
Force constant always, maxpoints=50.
It can be seen that this optimised chair conformation closely matches the Gauche 3 conformation from before (-231.69266 a.u.).
Activation Energies
| Hartree Fock 3-21G Chair Electronic Energy |
Hartree Fock 3-21G Boat Electronic Energy |
DFT/B3LYP 6-31G* Chair Electronic Energy |
DFT/B3LYP 6-31G* Boat Electronic Energy |
Hartree Fock 3-21G Chair 0K |
Hartree Fock 3-21G Boat 0K |
DFT/B3LYP 6-31G* Chair 0K |
DFT/B3LYP 6-31G* Boat 0K |
Hartree Fock 3-21G Chair 298.15K |
Hartree Fock 3-21G Boat 298.15K |
DFT/B3LYP 6-31G* Chair 298.15K |
DFT/B3LYP 6-31G* Boat 298.15K | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Transition state energy/a.u. |
-231.61932 | -231.60280 | -234.55698 | -234.54309 | -231.46669 | -234.41493 | -231.46133 | -231.44530 | -234.40901 | -234.39601 | ||
| Activation energy/a.u. (Anti 1 E - TS E) |
0.07328 | 0.08980 | 0.05480 | 0.06869 | 0.07291 | 0.05198 | 0.07131 | 0.08734 | 0.05297 | 0.06597 | ||
| Activation energy/a.u. (Anti 2 E - TS E) |
0.07322 | 0.08974 | 0.05473 | 0.06862 | 0.07285 | 0.05384 | 0.07124 | 0.08727 | 0.05285 | 0.06585 | ||
| Activation energy/kcalmol-1 (Anti 1 E - TS E) |
45.98 | 56.35 | 34.39 | 43.10 | 45.75 | 32.62 | 44.75 | 54.81 | 33.24 | 41.40 | ||
| Activation energy/kcalmol-1 (Anti 2 E - TS E) |
45.95 | 56.31 | 34.34 | 43.06 | 45.71 | 33.79 | 44.70 | 54.76 | 33.16 | 41.32 |
The values to the left calculated for 298K and electronic energies show a relatively good correlation with the experimental values (33.5±0.5 kcalmol-1 for chair TS, 44.7 ± 2.0 kcalmol-1 for boat TS). I have included both the activation energy with respect to anti 1 and anti 2 because anti 1 was found to be the true lowest energy conformer, however we have been using anti 2 for most other calculations and there is a small energy barrier between the two. The activation energies for 298.15K are values taken from the thermochemistry section in the log files for optimised anti1/ anti2/ chair/ boat. There is conformity between each method and temperature showing that the chair is more stable than the boat transition structure, and further confirms this as the transition state. The reason for the preference of the chair conformation for the transition state over the boat conformation is due an increased level of torsional strain in the latter, raising the energy. The values at 298.15K are also lower than at 0K, as to be expected, as less energy needs to be pushed into the reaction for it to proceed to the transition state.
Diels Alder Cycloaddition
cis-butadiene and ethylene

The HOMO visualisation for cis-butadiene shows anti-symmetry in both vertical and horizontal planes, whereas the LUMO visualisation shows symmetry in the vertical plane, and anti-symmetry in the horizontal plane. The HOMO visualisation for ethylene shows symmetry in both the horizontal and vertical planes, whereas the LUMO shows anti-symmetry in both planes.
Cycloaddition
|
After spending much time reoptimising the positioning of the ethylene group to allow for an sp3 entry of attack, I decided to use the redundant coordinate editor to preoptimise the positioning of the two groups (2.2Å frozen distance, 109.5° frozen angle). This was then optimised to a minimum using a semi-empirical/AM1 method, then optimised to a transition state (berny) using the same method. Below is an interactive graphic of the optimised transition state.
An imaginary frequency produced at -956.77 cm-1 shows the reaction proceeding via a [4π+2π] syn-cycloaddition. The motion of the computed vibration here shows both bonds forming simultaneously (synchronous), therefore confirming the theory which states that the reaction proceeds in a concerted fashion. Below are the HOMO and LUMO states of the transition state. The next lowest frequency at 146.84 shows an asynchronous bond formation, corresponding to a cyclisation which is higher in energy than the cycloaddition (bond forming and breaking do not occur at the same time.
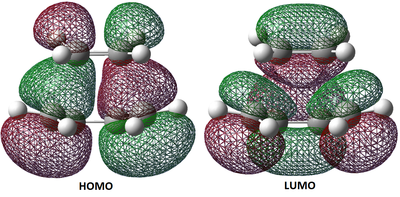
From this we can see that the overlaps to form the HOMO and LUMO orbitals in the transition state are combinations of orbitals from the individual molecules. The HOMO state can be considered as the overlap of the HOMO cyclobutadiene orbitals and the LUMO ethylene orbitals. The LUMO state can be considered as the overlap of the LUMO cyclobutadiene orbitals and the HOMO ethylene orbitals. With the LUMO's energy value being so close to zero (0.02315), it can be seen as non-bonding. Due to the symmetry and orientation of orbitals, this is an allowed combination of orbitals, and is why a more diffuse region of electrons density can be seen between the two molecules in the HOMO. We can see that there has been retention of symmetry (and asymmetry) from the original molecules to the optimised states above, therefore the HOMO is antisymmetric, and the LUMO is symmetric.
The distance between terminal carbons in the bonding process described have a distance of 2.12Å. All formal double bonds have a C-C distance of 1.38Å, and the C-C single bond in butadiene is 1.40Å. Literature[5] states typical sp3-sp3 C-C to be 1.54Å and sp2-sp2 C-C to be 1.33Å. This shows us that the double bonds are slightly longer than average (due to π electrons leaving to form a new bond), and the C-C single bond is shorter (due to it starting to form a double bond). The ethylene group is still too far away to be fully bonding (it is significantly longer than both the double and single bonds of butadiene). The tranistion state (along with the vibration) show an sp3 bond forming between the sp2 centres.
It is interesting to note the key features in the above MO diagrams. The HOMO shows donation of π electrons from cis-butadiene to the π* orbital of ethylene to form the two σ bonds, and the LUMO shows donation of π electrons from ethylene to the π* orbital of cis-butadiene to form a double bond in the C-C central bond.
Study of regioselectivity of the diels alder reaction
| Endo[6] | Exo[7] | ||||||
|---|---|---|---|---|---|---|---|
|
|
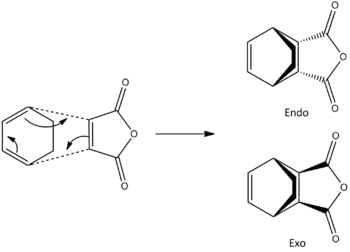
Using bond freezing techniques again, it was possible to generate the intermediates for both the endo and exo products (right) of the diels alder reaction. Each have negative frequencies, clearly showing concerted diels alder reactions. The endo product has its negative "imaginary" frequency at -806.38 cm-1, and the exo product has its negative "imaginary" frequency at -812.25 cm-1.
| Attribute | Endo | Exo |
|---|---|---|
| LUMO |  -0.036 |
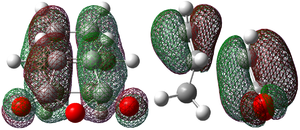 -0.040 |
| HOMO | 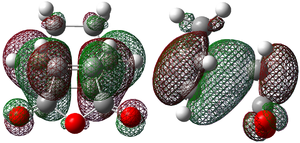 -0.345 |
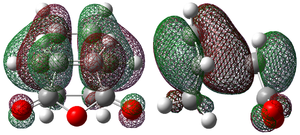 -0.343 |
| Terminal C-C bond length/Å |
2.16 | 2.17 |
| LUMO+1 |  -0.020 |
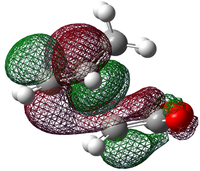 -0.020 |
| Qualitative diagram of secondary overlap[8] |
 |
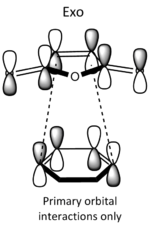 |
Each of the HOMO and LUMO orbitals for endo and exo show antisymmetry in the vertical axes, and no symmetry in the horizontal axes. The areas around the oxygen atoms have large nodes, which seem to be pushing electron density towards the C=C, to favour electron donation to form bonds with the cyclohexadiene. The LUMO+1 shows a larger electron density area in the endo product than in the exo product, implying that there is a larger contribution which can be attributed to the secondary orbital overlap.
IRC
| Endo | Exo |
|---|---|
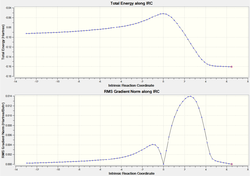 |
 |
 |
 |
It can be seen from the above graph showing the energies of the reaction pathway as the reaction proceeds (produced using IRC) that the exo conformer is initially lower in energy as the reactants, however at the transition state, the endo is slightly lower in energy (and both show an exothermic reaction overall). This is due to the kinetic control of the reaction, and confirms the stability of endo stated in the report guidelines. The below table provides further conformation of this.
Activation energy
| Endo | Exo | |
|---|---|---|
| Activation energy/a.u. | 0.04322 | 0.04536 |
| Activation energy/kcalmol-1 | 27.12 | 28.46 |
It can be seen from the table (left) that endo is kinetically more favoured. This is due to secondary orbital interactions, which cause there to be a greater overlap of orbitals to create a more stable transition state. IRC also shows endo to be the most thermodynamically stable product, when exo should be. This is likely to be due to the calculation method and basis set used not being overly accurate. If there were fewer time constraints, and if the SCAN service was working, I would use a higher method and basis set (e.g. DFT/B3LYP 631G*). Another possible reason for the endo and exo being the wrong way around for their final energies could be due to the calculation neglecting steric clashing. The endo product is likely to have a greater steric clash between the in coming maleic anhydride group and the π electron clouds in the cyclohexadiene. This issue may again be resolved by using a higher method and basis set.
Conclusion
This module has looked into different methods for optimisation of transition state structures. We used HF/3-21G, Semi-Empirical/AM1 and DFT/6-31G, whose accuracies and reliabilities increase in that order. To confirm that a transition state had indeed been found, IR frequencies were looked into to search for "imaginary" frequencies. IRC plots were produced to show the energy profile as the reaction moves from products to reactants via a transitions state, explaining the preference for a particular product or transition state.
Once a good grounding of different methods and techniques had been gained by looking into the cope rearrangement of the first section, it was possible to look into a more complex reaction system. The diels alder reaction of cyclohexadiene with maleic anhydride provide a more complex system to look into. The aim was to find a reason for the preference of the endo product over the exo product, knowing the reaction is kinetically controlled. This is explained in the above section (mainly down to secondary orbital overlap).
References
- ↑ H. Rzepa, Pericylic reactions http://www.ch.ic.ac.uk/local/organic/pericyclic
- ↑ https://wiki.ch.ic.ac.uk/wiki/images/d/da/0K_AGAIN.LOG
- ↑ DOI:http://hdl.handle.net/10042/to-10130
- ↑ DOI:http://hdl.handle.net/10042/to-10132
- ↑ R. Dias, Organic Chemistry, http://www.odu.edu/~rfdias/chem311/02BONDING.pdf
- ↑ DOI:http://hdl.handle.net/10042/to-10220
- ↑ DOI:http://hdl.handle.net/10042/to-10223
- ↑ Ian Fleming, Frontier orbitals and organic chemical reactions, John Wiley & Sons, 2006, 106-107





