Rep:Mod2clm08TC

Computational Analysis of BH₃

The structure of BH₃ was defined in Gaussview 3 and was optimised using the 3-21G basis set and a RB3LYP calculation method. The calculation was completed in 17 minutes and 56 seconds.

Vibrational Analysis

After optimisation the vibrational modes of the BH₃ were determined using a frequency calculation in gaussian. A description of the vibrations can be seen below.

Vibration Number	Form of Vibration	Frequency/ cm-1	Intensity	Symmetry Point Group (D3h)
1		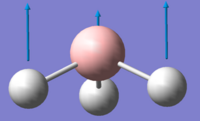1145.71	92.7	A"2
2		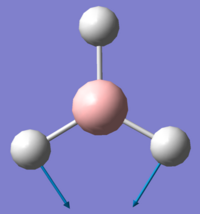1204.66	12.38	E'
3		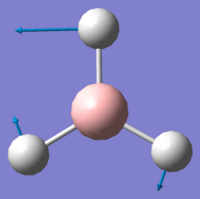1204.66	12.38	E'
4		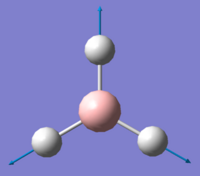2592.79	0	A'
5		2731.31	103.84	E'
6		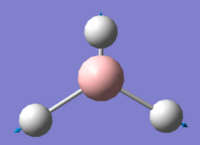2731.31	103.84	E'

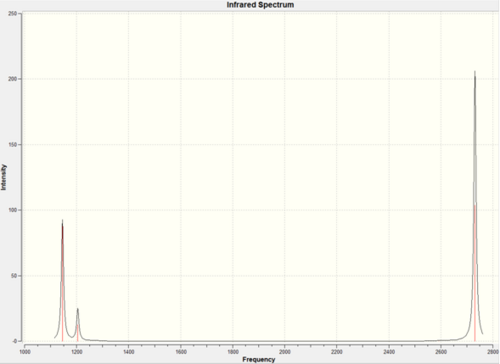
Using 3N-6 to determine the vibrational degrees of freedom 6 peaks are expected to be observed in the IR Spectrum as (3 x 4) - 6 = 6, however this is not the case and can be explained by by examining the calculated vibrations. As can be seen there are two sets of degenerate vibrations this means that only one peak is observed for two vibrations instead of two. The degenerate vibrations have the symmetry label E', with vibrations 2 and 3, 5 and 6 occurring at the same energies. In the case of vibration four there is no peak as intensity is calculated as this vibration is inactive. This is due to the motion of H atoms stretching away from the central B atom, this results in the dipole vector equalling zero as the stretch and compressions of the B-H bonds cancel one another out. As a result the spectrum below is that which is observed showing 3 peaks:

MO Analysis

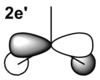
MO From LCAO Diagram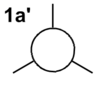
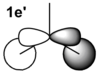
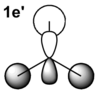
Calculated MO

From the table above it is clear that the orbitals depicted in the LCAO diagram are a very good representation of the molecular orbital surfaces for BH₃. Differences can be seen in the unoccupied orbitals which are much more diffuse than those shown in the MO diagram. This being the case MO theory is a very good approximation of the molecular orbitals, shown by the good correlation.

Structural Analysis of TlBr₃

TlBr₃ was defined on gaussview 3 and optimised (Media:TlBr3Opt.txt) using the LANL2DZ basis and a B3LYP calculation method, completed in 16 seconds. The symmetry of the molecule was fixed as D_3h so as expected the optimised molecule has Br-Tl-Br bond angles of 120^ο and a Tl-Br bond length of 2.65Å. The calculated bond length is very similar to the bond length determined for the crystalline structure of TlBr₃(OH₂)₂ as 2.62Å, this shows that the bond length calculated is a reasonable qualitative value. Summary of the optimisation is shown below:

TlBr3Opt
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	LADL2DZ
E(RB3LYP)	-91.21812851 a.u.
RMS Gradient Norm	0.00000090 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point group	D3H
Job cpu time: 0 days 0 hours 0 minutes 19.5 seconds

After optimisation a frequency analysis was undertaken using the same basis set and calculation method in order to maintain accuracy and to determine if the optimised molecule was a minimum in terms of total energy. As all of the vibrations for TlBr₃ were determined to be greater than zero it can be concluded that optimisation was successful. The low frequency vibrations show bending modes.

Frequency/ cm-1	Mode
46.43 (real mode)
46.43 (real mode)
52.14

Isomers of Mo(CO)₄L₂

In this case the cis and trans isomers of Mo(CO)₄L₂, where L=PCl₃, were defined in guassian and optimised initially using a LAN12MB basis set, and then with LAN12DZ basis. A frequency analysis of both isomers was then performed, all calculations used a B3LYP calculation method. After optimisation visualisation of the molecules appears to not to show bonds between the phosphorus and chlorine atoms this is due to the pre-set bond length limits for many bonds in gaussview. However this does not mean that the bond is not there, only that gaussview does not display it.

Note: What is a bond? A bond can be considered to be the interaction between two electron densities. A formal bond usually expressed with line (covalent) is the overlap of two electron densities to form a molecular orbital. In the case of an ionic bond we consider two charged species that are electro statically attracted to one another and are therefore bonded. This being the case a bond therefore is an attraction between atoms or molecules.

For the frequency analysis of both isomer please follow the links here: Cis-Mo(CO)₄(PCl₃)₂,Trans-Mo(CO)₄(PCl₃)₂

Examining the Cis-isomer it can be seen that the CO ligands adjacent to the PCl₃ ligands are bent away from the highly bulky phosphine ligands. This is a result of steric interactions between the bulky phosphines and the surrounding carbonyl ligands.

The very low frequencies of both isomers show bending of the P-Cl bonds and are as follows:

Cis-complex		Trans-complex
Frequency / cm-1	Vibration	Frequency / cm-1	Vibration
10.74		4.87
17.64		6.12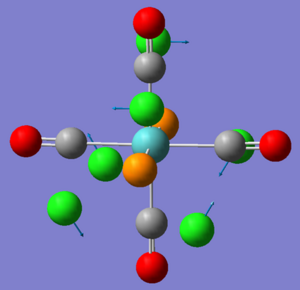

Examining the total energy of both complexes shows that the cis complex is the most stable as it has the most negative energy however there is very little energy difference between the two complexes (2.89 kJ mol^-1). The relative stability of the complexes can be explained by considering the effect of the PCl₃ ligand on the CO ligands and vice versa. The PCl₃ ligand is a good pi-donor ligand this increases the electron density on the metal centre, increasing back-bonding from the metal centre to the C=O ligands. In the trans-complex there are no C=O ligands trans to the phosphine ligands and therefore this effect is not seen however there are C=O ligands trans to the phosphine ligands so this effect becomes apparent, though not a large effect in this case it still lowers the total energy of the cis-complex slightly. This synergic bonding effect can be seen by examining the bond lengths between the two complexes.

Bond	Bond Length
	Cis-Complex		Trans-Complex
	Calc (L=PCl3)	Exp (L=PPh3)	Calc (L=PCl3)	Exp (L=PPh3)
Mo-P	2.51	2.58	2.44	2.50
Mo-C	2.06 (Cis-to-P)	2.04	2.11	2.01
	2.01 (Trans-to-P)	1.97 (Trans-to-P)
C=O	1.17 (Cis-to-P)	1.15	1.17	1.16
	1.18 (Trans-to-P)	1.14

As can be seen the Mo-C bond is shorter in the cis-complex, this shows that the there is a greater degree of back-bonding from the metal centre increasing the strength of the Mo-C bond. Analysing the stretching frequencies of the C=O ligands also supports these conclusions.

	C=O Stretch Frequency / cm-1
	Cis-complex		Trans-complex
	Calc (L=PCl3)	Exp (L=PPh3)	Calc (L=PCl3)	Exp (L=PPh3)
1	1945.43	1869.80	1950.52	1891.30
2	1948.93	1894.99	1951.15
3	1958.54	1923.33	1977.43
4	2023.53	2024.77	2031.21

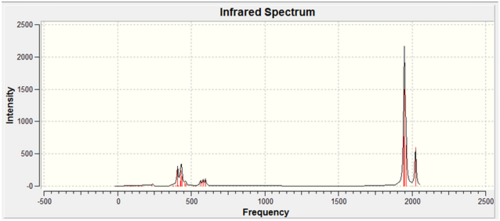
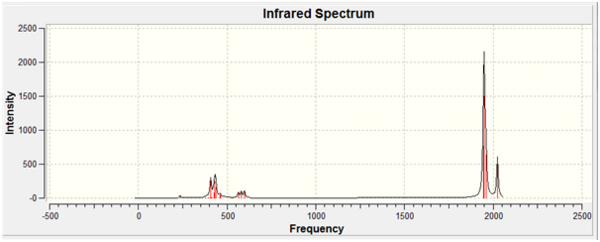
All of the calculated C=O stretching frequencies in the trans-complex require more energy, this indicates that the bonds are stronger and that synergic bonding is not in effect. From the table it can be seen that only one vibration is expected for the trans-isomer as it has D_4h symmetry, however it is apparent from calculations that four vibrations have been observed.

The IR spectra of both isomers:

Cis-isomer

Trans-isomer

Mini-Project

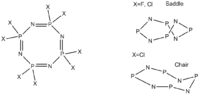
(NPX₂)₄ compound show interesting conformational preferences. In this section of the report I hope to identify why when X=F a saddle conformation is reported and when X=Cl both the chair conformation and the saddle conformation are reported. In order to do this the saddle and chair conformations of when X=F, CL will be defined optimised and analysed.

The chair conformer was defined in gaussview 3 and was fixed with C_2h symmetry. The (PCl₂N)₄ chair conformation was optimised using a B3LYP method and the 3-21G basis set [2] and the with the 6-311G d,p [3] basis set. A frequency analysis [4] was then completed, showing no negative frequencies indicating that the conformer is stable, followed by an MO analysis [5].

(PCl₂N)₄ Chair

Optimisation of the (PF₂N)₄ molecule into the chair conformation gave a planar structure[6]. In order to avoid optimisation to the planar structure some of the dihedral angles of the chair conformation were fixed using the Redundant coordinate Editor. This allowed for an initial optimisation of the molecule using the 3-21G basis set[7] and the B3LYP calculation method, this structure was further optimised using the 6-311G d,p basis set[8].

(PF₂N)₄ Planar

(PF₂N)₄ Chair

The definition of the saddle conformer was achieved by modifying the input file for the geometry of a P₄N₄, using the coordinates determined for the saddle conformation for an 8-membered ring in literature. This modification can also be made using gaussview by using the atom list editor. The relevant halides were added once the basic geometry had been modified.

The saddle (PCl₂N)₄ conformer was optimised initially using the 3-21G basis set [9] and a B3LYP calculation method. Optimising using a more accurate basis set yielded a boat-boat [10] conformation in order to optimise to a saddle conformation some of the dihedral angles within the initially optimised molecule were fixed using the Redundant Coordinate Editor in the edit drop down, the molecule was then optimised again using the 6-311G d,p basis set[11]. A frequency analysis was then completed[12], showing no negative frequencies indicating that the conformer is stable.

(PCl₂N)₄ Boat-Boat

(PCl₂N)₄ Saddle

The saddle conformer of (PF₂N)₄ was initially optimised using the 3-21G basis set and the B3LYP caculation method this returned a planar structure [13]. The dihedral angles of the molecule were then fixed and the molecule optimised using the 3-21G basis set [14]. The molecule was then optimised again using the 6-311G d,p basis set [15]. A frequency analysis was then completed[16], showing no negative frequencies indicating that the conformer is stable.

(PF₂N)₄ Saddle

MO analysis of the (PCl₂N)₄ chair conformation showed:

HOMO-4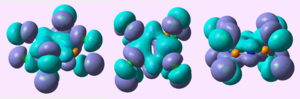
HOMO-3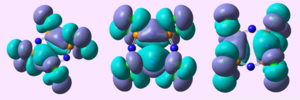
HOMO-2
HOMO-1
HOMO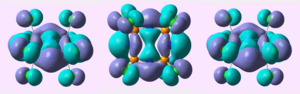
LUMO
LUMO+1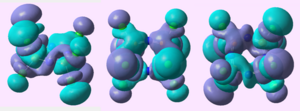

	(NPCl2)4			(NPF2)4
	Chair	Saddle	Boat-Boat	Chair	Saddle	Planar
Total Energy / kJ mol-1	-13827348	-13827349	-13827351	-6258730.3	-6258848.7	-6258847.9
P-N Bond Length / Å	1.58(p) 1.56(np)	1.57	1.58	1.60	1.56	1.56
P-X Bond Length / Å	2.05 2.04	2.04	2.04	1.56(eq) 1.57(ax)	1.57	1.57
P Mulliken Charge No.	1.054	1.045	1.046	1.354	1.411	1.413
N Mulliken Charge No.	-0.742(p)-0.767(np)	-0.75	-0.751	-0.795	-0.85	-0.798
X Mulliken Charge No.	-0.144(s) -0.155(l)	-0.147	-0.147	-0.292(eq) -0.304(ax)	-3.03	-3.03
X-P-X Angle / ο	102.9	103.2	103.2	98.8	99.6	99.4

Note: (ax=axial substituent), (eq=equatorial substituent), (p=in the same plane), (np=not in the same plane), (s=realted to shorter bond length), (l=related to longer bond length)

Though I have run out of time to analyse the results of all of the calculations I am now very familiar with the diversities of the gaussview programme. I understand now that much more human effort than just clicking some buttons is required to obtain the output that is desired.