Rep:Mod2:zy909
Structural Analysis of Thallium Tribromide
Theory
The geometry of thallium tribromide was optimised by density function theory (DFT) calculations, using the B3LYP (Becke three-parameter, Lee-Yang-Parr) hybrid functional and the LanL2DZ basis set.
Density functional theory is a quantum mechanical method for solving the Schrödinger equation, using functionals (functions of functions) of electron density. To get around the many-body problem of unsolvable equations for multiple interacting electrons, Kohn and Sham[1] introduced an approximation of the Schrödinger equation for non-interacting electrons, which may be solved easily by representing the wavefunction as a Slater determinant; this produces the same electron density as interacting systems. Within this formulation, the kinetic energy may be solved exactly, while the potential energy incorporates the external potential as well as exchange and correlation effects. Within this model, the exchange-correlation energy cannot be solved exactly and must be approximated.
Hybrid functionals[2] provide approximations for this exchange-correlation energy, and incorporate Hartree-Fock exchange energy as well as functionals for both the exchange energy and electron correlation. The B3LYP functional[3] is among the most popular in quantum chemistry, and is an empirically parametrised hybrid of Hartree-Fock exchange energy, Becke's 1998 exchange functional[4], the Vosko-Wilk-Nusair (VWN) functional[5] for local correlation, and and the Lee-Yang-Parr functional[6] for non-local correlation.
The LanL2DZ basis set used is suitable for systems with transition metal atoms up to bismuth, and uses a pseudo-potential for heavy atoms. For such atoms, most electrons are found in core electron orbitals and do not contribute to bonding, and may therefore be approximated with a simple pseudo-potential, while valence electrons are modelled as normal with Gaussian functionals. The Lan2LADZ basis set applies the Los Alamos Effective Core Potential (ECP) and a double-zeta basis set for elements Na-Bi, and the Dunning-Huzinaga valence double-zeta basis set for first-row elements. Double-zeta basis sets represent valence orbitals with two basis functions, each of which is composed of multiple Gaussian functions, and are used to give spatial flexibility to the electron density functional. For transition-metal complexes, more accurate results may be obtained by adding diffuse and polarisation functions[7], or by mixing basis sets to use all-electron basis sets (e.g. 6-31+G**) for non-transition metal atoms[8].
It is necessary to use the same method, basis set and parameters for each set of calculations (optimisation and frequency) as the potential energy surface is dependent on the parameters specified. An optimised geometry lying at a minimum on a potential energy surface may not also correspond to a minimum point on another potential energy surface calculated with a different set of parameters. In this situation, a non-optimal structure would input into a frequency calculation, resulting in incorrect or negative frequencies being obtained.
Structure Optimisation
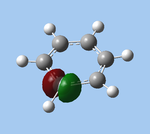
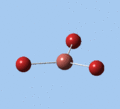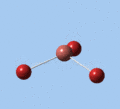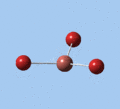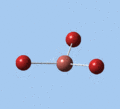
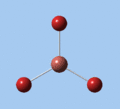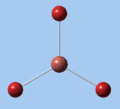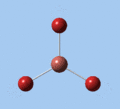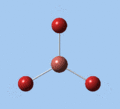
Thallium tribromide was optimised by B3LYP/LanL2DZ. Tight convergence criteria (opt=tight int=ultrafine) were then applied to further minimise the energy and reduce low frequencies in the frequency analysis. This lowers the with RMS force thresholds of 1×10-5 versus 3×10-4 and RMS displacement thresholds of 4×10-5 versus 1.2×10-3, which consequentially reduces the magnitude of low frequencies (discussed in Frequency Analysis), indicating a higher degree of accuracy.
| Method | E(RB3LYP) / a.u. | rTl-Br / Å | ∠Br-Tl-Br / ° |
|---|---|---|---|
| B3LYP/LanL2DZ | -91.21812851 | 2.65 | 120.0 |
| B3LYP/LanL2DZ (tight) | -91.21813024 | 2.65 | 120.0 |
| MP4 (non-relativistic)[9] | 2.524 | ||
| QCISD(T) (non-relativistic)[9] | 2.527 | ||
| Experimental (TlBr3.4H2O)[10] | 2.52 | 120.5 |
The DFT calculations yield a Tl-Br bond length that deviates significantly from the experimental value, although some differences are to expected in comparing gas-phase and X-ray crystal geometries. Nevertheless, a further comparison of the DFT model with the MP4 and QCISD(T) post-Hartree-Fock methods reveal the inadequacies of the DFT method at the level of theory used, and also show that electron correlation, which is modelled in the post-Hartree-Fock methods, is an important factor in describing the structure of thallium bromide.
Frequency Analysis

A frequency calculation is then performed to confirm that the structure has been optimised fully. As the vibrational frequency represents the second derivative of the potential energy surface (PES), an optimised structure, which lies on a local minimum on this PES, will have only positive vibrational frequencies. In contrast, transition states, which lie on PES maxima, have a single negative frequency corresponding to the reaction coordinate from starting material to product. Consequently, the presence of any negative frequencies would indicate that the structure has not been optimised completely.
In addition, polynuclear molecules with N atoms have 3N-6 vibrational modes. This is derived from the 3N degrees of freedom available to 3N atoms, less the 6 degrees of freedom (3 translational, 3 rotational) that are removed by bonding constraints - when N atoms are bonded in a molecule, translation (3 DoF) or rotation (3 DoF) about the center of mass do not affect the relative positions of atoms, and thus do not contribute to any vibrational frequencies. Gaussian calculates these frequencies, which are termed "low frequencies"; in ideal, well-optimised geometries, these frequencies should be zero. As such, any significant low frequencies obtained are indicative of improperly optimised structures.
| Method | Component | Low frequencies | E’ | A2” | A1’ | E’ | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| B3LYP/LanL2DZ SPECTRa | Frequency / cm-1 | -3 | 0 | 0 | 0 | 4 | 4 | 46 | 52 | 165 | 211 |
| Intensity | 4 | 6 | 0 | 25 | |||||||
| B3LYP/3-21G (tight) SPECTRa | Frequency / cm-1 | 0 | 0 | 0 | 2 | 3 | 3 | 47 | 52 | 165 | 211 |
| Intensity | 4 | 6 | 0 | 25 | |||||||
| MP2[9] | Frequency / cm-1 | 55 | 66 | 197 | 233 | ||||||
| Intensity | 5 | 5 | 0 | 36 | |||||||
| Experimental (EtOH solution)[11] |
Frequency / cm-1 | 51 | 125 | 190 | 220 | ||||||
Optimisation with tight convergence criteria reduces the magnitude of low frequencies and eliminates the negative frequencies, implying that the structure is more accurate, although the calculated frequencies do not differ significantly. As the largest low frequency is more than one order of magnitude smaller than the lowest vibrational frequency, it may be concluded that the geometry is sufficient optimal.
The frequencies and intensities calculated by DFT match those obtained by MP2 (post-Hartree-Fock) relatively well, with 10-20% deviations, but differ from the experimentally observed frequencies, especially for the A2” mode. This deviation can probably be attributed to the fact that the computed frequencies are based on gas-phase models, while the experimental absorption spectrum was obtained from ethanolic solutions of TlBr3.
The A1’ vibrational mode is infrared-inactive because the symmetric Tl-Br stretch does not produce a change in net dipole moment, which is necessary for the vibrational mode to interact with incoming electromagnetic radiation - no infrared absorption is therefore associated with this frequency.
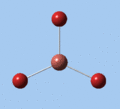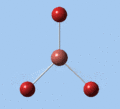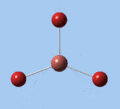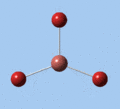
|
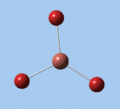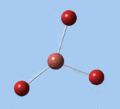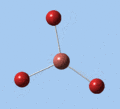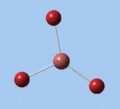
|
|
|

|
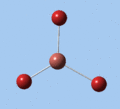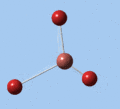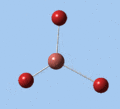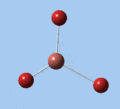
|
| E' | E' | A2 | A1' | E' | E' |
Molecular Orbital Analysis of Borane
Structure Optimisation
Borane was optimised by DFT calculations, using the B3LYP hybird functional and 3-21G basis set. The obtained geometry is shown in the table below, and compared with calculations at high-level theory (CCSD(T)/aug-cc-pVTZ), as well as experimental data.
| rB-H / Å | ∠H-B-H / ° | |
|---|---|---|
| B3LYP/3-21G | 1.19 ± 0.01 | 120.0 ± 0.1 |
| CCSD(T)/aug-cc-pVTZ[12] | 1.19 | 120.0 |
| Experimental[13] | 1.185 | 120.0[14] |
The close match with both experimental results and high-level CCSD(T)/aug-cc-pVTZ calculations demonstrate that the geometry optimisation is sufficiently accurate. For small molecules like borane with first and second period atoms only, the low-level 3-21G basis set is sufficient to give accurate results - in any case, further improvement in accuracy might lie within the error of the calculations.
Frequency Analysis
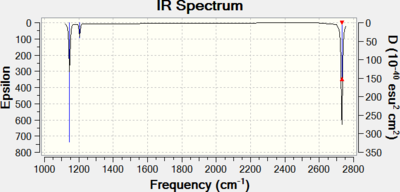
Upon performing the frequency analysis on the borane geometry obtained without tight convergence criteria, three negative low frequencies were found, indicating that the geometry was incompletely optimised. The borane geometry was then further optimised (opt=tight int=ultrafine), upon which the largest magnitude of low frequencies was lowered from 67 to 16. As the largest low frequency is almost two orders of magnitude smaller than the smallest vibrational frequency, the optimisation is deemed to sufficient.
There was a negligible difference of 0.001Å in bond length, within calculation error, between the original and tight structures, and no difference in the calculated bond angle of 120°.
| Method | E(B3LYP) / a.u. | Component | Low frequencies | A2" | E' | E' | A1' | E' | E' | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B3LYP/3-21G SPECTRa | -26.46226338 | Frequency / cm-1 | -67 | -66 | -66 | 0 | 0 | 0 | 1144 | 1204 | 1204 | 2598 | 2737 | 2737 |
| Intensity | 93 | 12 | 12 | 0 | 104 | 104 | ||||||||
| B3LYP/3-21G (tight) SPECTRa | -26.46226384 | Frequency / cm-1 | -16 | -16 | -11 | 0 | 0 | 0 | 1145 | 1204 | 1204 | 2593 | 2731 | 2731 |
| Intensity | 93 | 12 | 12 | 0 | 104 | 104 | ||||||||
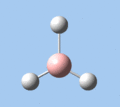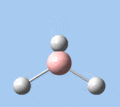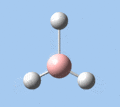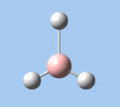
Of the 6 vibrational modes, the A1' mode (2593 cm-1) is infrared-inactive, as the symmetric B-H stretching does not change the dipole moment of the borane molecule. Without any change in dipole moment, this vibrational mode does not interact with electromagnetic radiation and therefore does not show a corresponding infrared absorption peak. The vibrational modes of greatest intensity are the A2" (B-H out-of-plane bend) and E' (B-H asymmetric stretch) absorptions, as these involve the largest changes in net dipole moment. In contrast, the E' (rocking and scissoring) modes involve only a slight change in dipole moment, and absorb weakly.
|
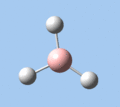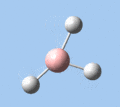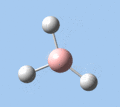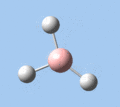
|

|
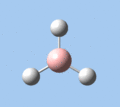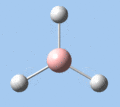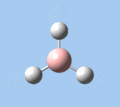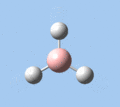
|
|
|
| A2 | E' | E' | A1' | E' | E' |
Molecular Orbitals
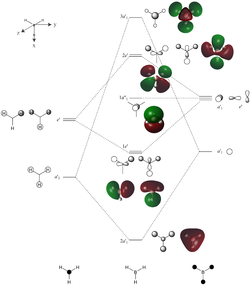
| Orbital | Energy / eV |
|---|---|
| 3a’1 | +0.192 |
| 2e’ | +0.189 |
| 1a”1 (LUMO) | -0.075 |
| 1e’ (HOMO) | -0.357 |
| 2a’1 | -0.518 |
| 1a’1 | -6.730 |
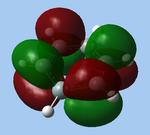
The computed molecular orbitals (MOs) closely match those given by a qualitative LCAO approach. As can be seen from the diagram to the right, both approaches give MOs that are similar in phase and shape. The computational approach is useful in this instance for visualising the diffuse nature of MOs, in contrast to the discrete atomic orbitals in the LCAO approach. Moreover, the computational approach allows for the quantification of orbital size, whereas atomic orbitals in LCAO are sized approximately based on atomic energies. Finally, while exact energies can be derived for each MO in the computational approach, and the MOs therefore ordered precisely, the LCAO method does not allow for this, and relative ordering must be guessed by chemical intuition based on atomic energies and the extent of through-bond and through-space interactions, both bonding and anti-bonding.
In the case of borane, the relative energies may be easily determined for the 2a’1, 1e’ and 1a”1 orbitals: 2a’1 is fully bonding and lowest in energy, 1e’ has one nodal plane and is slightly higher in energy, followed by 1a”1 which is non-bonding. The 2e’ and 3a’1 MOs are net anti-bonding in character, but their relative energies cannot be determined by LCAO. However, from the DFT calculations, 3a’1 (+0.192 eV) is higher in energy than 2e' (+0.189 eV), allowing them to be ordered in the MO diagram.
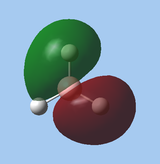
|

|

|

|
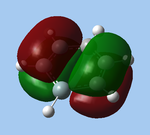
| HOMO (1e’) | LUMO (1a”1) |
Nevertheless, the most important orbitals are the HOMO (1e’) and LUMO (1a”1). For these orbitals, the qualitative LCAO approach is in good agreement with quantitative calculations, both in terms of MO shapes and relative energies. In this case, the LCAO approach indicates that the LUMO is centred at boron, and that it is non-bonding and therefore low in energy, supporting experimental evidence of borane acting as an electrophile / Lewis acid at boron; as its HOMO is even lower in energy, borane does not act as a nucleophile. The LCAO approach is therefore useful for quickly obtaining an approximate understanding of borane's reactivity, without resorting to quantitative calculations.
In summary, as there are no significant differences between the computed and LCAO MOs in the case of borane, it can be concluded that qualitative MO theory provides a simple and reasonably accurate way of understanding the bonding in simple molecules. However, LCAO analysis is not amenable to more larger, complicated molecules with no symmetry - for these, the computational method provides the most realistic picture of molecular bonding, especially for long-range through-space interactions that may be difficult to model with LCAO.
Cis-trans Isomerism
Introduction
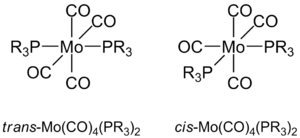
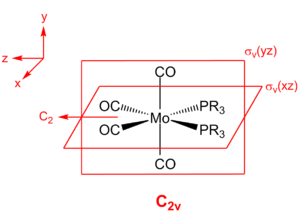
The octahedral molybdenum complex Mo(CO)4(PPh3)2 exists in two geometrically isomeric forms, the cis and trans forms which may be isolated; however, the cis isomer is found to equilibrate to the trans form under thermal conditions[15]. Furthermore, the isomers may be differentiated by infrared spectroscopy, as the number of allowed vibrational modes for the C-O stretch differs. The cis isomer has C2v symmetry, and has 4 C-O vibrational modes that are observed experimentally, while the trans isomer has a greater degree of symmetry (D4h), and only 1 C-O vibrational mode is observed in the infrared spectrum[15].
In this section, the two isomeric forms of the tetracarbonylmolybdenum complexes are studied computationally, using a model system with PCl3 ligands. Relative energies are calculated to test the accuracy of the DFT computational methods in predicting relative stabilities, and frequency calculations performed for comparison with experimental infrared spectra.
Structure Optimisation
| Method | Isomer | E(B3LYP) / a.u. | ΔEelec / kJ mol-1 |
G / a.u. | ΔG / kJ mol-1 |
|---|---|---|---|---|---|
| B3LYP/LanL2MB (loose) |
Trans | -617.52204988 | 8.0 | ||
| Cis | -617.52510215 | ||||
| B3LYP/LanL2DZ | Trans | -623.57603113 | 2.7 | -623.595116 | -1.5 |
| Cis | -623.57707196 | -623.594539 | |||
| B3LYP/LanL2DZ (extra d) |
Trans | -623.69415611 | -3.3 | -623.710500 | -8.3 |
| Cis | -623.69291233 | -623.707340 |
While Mo(CO)4(PPh3)2 is the compound of interest, modelling the triphenylphosphine ligands is computationally expensive and slow. To get around this limitation, the phenyl groups are approximated with chlorine atoms (R = Cl), which have similar electron-withdrawing properties.
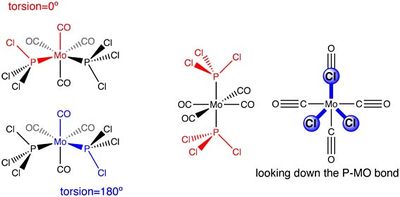
Both cis and trans isomers were first optimised using the B3LYP hybrid functional and minimal basis set LanL2MB, which uses a minimal basis (MB) set for valence electrons. Loose convergence criteria (opt=loose) were used to obtain rough geometries, which were noted to be missing the Mo-P and P-Cl bonds. The bonds were re-added to the structure, and the C-Mo-P-Cl dihedral angles adjusted as shown in the diagram, based on a prior exploration of the rotational profile[16]; geometries were then re-optimised using the larger LanL2DZ basis set, which uses a more accurate split-valence double-zeta (DZ) basis set to describe valence electrons. In addition, tight convergence criteria (opt=tight int=ultrafine scf=conver=9) were used to obtain the optimised geometries. This time, the Mo-P bonds were retained in the optimised geometry of the trans isomer, although the P-Cl distances found were still too long for Lewis bonding.
Subsequently, an additional d function was added to phosphorus, so as to improve modelling of its tendency to form hypervalent compounds using low-lying d orbitals[17]. Upon optimisation, the P-Cl bond distance was significantly reduced from 2.24 Å to 2.12 Å, much closer to the P-Cl bond length of 2.04 Å in PCl3. The following input was used for the d function:
P 0 D 1 1.0 0.55 0.100D+01 ****
As larger basis sets are used, the optimised energies gradually converge towards the actual ground-state energy, in line with the variational principle. Most significantly, the cis isomer is found to be more stable with smaller basis sets, but at the highest level of theory used, the trans isomer was calculated to be more stable, fitting experimental observations that trans-Mo(CO)4(PR3)2 complexes are more stable than the corresponding cis isomers[18]. The calculated energy difference of 8.3 kJ mol-1 corresponds to an equilibrium constant of 28 at 298K in favour of the trans isomer, indicating that thermal equilibration should convert the cis isomer into the trans form.
The trans isomer is the more stable form due to reduced steric repulsion between the phosphine ligands, as is evident from the geometrical distortions in the cis isomer (see Geometrical Analysis). The equilibrium could be shifted even further in favour of the trans isomer by using bulky phosphine ligands such as PPh3 and P(t-Bu)3[19]. To force cis coordination, bidentate phosphine ligands such as dppe (1,2-bis(diphenylphosphino)ethane)[20] may be used.
Geometry Analysis
| Compound | Method | rMo-P / Å | rP-R / Å | rMo-C / Å | rC-O / Å | ∠P-Mo-P | ∠R-P-R | θC-Mo-P-R / ° |
|---|---|---|---|---|---|---|---|---|
| trans-Mo(CO)4(PCl3)2 | B3LYP/LanL2MB (loose) | 2.48 | 2.40 | 2.11 | 1.19 | 180.0 | 97.6 | - |
| B3LYP/LanL2DZ | 2.44 | 2.24 | 2.06 | 1.17 | 177.4 | 99.3 | 0.0 | |
| B3LYP/LanL2DZ (extra d) | 2.42 | 2.12 | 2.06 | 1.17 | 176.7 | 100.1 | 0.0 | |
| trans-Mo(CO)4(PPh3)2 | Experimental[21] | 2.500 | 1.828 | 2.016 | 1.165 | 180.0 | - | - |
| cis-Mo(CO)4(PCl3)2 | B3LYP/LanL2MB (loose) | 2.53 | 2.41 | 2.06 | 1.19 | 94.7 | 97.4 | - |
| B3LYP/LanL2DZ | 2.51 | 2.24 | 2.01 | 1.18 | 94.2 | 99.5 | 6.5 | |
| B3LYP/LanL2DZ (extra d) | 2.48 | 2.12 | 2.02 | 1.18 | 94.3 | 100.1 | 7.0 | |
| cis-Mo(CO)4(PPh3)2 | Experimental[22] | 2.577 | 1.832 | 2.007 | 1.145 | 104.62 | 101.5 | - |
| PCl3 | Experimental[23] | 2.039 | 100.27 |
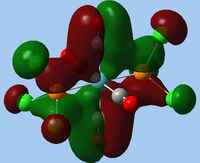
|
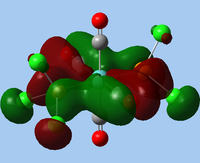
|
| MO 31 | MO 32 |
The bound PCl3 ligands are similar to gas-phase PCl3 in terms of bond angle, especially with larger basis sets. However, the P-Cl bond is lengthened upon binding to the metal centre, because electron donation from phosphorus to the metal decreases electron density in the P-Cl bonding orbitals, weakening the bond.
The trans isomer has shorter Mo-P bond distances than the cis isomer, which may be rationalised by steric factors in the cis isomer that prevent the PCl3 from approaching closer to the Mo centre[22]. Steric effects cause the P-Mo-P bond angle (94.3°) in the cis isomer to deviate from the ideal octahedral angle of 90°; this phenomenon is also observed with Mo(CO)4(PPh3)2 (∠P-Mo-P = 104.6°). The effects of steric strain in the cis isomer are also evident from the dihedral angle between the CO ligand and Cl atom, which should be fully eclipsed to maximise the stabilising interaction between the phosphorus p and Mo-C-O bond orbitals (see diagram). This is the case with the trans isomer, but not with the cis isomer, which deviates by 7° in order to minimise repulsive interactions between Cl atoms. These differences are significant as they are well outside the limits of calculation error, which is approximately 0.01Å for lengths and 0.1° for angles.
Additionally, in the most stable conformation of the cis isomer, the eclipsed P-Cl bonds bear a syn relationship with each other, whereas these are anti in the trans isomer, again to reduce repulsion between Cl atoms. A comparison of conformer energies shows that while both confomers of the trans isomer are essentially equivalent in energy, within the limits of calculation error, the syn conformer for the cis isomer does not actually lie on a minimum of the potential energy surface, and is approximately 7.3 kJ mol-1 higher in energy.
With bulkier phosphine ligands such as PPh3, this effect would be expected to be even more pronounced. Tolman's[24] cone angles for PPh3 (145°) and PCl3 (125°) show that the PPh3 ligand would be expected to have an even greater steric bulk than PCl3; this is supported by the larger R-P-R bond angle of bound PPh3 (101.5°) as compared to PCl3 (100.1°). Comparing the complexes with bound PPh3 and PCl3 ligands, the Mo-P bonds are found to lengthen in the PPh3 complexes; this effect was especially pronounced for the cis isomer, in line with expectations that the cis isomer is more sterically strained.
However, the extent of this deviation is less than in cis-Mo(CO)4(PPh3)2, where the greater steric strain between the bulky PPh3 ligands forces a lengthening of the Mo-P bond (2.577Å vs 2.48Å) and expansion of the P-Mo-P angle (101.5° vs 100.1°).
| Isomer | Conformer | E(B3LYP) / a.u. | ΔEelec / kJ mol-1 |
|---|---|---|---|
| Trans | Syn | -623.69415611 | -0.5 |
| Anti | -623.69396845 | ||
| Cis | Syn | -623.69013442 | 7.3 |
| Anti | -623.69291233 |
The Mo-C bonds are found to be longer in the trans isomer, which may be understood in terms of the Mo centre's back-bonding ability. In the trans isomer, the phosphine ligands are closer to the Mo atom and donate more electron density onto the metal centre, as demonstrated by a natural population analysis: the cis isomer is has a calculated natural charge of -2.275, while the trans isomer has a more negative charge of -2.344. In turn, the trans isomer exhibits a greater degree of back-bonding with its CO ligands, resulting in longer Mo-C and shorter C-O bond lengths.
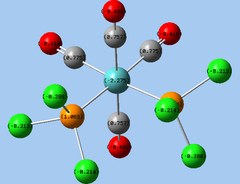
|

|
| Cis isomer | Trans isomer |
Bonding
In a quantum mechanical treatment of bonding, the traditional idea of localised bonding due to valence-bond theory is replaced by the delocalised bonding represented by molecular orbitals; molecules are not held together by discrete bonds between bonds, but by diffuse orbitals that may bond multiple atoms together. Nevertheless, the idea of chemical bonds in Lewis structures is still useful as an abstraction of the predominant bonding interactions in molecules. The output from ab initio DFT calculations may thus be represented graphically as atoms with localised bonds drawn in where atoms are within a certain threshold distance of each other. This is necessarily based on empirical data of typical bond lengths, as DFT models molecules based on electron density rather than discrete bonds. Consequently, in some instances, bonds may be missing from the final optimised structure, simply because the calculated bond lengths lie beyond the arbitrary limits defined. In these instances, chemical intuition must be used to interpret the final structure; the larger than usual bond distance may also indicate some sort of anomaly in the calculation or the molecule.
In the case of the Mo(CO)4(PCl3)2 isomers, the missing Mo-P and P-Cl bonds in the incompletely optimised structures were symptomatic of poorly optimised structures with larger-than-expected bond lengths. As the basis set was enlarged, the calculated bond lengths shortened and the bonds re-appeared in the graphical output, providing a rough indication of optimality in structure.
Frequency Analysis
The frequency calculations performed indicate that the structures obtained are sufficiently optimal. Adding an extra d function in the basis set caused the calculated CO stretching frequencies to converge slightly towards the experimental values, but did not greatly reduce the magnitude of low frequencies, which were already under ±10 cm-1.
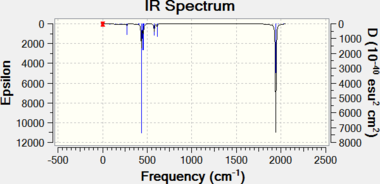
|
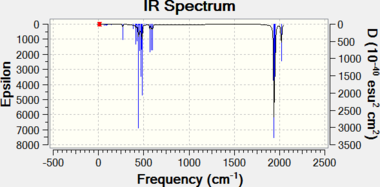
|
| Trans isomer | Cis isomer |
| Compound | Method | Component | Low frequencies (molecule translation & rotation) |
Mo-P rotational frequencies | CO stretching frequencies | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Trans isomers (D4h) | Eu | B1g | A1g | |||||||||||
| Trans-Mo(CO)4(PCl3)2 | B3LYP/LanL2DZ SPECTRa | Frequency / cm-1 | -2 | 0 | 0 | 0 | 0 | 3 | 5 | 6 | 1950 | 1951 | 1977 | 2031 |
| Intensity | 0 | 0 | 1475 | 1467 | 1 | 4 | ||||||||
| B3LYP/LanL2DZ (extra d) SPECTRa | Frequency / cm-1 | -2 | -2 | 0 | 0 | 0 | 3 | 5 | 7 | 1939 | 1940 | 1967 | 2025 | |
| Intensity | 0 | 0 | 1606 | 1606 | 6 | 5 | ||||||||
| Trans-Mo(CO)4(PPh3)2 | Experimental[15] | Frequency / cm-1 | 1901 | |||||||||||
| Cis isomers (C2v) | B2 | B1 | A1 | A1 | ||||||||||
| Cis-Mo(CO)4(PCl3)2 | B3LYP/LanL2DZ SPECTRa | Frequency / cm-1 | -2 | 0 | 0 | 0 | 1 | 2 | 11 | 18 | 1945 | 1949 | 1958 | 2023 |
| Intensity | 0 | 0 | 763 | 1498 | 633 | 598 | ||||||||
| B3LYP/LanL2DZ (extra d) SPECTRa | Frequency / cm-1 | -2 | -1 | 0 | 0 | 0 | 1 | 12 | 20 | 1939 | 1942 | 1953 | 2019 | |
| Intensity | 0 | 0 | 1597 | 821 | 592 | 541 | ||||||||
| Cis-Mo(CO)4(PPh3)2 | Experimental[15] | Frequency / cm-1 | 1897 | 1908 | 1927 | 2023 | ||||||||
Symmetry Considerations
Multiple low frequencies are observed for both cis and trans isomers of Mo(CO)4(PCl3)2. In particular, the two lowest normal frequencies correspond to conrotatory and disrotatory motion about the Mo-P bonds. At room temperature, the average thermal energy is RT, which corresponds to a wavenumber of 207 cm-1; these rotational frequencies are below 20 cm-1, indicating that rotation about those bonds is facile. Consequently, as the phosphine ligands are not static, the complexes gain a higher degree of symmetry, with the trans isomer taking on D4h symmetry (rather than C2v) and the cis isomer taking on C2v symmetry (rather than C2).

|
|
| Trans isomer | Cis isomer |
The key difference between simulations and reality here is that the DFT models consider the complexes as static molecules at the bottom of their potential energy well, which hence have lower symmetry, whereas the complexes would exist as a mixture of conformers in dynamic equilibrium. Infrared absorption does not take place on a fast-enough timescale to differentiate between conformers, so a time-average sample is observed with a consequential higher level of symmetry. Nevertheless, even though the DFT models ascribe the symmetry label A to all the C-O stretching vibrations, they have been correlated with the corresponding symmetry labels in ideal C2v (cis) and D4h (trans) point groups. This was performed by considering the symmetry representation of the C-O stretching vectors for each isomer, reducing this into the irreducible representations of the corresponding point groups, and then matching the irreducible representations to the vibrational modes identified.
Literature Comparison
The frequency calculations are found to agree well with the literature in terms of the number of infrared-active CO stretching absorptions - with the cis isomer, 4 absorptions are observed as predicted, while with the trans isomer, 1 single absorption is observed, matching the single degenerate set of Eu absorptions predicted.
With the trans isomer, minor deviations from ideality are nonetheless observed, with the Eu vibrational modes not completely degenerate, and non-zero intensities calculated for the B1g and A1g and vibrational modes. These occur because the trans isomer deviates from the actual D4h symmetry in the DFT model, as explained in the previous section. With the breaking of symmetry, the Eu modes become non-degenerate, while the B1g and A1g modes correspond to slight changes in net dipole moment and are no longer forbidden. Nevertheless, as the structural deviation from D4h symmetry is minor, the deviation in spectroscopic properties is similarly minute.
Substituent Effects on Silabenzene Reactivity (Mini-Project)
Introduction
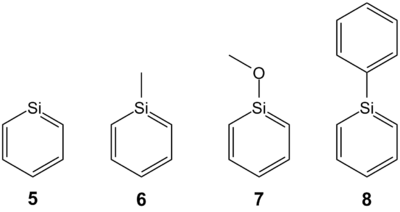
Silabenzene 5 and its derivatives, being the silicon analogues of benzene, expected to share similar properties of organic aromatic systems. However, these compounds have proven extremely difficult to synthesise in the laboratory, and the formation of simple silaaromatics has only been deduced by trapping with appropriate dienophiles[25] or with spectroscopic techniques[26]. The lower coordination number with Si multiple bonds to other main group elements reduces the amount of steric protection available, thereby necessitating bulky and efficient protecting groups[27] to stabilise these compounds, or electron-donating groups to stabilise the electropositive silicon centre[28].
As a result, theoretical methods lend themselves to the study of simple silaaromatic compounds, which are inaccessible by traditional laboratory methods due to facile dimerisation [29]. However, prior work on Si-substituted silabenzenes has been limited to small basis sets (3-21G/STO-2G)[30], and no in-depth analysis of molecular orbital shape exists to date.
To extend this body of work, this mini-project aims to model Si-substituted silabenzenes at a higher level of theory, as permitted by advances in computer processing power. In particular, an analysis of molecular orbitals should shed light on the dimerisation reaction and suggest ways of tuning the reactivity of silaaromatic compounds so as to improve their stability. To this end, a series of Si-substituted silabenzenes 5-8 will be investigated by computational methods, using a range of electron-donating and electron-withdrawing substituents, in order to rationalise the ordering of stability.
Structure Optimisation
Silaaromatic compounds have previously been studied computationally, in investigations of substituent effects[30][31][32] and aromatic systems with multiple Si atoms[33]. In a review of computational methods[33], B3LYP/cc-pVTZ method was found to best replicate the results obtained from high-level CCSD(T)/cc-pVTZ calculations, in comparison to Hartree-Fock, MP2 and CCSD methods; additionally, the B3LYP method has the advantage of faster computational speed than CCSD(T). With this in mind, the silaaromatic structures were first optimised quickly by B3LYP/6-31G(d,p), followed by an optimisation with B3LYP/cc-pVTZ using tight convergence criteria (opt=tight int=ultrafine scf=conver=9).
| Compound | Method | E(RB3LYP) / a.u. | rSi-C(2) / Å | rSi-R / Å | rSi-C(4) / Å | rC(2)-C(5) / Å | ∠C(2)-Si-C(6) / ° |
|---|---|---|---|---|---|---|---|
| Silabenzene 5 | B3LYP/6-31G(d,p) |
-483.60454002 | 1.77 | 1.48 | 3.05 | 3.03 | 109.7 |
| B3LYP/cc-pVTZ | -483.69575115 | 1.77 | 1.47 | 3.04 | 3.02 | 109.7 | |
| 1-Silatoluene 6 | B3LYP/6-31G(d,p) |
-522.93613278 | 1.77 | 1.88 | 3.07 | 3.02 | 108.9 |
| B3LYP/cc-pVTZ | -523.04029957 | 1.77 | 1.87 | 3.05 | 3.02 | 109.0 | |
| 1-phenylsilabenzene 7 | B3LYP/6-31G(d,p) |
-714.67406626 | 1.77 | 1.86 | 3.06 | 3.03 | 109.2 |
| B3LYP/cc-pVTZ | -714.83743197 | 1.77 | 1.85 | 3.05 | 3.02 | 109.2 | |
| 1-methoxysilabenzene 8 | B3LYP/6-31G(d,p) |
-598.17100019 | 1.76 | 1.64 | 3.03 | 3.04 | 111.6 |
| B3LYP/cc-pVTZ | -598.31007496 | 1.76 | 1.63 | 3.02 | 3.03 | 111.6 | |
| 1-tbt-silabenzene[27] | Experimental[34] | 1.77 |
The aromatic Si-C bonds are approximately the same length in all the model compounds. The Si-R bond lengths are comparable for 1-silatoluene 6 and 1-phenylsilabenzene 7 as both are Si-C bonds - this bond is shortened in 7, as is expected from conjugation of the phenyl group to the Si atom and the silabenzene ring.
The aromatic internal C(2)-Si-C(6) bond angles are smaller than the ideal 120°, as in benzene, a phenomenon that might be explained by the tendency of silicon to involve its d orbitals, which have an ideal bond angle of 90°. Consequently, this would favour a bond angle contraction to increase σ-overlap with the orthogonal d orbital lobes. Furthermore, compounds 5-7 have similar bond angles, whereas 8 has a much larger angle of 111.6°. This difference may be explained by the double-bond character of the Si-O bond, which would favour a bond angle of 120°. Under valence-bond theory, one could invoke the argument that the greater double-bond character increases the sp2 hybrid character at Si, favouring the 120° bond angle in 8. Otherwise, another rationalisation could be that the stabilisation brought by the electron density donated from O reduces the need for bonding through d orbitals in 8, therefore giving a larger bond angle.
The Si-C(4) bond distances are interesting because they are related to the isomeric Dewar form of silaaromatic compounds. Experimentally, Dewar-5 may be formed photochemically upon irradiation of 5, while Tokitoh's 1-tbt-silabenzene[27], which is electronically similar to 1-phenylsilabenzene 7[34], isomerised into a silabenzvalene[35]. Comparing the 1,4-distances in silaaromatic systems, silabenzene 5 and 1-methoxysilabenzene 8 have the shortest Si-C(4) distances. Simplistically, it is plausible that species 8, with particularly its short Si-C(4) distances might isomerise to the Dewar form easily.
Frequency Analysis
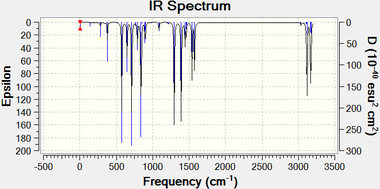
The frequency calculations performed indicate that the structures obtained are sufficiently optimal, with all low frequencies under ±10 cm-1, and only exceeding 10% of the lowest normal frequency in the case of 1-silatoluene 6 and 1-phenylsilabenzene 7.
|
|
| Silabenzene 5 | 1-silatoluene 6 |

|

|
| 1-phenylsilabenzene 7 | 1-methoxysilabenzene 8 |
| Compound | Method | Component | Low frequencies | Lowest frequency | Si-ring deform. | Asym. C-H oop bend | Sym. C-H oop bend | Asym. 2,3 C=C stretch | Sym. 2,3 C=C stretch | Si-R stretch | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Silabenzene 5 | B3LYP/cc-pVTZ SPECTRa | Frequency / cm-1 | -4 | -1 | 0 | 0 | 0 | 8 | 278 | 426 | 585 | 718 | 1295 | 1389 | 2282 |
| Intensity | 3 | 11 | 41 | 60 | 48 | 33 | 72 | ||||||||
| 1-silatoluene 6 | B3LYP/cc-pVTZ SPECTRa | Frequency / cm-1 | -3 | 0 | 0 | 0 | 3 | 6 | 8 | 378 | 575 | 712 | 1296 | 1391 | 1296 |
| Intensity | 0 | 9 | 40 | 51 | 51 | 56 | 5 | ||||||||
| 1-phenylsilabenzene 7 | B3LYP/cc-pVTZ SPECTRa | Frequency / cm-1 | -6 | -3 | -2 | 0 | 0 | 0 | 19 | 249 | 574 | 718 | 1293 | 1391 | 1132 |
| Intensity | 0 | 0 | 37 | 87 | 25 | 64 | 28 | ||||||||
| 1-methoxysilabenzene 8 | B3LYP/cc-pVTZ SPECTRa | Frequency / cm-1 | -5 | 0 | 0 | 0 | 3 | 6 | 59 | 381 | 556 | 714 | 1296 | 1382 | 1128 |
| Intensity | 0 | 4 | 46 | 63 | 86 | 102 | 377 | ||||||||
|

|
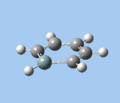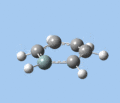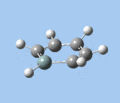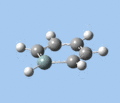
|
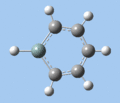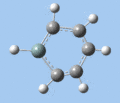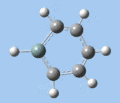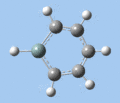
|
|
|
| Ring deformation | Asymmetric C-H out-of-plane bend | Symmetric C-H out-of-plane bend | Asymmetric C=C stretch | Symmetric C=C stretch | Si-R stretch |
Ring deformation
The key ring-deformation mode involves an elongation of the Si-C(4) distance, without any change in the Si-R distance - the substituent undergoes a translation. As the substituent is essentially fixed to the Si atom, the Si-R group may be roughly treated as a single point mass, and the bond deformation modelled after the harmonic oscillator. Consequently, as the frequency of vibrational is inversely proportional to mass, the ring deformation frequency decreases in order of substituent mass 5 > 8 ~ 6 > 7 as predicted by the DFT calculations. The only complication comes in the case of 1-methoxysilabenzene 8, where ring deformation is coupled to bending of the Si-O-Me angle, causing its deformation frequency to be roughly equal to that for 1-silatoluene 6.
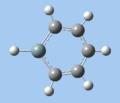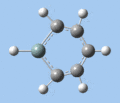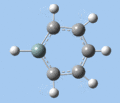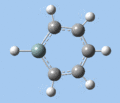
C-H bend, C=C stretch
In all compounds 5-8, the out-of-plane C-H bend and aromatic C=C stretching absorptions are similar in terms of frequency and intensity.
Si-R stretch
The Si-R stretching frequency differs significantly between compounds 5-8 as this is dependent on the Si-R bond. Silabenzene 5 has the highest frequency mode due to the small mass of the hydrogen atom, while the frequencies for compounds 6-8 are in the the typical range for Si-O single bonds. The frequency difference between 1-silatoluene 6 and 1-phenylsilabenzene 7 can be attributed to the difference in substituent mass. In the case of 1-methoxysilabenzene 8, the vibrational frequency is upshifted from the 1000-1100 cm-1 of typical Si-O single bonds, providing further evidence for double-bond character in the Si-O bond.
Effects on Charge Distribution
As electron donation to the electropositive silicon atom is known to stabilise silenes[28], it should be possible to utilise the same effect with silabenzenes. The substituents studied possess a range of electron-withdrawing capabilities, from the mildly electron-withdrawing (H) to more strongly electron-withdrawing groups (Ph).
| Compound | Si(1) | C(2) | C(3) | C(4) |
|---|---|---|---|---|
| Silabenzene 5 | +1.189 | -0.749 | -0.166 | -0.246 |
| 1-silatoluene 6 | +1.480 | -0.780 | -0.162 | -0.259 |
| 1-phenylsilabenzene 7 | +1.497 | -0.774 | -0.160 | -0.258 |
| 1-methoxysilabenzene 8 | +1.775 | -0.824 | -0.150 | -0.284 |
Compounds 6 and 7 have a greater positive charge on Si, as compared to silabenzene 5, due to the higher electronegativity of carbon. This would suggest that silabenzene 5 is more stable than either 6 or 7; however, the lack of any steric protection at Si likely accounts for its instability.
It was thought at first that the methoxy group in 8 would be a strongly electron-donating group by nature of conjugation, as evinced by the Si-O double-bond character. However, the natural population analysis shows that this is completely counteracted by the inductive effect of electronegative oxygen. Nevertheless, the methoxy group increases the electron density at the ortho and para positions by resonance.
|
|
|
|
| Silabenzene 5 | 1-silatoluene 6 | 1-phenylsilabenzene 7 | 1-methoxysilabenzene 8 |
Molecular Orbitals
Silabenzene
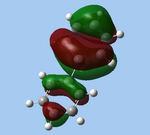
MOs 21, 24, 25, 26 and 27 are analogous to the π MOs in benzene, but are distorted due to the asymmetry introduced by the electropositive silicon atom.
The ordering in energies for MOs 24-27 are interesting because 24/25 and 26/27 are isoenergetic in benzene. In the case of silabenzene 5, the occupied MO 24 with a nodal plane at Si and C4 is lower in energy than MO 25; however the same is not true for MO 27, also with a nodal plane at Si and C4, which is higher in energy than MO 26. This inversion in relative energies can be rationalised by the fact that in both pairs of MOs, there is a differentiation in bonding interactions as a result of symmetry considerations: with MOs 24 and 26, πC-C bonding interactions exist between C2-C3 and C5-C6, whereas with MOs 25 and 27, these have been replaced by relatively weaker πSi-C interactions (MO 25), or else nodal planes exist between all pairs of atoms (MO 27).
MO 15 resembles the structure of Dewar-silabenzene most closely, and would be expected to be involved in any isomerisation to the Dewar isomer.
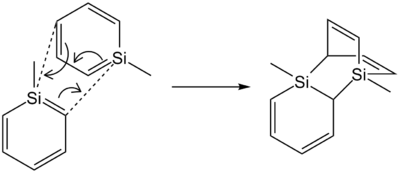
Dimerisation
The dimerisation of simple silabenzenes occurs through a Diels-Alder-type pericyclic mechanism, involving the interaction between the HOMO of the diene (-Si=C-C=C- system) and the LUMO on a separate dienophile molecule (Si=C double bond). A frontier molecular orbital approach shows that the HOMO and LUMO are of the right phase to interact, meaning that dimerisation is thermal rather than photochemical. As such, the orbital and energy overlap between the HOMO and LUMO is crucial to reactivity by dimerisation.
1-phenylsilabenzene 7 has the lowest HOMO-LUMO gap due to stabilisation of the LUMO via conjugation with the phenyl group. This implies a better frontier MO interaction during the dimerisation reaction; therefore, by electronic effects alone, dimerisation of 7 would be expected to be most facile. However, steric considerations might alter the order of reactivity - the steric bulk of the phenyl group might retard the reaction as compared to the completely unhindered silabenzene 5. For instance, Tokitoh's 1-tbt-silabenzene[27] is similar in electronic structure[34] to 1-phenylsilabenzene 7, but does not dimerise under ambient conditions due to steric protection by the bulky tbt group.
Therefore, an accurate ordering of reactivities can only be accomplished by modelling the transition state energies, taking into account not only electronics but also steric effects.
Conclusion
In summary, it was found that a methoxy substituent on silicon does not increase electron density on silicon, against expectations, and therefore would not serve any stabilising function. Additionally, while a molecular orbital analysis of the substituted silabenzenes was useful in reinforcing the frontier molecular orbital understanding of silabenzene dimerisation. While this exercise highlights the utility of natural population analysis and molecular orbital visualisations in understanding the electronics of a reaction, it is evident that considering electronic effects in isolation is insufficient for predicting reactivity. For this, modelling of transition states is necessary to account for the full range of stereoelectronic effects, leading onto the next module of the laboratory course.
References
- ↑ W. Kohn, and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138, DOI:10.1103/PhysRev.140.A1133
- ↑ A.D. Becke, J. Chem. Phys., 1993, 98, 1372–1377, DOI:10.1063/1.464304 .
- ↑ A. D. Becke, J. Chem. Phys., 1993, 98, 5648-5652, DOI:10.1063/1.464913
- ↑ A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100, DOI:[1]
- ↑ S. H. Vosko, L. Wilk, and M. Nusair, Can. J. Phys., 1980, 58, 1200-1211, DOI:10.1139/p80-159 .
- ↑ C. Lee, W. Yang, and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789, DOI:10.1103/PhysRevB.37.785
- ↑ C. E. Check, T. O. Faust, J. M. Bailey, B. J. Wright, T. M. Gilbert, and L. S. Sunderlin, J. Phys. Chem. A, 2001, 105, 8111–8116, DOI:10.1021/jp011945l
- ↑ Y. Yang, M. N. Weaver and K. M. Merz, J. Phys. Chem. A, 2009, 113, 9843–9851, DOI:10.1021/jp807643p
- ↑ 9.0 9.1 9.2 P. Schwerdtfeger, and J. Ischtwan, J. Comp. Chem., 1993, 14, 913-921, DOI:10.1002/jcc.540140806 .
- ↑ J. Glaser, Acta Chem. Scand., 1979, 33A, 789-794, DOI:10.3891/acta.chem.scand.33a-0789 .
- ↑ J. E. D. Davies, and D. A. Long, J. Chem. Soc. A, 1968, 2050-2054, DOI:10.1039/J19680002050 .
- ↑ D. A. Dixon and M.Gutowski, J. Phys. Chem. A, 2005, 109, 5129-5135, DOI:10.1021/jp0445627 .
- ↑ K. Kawaguchi, J. Chem. Phys., 1992, 96, 3411-3415, DOI:10.1063/1.461942 .
- ↑ Experimental spectrum was consistent with D3h geometry.
- ↑ 15.0 15.1 15.2 15.3 D. J. Darensbourg, and R. L. Kump, Inorg. Chem., 1978, 17, 2680-2682, DOI:10.1021/ic50187a062 .
- ↑ P. Hunt, Isomers of Mo(CO)4L2, <http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/10b_MoC4L2_opt.html>, 2011 (accessed 28 November 2011).
- ↑ J. I. Musher, Angew. Chem. Int. Ed., 1969, 8, 54-68, DOI:10.1002/anie.196900541 .
- ↑ D. J. Darensbourg, Inorg. Chem., 1979, 18, 14-17.
- ↑ G. Ferguson, P. J. Roberts, E. C. Alyea, and M. Khan, Inorg. Chem., 1978, 17, 2965–2967, DOI:10.1021/ic50188a058 .
- ↑ W. Hewertson, and H. R. Watson, J. Chem. Soc., 1962, 1490–1494, DOI:10.1039/JR9620001490 .
- ↑ G. Hogarth, and T. Norman, Inorg. Chim. Acta, 1997, 254, 167-171, DOI:10.1016/S0020-1693(96)05133-X
- ↑ 22.0 22.1 F. A. Cotton, D. J. Darensbourg, S. Klein, and B. W. S. Kolthammer, Inorg. Chem., 1982, 21, 294-299, DOI:10.1021/ic00131a055
- ↑ CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC, Boca Raton (YSA), 89th edn, 2008.
- ↑ C. A. Tolman, Chem. Rev., 1977, 77, 313–348, DOI:10.1021/cr60307a002 .
- ↑ T. J. Barton, and G. T. Burns, J. Am. Chem. Soc., 1978, 100, 5246, DOI:10.1021/ja00484a075 .
- ↑ C. L. Kreil, O. L. Chapman, G. T. Burns, and T. J. Barton, J. Am. Chem. Soc., 1980, 102, 841-842, DOI:10.1021/ja00522a068 .
- ↑ 27.0 27.1 27.2 27.3 N. Tokitoh, K. Wakita, R. Okazaki, S. Nagase, P. v. R. Schleyer, and H. Jiao, J. Am. Chem. Soc., 1997, 119, 6951-6952, DOI:10.1021/ja9710924
- ↑ 28.0 28.1 H. Ottosson, and P. G. Steel, Chem. Eur. J., 2006, 12, 1576-1585, DOI:10.1002/chem.200500429 .
- ↑ T. J. Barton, and M. Vuper, J. Am. Chem. Soc., 1981, 103, 6788–6789, DOI:10.1021/ja00412a061
- ↑ 30.0 30.1 K. K. Baldridge, and M. S. Gordon, Organometallics, 1988, 7, 144-155, DOI:10.1021/om00091a023
- ↑ D. M. Dhevi, U. D. Priyakumar, and G. N. Sastry, J. Mol. Struct.-Theochem., 2002, 618, 173-179, DOI:10.1016/S0166-1280(02)00470-0 .
- ↑ A. M. El-Nahas, M. Johansson, and H. Ottosson, Organometallics, 2003, 22, 5556-5566, DOI:10.1021/om030417o .
- ↑ 33.0 33.1 K. K. Baldridge, O. Uzan, and L. M. L. Martin, Organometallics, 2000, 19, 1477-1487, DOI:10.1021/om9903745
- ↑ 34.0 34.1 34.2 N. Tokitoh, K. Wakita, T. Matsumoto, T. Sasamori, R. Okazaki, N. Takagi, M. Kimura, and S. Nagase, J. Chin. Chem. Soc., 2008, 55, 487-507.
- ↑ K. Wakita, N. Tokitoh, R. Okazaki, N. Takagi, and S. Nagase, J. Am. Chem. Soc., 2000, 122, 5648-5649, DOI:10.1021/ja000309i .