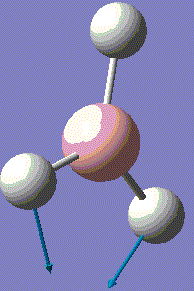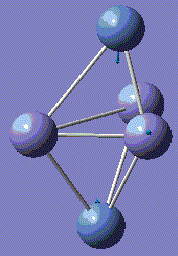Rep:Mod2:yz908

Computational Laboratory-Inorganic

Introduction

Computational chemistry is widely used nowadays in order to give us the knowledge of structure and bonding of complicated molecules. Organic molecules have very defined and clear bonding structures, which are easy to analyse and understand. However, this is not quite the case for inorganic complexes, the relative molecular systems are quite large in space to differentiate. Generally speaking, computational methods and calculations are useful tools for conformational studies on energies of various conformers. This is due to the relative difficulties in analysing transition states and activated complexes, which are extremely hard to characterise experimentally. By using computational chemistry, the relative thermodynamic data can be gained by calculating the optimised structure. Therefore, the kinetics of the reaction and transition state energies could be obtained.

From the previous Organic Computational Analysis, we can see that by optimisation, a series of useful information containing bending and dipole/dipole energies can be obtained. Building upon other methods, IR spectroscopy, NMR calcualtions coudl all be used for characterisation in order to work on the elctronic interaction and orbital interactions of the computer model. All those have been very successful in determing the structure and predicting the correct products. A recent discovery has shown a computational catalyst, which are cheap and extremely efficient in calculations.

To study an inorganic reaction, laboratory experiments are effective in finding out what is actually happending. Besides, computational methods play a important role in understanding the transition states as well. This models can lead to a deep insight into reaction studies at the molecular level. The aim of this computational analysis is to use basis sets in Guassian 3 to obtain the optimised total energies, molecular orbitals, IR frequencies electronic interactions. In the experiment, analysis has been done for BH₃, TlBr₃ and also cis and trans isomers of Mo(CO)₄(PCl₃)₂. This study show a clear success in computational methods and the correct characterisation carried out by calculation. It was then being followed by an mini project to discover the stereoisomeric effect in the Grignard reagent reaction.

Computational Methods

The Ab initio method (based on bonding) is applied in this experiment. This method analyzes the electronic interactions, and is built upon quantum mechanics to derive efficient calculations for the process. Density functional methods are also applied here, including B3LYP, MPW1PW91 to further assist the Ab initio calculations. One of the main benefits of using these tools is that electron density effect and orbital interactions are taken into account for the analysis of geometries and energies.

The calculation was done by Gaussview 3 and 5. Depending on the molecular models used, Density function method or a basis set is applied, which includes different approximation to the Schrodinger Equation. 3-21G and 6-21G models are commonly appled. 3-21G is a basis set with the smallest number of basis function for each calculation. However, the 6-31G set adds larger number of functions to proceed the calculation to a heavier atom. The more the functions used in the process, the slower the reaction and the more expensive the total computational experiment costs.

In this case, Density function method is the main means being undertaken. 3-21G, 6-31, LanL2DZ and LanL2MB are widely applied. Hence, the associated error is determined using other analysis.

Procedure

First of all, the calculation methods are compared and summarised below:

STO-3G: This is built upon Slater Type Orbitals, which were created by mixing three functions into the calculation process. 3-21G: The basis set used in the Schrodinger Equation is described by 3 Gaussian functions to obtain the inner orbitals. Out of the 3 functions, 2 are used to combine the 1st Slater Type Orbitals of the double zeta, 1 is used for the 2nd Slater Type Prbitals of the double zeta. 6-31G: The basis set is described by 6 Gaussian functions to obtain the inner shell orbitals. Out of the 6 functions, 3 are used to combine the 1st Slater Type Orbitals of the double zeta, 1 is used for the 2nd Slater Type Prbitals of the double zeta.

From the comparison, it is easily seen that STO-3G is the simplest basis set, 6-31G is a slightly more detaied basis set.

It is clear that the degree of precision and accuracy are based on the basis set. Therefore the more Gaussian function the basis set involves, the more accurate the calculation will become. This is the reason why after the error discussion, other basis sets are analysed for more accurate results.

Generally speaking, there is an error of 10 kJ/mol(0.003809 Hartree) However, after error discussion for various basis set, it is seen that 3-21G includes only 1% error compared to the results obtained from 6-31G. In conclusion, the total energy calculated should be confirmed to be up to 1 decimal place.

Bond length is recorded close to 0.01 Å. In the experiment, 3-21G method is generally applied and the bond length to 2 decimal places. Bond angle is recorded close to 0.1°. Due to the basis set used, the bond angles are to 0.1°. Frequencies is recorded with no decimal places, however error is known as around 10%. Therefore, the bigger the frequency, the more the error, and the less accurate the results are. Intensity is recorded close to the nearest whole number. Dipole moment is recorded close to 2 decimal places. based on the basis set used, the dipole moment is accurate when to 2 decimal places.

BH₃ Molecular Analysis

In this experiment, a molecule of BH3 was created in Gaussian 3, the instructions in the lab mannual was followed carefully. For calculation and analysis, some knowledge of quantum chemistry was used to look at structures and bonding. This was all done by optimising the molecule of BH3.

Two steps of optimisation: • By assuming the relative positions of Boron and hyfrogen nulei, the Schrodinger equation is solved based on electron cloud and the total energy minimum. • The position of the relative nuclei is calculated, which takes generally longer. After that, the geometry with lowest energy is used. The results are obtained by changing the positions of nuclei untill lowest energy is seen.

The method used here is B3LYP with basis set of 3-21G. In optimisation, OPT was applied. Although 3-21G has low accuracy, the calculation is relatively fast to run.

Background Theory of BH₃

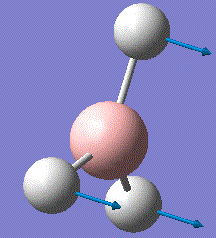
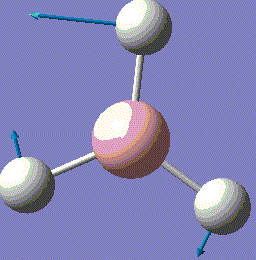
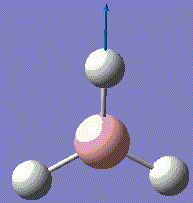
BH3 is very reactive with SP2 hybridised orbitals and a empty horizontal p-orbital, which is electron deficient. BH3 bond with other 3 hydrogen atoms leaving this p-orbital non bonding. Normally, BH3 exists in dimer form. For this computational optimisation, it is assumed that BH3 is in the monomer BH3 form, and no dimerisation will occur during the whole experimental process. The optimized structure is analysed for its vibration frequency, relative atomic positions and MOs near the HOMO-LUMO region. After investigation, an optimised MO diagram would be drawn.

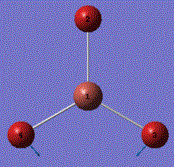
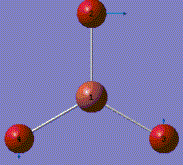
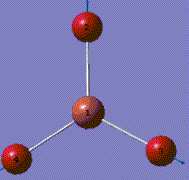
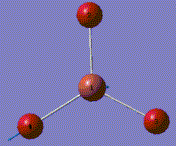
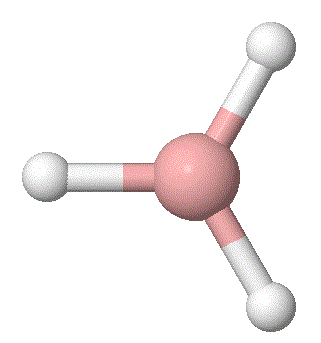
A molecule of BH₃ was generated and optimized using Gaussview. The optimized structure along with the obtained results are shown below (B-H bond length was set to be 1.50 Å):

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy / a.u.	-26.4619
RMS Gradient Norm / a.u.	0.00020669
Dipole Moment / Debye	0.00
Point Group	D3h
Job Time / s	16.0
Final B-H Bond Length / Å	1.19
Final B-H Bond Angle / o	120.0

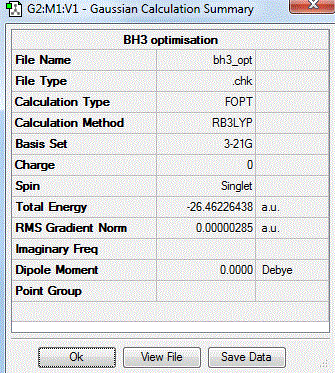
From GaussView 5 optimisation, the new generated file was saved as a log file. The method can be seen as RB3LYP and 3-21G basis set, the calculation type is FOPT. Final energy was calculated as -26.46a.u and dipole moment 0.00D. Using this method, the point group of this BH3 molecule can also be identified as D_3h, molecular geometry is found to be trigonal planar.

By using the inquiry button, optimised B-H bond distance and the optimisd H-B-H bond angle can be measured as 1.19Å, 120 degrees. Literature value found by Allen et al. is 1.19 Å. Literature bond angle in BH3 is also recorded as 120^o. . These computational results have shown a very good agreement with the literature values. Therefore, due to the small size of the molecule, computational calculations does not show a big variation from the actual experimental results.

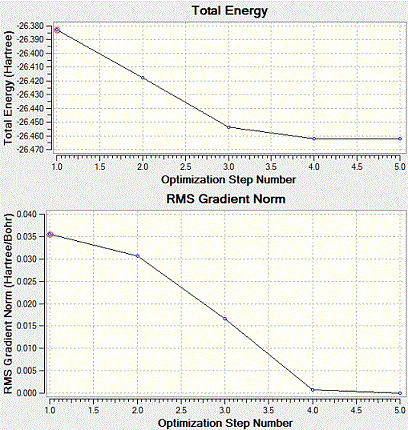
The optimization results are shown above graphically.

The graph of total energy vs step number shows the energy value at different stages of the optimisation process. The root mean square of calculations are taken and the gradient could be obtained from it. The RMS Gradient Norm graph appraoches zero when the optimisation step number increases and total energy reaches the minimum. This observation happens around Step 4 and ends at Step 5. In the energy graph, the gradient is the change between the energy compared to the optimisation steps. Therefore, it could be seen as the frequency of changing optimisation geometry. After the job has been run, the geometry is the most stable and optimised. It is a structure that will be found in the gas-phase. This structure can also be discovered in its solid state (by X-ray crystal structure). However, to avoid distorting the molecule, there should be no solid state forces, crystal packing forces included.

From the graph, it is also seen that when you increase the optimization step number, the total energy of BH3 molecule decreases. That's why when the optimisation proceeds further, a better conformation and geometry is produced.

The way to determine whether the molecule has been optimised is by looking at the force, RMS displacement and maximum displacement values from the output file. All these results must fall under the critical value of 0.00042, 0.0012 and 0.0012. Most importantly, the RMS values must be zero. The output file has therefore been compared and it was shown that the optimization has reached the end by matching the relative measurements.

Output file obtained for BH3 was shown here: Output log file

Molecule Orbital Analysis of BH₃

According to the Molecular Orbital structures, the electronic interations are analysed. 8 molecular orbitals are generated by Gaussian and included in the image above. The relative energies of the molecular orbitals of BH3 and the ones generated by linear combination of molecular orbitals method are summarized and included also in the image. From Comparison, it is identified that the energies of MOs from computational methods match the ones generated by LCAO in terms of shape and energy. In general, the two methods generate orbitals with similar energies, and the computatrional ones show greater mixing. Therefore, the Molecular Orbital theory is very useful in determining the relative orbital energies, predictions are proved by the computational methods.

The energy diagram can also clearly show that the interaction between s orbitals is strong than that between s and p orbitals. That's the reason why the energy of 3a1’ antibonding molecular orbital is generally higher than that of the 2e’ antibonding MOs, and by around 3.9kJ mol^-1 difference. Due to orbital mis-match, and the difference in shape, the overlap between 2 s-orbitals is much better than the overlap between s and p orbitals.

Qualitative Molecular Orbital theory is fairly accurate and precise in terms of obtaining results compared to the computational method. Although the shape of relative molecular orbitals can be obtained easily, the relative energies of those orbitals are quite difficult to obtain. The computational method is accurate in finding the energies, but failed to predict the order in which the orbitals are filled. This is because of the absence of electron cloud in the antibonding orbitals. This problem could possibly be improved by introducing a more precise basis set, ie 6-311G, which has more functions in calculations to gain the results.

Natural Bond Orbital Analysis of BH₃

The basis sets 3-21G and B3LYP methods are used in this natural bond orbital analysis. By looking at the localised electron distribution. The atomic charges can be determined, and used as to identify the lewis acid and lewis base properties of the moleculs. Results are discussed below:

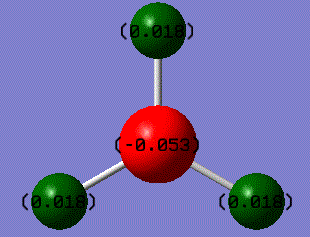
The boron atom at the centre of the BH₃ molecule is sp² hybridized. As found before, the dipole moment of this BH3 molecule is defined to be as zero. This is therefore in a good agreement with the results shown on the image above. This is because the sum of the '+ve' charges (green) of all the hydrogen atoms is the same as the '-ve' charge (red) on the boron atom numerically. By looking at the symmetry and geometry of this molecule, BH₃ has a rotational axis though the boron atom.

Boron is electron deficient due to the empty p orbital perpendicular to the plane of the molecule. This is the reason why boron shows a '-ve' charge (electronegative) at the centre of the molecule, and hydrogen atoms show '+ve' charges(electropositive) on the sides. BH₃ is therefore a strong Lewis acid.

Natural Bond Orbital analysis indicates that the three hydrogen atoms are of fully s-orbital character, however the boron atom are identified as with 1/3 s-character and 2/3 p-character. These results are found to be consistent with the prediction by computational methods.

Vibrational Frequency Analysis of BH₃

The vibration frequencies of the BH₃ molecule is analysed and recorded. Results and vibrational modes are computed below. It is identified that all those vibration frequencies recorded are having a positive number, which is a indication of fully completion of the optimisation job. The point group of BH₃ is found to be D_3H according to previous findings, and the methods used are still 3-21G and B3LYP.

The log file of the vibration frequency analysis for BH₃ molecule is here: Output log file

Order	Figure of motion	Type of Vibration	Text	Frequency /cm-1	Literature valueFrequency /cm-1	Intensity	Assigned Point Group
1		Out-of-Plane Wagging	The H-atoms move in and out of the molecular plane of BH3 in the same direction at the same time, however, borom atom is moving in the other direction compared to hydrogens with a relatively lighter amplitude	1146.03	1147	92.6653	A2
2		In-plane Scissoring	Two H-atoms in the BH3 molecule move in and out from each other with the boron centre and the other hydrogen atom remain unchanged or move relatively perpendicular to the BH3 plane at a lighter amplitude	1204.86	1201	12.3919	E'
3		In-plane Rocking	The BH3 exerts a in-plane rocking motion with two hydrogen atoms anf the boron centre moving constantly and the other hydrogen atom rocks in the other direction at a relatively heavier magnitude.	1204.86	1201	12.3944	E'
4		Symmetric Stretch	All hydrogen atoms move away from of towards the boron centre in the BH3 molecular plane at the same time. It is indicated that the boron centre remains stationary.	2591.65	2501	0	A1'
5		Asymmetric Stretch	One of the hydrogen atoms in BH3 keeps stationary and the boron centre and 2 other hydrogen atoms move away from or towards the centre at a slightly smaller amplitude.	2730.07	2602	103.8565	E'
6		Asymmetric Stretch	Two hydrogen atoms move towards and away to and from the boron centre in a symmetric fashion in the BH3 plane. The other hydrogen atom moves in and out of the plane in the opposite direction.	2730.07	2602	103.8497	E'

The BH₃ molecule is not linear, therfore it has 3N-6 vibration modes and N indicates the number of atoms in the molecule. For BH3, there are 4 atoms, and 3*4-6=6, so in total 6 vibrational motions are found. From the table above, is it seen that out of the six vibrations, 3 of which are translational vibrations and 3 other ones are rotational vibrations.

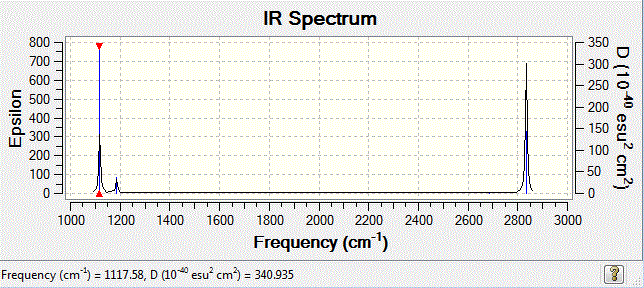
The IR spectrum can also be considered with only 3 major frequencies are seen. Although this results is not normal, the observation is found to be consistent with the vibrational modes above. This is due to the two pairs of degenerate modes of 2 vibration frequencies at 1204cm^-1 and 2730cm^-1 respectively. It is also observed that one of the vibration has a intensity of zero, which is due to the symmetric stretching of boron-hydrogen bond. Therefore, the dipole moment opposes each other and disappears. This is because in IR spectroscopy, the intensity corresponds to the relative dipole dipole moment during vibrations. When the stretches are symmetric, low intensity is seen due to low small dipole moment.

Generally speaking, as the vibrational frequency rises, the results obtained from computational methods start to shift from the optimum. The explanation for this variation can be attributed to the anharmonic motion of the vibrations, therefore the results contain certain level of inaccuracy. To achieve the best results, concerted motion and harmonic vibrations must be maintained.. In conclusion, the computational results are in a good agreement with the real IR spetrum when at relatively lower frequencies.

TlBr₃ Molecular Analysis

Background Theory of TlBr₃

In this experiment, the geometry of TlBr3 molecule is optimised using GaussView 5. TlBr3 has a trigonal planar structure similar to BH₃. It is therefore suggested that the dipole moment and bond stretching frequencies are of the same magnitude and similar values. The symmetry point group of TlBr₃ is also found to be D_3h.

Optimisation of TlBr₃

The molecule of TlBr₃ is analysed and optimized using GaussView 5. Due to the large size of the Tl atom compared to the boron atom, the method used by last experiment for BH3 is not applicable any more. Therefore, the minimal basis set is changed from 3-21G to LanL2DZ with other parameters kept the same.

File Type	.log
Calculation Type	FOPT
Basis Set	LANL2MB
Final Energy / a.u.	-69.4392 a.u.
RMS Gradient Norm / a.u.	0.00005901
Dipole Moment / Debye	0.00
Point Group	D3h
Job Time / s	13.0
B-H Bond Length / Å	2.64
B-H Bond Angle / o	120.0

For viewing the 3D structure:

From the summary shown above, the optimisation gives a TlBr₃ conformation consistent with the model built from Baeck et al. In the literature, the bond angle is found to be 120.0^o, geometry is trigonal planar, and the point group also to be D_3h. From the optimisation values, it is clearly shown that the total energy of the optimal geometry is around -91.11 a.u. with bond length to be 2.64Å. Glaser et al has reported that the literature value for Tl-bromium bond length is 2.51Å with bond angle 120_o It is identified that with the use of LanL2DZ basis set, bond angle is correctly identified but not so true for the bond length.

Output file obtained for TlBr3 was shown here: Output log file

Vibrational Frequency Analysis of TlBr₃

After running Gaussview 5.0 for optimization. The bonds between Tl and Br atoms are not appearing in the window. This is due to display issues associated with the method. The programme can only show specific bonds which are within the bond length range of certain values. Sometimes, the bonds are too long to be processed, therefore it will not show up in the display window. Since GaussView structures are mainly based on organic molecules, the inorganic molecules often have these difficulties of viewing clear bonds.

Chemical bonds are existing between two or more atoms. There are metallic, covalent and ionic bonds. Ionic bonds are electrostatic attraction between positive ions and negative ions. Metallic bonds are electrostatic attractions between positive metal cations and delocalised electrons. Covalent bonds are simple formed between two atoms and electrons are shared between both two.

To analyze TlBr₃, basis set LanL2DZ was used. Different vibrational frequencies are summarized below:

Order	pictures	Vibration names	Text	Frequency /cm-1	Intensity	Point Group
1		In-plane Scissoring	The in plane bromine atoms are moving in the different direction as the Tl atom, the other bromine atom is moving in the different direction.	45	4	E'
2		In-plane Rocking	The Tl atom and 2 bromine atoms experience a in plane rocking motion, the other bromine atom wags along the molecular plane and moe with a slightly larger amplitude.	45	4	E'
3		Out-out-plane Wagging	The bromine atom moves in and out of the plane at the same time, the Tl atom is vibrating in the opposite direction with a slightly smaller amplitude.	53	6	A2'
4		Symmetric Stretch	All of the three bromine atoms in the molecule move symmetrically in and out of the plane from the Tl centre. The Tl atom at the centre of molecule keeps stationary.	164	0	A1'
5		Asymmetric Stretch	One bromine atom keeps stationary with the Tl atom only wags in a slow motion. All the other 3 bromine atoms move in and out of the Tl centre.	211	25	E'
6		Asymmetric Stretch	Two bromine atoms move inwards or outwards from the Tl centre at the same time. However, the other bromine atom moves towards or away from the Tl centre in the opposite direction.	211	25	E'

With the help of the motion table above, it is seen that there are two pairs of degenerate vibration motions showing at 45cm^-1 and 211cm^-1. Of those 6 different vibrations, one of which has no peaks in the infrared spectroscopy. Therefore, only 3 frequency peaks are seen in the infrared spectrum (apart from the motion, which has zero intensity) . Because of the similarity of vibration motions of In-plane Scissoring and In-plane Twisting, also between asymmetric stretches, frequencies are the same. Therefore, peaks match each other in position and go on top of each other. Broader peaks are seen and there is no dipole moment for the whole molecule.

To ensure the final energy is an optimum, the frequencies are seen as positive values. From comparison, it has been believed that the vibration values for TlBr₃ are relatively smaller than that for BH₃ generally. This is because of the lightness of the BH₃ molecule. Therefore, for the same energy input, BH₃ molecule will be stimulated more and vibrated via more motions and larger amplitude. That's the reason why for TlBr₃, the vibration frequencies are relatively lower.

GaussView Problems

As described, the bonds between atoms might not show up in some circumstances when using GaussView 5. Those bonds do exist, however, due to the programme limitations, sometimes are not viewed. Normally for organic structures, the bonds are much shorted than the inorganic ones.

Another question was raised on the bond length. Before the optimisation of the molecule BH₃, bond length was set to be fixed at 1.5Å. After running the calculations, it was recored as 1.18Å. This is another reason for the bonds to vanish in the later case.

Mo(CO)₄L₂ Molecular Analysis

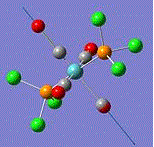
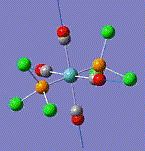
In this experiment, the Density Function Theory is applied to obtain the cis and tran isomers of Mo(CO)₄(PCl3)₂.TThe basis set LANL2DZ was used here for better and more accurate calculations, this is mainly due to the relatively large molecular size. The spectroscopic properties are analysed here with infrared spectrum and other technique.

By optimisation of the molecular structure, electronic density and the bonding characteristics are investigated. when the ligand is used to be L=PPh3, the spectrum will have four CO absorption bands if there are cis ligands, and only one CO band when there are trans ligands. The thermal stabilities are analysed, in which the trans isomer is more stable according to thermodynamics. Due to the point group difference, the isomeric properties are effected by the relative IR bands. In the spectra, CO bands are strongly focused. Speaking of point groups, the cis isomer has a C2v point group and the trans D4h. Therefore, the cis isomer brings about 4 CO peaks and trans with only 1 CO peaks. The intensity of IR peaks are defined by the dipole moments, in which the bigger the dipole moment, the strong the IR bands.

Optimisation of Mo(CO)₄Cl₂

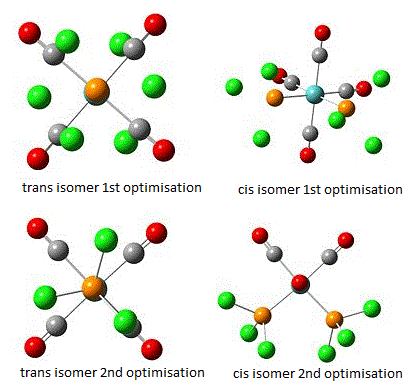
Both the cis and trans isomers of Mo(CO)₄(PCl₃)₂ best structures are calculated in Gaussian. LanL2MB basis set was used to achieve the best optimisation. The process was then repeated again to obtain the second optimisation, including bond rotation to gain the most stable conformation.

The calculation results are shown below, indicating the first optimisation on the top and the second optimisation at the bottom:

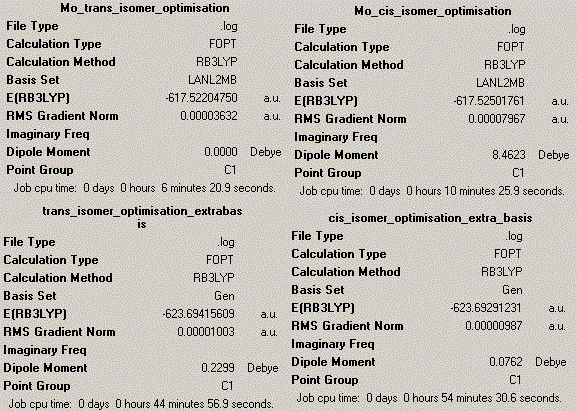
Basis set RB3LYP and LANL2MB were both applied in this calculation and analysis. LANL2MB is particularly chosen over the basis set 3-21G due to a much heavier element used in this example. Molybdenum is quite large atom compared to some other atoms. Using these methods, the optimum total energy and dipole moments and bond lengths are identified for Mo-P and P-Cl. Due to a lack of references and literature results, the Mo experiment is therefore compared with the Cr results, this is possible because of the presence of same period in the periodic table for Cr and Mo.

Features	trans-(calc)	Lit values of trans-	Cis-(calc)	Lit values of tran-
Dipole moment /D	0.00	None	8.32	N/A
Total Energy /a.u	-617.13	N/A	-617.23	N/A
RMS Gradient	0.000040	N/A	0.00020	N.A
Mo-P Bond Length /Å	2.47	2.37	2.51	2.48
Mo-C Bond Length /Å	2.10	1.87	2.06	2.03
P-Mo-P Bond Angle /o	180.0	175.9	95.4	103.5
P-Mo-C(trans) Bond Angle /o	88.4	89.3	175.5	162.9
P-Mo-C(Cis) Bond Angle /o	N/A	N.A	90.5	80.1

Cis-isomer has a dipole moment of 8.32D whereas the trans- isomer has only zero, which is due to the fact that the trans isomer is symmetrical and any other interaction will get cancelled out. Steric hindrince affects the results as well. With bulky groups, it increases significantly. With trans- isomers, the 2 bulky groups are quite far away from each other, so the effect is not significantly large. As a general trend, trans- isomer should be more stable than the cis- isomer. However, here this is not the case due to the fact that the cis isomer is around 8 kJmol^-1 more stable than the trans isomer.

According to the trans theoty, carbonyl groups are strong trans-directing ligands. Because of the fact that there are less CO groups found in the cis isomer, the molecule is less susceptible to trans effect and more stable.

From comparison with the literature values, it is seen that the computational results are similar to the theoretical results. However, upon second optimisation, the conformation is being made much more stable, due to a better structural arrangement. The second optimisation was done by the LANL2DZ basis set with results shown below:

Features	trans-(calc)	Lit values of trans-	cis-(calc)	Lit values of trans-
Dipole moment /D	0.30	N/A	1.32	N/A
Total Energy /a.u	-623.536	N/A	-623.565	N/A
RMS gradient	0.0000025	N/A	0.00000550	N/A
Mo-P Bond Length /Å	2.39	2.32	2.54	2.59
Mo-C Bond Length /Å	2.07	1.86	2.03	2.07
P-Mo-P Bond Angle /o	177.2	176.4	94.1	104.4
P-Mo-C(trans) Bond Angle /o	89.5	89.9	174.6	163.9
P-Mo-C(cis) Bond Angle /o	N/A	N.A	89.1	80.6

After second optimisation, the energies are found to be even smaller, which means structures more stable. RMS tells the fact that the optimisation process has completed. The second results are generally more reliable and accurate. Generally speaking, the cis- isomer is more stable than the trans isomer.

IR and Frequency Analysis of isomers

Four major vibrational frequencies are summarized below:

Isomer	Form of Vibration	Frequency / cm-1	Intensity	Symmetry (C1 Point Group)
trans-Mo(CO)4(PCl3)2	Twisting of CO ligands: The Mo atom and the CO groups move at the same time, while chlorine atoms moves in the opposite direction. Phosphorus keeps stationary	4	0	A
trans-Mo(CO)4(PCl3)2	:Twisting of PCl3 ligand: The chlorine atoms on one of the PCl3 ligands move in the different direction to the chlorine atoms on the other PCl3 ligand; trans CO groups move in opposite direction as each other with small amplitude as well. Mo, P keeps stationary	6	0	A
cis-Mo(CO)4(PCl3)2	: Twisting around the P-Mo-P axis: The Mo atom and the CO groups move at the same time, while the PCl3 ligands move in the opposite direction ad Mo(CO)4	11	0	A
cis-Mo(CO)4(PCl3)2	: Twisting of the PCl3 ligand: The CO groups move together, while the PCl3 ligands move in the opposite directions; Mo keeps stationary.	18	0	A

From the table above, it is clearly shown that most vibrations are rocking and twisting based. At room temperature pressure, there are only slight and weak vibrations associated. This is due to the bond stretching is very energy demanding.

The CO group stretches are IR active, so the frequencies are analysed and discussed below:

Isomers	Frequency /cm-1	Intensity	Lit Frequencies /cm-1	Point Group
Trans-	1948	1463	1887	Eu
Trans-	1949	1459	1899	Eu
Trans-	1947	1	None	B1G
Trans	2023	4	None	A1G
Cis-	1943	763	1986	B2
Cis-	1947	1487	1985	B1
Cis-	1949	628	2002	A1
Cis-	2921	589	2093	A1

From the table above, it is seen that 2 of the 4 CO stretches are of particularly low intensity. This is too weak to be visible on the IR spectrum. At the same time, some stretches superimpose, so the peak number decreases. For the trans- isomer, there is only one band shown in the spectrum. The degenerate peaks are coming from the asymmetric stretch of CO group. Therefore, that's why only 1 peak is seen in the spectrum. Another reason might be due to the weak dipole dipole moment that the intensity is low. ALl the results shown are in a good agreement with the literature values found at 1899 cm^-1 . Metal carbonyl compounds are generally believed to have only one IR band in the spectrum if it has a trans geometry. Therefore, when there are four IR bands, it will have a cis conformation. According to the conputational evidence, this point has been proved and the geometry of molecules could be predicted.

Mini Project-Si₄ and Fe₃Ni₂

The aim of this mini project is to study the physical and chemical properties of small metallic cluster. Recalling from the theory, the structure of metal clusters changes significantly when adding and taking electrons away from the relative positions. Numerous scientific researches have been done in inorganic clusters regarding the significant properties and applications. In this mini project, minimum total energies, bond lengths and bond angles are studies in order to analyse the structure from different aspects regarding NBO and vibrational frequencies.

Introduction

There are a lot recent research activities in the reactivity of nine-atom deltahedral clusters of group 14, which are known as deltahedral Zintl ions. The redox chemistry of these species and their ability to form oligomers, polymers, and functionalized clusters are commonly seen. The cluster geometries, bonding and electronic structures are widely analysed.

The studies of isomers of Si4 and Ni4 metal clusters are extremely popular. According to the literature, there are functional calculations being performed on cluster models with point charges to further understand the surface properties. Si4 is a non-planar square. Ni4 occupies tetrahedral arrangement very close to gas-phase structure. Si4 bonds are generally stronger than Ni4 ones. Bonding in metallic clusters is quite different. Generally speaking is a mixture of 2c-2e and 3c-2c bonds. The electrons could be imagined by covering the whole structure with delocalised electron cloud. The structure could be calculated by Wade's Rule. .

Si₄ optimisation

Si₄ has been studies by Kuznetsov et al to identify the two possible isomers with point group D_2h, C_2v and T_d. A series of silicon clusters exist in various charge states (Si₄2+, Si₄, Si₄2-, and NaSi4). They are generally being studied by photoelectron spectroscopy. Bonding in this structures could be well illustrated using aromaticity with addition or removal of two electrons.

First, the total energies for the three point group structures are optimised as follows and the log file for the optimisation of Si₄ molecule is here: Output log file

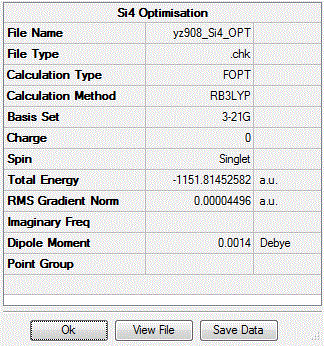
Point group of Si4	Td	D4h	C2v
Energy /a.u	-15.28	-15.28	-15.32
Dipole Moment	0.002	0.0001	0.0002
Bond Length

Two possible structures for Si4 are the tetrahedral Td and square-planar D4h arrangements proposed by Slee et al . According to computational results, it is identified that the C_2v is a much more stable structure after optimization. The total energy of C_2v is therefore lower compared to the other two proposed structures. Si₄ cluster takes up a C_2v arrangment because of the relative sizes of the Si atoms. Si has an atomic radius of around 1.5Å, therefore, the cluster is relatively stable in C_2v.

IR and Frequency Analysis of Si₄

When optimisation is completed, the structure was taken for further analysis. It is proved to have the lowest energy. The vibrational frequencies for Si₄ in C_2v are measured using Gaussian and obtained in the table below. According to the results, the almost zero frequencies are a sign of showing the minimum total energy has been obtained. Further characterisation using IR spectroscopy has also been carried out.

Looking at the table, there are three different vibrations considered to be IR visible due to the asymmetric motion in and out of the plane. Vibration 1 and 2 could be seen as degenerate because of the fact that they are moving in a rocking fashion and they both have nearly zero intensity. The low intensity as mentioned earlier is due to the small change in dipole moments. As Vibration 4-6 has larger dipole moment, it therefore will appear as higher intensity in the IR spectrum. All the prediction and actual computational results are consistent with the theory in literature. The computational method is considered to be very sufficient in predicting chemical properties for isomeric structures.

The vibrational frequencis and IR spectrum for Si4 are shown below and the log file of the vibration frequency analysis for Si₄ molecule is here: Output log file

Order	vibration images	Frequency /cm-1	Intensity	Point Group
1		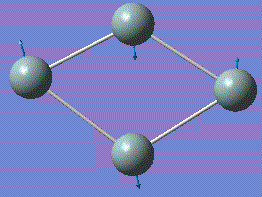116.74	0.9262	A
2		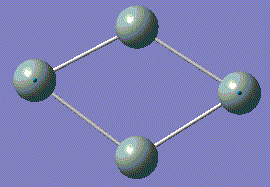119.02	0.3365	A
3		265.73	0.7103	A
4		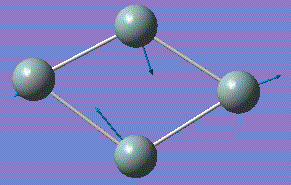294.29	3.1831	A
5		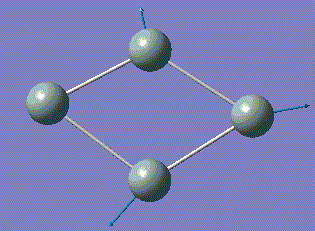351.61	20.1151	A
6		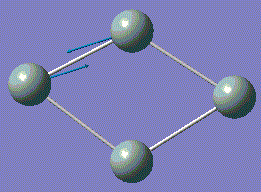408.59	51.6055	A

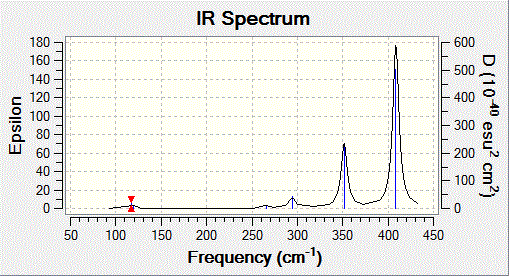
According to the vibration analysis, all the frequencies are shown to be obove zero, which means that the optimised conformation has the minimum total energy. Si4 has four silicon atoms, and using the 3N-6 equation when N equals 4, there are 6 vibrations for this non-linear cluster. The vibrational frequencies of Si₄ are generally quite high due to stronger bonding system in the cluster structure. This is the reason why silicon atoms are normally vibrating at slightly higher frequencies.

Natural Bond Orbital Analysis of Si₄

The NBO analysis is applied to determine the overall charges over the Si₄ cluster structure. This has been done by using Gaussian charge function and the results and distribution are shown below:

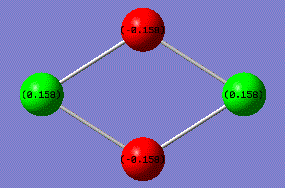
According to the results calculated earlier, the overall charge was determined to be 0.0002. However, the previous discussion has confirmed the dipole moment of this Si₄ cluster to be overall zero. By focusing on the geometry and charge of the molecule, Si atoms at left and right side of the structure have positive charges(green +0.158), and the vertical two silicon atoms therefore has negative charge (red -0.158).

Charges cancel each other out giving an overall zero. Computational result in consistent with the theory.

Molecular Orbital Analysis of Si₄

Molecular Orbital Analysis can efficiently lead to the determination of chemical properties and reactivity. Normally, the chemistry is controlled by the electron cloud around the HOMO-LUMO region. The MOs below are generated by using Gaussian programme and the HOMO-LUMO levels are studied.

The structure of neutral molecule Si₄ is obtained by adding two electrons, Si₄ is seen to be either p-antiaromatic or sr-antiaromatic,depending on the MO level the 2 electrons enter. The sr-antiaromatic system is rhombic, and the p-antiaromatic system is expected to be rectangular. The rhombus structure was found to be the optimised structure with a lowest total energy. The rhombus structure, produced by Raghavachari et al is well known to be the global minimum for Si₄, and the sr-antiaromaticity of Si₄ providesthe natural explanation for the rhombic distortion. However, the Si₄ rhombus can still be viewed as p-aromatic and st-aromatic due to the presence of the two fully bonding p and st MOs.

Table 13. The MO of Si₄ cluster.

MO Type	MO image	MO energy/a.u	MO Symmetry
HOMO -1		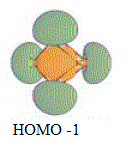-0.237	Pσ-r
HOMO		-0.229	Pσ-t
LUMO		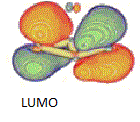-0.146	Pπ
LUMO +1		-0.107	Pπ
LUMO +2		-0.096	Pσ-t

The structure and bonding could be illustrated using the theory of aromaticity and antiaromaticity. The Si isomers were produced experimentally and characterized by photoelectron spectroscopy. By adding two pairs of electrons, Si₄is p-aromatic and s-antiaromatic. Chemical bonding of tetramers of Si could then be understood. The molecular orbitals are then generated by pp, ps-r, and ps-t atomic orbitals of specific element. It is clearly identified three MOs: pp-based, ps-r-based and ps-t-based. Of all those molecular orbitals, the bonding ones are always the one with lowest energy, and the antibonding ones the highest energy. The middle molecular orbitals are generally degenarate. The newly introdeced MO sets are: p aromaticity from pp MOs, and s aromaticity from the ps-r and ps-t MOs.

There are 8 electrons in the Si₄ cluster in total. Based on 4N+2 Huckle aromaticity, Si₄ is antiaromatic due to the 2 extra delocalised electrons.

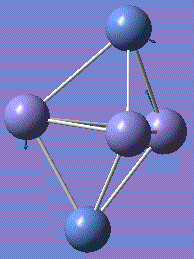
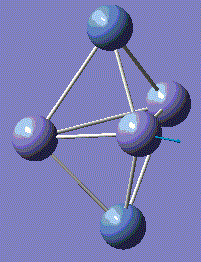
Fe₃Ni₂ optimisation

Metal clusters are constructed by metal-metal bonds. Here, the Fe-Ni clusters are studied. Generally speaking, Fe and Ni atoms show a range of clusters including Fe₁Ni₄, Fe₂Ni₃, Fe₃Ni₂, etc. These Fe-Ni clusters can be used in catalysis, and biological reactions.

Metal-Metal bonds are nomally d-interactions. Due to the large size of the atoms, the bond lengths are quite large. Therefore, values are normally discovered between the bond length or Fe-Fe and Ni-Ni lengths.

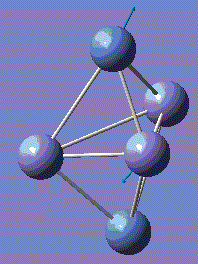
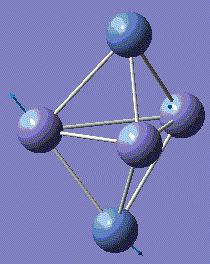
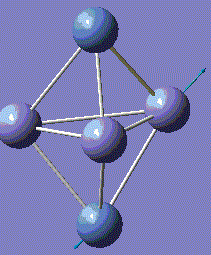
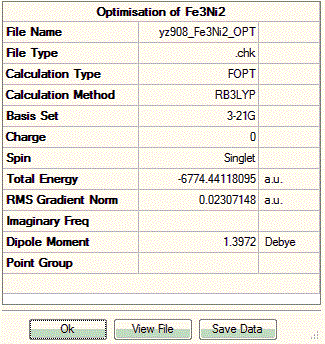
With computational methods using GaussView 5, the structure of Fe₃Ni₂ is optimised as follows and the log file of the vibration frequency analysis for Fe₃Ni₂ molecule is here: Output log file

After obtaining the summary and results, the charge distribution is shown as below:

This Fe-Ni metal cluster has an overall charge of zero, which is consistent with the theoretical value.

The vibrational frequencis and IR spectrum for Si4 are shown below and the log file of the vibration frequency analysis for Fe₃Ni₂ molecule is here: Output log file

Order	vibration images	Frequency /cm-1	Intensity	Point Group
1		-215.04	7.6668
2		-110.01	4.4552
3		12.68	2.5510
4		79.92	0.6478
5		106.12	0.0678
6		136.11	2.5298
7		160.95	2.6976
8		179.92	1.8755
9		285	7.1866

Conclusion: The total energies, optimised geometries of pure Fe-Ni clusters have been obtained using computational Gaussian Methods. Upon investigation, the cluster structure exhibit some degree of distortion, which will increase as the number of Fe atoms increases in the Fe-Ni cluster. Regarding to these 5-atom clusters, and by investigation into similar structures of Fe-Ni clusters, the lowest total energy ones appear when Fe–Fe bonds is maximal and the Ni–Ni bonds remains minimal. By optimisation, it is determined that the energetic ground state of Fe–Ni clusters is defined from the maximization of Fe–Fe and Fe–Ni bonds.

Conclusion

Computational method are useful technique for molecular optimisation, which gives reasonable energy minimum and geometry bestsuit. It then becomes available to calculate and discover further information about the optimised structures, such as bond length, bond angle and total energy.. Characterisation methods are also used to analyse the IR and NMR also vibrational frequencies to predict reactivity. Molecular Orbital Theory is also a efficient tool in discovering the electron activity and HOMO-LUMO electron interactions. Therefore, in inorganic computational analysis, the properties of ligand chemistry and reactivity could be measured and analysed. Experiments done above have clearly demonstrated all the points, and computational methods have been successful in use by applying basis sets either B3LYP or 6-311G depending on molecular size.