Rep:Mod2:xy307
Module Introduction
Computational inorganic chemistry provides information about the structure and bonding of complexes. Comparing to organic molecules, the situation is not straight forward in many cases due to the complicated valence shell structure and bonding ability in inorganic chemistry. Computational chemistry could help us pick up the relative stable isomers or conformers from hundreds of possibility by calculating the relative energy. Based on the optimized structure, it also enables us to study properties such as dipole moments, molecular orbitals, IR spectra and NMR spectra. These information is extremely useful for some compounds which are hard to purify or unstable under detection conditions. With the help of computational chemistry, scientists could determine the direction of researches easier without repeatedly tests numerous amalogues.
The content of this module focuses on some basic idears of computational inorganic chemistry, comprising analysis of BH3, BCl3, Cis-/Trans- isomers of Mo(CO)4Cl2, and a mini project about the structure and properties of tetrasulphur tetranitride, S4N4.
General Note on Accuracy and Convention
- Total energies are reported in atomic unit of Hartree (E'h').
- Relative energies are reported in kJ/mol, and are only valid for systems under the same type of calculation with identical number and type of atoms.
- The energy calculate has an error of ≈ 10 kJ/mol, which is equivalent of 0.00381 Hartree(1Eh = 2625.5 kJ/mol)
- The dipole moment is accurate to about 2 decimal places, i.e., 0.01 Debye.
- Frequencies in wavenumbers are by convention reported to the nearest whole integer with stematic error of around 10%, the error may be relatively very large for high energy vibrations, e.g., 300cm-1 for C-H stretch at 3000cm-1
- Intensities are reported to the nearest integers by convention although accuracy is much less than this.
- Bond distances are accurate to ≈ 0.01 Å
- Bond angles are accurate to ≈ 0.1°
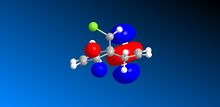
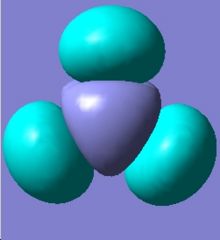
Analysis of a molecule of BH3
Optimizing the Geometry
A BH3 molecule was drew in GuassView 3.09 and the B-H bond lengths were defined manually to be 1.5 Å. The geometry optimisation was carried out on personal computer using Gaussian. The method used is DFT-B3LYP, and 3-21G was chosen as the basis set
since the molecule is small and the calcuation criteria is simple, involving DFT (Density Function Theory) B3LYP method, and 3-21G basis set:
# opt b3lyp/3-21g geom=connectivity BH3 Optimisation 0 1
- Output log: XUEZHENG_BH3_OPT.log
- Calculation summary: BH3_opt_summary.jpg
The optimised geometry showss the B-H bond length is 1.19(4435)Å and the H-B-H bond angle is 120.0°. To confirm that the calculation has indeed converged, the information below "Item" in the log file has been checked. In the optimisation all the forces and displacements criteria are converged, and the optimisation was properly executed in Gaussian.
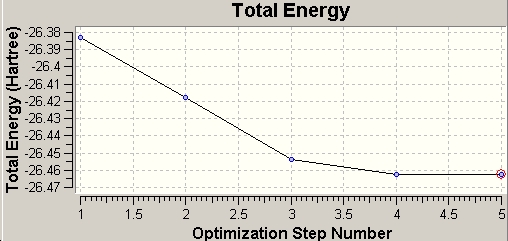
During the optimisation, Gaussian recorded both total energy change and root mean square gradient change, which can be shown in GaussView.
 |
 |
The total energy diagram shows that the Gaussian optimises the PES of BH3 and finally reaches the minimum energy geometry at -26.46a.u.. At this point, the RMS gradient also decreases to its minimum, ~0, which means within a specific limit the energy won't change. In other words, the molecule reaches the most stable conformation.
Analysis of the Molecular Orbitals (MO)and Natural Bond Orbitals (NBO)
Molecular Orbitals of BH3
Using the .chk (checkpoint) file from the gemometry optimisation, a new Gaussian input file was generated by adding the keywords "pop=full,nbo" for the NBO analysis of BH3. Below is the details of calculation:
# b3lyp/3-21g pop=(nbo,full) geom=connectivity BH<sub>3</sub> MO analysis 0 1
- Output log: XUEZHENG_BH3_POP.LOG
- Results summary: MO_summary.jpg
The MOs can be visualised via the .chk file from the calculation and the lowest energy MOs of BH3 are calculated from HOMO-3 to LUMO+3. The graphs are grabbed and pasted below (Fig. 3.1-3.8):
 |
 |
 |
 |
 |
 |
 |
 |
The MO calculations are in good agreement with theoretica prodictions by LCAO approach. Tge comparison between LCAO prediction and Gaussian calculations are illustrated below. From the diagram we could see they are almost the same.
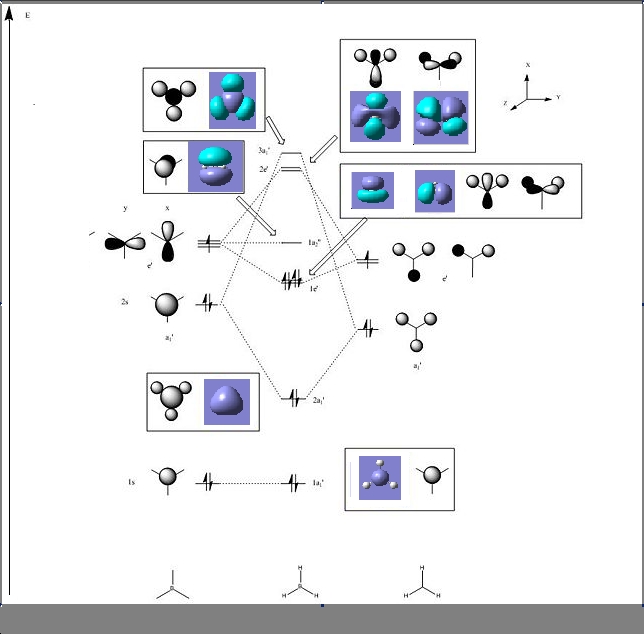
Comparing to the LCAO predictions, the Gaussian calculation at DFT-B3LYP, 3-21G level not only provides generally MO shapes, but also tells some details about the blending and shapes, especially at the interfere regions of the orbitals in space. For HOMO-3, HOMO-2 and LUMO, LUMO+3, both sets of orbitals gave good descriptions of the MOs. However, for HOMO, the Gaussian calculation is superior because the LCAO didn't approximate how the blending or orbitals would affect the size of the MO.For LUMO+1 and LUMO+2, it is apparent that the computed MOs provided more details than LCAO, regarding both the blending across the molcule and also the resulting repulsions that arise from the MOs.
Natural Bond Orbital Analysis of BH3
GaussView could show charge distribution from the NBO output file. The distribution can be visualised with colour according to the positive/negative of each atom of BH3. The numerical values can be also displayed on these atoms. It could be seen the charges are 0.331 for B and -0.110 for H.
The NBO analysis gives much more powerful information rather than just charge distribution. It also gives the contribution from each atom to different bonds. The more detailed information must be read directly from the .log file: a selection of the log file is here: (Nbosummary.txt).
In the "Bond orbital/Coefficients/Hybrids" section which describes the bonding information of the molecule, the log shows in each boron-hydrogen bondm, 55.51% of the elcectron density comes from the H and 44.49% comes from the B. Furthermore, one can see that the B orbitals are hybridised from 33.33% sAO and 66.67% pAO. Thus B has formed 3 sp2 hybridised orbitals which each interact with the sAO of the H atom.
It can also be seen that orbital 4 is the core (CR) 1sAO which is comprised exclusively from B.
To identify the vacant p orbital on B, the LUMO (the lowest energy orbital) is studied. from the "Natural Bond Orbitals (Summary)" section. Orbital 8 is the only unoccupied orbital with negative energy (-0.045), which is unusual. The property of this orbital allows BH3 acts as a Lewis acid and it is easy to accept an electron. Further research into orbital 8 indicates the 2pz AO is unoccupied and 2px and 2py are not fully occupied. In the "Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis" section, where it states the interactions between the different MOs (e.g. mixing), one can see that there is no second order interactions in the case of BH3, as the energies of the E(2) column are too small to cause any significant changes (1.51 kcal/mol. or cf. 20.0 kcal/mol).
Analysis of the Vibrations
The DFT-B3LYP method and 3-21G basis were used to carry out vibration studies. After optimisation by Gaussian, the following information was obtained.
# freq b3lyp/3-21g geom=connectivity pop=(full,nbo) BH3 frequency 0 1
- Output log: XUEZHENG_BH3_FREQ.LOG
- Summary: Bh3freq.jpg
In the log file, the total energy remained the same as the optimised geometry, which means the frequency study is right. The summary shows BH3 belongs to D3h symmetry group. There are 6 vibrations computed from Gaussian, and each one is associated with a symmetry operator.
| Table 1.1.2 - Vibrations of BH3 molecule | |||||
|---|---|---|---|---|---|
| No. | Vibration | Frequency / cm-1 | IR Intensity | Symmetry (D3h) | Description of Vibration |
| 1 |  |
1146 | 93 | A2'' | H atoms move orthogonal to the σh plane concerted, and B displaces a little bit. |
| 2 |  |
1205 | 12 | E' | Concerted scissoring motion of two H in σh plane and small displacement of B |
| 3 |  |
1205 | 12 | E' | Scissoring motion of two hydrogens, and rocking of the other, all in the σh plane. Small B displacement |
| 4 |  |
2593 | 0 | A1' | All three ydrogen atoms concertedy, symmetrically stretch in the σh plane |
| 5 |  |
2731 | 104 | E' | Asymmetric stretch of two hydrogens in σh plane |
| 6 |  |
2731 | 104 | E' | Symmetric stretch of two hydrogens, both antisymmetic with other vibration of the third hydrogen, all in σh plane |
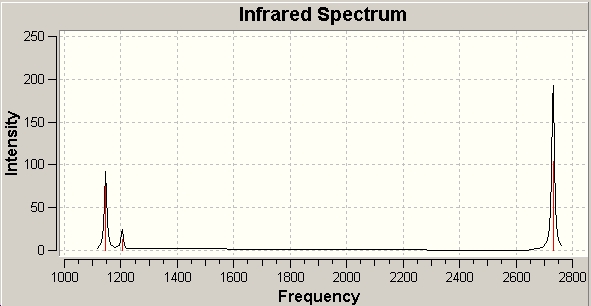
There are 6 vibration in the BH3 molecule from the data above. However, we cannot see 6 peaks in the IR spectrum (Fig. 6). It is because the expected peak at 2593cm-1 is completely centriosymmetric, thus it doesn't change dipole moments of the molecule. (0 IR intensity) Among the other 5 IR active peaks, 2 set of degenerate vibrations appear at 1205 and 2737 cm-1, so the peaks can be seen is 3.
Analysis of a Molecule of BCl3
Geometry Optimization
In GaussView, BCl3 was prepared with the B-Cl bond defined at 1.87Å, and a symmetry of D3h. The pseudo-potential basis set was used this time (DFT-B3YYP/LANL2MB).
# opt b3lyp/lanl2mb geom=connectivity BCl3 optimisation 0 1
- Output log: XUEZHENG_BCL3_OPT.LOG
- Results summary:Bcl3summary.jpg
The molecule still retained a D3h symmetry after optimisation, with the B-Cl bond lengths were all 1.86(592) Å, and all H-B-H bond angles were 120.0°.
Vibration Analysis
The frequency calculation was based on DFT-B3LYP/LanL2MB as instructed, no addtional keywords were used in the calculation.
# freq b3lyp/lanl2mb geom=connectivity BCl3 frequency 0 1
- Output log: XUEZHENG_BCL3_FREQ.LOG
- Results summary: Bcl3freq.jpg
The vibaration of BH3 is similar to BH3 , with 6 peaks (214, 214, 377, 417, 939 and 939 cm-1), which also have the same symmetry element as the corresponding BH3 orbitals. All these frequencies are positive which proves we get a minimum rather than a transition state in the optimisation.
Questions on BCl3
The calculations of both geometry optimisation and frequency use DFT-B3LYP method and LanL2MB basis set as instructed. The set muct be consistent for a series of relavant calcultaions, which make sure the result is valid and comparable.
Basis sets determine the complexity of calculation involved in describing the electronic structure. Larger basis sets usually means better and more detailed results. However, it also need more calculations, which costs time and money. The best basis set for computation is a balance between accuracy and efficiency in each case.
The optimised BCl3 has a B-Cl bond length of 1.86(592)Å, and the H-B-H bond angles are 120.0°. The values are in accordance with literature. [1].
The symmetry group of BCl3 is D3h as expect expected. The ground state of the molecule has a geometry of trigonal planar.
GaussView may do not display the existing bonds somtimes, as the case in BH3 optimisations above. It is due to GaussView set a default length for each specific bond. If the bond length is greater than the default value, the software "thinks" the bond does not exist. During BCl3 calculations, we could find before optimisation, the repulsion was strong and the chlorine atoms are further apart form each other so that the bond length is greater than the software recognition.
A classical definition of bond is that bond can be described as the attractive association between atoms or ions that is stable under the conditions of examination[2]. As the theory develops, bond nowadays can be described as a distribution of electron density between atoms.
Both the optimisation and frequency calculation took only 13 seconds on PC, which is because the structure is simple and highly symmetrical, and the method and basis set used is not complicated as well.
Cis-/trans-isomerism of Mo(CO)4(PCl3)2
Introduction
The vibration spectra of C=O of the cis/trans-isomers of Mo(CO)4L2 (L=PPh3) are quite different. The cis-isomer has 4 different absoptions whereas the trans-isomer only have one band. The difference in IR activity is related to the symmetry of the complex.
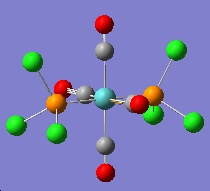
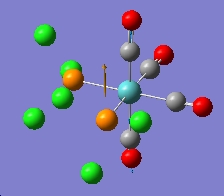
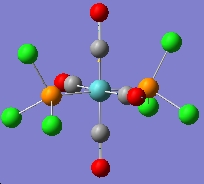
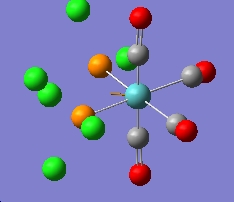
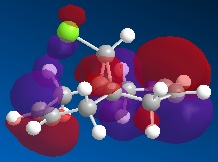
In this section the complex Mo(CO)4(PCl3)2 is investigated. This complex is very similar to the one mentioned above, but the L group is much simpler and easier to be calculated. The structures of them are shown in the figures below. The aim of this part is to find out why these conformers have different IR bands from computational optimisation and prediction.
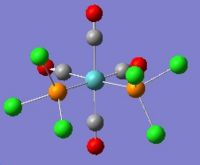
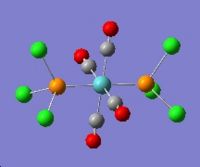
Geometry Optimisation of Mo(CO)4(PCl3)2
Both cis- and trans- Mo(CO)4(PCl3)2 were drawn in GuassView. Then they were optimized by DFT-B3LYP method using LanL2MB basis set. An additional keywords"opt=loose" were added to allow the weak method to converge at a less critically defined minimum.
The results of the first cis-isomer optimisation is publshed on D-space and can be found here,:D-space reference: [1]
Similary the optmisation was conducted on the trans-isomer. The result is deposited on D-space can be seen found here, :D-space reference: [2]
The two PCl3 groups are in a staggered conformation in the cis-isomer, while the two groups on the trans-isomer did not have any particular symmetry.
The .out files of the cis- and trans-isomers were modified in GaussView again to get more accurate results. For the cis-isomer the PCl3 groups were rotated such that one Cl was synperiplanar to one of the co-cis-carbonyls, and one Cl on the other PCl3 group was antiperiplanar to the same carbonyl. This was done by modifying the torsion angles to 0° and 180° respectively.
The trans-isomer structure was also modified to diplay the eclipsed confomration with respect to the PCl3 groups, as well as having a dihedral angle of 0° between on Cl atom on the substitution group and one of the carbonyl groups.
Finally, the modified isomeric structures undergoes a DFT-B3LYP/LanL2DZ geometry optimization with additional keywords "int=ultrafine scf=conver=9", which uses a stronger method and a larger basis set with increasing electronic convergence.
The code for the modified optimisation:
# opt b3lyp/lanl2dz geom=connectivity extrabasis int=ultrafine scf=conver=9 trans/cis optimization 0 1
The log file for the Cis-isomer can be found at :D-space reference: [3]
The log file for the Trans-isomer can be found at :D-space reference: [4]
Frequency Analysis of Mo(CO)4(PCl3)2
In this section, the vibrational frequencies were calculated based on the geometry optimised output (The advantage is that we could check the effectiveness of the optimisation since negative vibration frequencies means incomplete optimisation).
The code for the frequency analysis:
# freq b3lyp/lanl2dz geom=connectivity extrabasis int=ultrafine scf=conver=9 trans/cis frequency 0 1
Log file for cis-isomer is stored at :D-space reference: [5]. Log file for trans-isomer is stored at :D-space reference: [6]
From the log files, it was found that while the cis-frequency analysis converged, the trans-frequency analysis did not converge fully:
Convergence data from the trans-isomer frequency analysis:
| Item | Value | Threshold | Converged? | |
| Maximum | Force | 0.000007 | 0.000450 | YES |
| RMS | Force | 0.000002 | 0.000300 | YES |
| Maximum | Displacement | 0.034199 | 0.001800 | NO |
| RMS | Displacement | 0.008597 | 0.001200 | NO |
Convergence data from the cis- isomer frequency analysis:
| Item | Value | Threshold | Converged? | |
| Maximum | Force | 0.000023 | 0.000450 | YES |
| RMS | Force | 0.000009 | 0.000300 | YES |
| Maximum | Displacement | 0.003586 | 0.001800 | NO |
| RMS | Displacement | 0.001074 | 0.001200 | YES |
The forces are well converged in the trans-isomer, but the displacement is not. It is not significant to cause problems, since the force is more important and it is reasonable below the threshold in the case. As a consequence, furthur optimisation with more complicated methods and basis sets are not necessary.
A possible reason could be that the geometry of the optimised trans-isomer does not own an inversion centre actually, as the P-Mo-P bond angle is 177° in trans-isomer, while it was defined as 180° before optimisation. The distorted geometry leads to the loss of symmetry and during the frequency analysis as the log file did not display any symmetry label. So does the case in cis-isomer, while the default dihedral angle at 0° becomes ~6° after optimisaion.
Results Discussion and Answers to Questions on [Mo(CO)4(PPh3)2]
Geometry Optimisation and Energy
From the Table, the cis- and trans-isomers displayed some tiny differences in total energies. The ciss-isomer has a slightly more negative energy and thus it is the more stable comformer.
| Energies of cis/trans-[Mo(CO)4(PCl3)2] | |||
|---|---|---|---|
| Isomer | Energy / Eh | Energy / kJ mol-1 | Relative Energy / kJ mol-1 |
| Trans | -623.57603112 | -1637198.87 | 0 |
| Cis | -623.57707194 | -1637202.602 | -2.73 |
The css-isomer is more stable, which is NOT in agreement with the reference.[3]. However, the difference is only 2.73kJ/mol. If the substituent alternates to PPh3, the case may change. The steric large groups favous trans position to each other to minimise the repultion. The reason for the unexpected result is that for small groups such as Cl, stereoelectronic effect may dominates the steric effect. Another possible reason is the simplicity of method and basis set can not describe the situation properly.
The cis-isomer belongs to C2v point group, while the trans-one belongs to the D4h point group. The table below is a comparison between trans-isomer and its analogous complex based on chronium.
| Geometric parameters of trans-isomer and its chromonium analogue | ||
|---|---|---|
| Parameter | trans- Cr(CO)4(PPh3)2, lit.[4] | trans- Mo(CO)4(PCl3)2, calc |
| P-M (avg.) / Å | 2.3656(16) | 2.0603(05) |
| M-C (avg.) / Å | 1.8716 | 2.4450 |
| P-M-P / ° | 176.69(6) | 177.39(2) |
| P-M-C (avg.) / ° | 89.54(15) | 90.00(30) |
From the table, it can be seen that the values are in very good agreement. The bond lengths are longer for Mo complex because of its longer covalent radius relative to Cr (1.54 Å vs. 1.39 Å[5]).This is as expected and can be explained since the metals moves to the next period with larger shape.
Cis- Mo(CO)4(PPh3)2 is used as a literature reference for the cis-isomer of Mo(CO)4(PCl3)2:
| Geometric parameters of cis- Mo(CO)4(PCl3)2 | ||
|---|---|---|
| Parameter | cis- Mo(CO)4(PPh3)2, lit | cis- Mo(CO)4(PCl3)2, opt |
| P-Mo (avg.) / Å | 2.577(2) | 2.511(9) |
| Mo-C (avg.) / Å | 2.041(4) | 2.347(3) |
| P-Mo-P / ° | 104.62(7) | 95.16(4) |
| P-Mo-C (trans) / ° | 163.7(2) | 176.0(8) |
| P-Mo-C (cis) / ° | 80.6(2) | 89.2(2) |
The large differences are due to the steric hindance of bulk Ph groups on phosphorous. Comparing to the literature, the optimisation is reasonable.
Vibrations
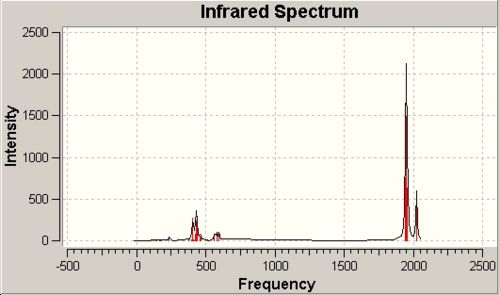
The IR spectra of the cis-/trans- isomers of the Mo(CO)4(PCl3)2 complex are illustrated in Fig.9a and Fig. 9b respectively.
 |
 |
In the previous assumption, it is expected only 3 active peaks in cis-isomer IR and 1 in trans. Surprisingly, the calculation gives all four peaks in the spectra. If we magnify the spectrum, we can even distinguish the peaks very close to each other. The reason is that during assumption we think the molecule is highly symmetric, whereas after optimisation, we can find there will be a little deviation from the ideal conditions. As a result, the theoretical inactive vibration also changes the dipole moment and become active.
The literature[6] values for Mo(CO)4(PPh3)2 matches the calculation very pooly. This is caused by the difference between phenyl and chlorine substituents.
| CO vibrations of trans-isomer | CO vibrations of cis-isomer | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Vibration | Description | Frequency / cm-1 | IR Intensity | Symmetry (D4h) | Vibration | Description | Frequency / cm-1 | IR Intensity | Symmetry (C2v) |
 |
strong antisymmetric A-trans vibration of C=O; weak symmetric vibration of B-trans C=O | 1950 | 1475 | eu |  |
strong antisymmetric vibration of axial C=O; weak asymmetric vibration of equitorial C=O | 1945 | 1765 | b2 |
 |
strong antisymmetric vibration of B-trans C=O | 1951 | 1567 | eu |  |
weak antisymmetric vibration of axial C=O; strong antisymmetric vibration of equitorial C=O | 1948 | 1498 | b1 |
 |
Moderate symmetric vibration of A-trans C=O, antisymmetric to moderate symmetric vibration of B-trans C=O | 1977 | 1 | a1g |  |
moderate symmetric vibration of axial C=O, antisymmetric to strong symmetric vibration of equitorial C=O | 1958 | 632 | a1 |
 |
moderate symmetric vibration of all C=O | 2031 | 4 | a1g |  |
moderate symmetric vibration of all C=O | 2023 | 598 | a1 |
The calculation also shows some low energy vibarations which can not be seen under usual experimental conditions:
| Low energy vibrations of Mo(CO)4(PCl3)2 | ||||
|---|---|---|---|---|
| Isomer | Frequency / cm-1 | IR Intensity | ||
| trans | 5 | 0 | ||
| 6 | 0 | |||
| cis | 11 | 0 | ||
| 18 | 0 | |||
Mini-Project: Tetrasulphur tetranitride - an Interesting Structure
Introduction
The best known sulphur-nitrogen cage is S4N4, which is an orange-yellow crystalline material. The compound is kinetically stable in air but endothermic with respect to its constituent elements and exploded when heated or stuck.
Unlike other endothermic kinetically stable compounds, which are very complicated, S4N4 is extremely simple and can be conveniently synthesised through direct reaction of NH3 and SCl2/S2Cl2, which makes it easily accessible to study the properties of these kinds compounds. It is also an important precursor to prepare a series of sulphur nitride, including the polymer (SN)x, a one dimentional conductor with a conductivity similar to mercury. The diversity in reactivity and physical properties attract many researchers.[7]
One of the most interesting things about tetrasulphur tetranitride is its structure. As known, large aliphatic rings usually to take a staggerd conformation so that each member of the ring can adopt a sp3 arrangement for its bonds and unbonding electron pairs. However, S4N4 has a strange structure with a square plane of N atoms lying within a tetrahedron of S atoms.
In the project, the molecular structure will be investigated using the DFT-B3LYP method and a basis set of 6-31G. Then the MO and NBO will be calculated upon this moedel and the following questions will be addressed
- Why does S4N4 take the special conformation?
- What is the energy difference between these conformers?
- How is the charge distributed over the molecule?
- What is HOMO-LUMO region looks like?
- Do the transannular S-S bonds exist?
Geometry Optimisation
Tetrasulphur tetrnitride can be drawn as several different conformers using ChemDraw 3D. Two typical sutructures were chosen for analysis. One is the Lu and Donohue structure from X-ray diffraction, with transannular pseudo S-S interactions, and the other is a totally staggered one based on the model of large aliphatic rings.
Firstly, both of the comformers were prepared in GaussView and undertook geometry optimisation using DFT-B3LYP method with 6-31G basis set:
# opt b3lyp/6-31g geom=connectivity title card required 0 1
The log file for the staggered conformer can be found at D-space reference: [7] The log file for the Lu-Donohue conformer can be found at D-space reference: [8]
In the staggered structure, there are two slightly different bonds lengths, 1.75 Å and 1.81 Å, and the total energy is -1811.2283a.u.. In the Lu-Donohue model, only one bond length at 1.78Å, and the total energy is -1811.2465a.u.. The energy difference is 0.0182a.u. and the Lu-Donohue model has a lower energy, which means it is more stable. The bond length difference in staggered model indicates the single-double bond structure. Unlike benzene, in which the two bonds can interchange by fast resonance, it is a little difficult for staggered model to change the position of double bonds. In the Lu-Donohue model, the almost equal bond length illustrates the highly symmetry of the structure and there may be spatial delocalisation of electron density.
NBO Charge Distribution
The NBO analysis uses the same optimisation methods, with an additional keywords "pop=full":
# b3lyp/6-31g pop=(nbo,full) geom=connectivity S4N4/S4N4 staggered optimisation 0 1
The output file is deposited on D-space and can be found at[9] and [10]
 |
 |
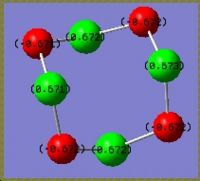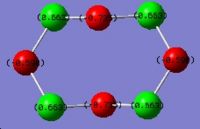The result shows on the actual structure, charges are equally distributed on the same kind of atoms. On S, it is 0.672 and on N it is -0.672. The fact is in good agreement with the bonding information that all the bonds in the molecule is the same. Considering the electronegativity, negative charge on nitrogen is a reasonable result. In the pseudo staggered structure, all the sulphur atoms are still the same with a positive charge of 0.663 whereas the nitrogen atoms are not equivalent any more. Two of them have a charge of -0.590 and the other two are -0.735. A possible explaination is the stereoelectronic effect. The more negative nitrogens get electron density from the antiperiplanar lone pairs on adjacent sulphur atoms. For the less negative ones, the antiperiplanar positions are S-N bonds. These electrons are tightly attracted by both sulphur and nitrogen and not labile for contribution into other orbitals.
Molecular Orbital Analysis of Tetrasulphur tetranitride
The molecular orbitals can be generated and visualised from the output .fch files. The HOMO-LUMO region, which is often of most interest in reactivities and other properties are illustrated below:
 E= -0.053a.u. |
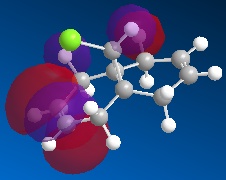 E= -0.093a.u. |
E= -0.172a.u. |
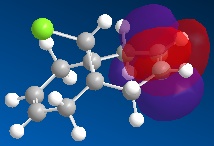 E= -0.172a.u. |
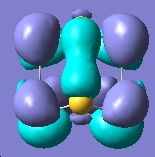 E= -0.266a.u. |
 E= -0.277a.u. |
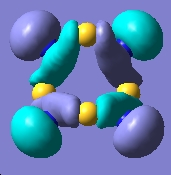 E= -0.310a.u. |
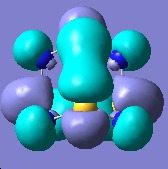 E= -0.314a.u. |
The output log file is deposited on D-space and can be found at: [11]
The MO analysis provides some interesting information about the molecule. Firstly, there are 6 unoccupied MO with negative energy, which means the molecule has a strong ability to accomodate electrons thermodynamically. Thus it may be possible to form a stable anion. The HOMO-LUMO gap is 246.8kJ/mol(0.094a.u.), it is not very large, proving that the kinetical stability at room temperature, but unstable upon heated or struck. The HOMO and HOMO-3 molecular orbitals show interaction between transannular sulphur atoms. It can be regarded as a "bond" interaction in classical bond theory. The "bond length" between the two atoms is 3.08Å, which is less than the sum of the van der Waals radii(3.30Å), but higher than S-S single bond length(2.05Å). The fact corresponds to the weakness the interaction. Experiment data shows the S-S bond length is 2.59Å and 2.71Å separately and the S-N bond length is 1.78Å, which are all less than the predictions. The difference may comes from the simplicity of method and basis set chosen.
Vibration Analysis
Based on the geometry optimisation, the DFT-B3LYP method and 6-31G basis set are used to prediction of vibrations, with the additional words "int=ultrafine scf=conver=9".
The output file of the Lu-Donohue model is deposited on D-space and can be found at: [12]
The output file of the staggered model is deposited on D-space and can be found at: [13]
The predicted vibrational spectra are illustrated below:
 |
 |
Comparing to the literature values[8], the prediction fails to achieve a reasonable result. The reason is the method and basis set used is not sophiscated enough. To solve the problem, more advanced method and basis set should be used. For instance, LanL2MB for optimisation and then LanL2DZ basis set for prediction. However, I've run out of time for more detailed trials. The failure is a proof of the impotance of choosing suitable methods and basis sets in computational chemistry.
References
- ↑ W. Gerrard and M. F. Lappert, Reactions Of Boron richloride With Organic Compounds, Chemical Reviews, 1958, 58,1081–1111
- ↑ Gilbert N. Lewis, The Atom and the Molecule, Journal of the American Chemical Society, 1916, 38, 772
- ↑ A.D. Allen and P.F. Barrett. Phosphine-substituted carbonyl halide complexes of chromium and molybdenum. Canadian Journal of Chemistry,46:1649 1653, '1968'.
- ↑ D. W. Bennett, T. A. Siddiquee, D. T. Haworth, S. E. Kabir, F. K. Camellia, J. Chem. Crys., 2004, 34, 353-359.DOI:10.1023/B:JOCC.0000028667.12964.28
- ↑ B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J.Echeverría, E. Cremades, F. Barragán, S. Alvarez, Dalton Trans., 2008, 2832 - 2838.
- ↑ D. J. Darensbourg, R. L. Kump, Inorg. Chem., 1978, 17, 2680-2682.
- ↑ D. M. Labes, P. Love and L. F. Nichols, Chemical Reviews., 1979, 79, 1-15.DOI:10.1021/cr60317a002
- ↑ D. Chapman and A. G. Massey, Transactions of the Faraday Society., 1962, 58, 1291-1298.DOI:10.1039/TF9625801291