Rep:Mod2:ss6309

Siegfried Stow - Module 2 - Inorganic

1 - BH₃

Optimisation

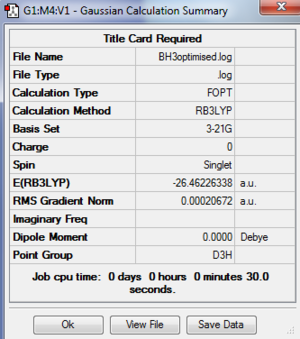
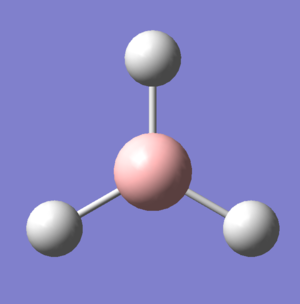
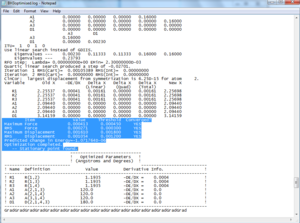
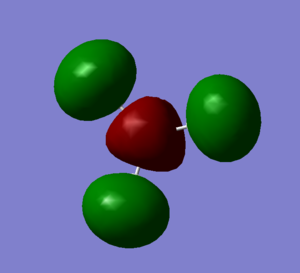
A BH3 molecule was created in Gaussview, the bond lengths changed to 1.5A and then the structure optimised using DFT:B3LYP:3-21G basis sets. the results showed a trigonal planar molecule with bond lengths 1.19A and 120^o. the summary confirmed that the point group was D₃h.

Optimisation Outputs

	image	comment
Summary		D3h point group correctly assigned, the program has identified that the bond lengths are all identical as expected and there is no distortion along the C3 axis. the molecule has no dipole because it is symmetrical.
Starting conformation		the B-H bond length was set to 1.50A, with the hydrogens all on the same plane and with the bond angle at 120o.
Final conformation		the molecule converged with the B-H bond distance 1.19A.
Convergence graph		the molecule converged in 4 steps, the energy decreased quickly up to step 3, where the gradient decreased to 0.005. at the completion of step 4 the program analysed that the gradient was less than 0.001, the convergence threshold, and terminated the optimisation.
Convergence data		the highlighted text is the data from the final optimisation step which shows the thresholds for the four criteria that are used to determine convergence. the 'predicted decrease in energy field' indicates that the energy of the optimisation step has decreased by a tiny amount, in this case converting to ~2.4J/mol (not kJ!), and that further optimisation steps will not decrease the energy significantly. The optimization assumes that the energy approaches the true value asymptotically, which is sensible for small molecules. for some molecules tight-convergence might be required, in order to ensure that the asymptote really is the true conformational energy and not a red herring.

NBO analysis

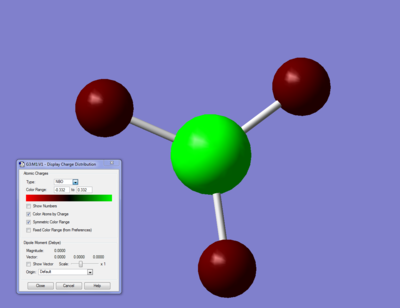
Summary of Natural Population Analysis:                 
                                                        
                                      Natural Population
               Natural  -----------------------------------------------
   Atom  No    Charge         Core      Valence    Rydberg      Total
-----------------------------------------------------------------------
     B    1    0.33161      1.99903     2.66936    0.00000     4.66839
     H    2   -0.11054      0.00000     1.11021    0.00032     1.11054
     H    3   -0.11054      0.00000     1.11021    0.00032     1.11054
     H    4   -0.11054      0.00000     1.11021    0.00032     1.11054
=======================================================================
  * Total *    0.00000      1.99903     6.00000    0.00097     8.00000

Clearly Boron has two electrons which are considered 'core' by the program (1s), and has 2.67 valence electrons, because there are 0.11 extra electrons on each hydrogen. this gives each hydrogen a slight negative charge (-0.11e) and gives the Boron a slight positive charge (0.33). this also makes boron a good lewis acid.

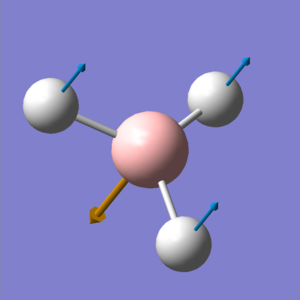
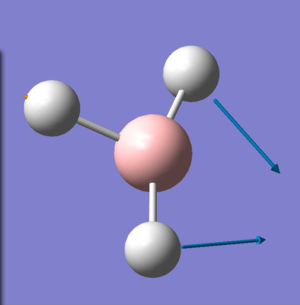
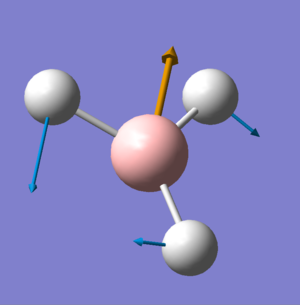
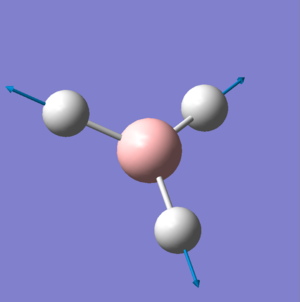
Vibration Analysis

The spectrum clearly shows three vibration absorptions at 1144, 1203 and 2737 cm^-1. analysis of the data shows a more interesting picture.

in reality there two other absorptions that are degenerate, and one which doesn't absorb at all.

Vibrational Analysis

Vibration	Label	Abs	Comment
	C3v	93	this is a symmetric bending of all the B-H bonds together. the absorption is strong because the dipole changes a large amount as indicated by the orange arrow.
	C2v	12.3	a symmetric bending of two hydrogens in plane bending toward each other and then away from each other. the dipole change is quite small so the absorbance is small
	Cs	12.3	the bond angle between two hydrogens stays the same whilst the third wags. again the dipole change is not large so absorbance is predicted to be low. This vibration is degenerate with the previous vibration and is of Cs symmetry. the net movement of the atoms contributes to equal frequency and magnitude of dipole change.
	D3h	00	There is no absorbance for this vibration as there is no change in dipole. all three bond lengths stretch simultaneously so symmetry doesn't change. more advanced spectroscopic techniques would be required to detect this stretch experimentally.
	Cs	103	asymmetric stretch of two hydrogens whilst the third maintains the same bond length. there is a large change in dipole and so the absorbance is very high.
	C2v	103	degenerate with the previous stretch, here two Boron-hydrogen bonds stretch together whilst the third stretches out of phase. whilst not of the same point group the dipole changes equivalently so they are degenerate.

Clearly, the point groups of the molecular vibrations indicate that some of the vibrations will be degenerate, and in the case of vibration 4 because there is no change in symmetry and no change in dipole that it cannot absorb in the infra-red.

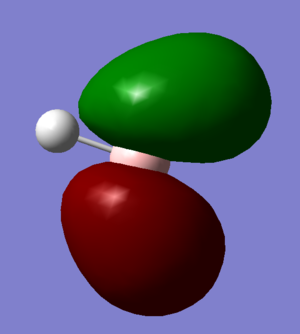
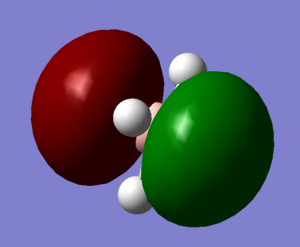
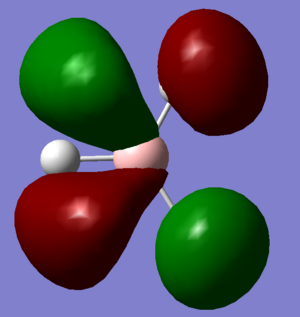
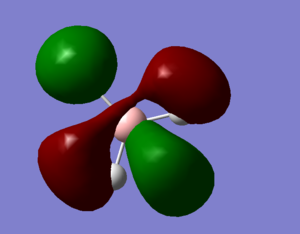
Molecular Orbitals and Diagram

caption

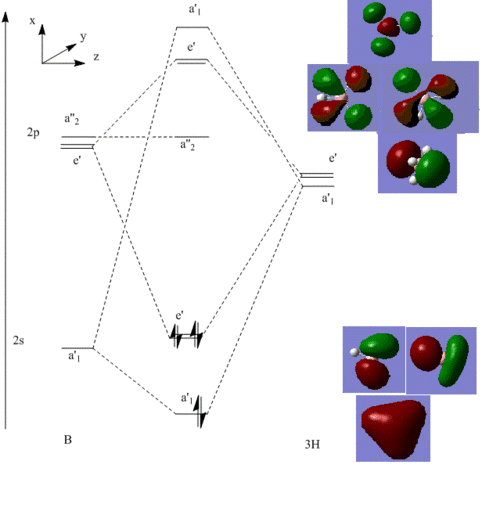The Actual quantitative MOs look very similar to the qualitative LCAOs. The only major exception is that on interaction there is some distortion of the P and S orbitals which is particularly obvious for the antibonding orbitals. in these cases repulsion betwenn opposite phases distorts the p orbital contribution of the MO to be bent away from the repulsive hydrogen 1s AO contributions, which are themselves distorted so that they lie further away, almost to the point of exposing the spheres gaussian draws to represent the nucleus. (the spheres are obviously much larger than the nucleus)

caption

MO	Comment
	fully bonding orbital from the a' B2s orbital and H1s orbitals
	e' orbital from the B 2pz orbital interacting with two hydrogens in phase (green) and one hydrogen of the other phase (red)
	the Boron 2px orbital interacting with one proton of each phase and one orthogonal.
	this is the unoccupied and non-bonding vacant p-orbital. Boron is electron deficient and could readily accept electrons into this site.
	more diffuse anti-bonding orbitals. note that they appear similar to d-type orbitals. this orbital demonstrates distortion of the boron 2p orbital away from the out-of-phase hydrogen 1s orbitals
	the orbital wavefunctions take on more unusual shapes as they become more distorted. calculation errors can lead to asymmetric orbitals in otherwise symmetric molecules as computers have a limited number of decimal places with which they can operate and don't deal concepts like "1/3" as an exact number readily - this leads to compound errors
	the anti-bonding B 2s H1s orbital

2 - TlBr₃

introduction

to efficiently model TlBr3 Pseudo-potentials were used in order to decrease the computational load. This involves making the assumption that most of the bonding and interaction that the atom takes part in is due to the frontier atomic orbitals, and that those further down in energy contribute little more than an electrostatic interaction. This can be understood if we imagine that there are so many deep atomic orbitals that they essentially average out to be spherically symmetric. now a large number of electrons don't have to be considered individually and can be approximated as a force field.

For Thallium tribromide this is a useful assumption. both are large elements (81 and 35 electrons respectively) and thallium is expected to interact with sp2 type orbitals and bromine is expected to behave as a halide, with some possible influence from the lone pairs. In making these assumptions based on chemical intuition we imprint our expectations (of a D3h trigonal planar molecule) onto the calculation which imparts some bias, but saves a lot of computation time. For heavy atoms like thallium using pseudo-potential basis sets can actually improve accuracy, because pseudo-potentials can be designed which take into account relativistic effects which are prominent when an electron must 'orbit' so quickly that its speed becomes large enough for such effects to alter its mass, such as in gold.

for thallium relativistic contraction of the 6s orbital is sufficient to contribute to the inert pair effect. this makes the fomation of heavier thallium trihalides unfavourable, as the bond enthalpy decreases to the point whereby there is not sufficient energy to promote the 6s electrons into sp2 orbitals.

optimisation

the calculation was carried out with the RB3LYP:LANL2DZ method. Frequency and NBO analysis were carried out on top of the optimisation, with the point group of the molecule defined as D3h. LANl2dz is a medium quality basis set.

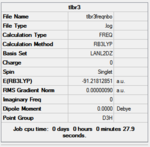
the frequency analysis and NBO analysis were carried out using the same method and the same basis sets as for the optimisation. If different basis sets were used then the frequency analysis would be wildly incorrect: within a method and basis set the electronic structure of the molecule is calculated to be self-consistent, but this might not be self-consistent under another method. furthermore the energies calculated by different methods are different, and might use different gaussians. the frequency analysis functions by calculating the potential energy surface around the atoms and then calculating how they would move around on that potential surface and how the potential surface would change in response to movement of the atoms. a frequency analysis is therefore useful because if the optimisation hasn't reached an absolute minimum, then the frequency calculation might disturb it enough to find a better minimum. It is therefore important to check that the frequency analysis was successful.

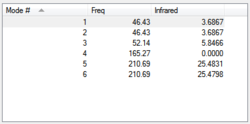
there are three negative frequencies, but as they are very close to zero (within the calculation error of +/- 10cm^-1) the frequency analysis is acceptable.

The reference values for Tlbr₃ IR absorption are 257w & 220vs. this agrees quite well with the calculated peak at 210.69cm^-1.

The molecule was constrained to D3h before optimisation on the assumption that the bromides and the thallium would form a trigonal planar structure, and programming in this structure before-hand would save considerable computation time. therefore the bonds were defined beforehand as 120o. The bond lengths optimised to 2.65A, which is much longer than the B-H bonds of 1.22A. Both Tl and Br are very soft and very diffuse. the literature value for their bond lengths is 2.52A, but this reference was taken using x-ray scattering for crystallised TlBr₃, so the discrepancy is acceptable.

Bonding

Gaussian draws bonds based on distance criteria, So for some heavier atoms in molecules it is possible that atoms are too far away for gaussian to draw a bond, or for some atoms bonds are drawn when clearly they are not to be expected.

In considering whether two atoms are bonded there are several criteria which i consider must be fulfilled to indicate a bond. Firstly, they should share electron density through space between them in phase in an occupied MO, with the degree of bonding described by the extent to which the MOs bridge the two atoms. A strong bond will have a great deal of electron density between the two. The two atoms should also have a vibration associated with them such as a stretch or a bending interaction. A stretch demonstrates that the two atoms have a repulsive interaction as they approach and an attractive interaction as they move apart. a bending vibration indicates that there is also an angular dependance, which indicates that the atoms are not merely attracted to each other at a particular range, but rather they are localised to a particular part of space with reference to the other atom. These criteria allow for bonding to be determined from computational results where the MOs are readily visualised and vibrations easily assigned, even if distance criteria don't apply.

NBO

Because bromine is more electronegative than thallium, and thallium has large diffuse orbitals which are easily polarised, it is expected that there will be bond polarisation toward bromine.

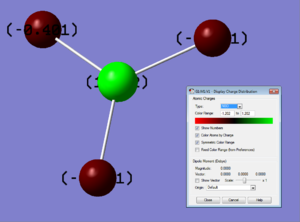
With a charge of -0.4 on bromine and +1.20 on Tl there is clearly a significant redistribution of electron density.

   Atom  No          Natural Electron Configuration
----------------------------------------------------------------------------
    Tl    1      [core]6S( 1.22)6p( 0.59)7p( 0.01)
    Br    2      [core]4S( 1.96)4p( 5.44)
    Br    3      [core]4S( 1.96)4p( 5.44)
    Br    4      [core]4S( 1.96)4p( 5.44)

Analysis of the output file gives this data^ which shows that the Tl has 40% of its electron density from the 6s and 6p orbitals spread onto the bromines. because they have shared equally, they must be equivalent, confirming that thallium bromide has hybridised 6sp2 orbitals with which it is bonding to bromine.

3 - Cis and trans Mo(CO)₄(PPh3)₂

Molybdenum tetracarbonylditriphenylphosphine is of the type M(L)₂(L')₄, which gives it two possible isomers cis and trans. the two different isomers have subtle but important differences in the number and type of vibrational modes, and their are important steric contributions.

In this section the triphenylphosphine ligands will be replaced by trichlorophosphine ligands because they share similar electronic donation characteristics. This allows the relative energies to be approximately modelled, but will give also give useful information about the vibrational modes. they don't however have identical steric bulk. one of the important features of triphenylphoshine is its large steric cone angle of 145^o compared to 124^o for pcl₃. this is likely to dramatically effect the validity of the results.

relative energies

Relative energies:

cis	trans
/	+10.508kj/mol
cell	cell
CIS	TRANS

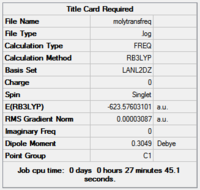A difference of 10.5kj/mol is not large, and is close to the error margin for the calculation methods used for this basis set. This is especially the case because specific functions for Phosphorous haven't been used. This amount of energy would readily interconvert at room temperature.

the cis isomer is more stable for the system studied. this is qualitatively because the phosphine ligands are sigma donors, and are increasing the electron density at the molybdenum center, which is then readily distributed to the pi-acceptor carbonyl ligands. this explains the lower stretching frequencies of the carbonyl ligands observed in the vibrational analysis. in the trans isomer the phosphines are not interacting significantly with any d-orbitals on molybdenum with the correct symmetry to redistribute that electron density into the π* orbitals of CO. The C=O bonds are generally shorter in the cis isomer for this reason; the trans effect is increasing the strength of both the Mo-P bond and the Mo-C bond at the cost of the C=O bond.

the increased cone angle of real triphoshene ligands Is likely to raise the energy of the cis compound greater than the trans compound. For trans phosphines even with large ligand cone angles the carbonyl ligands can exist in a belt between the two ligand steric cones. for the cis compound this is not the case.the two steric cones touch on one edge, and opposite this edge two carbonyls must crowd into only 70^o of space. the other two carbonyls on the other hand have plenty of room.

To force the complex to form a cis geometry there are a number of simple steps which could be undertaken, such as the use of bidentate bridged phosphate ligands which force a certain bite angle onto the metal. phosphorous triols could form hydrogen bonding interactions that help hold the two phospines in a cis configuration.

the cis configuration allows each of the phosphines to be trans to one carbonyl, which is a pi acceptor. in order to make the most out of the trans effect the phosphines should be as electron donating as possible (hydroxyls are moderately donating making them a good option). a good alkyl donating group would be isopropyl, which has a good balance between donating strength and steric bulk. p(tButyl)3 would likely be too bulky as it has a cone angle of 182^o, making it hard to guess whether any preference would be shown. it would likely not be able to attack the metal center twice due to its large size, as more carbonyls would have to leave, giving the metal too few electrons.

To increase the affinity for the trans complex the phosphine ligands should be very weak donors, so withdrawing groups such as carbonyl groups, fluorides or phenols would be useful.

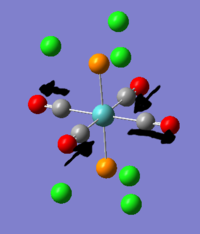
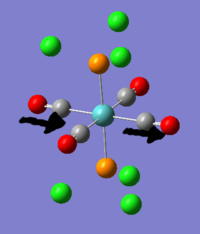
Vibrational analysis

Vibrational analysis - trans

wavenmuber/ cm-1 , (Abs)	Assignment	image
2031.16 , (3.76)	this is the symmetric stretch for all four carbonyl ligands simultaneously. there is no dipole change and therefore the absorbance is very low
1977.4 (0.635)	this is the symmetric stretch for trans pairs, with each pair stretching out of phase. again there is no change in dipole so the expected and observed absorbances are both very low.
1951.11 (1466)	this is the asymmetric stretch for each of the pairs of trans carbonyls. this stretching is degenerate and is the only carbonyl with a changing dipole, giving it the high absorbance.

spectrum Expected bands: 1 found: ~1. The two symmetric stretches at 2031 and 1977 should have had 0 absorbance. whilst they were >500x smaller than the 1951 peak, they weren't 0. the molecule could have had its point group constrained to D2h for this calculation, which might have removed some of the distortion. The actual trans C-Mo-C angle in the complex is not perfectly 180^o so it is reasonable that there should be a slight absorbance.

Vibrational analysis - cis

wavenmuber/ cm-1 (Abs)	Assignment	image
2023.24 (597.9)	Symmetric stretch for all the carbonyl ligands. large change in dipole from the two cis carbonyls therefore large absorbance.	I did the arrows like that because i thought you would get bored if you spent all week marking nice arrows and if you had some that were hand drawn with the calligraphy brush on photoshop and then you read this comment then you might not be so bored.
1958.3 (632.44)	semi-symmetric stretch: trans carbonyls are symmetric with the cis carbonyls stretching together in the opposite phase. Again the cis carbonyls contribute to the large absorbance.
1948.58 (497.9)	large asymmetric stretching of the trans carbonyls coupled to a lesser degree of symmetric stretching of the cis carbonyls
1945.26 (763.2)	large asymmetric stretching of the cis carbonyls and of the trans carbonyls to a lesser degree.

spectrum

Without mixing: expected 3, found 4: if the vibrations don't mix then the trans carbonyls symmetric stretch shouldn't be visible. viewing the vibrations on gauss it is obvious that the two trans carbonyls do not vibrate alone, the neighbouring cis-related carbonyls join them. the cis carbonyls will always result in an absorbance when they participate because they always break symmetry and change the dipole.

The trans carbonyls have a c-Mo-C bond angle of 178^o so even without mixing there is to be expected a very low absorbance peak. it is this 178^o symmetry break that allows them to mix.

The stretches of the cis ligands are notably lower than the stretching frequencies for the trans carbonyl ligands. This is due to the trans effect: the phosphines are donating into the CO pi* orbital and decreasing the strength of the bond. this is only observed to a lesser degree for the totally trans complex because the orbitals that bond the carbonyls are largely orthogonal to those interacting with the phosphines. this allows the carbonyls to stretch as trans pairs largely independent of the other trans pair in the molecule. For the cis complex there is considerable mixing of the vibrational modes, because different combinations of each ligand might be interacting with any one orbital, which helps 'conduct' the vibrations around the molecule.

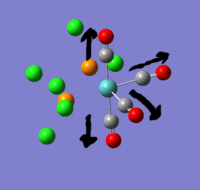
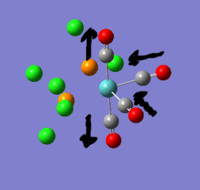
Both the Cis and trans molybdenum complexes exhibited some particularly low frequency vibrations. These are due not to the vibration of individual atoms or bonds, but due to the movements of entire groups. the two lowest from each are shown and described below.

Low frequency vibrations

Complex and wavenumber/cm-1	gif image	description
trans, 5	clickthrough	PCL3 symmetric twisting (with Mo(CO)4 twisting the opposite direction)
trans, 6	clickthrough	PCl3 antisymmetric twisting
Cis, 10	clickthrough	PCl3 symmetric twisting
cis, 17	clickthrough	PCl3 antisymmetric twisting

For those vibrations with particularly low energy it is likely that there are multiple hot bands in the spectrum. typical vibrational transitions follow the selection rule (Δn=⁺/_-1), and at 300K only the first and fundamental vibrations are populated to any degree. As the energy of the transition decreases however there is an increased population at n=1,2 and some absorption for the n(1-->2) transition is observed. this hot band is red-shifted (at lower wavenumber) because higher vibrational levels are closer together due to anharmonic effects.

LITERATURE COMPARISON

IN THE LITERATURE there is some data on a similar compound, differing in that it has PPh₂(NHPh) ligands. these are likely to have a similar steric bulk to the PCl₃ ligand (P(OPh)3 has nearly identical cone angle to PCl₃) although they will behave as if they are better electron donors than PCl3. However, the comparison is overall fair.

literature comparison

property	Computed	literature
Cis P-Mo-P bond angle/o	87.06	95
Cis vibration frequency	see above	"1870 to 2025"

The cis values are in reasonable agreement with the literature values, although the appropriateness of the literature source is questionable.

4 - Mini Project - Gold and silver clusters and their coordination with bromomethane

Introduction

In this paper the authors produce gold and silver clusters containing 1,3,5 and 7 atoms with a +1 charge using a mass spectrometer and trapped them for timescales up to 5s. this was sufficient to introduce an atmosphere containing small partial pressures of bromomethane, allow the clusters to react, and then send them to the detector to analyse the products. The authors found that the clusters were able to successfully catalyse the breakdown of bromomethane into methyl radicals and form ethene, and this reaction was promoted by 266nm irradiation. they also found that silver clusters were effective, but that they decomposed upon irradiation.

In this project the bonding and structures in some of the clusters and complexes will be computed and compared with the hypotheses about the cluster structure in the paper, with a view to understanding the way in which the cluster ions interact with the bromomethane.

direct link to paper

Problems to analyse

1. What form do the bromomethane Gold coordination clusters take? how does the bromomethane interact and what effect does the interaction have on its electron distribution? does this explain the observed reactivity?
2. How do the silver clusters differ from the gold clusters and why? why do the silver clusters decompose during the irradiated reaction?
3. The authors discover that the maximum number of bromomethane that can coordinate to Au5+ is 4. Their hypothesis is that the Au₅+ forms a cross. Is this true? what is the computed structure?

In order to solve these problems The compounds will be simulated using pseudo-potentials. Frequency analysis will be carried out to check that the structures have converged and to gain information on bond strengths along with the NBO calculations.

The Au3+ and clusters will be the focus of this project, as they are more structurally interesting than the Au+ or Ag+ naked cation, but require less computation time than the larger M₅+ and M₇+ complexes. simulation will be carried out for M₃(MeBr)_n⁺ where M=Ag,Au & n=0-3, with analysis focusing largely on the gold complexes, with comparisons to the silver complexes as necessary.

1. structure and bonding in the clusters

The Au₃+ and Ag₃+ were optimised to determine their structure, which was predicted to be of D3h symmetry. this was verified by the calculations, and frequency analysis confirmed the minima. all three metal atoms had equal charge of +0.33 and were otherwise identical. the symmetric stretch frequencies of the two clusters were also calculated to be practically identical at 170cm^-1 for au₃+ and 167cm^-1 for ag₃+. the gold cluster had bond lengths of 2.68A similar to 2.75A for the Ag₃+ cluster. literature values for gold-gold bond lengths in nanoparticles are notably smaller than in bulk gold (2.88A for bulk, 2.72A for an 8A particle corresponding to roughly 7 to 13 atoms) so the computed value is excellent.

Au3+ and Ag3+ cluster orbitals

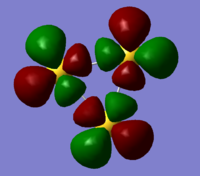
Orbital	HOMO	Homo-1	Homo -2 (7 fold degenerate)
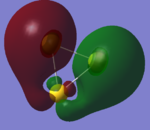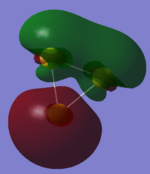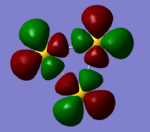image				File:STOWau3homo1.PNG
analysis	two antibonding 6s orbitals participating in a bizarre bonding interaction with a dxy orbital. has two sigma acceptor sites and a pi acceptor site	a 6s orbital antibonding to two bonding d orbitals. this orbital is a sigma acceptor at the corners	comprised of two dxy orbitals and one dx2-y2 this orbital is fully antibonding and has a good deal of electron density pointing out toward the corners making this an excellent HOMO.	three dzx orbitals in a fully bonding mode, this orbital doesn't provide opportunities for interaction.

On Bromomethane

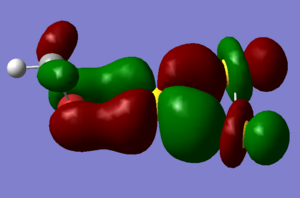
To understand the chemistry of the clusters it is important to note that in methyl bromide the bromine has only a slight negative charge, with the carbon carrying -0.54eV. The interaction with the gold clusters is a HOMO-LUMO interaction. bromine carries most of the electron density of the π* HOMO orbital, which might cause it to be the coordinating atom, but there are several other possible frontier orbitals which don't present a p-type orbital to the gold cluster. The LUMOs of the gold cluster present either s-type or p-type sites for the bromine, so the actual interaction is probably a mixture of several interactions which lead to the formation of a bent 105^o C-Br-Au bond angle, and a small reduction in the negative charge on bromine without concomitant loss of electron density at carbon. What is for certain is that the bromine is the nucleophile, and that there is considerable orbital mixing. for example the Au₃+ HOMO-15, composed solely of dz² orbitals, contributes to the lowest energy MO in Au₃(MeBr)₃+ which shows delocalisation over both a methyl bromide and the gold atoms. because Gold has so many atomic orbitals (a full complement of 5d orbitals) close in energy combining to form a range of different gold cluster MOs, rationalising which orbitals have interacted is difficult.

MeBr Homo orbitals

Orbital	HOMO	HOMO-1	HOMO-2
energy	-0.2815	-0.2815	-0.3894
type	π* orbital. will bond via Br via a π bond	degenerate. at 90o to previous	σ bond formed by two pAOs. will form a σ bond at Br
image

MO Diagram compared to computation

To form the MO diagram it was assumed that the occupied 5d orbitals were much lower in energy than the 6s orbitals, so the MO diagram looks like that for H₃+. this was then interacted with the MOs from Bromine in MeBr, to give an approximate guess. It should be noted from the calculation done for Au₃+ that the Gold FMOs do contain a d-orbital contribution from the antibonding d-orbitals, which are able to interact with the pi* orbitals on MeBr when the Gold 6s orbitals have different symmetry.

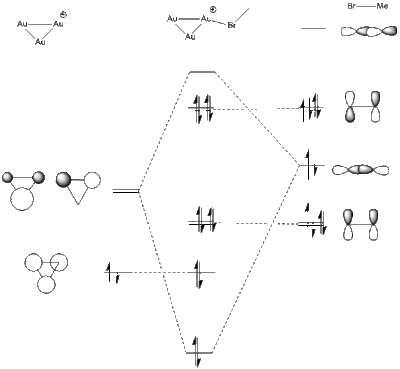
It is possible to find the orbitals that have interacted in the output from the calculation

interaction

HOMO - MeBr	LUMO - Au3+	forms MO Au3MeBr+

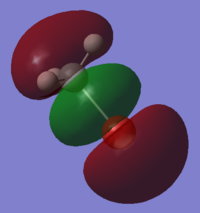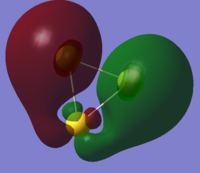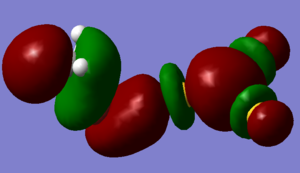In fact what is found is that the MeBr has not bonded as expected by the simple MO diagram and has changed its angle of alignment to 105o in order to be able to sigma bond with its pi bonding orbital. this gives the p-p sigma bond a twisted geometry and makes it difficult to recognise. instead of bonding to the predicted s-bond orbitals the bond has actually been formed with a collection of dz² orbitals.

There are also some MOs near the level of the gold LUMO which are formed by d-orbitals. adding these to the diagram and mixing them with the pi* orbitals affords a more complicated MO diagram. did the calculation produce this orbital as predicted?

interaction

HOMO - MeBr	LUMO - Au3+	forms MO Au3MeBr+
cell

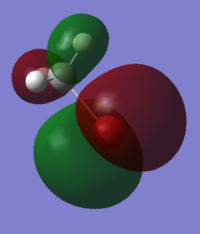In this case again the interaction is not with the predicted orbitals exactly, but it is still a dxy orbital. It is entirely possible that when the new calculation was submitted ab initio that the program found a different ordering of the orbitals, rather than taking the pre-calculated orbitals for each and combining them as i have done.

So the calculations do agree roughly with the MO diagrams we can predict, but the calculation is able to find mixing contributions better than we are able to guess, and the calculation is also able to quantitatively assign the energies to each MO based on how much it calculates they mix and how much the mixing reduces the energy.

Clusters

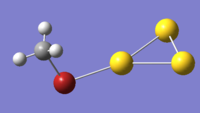
the authors hypothesise that the MeBr molecules bond by the bromine atom and that they probably remain in plane. the simulated clusters did bond via the bromine, but they did so at an angle of 105.2o bent above the plane of the gold cluster. this gives the bonding the appearance of a lewis lone pair interaction. the calculation was also initiated with the carbon closer to one of the Gold atoms than the bromine. this scenario eventually finished at a local minima with the bromine closest to the gold and the methyl stuck the other side of the Au3+ plane, confirming that the bromine is the nucleophile and there is a tendency to form Au-Br-C bond angles which are near the tetrahedral ideal. The effect of the Interaction is to slightly decrease the amount of positive charge on all the gold atoms almost equally, the atom bonded to bromine is only slightly less positive. the Methyl group is largely unchanged at +0.54eV. this is likely the cause of the increased ability of the bromomethane to undergo homolytic bond cleavage when

coordinated: the bromine has a slight positive charge (+0.1eV) and is coordinated to atoms with large delocalised orbitals which are ready acceptors. it is not much of a stretch for the electron density to be transferred just a little bit more to the Au3Br part of the complex, perhaps as part of a vibration, and the bond is formally cleaved and there is an entropic payback from the release of the methyl radical (which is reported to form ethane, contributing an overall decrease in gibbs energy).

Upon bonding of two MeBr molecules the structure has become a little more complicated. now both MeBr molecules bend in opposite directions above and below the plane, and away from each other. This steric contribution is unlikely to be major as the two methyl groups are considerably distant from each other ~4A. there is a further decrease in the positive charge on gold and again the charge is well distributed, with both bromines having a slight positive charge.

the ability of the complex to accept extra electron density might be expected to be diminshed on addition of more MeBr molecules, but the authors found that this was not the case, and that when the reaction time was increased steadily to 5s there was in increase in poly-coordinated compounds followed by a decrease in the mono-coordinated species, then an increase in species that were coordinated to up to 3 product ethene molecules whilst still retaining one MeBr. Evidently the rate of complex formation is slow, but the formation of the poly-coordinated clusters suggests that the mono and di-coordinated compounds are stable to decomposition and that only with the addition of the third bromomethane is there a tendency to decompose. This indicates that the coordinated bromomethane is interacting with its neighbour via a radical reaction. The disubstituted cluster cannot interact because the two MeBr are pointing on opposite faces of the ring. on addition of the third MeBr it is forced to be on the same side as another MeBr. the two react to form ethene and possibly HBr. The ethene remains coordinated to the gold, and more MeBr molecules coordinate. The authors state that irradiation of the complex at this stage reformed the gold complex. this is likely due to the excitation of LMCT or M-M bands which disrupt the bonding of the ethenes. The gold is able to withstand this because its bonds are almost twice as strong as those in silver.

2. Silver Clusters compared to Gold Clusters

Frequency analysis for M3+

cluster	wavenumber/cm-1, abs	force constant	assignment
Au3+	107.6, 0.65	1.34	E1' (C2v, Cs) degenerate vibrations
Au3+	170.83, 0	3.38	A1' (D3h) symmetric ring stretch. no absorbtion as there is no change in dipole
Ag3+	110.7, 1.67	0.77	E1' (C2v, Cs) degenerate vibrations
Ag3+	167.52, 0	1.77	A1' (D3h) symmetric

the vibrational frequencies of the two complexes are almost indistinguishable. checking the gaussian output file, the force constants indicate that whilst the reduced masses for the vibrations have doubled, the force constants have also doubled so the vibrations are very similar. The increased force constant for the gold might explain the shorter Au-Au bonds in the uncoordinated cluster, and explain why the gold complex doesn't decompose in photochemically promoted radical formation reactions. it takes more energy to disturb the gold atoms due to their large mass and they have stronger bonds, making them more stable than the silver cation trio.

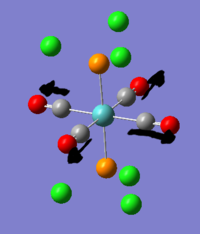
3. Au5+ structure

Au5+ was optimised and gave a D2h structure. this allowed the cluster to keep its bond lengths of 2.65A(edge) and 2.75A (center to edge) which are similar to those found in the D3h triangular structure. the D4h structure would have higher symmetry than the D2h structure but the cost would be the loss of interactions between the edge gold atoms which would now be unable to interact because they would be too far apart at around 4.5A. the 7-membered cluster is hypothesised to form a 6-membered ring with a gold atom at the center, which would maximise all the interactions: 6Center-peripheral and 6 edge interactions.

This information indicates that the methyl bromide must bond to a gold atom which is as exposed as possible. Catalytic activity of nanoparticles is known to increase with decreasing size for some reactions for this reason. Large nanoparticles have fewer exposed sites per atom, so are less efficient.

The NBO analysis shows that the peripheral gold atoms are able to have a good positibe charge and are thus catalytically active, by the gold in the centre has an unprecedented negative charge on it. This explains why the central gold atom is totally unable to coordinate.

Conclusion

The Positively charged gold nanoparticles likely function by withdrawing electron density from the bromides, leading to homolytic bond cleavage. this occurs because The gold clusters present large orbitals of varying types which offer opportunities for the radicals to delocalise. The many available occupied and unoccupied orbitals in the gold cluster present a range of symmetries and energies which present many options for the products of the reaction to interact with, which helps lower the overall reaction pathway.

the transition state for the homolytic cleavage involves transfer of electron density away from the C-Br bond and on to bromine. normally this would be high in energy, but the gold cluster facilitates this pathway. the high energy products are then also free to interact, lowering their energy, until such a time as they can rearrange into ethene

Larger clusters are probably less effective because they offer fewer sites per atom and the reactants, although this might aid the formation of products as the radicals produced are in closer proximity and might be more able to react to form the final non-radical products of the reaction. There is also significantly less positive charge per atom in larger clusters, making the cluster less able to withdraw electron density and makes the formation of the Br- counterion less energetically favourable

DSPACE

moly trans [click http://hdl.handle.net/10042/to-9930]

moly cis [click http://hdl.handle.net/10042/to-9931]

ag with (n) MeBr 1 [click http://hdl.handle.net/10042/to-9945]

2 [click http://hdl.handle.net/10042/to-9735]

3[click http://hdl.handle.net/10042/to-9925]

au with (n) MeBr 1 [click http://hdl.handle.net/10042/to-9929]

2 [click http://hdl.handle.net/10042/to-9928]

3 [click http://hdl.handle.net/10042/to-9926]

Au₅ [click http://hdl.handle.net/10042/to-9927]