Jump to content

Rep:Mod2:man7286

From ChemWiki

Introduction

This lab uses computational techniques to calculate various properties of small inorganic molecules, ranging from bond lengths and angles to IR spectra and molecular orbitals. The structures of the molecules were drawn using Gaussview5 or ChemBio3D Ultra. Calculations were performed by Gaussian and the results analysed through Gaussview5.

BH3

Geometry Optimisation[1]

Figure 1: Geometry Optimisation Results for BH3

The method and basis set used for the geometry optimisation of BH3 were B3LYP/3-21G, this is a relatively low accuracy basis set. The optimised bond length was 1.19 Å and the bond angle was 120.0°. Both these parameters agree exactly with the literature[2]. Figure 1 shows the summary of results from the calculation, the optimised energy for the molecule is -26.46 Eh.




.

Molecular Orbital Analysis[3]

Figure 2: MO Diagram of BH3

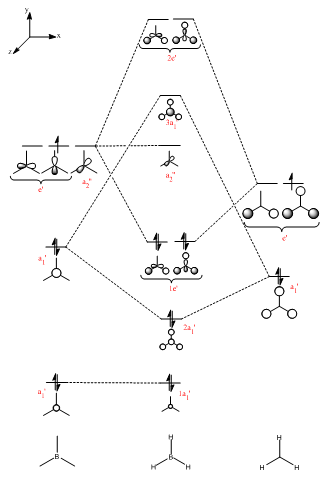
The shape of the orbitals in the MO diagram for BH3 were predicted using LCAO theory and the relative energy levels were estimated.

Table 1: Comparison of LCAOs with Calculated MOs
Occupied Unoccupied
Calculated MO Energy Orbital LCAO Calculated MO Energy Orbital LCAO
-6.73049 1a1' -0.07458 1a2"
-0.51765 2a1' 0.18859 2e'
-0.35681 1e'
0.19192 3a1'
Figure 3: Modified MO Diagram in Response to Calculated MOs (Affected Area Shown Only)

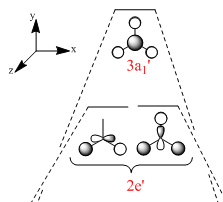
Figure 2 shows the predicted MO diagram for BH3. Table 1 shows the calculated MOs for the molecule. The calculated MOs were tabulated in ascending order of energy and the corresponding LCAO was matched to it. Most of the calculated LCAOs are in the same order as on the MO diagram. The only exception is that the 3a1' orbital was calculated to be higher in energy than the 2e' degenerate pair, whereas I predicted it to be lower in energy. The correction to the diagram is shown in Figure 3. The shape of the calculated MOs match up well to the predicted LCAOs, showing that qiualitative MO theory can be very useful in predicting the shape of the molecular orbitals.

Natural Bond Orbital Analysis[3]

Figure 4: Charge Distribution in BH3

NBO Charges: B = 0.33, H = -0.11

Figure 4 shows the charge distribution and NBO charges for the BH3 molecule. The light green colour of the boron atom shows that it is strongly positively charged. This is to be expected as boron has an empty p orbital, making it a Lewis acid.

Figure 5: Excerpt from log file showing the nature of the bonding

NBO analysis is also used to determine the nature of the bonding in the molecule. Figure 5 shows that there are three sp2 bonds, each containing two electrons, and one lone pair with mainly s charachter, also containing two electrons. It also shows that slightly more of the electron density of the bonds lies on the hydrogen atom, which further explains the positive charge on the boron atom.

Frequency Analysis[4]

Figure 6: IR Spectrum of BH3
Table 2: Summary of Vibrations of Trigonal Planar BH3
Image of Vibration Description Frequency/cm-1 Intensity D3h Point Group
1 All 3 B-H bonds bend out of the plane of

the molecule in the same direction

1146 93 a2"
2 Bottom H-B-H bond bends inwards equally

towards eachother

1205 12 e'
3 Top B-H bond bends to the left, bottom 2

B-H bonds bend equally (but less movement) anti-clockwise

1205 12
4 All 3 B-H bonds strecth equally outwards

in the plane of the molecule

2593 0 a1'
5 Bottom 2 B-H bonds stretch asymmetrically

in the plane of the molecule

2731 104 e'
6 Bottom 2 B-H bonds stretch together and

top B-H bond stretches asymmetrically

2731 104

Table 2 shows the six vibrations of the planar BH3 molecule, but the IR spectrum in Figure 5 only shows three peaks. This can be explained by the data in the table. Vibration 4 is the in-plane symmetric stretch of the 3 B-H bonds, therefore the overall dipole of the molecule doesn't change so the intensity of the vibration is 0. Vibrations 2 & 3 and 5 & 6 are degenerate pairs so the two vibrations form a single peak.

TlBr3

Geometry Optimisation[5]

Figure 7: Summary of TlBr3 Optimisation Results

The method and basis set used was B3LYP/LanL2DZ, which is a medium accuracy basis set. The optimised bond length was 2.65 Å and the Br-Tl-Br angle was 120.0°. The literature bond length is 2.56 Å[6] therefore the difference between experimental and calculated is 0.09 Å. The calculation is therefore in good agreement with the literature.

Frequency Analysis

The same method and basis set must be used for the original optimisation and the frequency calculation so that both calculations are at the same level of accuracy. Frequency analysis must be carried out because the optimisation is based of the first derivative of the potential energy curve, therefore it only picks a point where the gradient is zero i.e. the graph is at a maximum or minimum. Frequency analysis performs a second derivative on the potential energy curve. The analysis is performed on the optimised file therefore where the gradient is zero. If the second derivative is positive this point is a minimum and if negative the point is a maximum. The frequency analysis is therefore carried out to ensure that the optimised geometry is at the energy minimum.

Table 3: Summary of Low Frequencies, from TlBr3 Log File
Low Frequencies
-3.4226 -0.0026 -0.0004 0.0015 3.9361 3.9361
46.4288 46.4291 52.1449

The first row of low frequencies represent the motions of the centre of mass of the molecule. Essentially they form the "-6" term in the 3N-6 equation, which determines the number of vibrational modes in a non-linear molecule where N is the number of atoms. Ideally these should all be zero, but due to experiment error they normally lie within ±10 cm-1. The frequencies in the second row represent the vibrational frequencies of the molecule and must all be positive. The fact that these all are means that the calculation has found the correct minimum energy.

Figure 8: IR Spectrum of TlBr3
Table 4: Summary of Vibrations of TlBr3
Frequency Intensity Point Group
46 4 e'
46 4
52 6 a2"
165 0 a1'
211 25 e'
211 25

Lit. stretches are 257, 220 cm-1[7].

Again, there are six vibrational modes for TlBr3 but only three peaks on the IR spectrum, Figure 7. One vibration is not IR active and there are two degenerate pairs. The frequencies are much lower for TlBr3 than BH3. This is because the bonds are longer and therefore weaker. Also, the e' vibration is lower in energy than a2" whereas in BH3 it is higher in energy.

Isomers of Mo(CO)4L2

Figure 9: Isomers of Mo(CO)4L2

The method and basis set used for the following optimisation and frequency calculations was B3LYP/LANL2MB.

In this exercise the optimised geometries and IR spectra for cis- and trans- isomers of Mo(CO)4L2 were calculated and compared. The main focus was the number and frequency of carbonyl stretches. The length of the C-O bond in cabon monoxide is 1.128 Å and the stretching frequency is 2143 cm-1[8]. There are two types of bonding between the CO ligand and a metal: σ-donation and π-back bonding.

Figure 10: Diagram showing the bonding in carbonyl ligands

In σ-donation electrons are donated from the carbon p orbital to a relavant orbital on the metal. In π-back bonding electrons are donated from a d orbital on the metal to the π* orbital on the carbon. Donation into this orbital weakens the CO bond and therefore lowers the carbonyl stretching frequency.

cis-Mo(CO)4(PCl3)2

Geometry Optimisation[9]

energy = -617.52 Eh

Table 5: Comparison of Optimised Geometries to Literature Values[10]
Bond Length/Å Literature Value/Å Bond Angle/° Literature Value/°
Mo-C (axial) 2.11 2.041 C-Mo-C (axial) 177.9 174.1
Mo-C (equatorial) 2.06 1.972 C-Mo-C (equatorial) 89.0 83.0
Mo-P 2.53 2.577 P-Mo-P 93.0 104.62
C-Mo-P (axial) 177.3 163.7
C-Mo-P (equatorial) 89.7 80.6

The values are all close to the literature values, within experimental error (~10%).

Frequency Calculation[11]

Figure 11: IR Spectrum of cis-Mo(CO)4(PCl3)2

energy = -617.52465357 Eh

Table 6: Summary of C=O streches in cis-Mo(CO)4(PCl3)2
Frequency Intensity Vibration Description
2108 152 Equatorial C=Os asymmetric stretch
2114 237 Equatorial C=Os symmetric stretch, axial C=Os asymmetric stretch
2114 263 Equatorial C=Os symmetric stretch, axial C=Os asymmetric stretch
2143 148 All C=Os symmetric stretch

The literature CO stretches for cis-Mo(CO)4(PCl3)2 are 2070 and 1987 cm-1[12]. The calculated values are within experimental error but there are three carbonyl peaks on the predicted spectrum and only two in the literature.

trans-Mo(CO)4(PCl3)2

Geometry Optimisation[13]

energy = -617.52

Table 7: Comparison of Optimised Geometries to Literature Values[14]
Bond Length/Å Literature Value Bond Angle/° Literature Value
Mo-C 2.11 2.011 C-Mo-C (trans) 179.7 180.0
C=O 1.19 1.165 C-Mo-C (cis) 90.0 92.1
Mo-P 2.48 2.500 P-Mo-P 179.0 180.0
C-Mo-P 90.0 89.6

Frequency Calculation[15]

Figure 12: IR Spectrum of trans-Mo(CO)4(PCl3)2

energy = -617.52206254 a.u.

low frequencies: -0.0002 0.0005 0.0006 4.2294 4.7994 8.7431 9.3212 14.1821 29.9911

Table 8: Summary of C=O Stretches in trans-Mo(CO)4(PCl3)2
Frequency Intensity Vibration Description
2110 286 2 trans C=Os asymmetric stretch
2111 284 other 2 trans C=Os asymmetric stretch
2126 1 trans-C=Os stretch symmetrically, asymmetrically to other trans-pair
2146 0 all 4 C=Os symmetric stretch

lit. IR 1953, 1896cm-1[16]

Conclusion

NOTE: In the gaussian files produced from the calculations there were no bonds present between the P and Cl atoms. This is because
the optimised bond length is longer than most organic bond lengths so the gaussian program doesn't put a bond between the atoms. 
When converting to .mol files on ChemBio3D Ultra I added bonds between the P and Cl atoms, this did not affect the geometry of the
molecule.

The axial Mo-C bonds on the cis isomer and all the Mo-C bonds on the trans isomer were calculated to be the same length, the equatorial bonds are 0.05 Å shorter. This is because they are trans to the PCl3 group therefore the metal is donating less of its electron density to the phosphorus atom, meaning there is more being donated to the carbon atom so the bond is shorter. The donation of electrons from the metal to the carbon goes into the π* orbital of the C-O bond, therefore weakening the C-O bond. This explains why the equatorial C-O stretches have a slightly lower frequency than the axial/trans isomer stretches.

IR spectroscopy is a good way to distinguish between the two isomers as the cis isomer has four IR active carbonyl stretches and the trans isomer only has two. This is because two of the carbonyl stretches in the trans isomer are symmetric so the overall dipole moment of the molecule doesn't change, i.e. they are not IR active. The trans isomer also has fewer peaks in the IR spectrum because it has a higher order of symmetry than the cis isomer, therefore more trans stretches are symmetrical and therefore IR inactive.

The cis isomer is more stable as it is lower in energy by 0.002591 Eh, 6.8 kJ mol-1. This energy difference is very small, it is the same order of magnitude as the energy available at room temperature, therefore the two isomers will rapidly interconvert at room temperature.

Mini Project: Al2Cl6

The method and basis set used for all optimisation and frequency calculations was B3LYP/6-31G.

Al2Cl6

Optimisation

Al2Cl6 Optimisation Log File

energy = -3246.320 Eh

Frequency

Figure 13: IR Spectrum of Al2Cl6

Al2Cl6 Frequency Calculation Log File

low frequencies: -5.8229 -5.6361 -0.0035 -0.0025 0.0028 2.6199 21.6041 51.6546 85.1422

Table 9: Summary of Vibrations of Al2Cl6
Frequency Intensity Vibration Type
22 0 Bridging Al-Cl-Al bonds bend out of plane, exterior Cl-Al-Cl groups rock symmetrically in plane, Al stationary
51 0 Exterior Cl-Al-Cls twist asymmetrically out of plane
85 0 Exterior Cl-Al-Cls bend symmetrically in plane
99 0 Bridging Cls move asymmetrically out of plane
102 0 Exterior Cl-Al-Cls rock in plane, Als move
113 14 Al2Cl2 square moves up and down in plane, exterior Cls move down and up
124 25 Exterior Cl-Al-Cls bend asymmetrically in plane
145 0 Al2Cl2 square twists in plane
159 18 Bridging Al-Cl-Al bonds bend out of plane, exterior Cl-Al-Cl groups rock symmetrically in plane, Als move
199 0 Bridging Al-Cl-Al bonds bend in plane, exterior Cl-Al-Cl groups bend symmetrically in plane
222 0 Bridging Al-Cl-Al bonds bend asymmetrically, oppositely, in plane
277 103 Bridging Al-Cl-Al bonds bend asymmetrically, together, in plane
294 0 Bridging Al-Cl bonds stretch symmetrically
355 153 Bridging Al-Cl bonds stretch symmetrically on same side, asymmetrically to opposite side
437 365 Exterior Al-Cl bonds stretch symmetrically on same side, asymmetrically to opposite side
476 0 Exterior Al-Cl bonds stretch symmetrically on both sides
570 0 Exterior Al-Cl bonds stretch asymmetrically on same side, asymmetrically to opposite side
580 258 Exterior Al-Cl bonds stretch asymmetrically on same side, symmetrically to opposite side

MO and NBO Analysis

MO/NBO log file[17]

Table 10: Molecular Orbitals of Al2Cl6
Unoccupied Occupied
Calculated MO Energy Calculated MO Energy
-0.00476 -0.35198
-0.01082 -0.35370
-0.01550 -0.35488
-0.06939 -0.35736
-0.10155 -0.36223
-0.12237 -0.36435

Al2Cl4Br2

Table 11: Summary of Geometries and Energies
Al2Cl6 Al2Cl4Br2 Bridging Al2Cl4Br2 Geminal Al2Cl4Br2 Cis Al2Cl4Br2 Trans
Energy Difference from lowest energy isomer/kJ mol-1 n/a 0.244 0.460 0 0.165
Bond Lengths/Å exo Al-Cl 2.17 2.18 2.17 2.17 2.17
bridging Al-Cl 2.41 n/a 2.40,2.42 2.41 2.41
exo Al-Br n/a n/a 2.29 2.29 2.29
bridging Al-Br n/a 2.52 n/a n/a n/a
Bond Angles/° Bridge 93.6 89.6 92.8 92.5 92.7
exo Cl-Al-Cl 123.3 123.0 122.5 n/a n/a
exo Br-Al-Cl/Br n/a n/a 129.0 125.7 125.7

Bridging Optimisation log file

Bridging Frequency calculation log file

Bridging MO/NBO log file[18]

Geminal Optimisation log file

Geminal Frequency calculation log file

Geminal MO/NBO log file[19]

Cis Optimisation log file

Cis Frequency calculation log file low frequencies: -5.5122 -5.1026 -3.2210 -0.0105 -0.0057 -0.0057 13.1103 48.2344 72.1486

Table 12
Frequency Intensity Stretch
279 0 Bridging Al-Cl bonds stretch symmetrically
352 136 Bridging Al-Cl bonds stretch symmetrically on both sides
397 369 Exterior Al-Cl/Al-Br bonds stretch symmetrically on one side, asymmetrically to the other side
442 19 Exterior Al-Cl/Al-Br bonds stretch symmetrically on both sides
551 21 Exterior Al-Cl/Al-Br bonds stretch asymmetrically on one side, asymmetrically to the other side
562 232 Exterior Al-Cl/Al-Br bonds stretch asymmetrically on one side, symmetrically to the other side

Cis MO/NBO log file[20]

Trans Optimisation log file[21]

Trans Frequency calculation log file

Table 13
Frequency Intensity Stretch
278 0 bridging Al-Cl bonds stretch symmetrically on one side, symmetrically to other side
353 136 bridging Al-Cl bonds stretch symmetrically on one side, asymmetrically to other side
400 396 exterior Al-Cl/Al-Br bonds stretch symmetrically on one side, asymmetrically to other side
441 0 exterior Al-Cl/Al-Br bonds stretch symmetrically on one side, symmetrically to other side
552 0 exterior Al-Cl/Al-Br bonds stretch asymmetrically on one side, asymmetrically to other side
561 249 exterior Al-Cl/Al-Br bonds stretch asymmetrically on one side, symmetrically to other side

Trans MO/NBO log file[22]

Conculsion

The cis isomer is the lowest energy, most stable, isomer but the difference in energy between this isomer and the rest is very small so interconversion between the isomers occurs readily at room temperature. The interconversion happens because one of the bridging bonds breaks, the other bridging bond rotates and a new bridging bond forms between the new atom.

Figure 14: Diagram of Interconversion Mechanism

In general the Al-Br bond is longer than the Al-Cl bond by 0.12 Å, this is because the orbital overlap is weaker therefore the bond is weaker. Also, the bridging Al-X bonds are longer than the exo Al-X bonds (X=Cl,Br). This is because the bridging bonds are 3 centre-4 electron bonds.

Bridging Br atoms increase the length of the exo Al-Cl bond by 0.01 Å. Geminal Br atoms lengthen the bridging Al-Cl bond on that side by 0.01 Å, but shorten it by the same amount on the other side, therefore on average the bond length remains the same. Cis and trans Br atoms have no effect on the bridging or exo Al-Cl bond length. The bridging angle is decreased most by bridging Br atoms, by 4°. Cis Br atoms decrease the angle by 1.1°, trans by 0.9° and geminal by 0.8°. Bridging Br atoms don't affect the exo angle. Geminal Br atoms decrease the exo Cl-Al-Cl angle by 0.8° and increase the Br-Al-Br by 5.7°. Cis and trans Br atoms increase the exo angle by 2.4°.

The addition of cis and trans Br atoms decreases the stretching frequencies of the Al-Cl and Al-Br bonds. This is because the Al-Br bonds are weaker so in general have lower stretching frequencies.

The shown occupied MOs (HOMO to HOMO-5) all show that the electron density is on the chlorine atoms. Therefore they are electron rich and the aluminium atoms are electron deficient.

References

  1. ↑ BH3 Optimisation Log File
  2. ↑ K. Kawaguchi, J. Chem. Phys., 1992, 96, 3411 DOI:10.1063/1.461942
  3. ↑ 3.0 3.1 MO and NBO Calculation Published Data DOI:10042/to-7497
  4. ↑ BH3 Frequency Calculation Log File
  5. ↑ TlBr3 Optimisation Log File
  6. ↑ J. Glaser, G. Johansson, Acta Chem. Scand., 1982, A 36(2), 125 DOI:10.3891/acta.chem.scand.36a-0125
  7. ↑ J. Blixt, J. Glaser, J. Mink, I. Persson, P. Persson, M. Sandstroem, J. Am. Chem. Soc., 1995, 117 (18), 5089 DOI:10.1021/ja00123a011
  8. ↑ http://www.ilpi.com/organomet/carbonyl.html accessed 15:29 15/0./2011
  9. ↑ Geometry Optimisation Published Data DOI:10042/to-7571
  10. ↑ F.A. Cotton, D.J. Darensbourg, S. Klein, B.W.S. Kolthammer, Inorg. Chem., 1982, 21 (1), 294, DOI:10.1021/ic00131a055
  11. ↑ Frequency Calculation Published Data DOI:10042/to-7576
  12. ↑ S.L. Mukerjee, S.P. Nolan, C.D. Hoff, R. Lopez de la Vega, Inorg. Chem., 1988, 27 (1), 81 DOI:10.1021/ic00274a018
  13. ↑ Geometry Optimisation Published Data DOI:10042/to-7572
  14. ↑ G. Hogarth, T. Norman, Inorganica Chimica Acta, 1997, 254 (1), 167 DOI:10.1016/S0020-1693(96)05133-X
  15. ↑ Frequency Calculation Published Data DOI:10042/to-7577
  16. ↑ M. Ardon, G. Hogarth, D.T.W. Oscroft, J. Organ. Chem., 2004, 689 (15), 2429 DOI:10.1016/j.jorganchem.2004.04.030
  17. ↑ Published Data DOI:10042/to-7692
  18. ↑ Published Data DOI:10042/to-7693
  19. ↑ Published Data DOI:10042/to-7694
  20. ↑ Published Data DOI:10042/to-7695
  21. ↑ Published Data DOI:10042/to-7666
  22. ↑ Published Data DOI:10042/to-7696
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod2:man7286&oldid=815537"