Rep:Mod2:kr207Mini
Mini project based on Ga2Me4Cl2
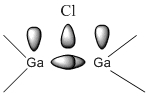
In this project a Ga2Me4Cl2 dimer was investigated.
With reference to the definition of bonds above, this compound is of particular interest as it forms unconventional 3c-2e bridging bonds. This was examined by looking at its molecular orbitals to get a better idea of the delocalisation of electrons in this compound. The strenght of these bridging bonds was also examined using IR data. The effect of changing terminal and bridging atoms was also studied, as explained in the following section.
Methodology and calculation settings
Changes were made to this starting compound for further structural and electronic examination.
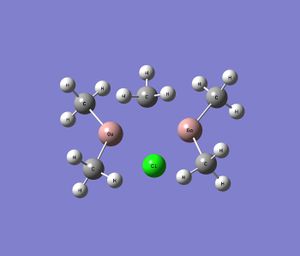
In Series 1 the effect of changing the bridging atom was investigated. First, the Cl was replaced by another halide, namely Br (Dimer2) to study the effect of a change within a periodic group. Then, then the bridging Cl in dimer 1 were replaced by Me-groups (Dimer4). The possibility of both Me and Cl as briding atoms in the same compound was also investigated (Dimer5).
In Series 2 the effect of changing the terminal substituents was investigated. The terminal groups were swapped with electron-withdrawing F-atoms (Dimer3) in constrast to the weakly electron-donating Me-groups in the starting Dimer1. To get a better idea of the influence of substituents, another dimer was computed where 2 Me-groups were replaced with Hs (Dimer6).
Table 1 below shows all dimers examined.
| Series 1 | 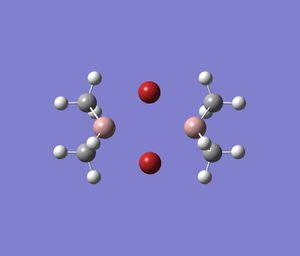 |
 |
 |
|---|---|---|---|
| Ga2Br2Me4 | Ga2Me2Me4 | Ga2MeClMe4 | |
| Series 2 | 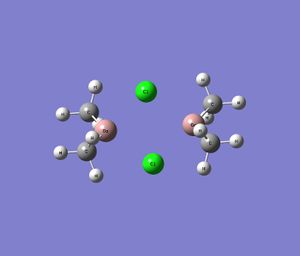 |
 |
 |
| Ga2Cl2Me4 | Ga2Cl2Me2F2 | Ga2Cl2Me2H2 |
Note that the images above show the geometry of the specific dimer after successful optimisation.
To study the effect of these changes on the bonding for all examples the bond length for the bridging 3c-2e bonds and the terminal 2c-2e bonds were measured. Furthermore, the terminal bond angles were determined and the distance between the 2 Ga-centers. This data was then compared across the 2 series. The key MOs were also established and computed for all compounds to get a better idea of the changes of electron-distribution for each compound.
Since the energies cannot be compared for different dimers, the corresponding monomers for each dimer were computed to determined the stabilisation of the dimer-structure relative to the monomeric structure.
For each dimer a frequency calculation was run to check the optimisation process as done for part 1. Key MOs were computed for all Dimers. For the starting Dimer 1 a detailed analysis of its MOs and vibrations was carried out.
It was initially tried to compute Dimer 4 with the Cl and Me in dimer 1 exchanged, i.e. 2 Me in the brdiging region and 2 Me and 2 Cl as terminal groups. Upon optimising however the Cl were also placed in the bridging position, as this seems to be the most realistic representation. Therefore, Dimer 4 was computed as above. Note that another option would be, when changing the terminal groups to replace as e.g. in dimer3 all Me-groups by F. However, initially it was also tried to optimised dimer4 with the 2 Cl-groups cis to each other, but this calculation failed to give the right bridging geometry. Therefore, for series 2 only 2 Me-groups were exchanged. The difficulty of forming Ga-Me-Ga bridges is evident from looking at the structure of dimer 4. This will be further commented on in the "Analysis"-section below.
Settings of optimisation calculations
All calcualtions for the optimisation process, the frequency analysis and the molecular orbitals were carried out using the same pseudo potential and basis sets: LANL2DZ. The electronic convergence was further increased by adding "int=ultrafine scf=conver=9".
In addition, Dimer 1 (DOI:10042/to-3158 ) and Dimer 4 were pre-optimised using the LANL2MB pseudo potential and the keyword-option: opt=loose. In short, using a low level basis set gave a good initial guess of the geometry of the compound.
However, using a higher level pseudo potential and specifying the additional keyword it was possible to reduce the total energy of all compounds further, giving a better approximation of the lowest possible ground state for each compound. This higher accuracy is also indicated by the lower RMS value for both geometries.
The geometry from this initial optimisation process was then further improved using LANL2DZ and refined additional keywords.
For Dimer 2, Dimer 3 and Dimer 5 were optimised based on these previously optimised dimers.
It was found that even though the optimisation was fully converged and optimisation and frequency analysis gave the same energy for the compound, low energy negative frequencies were found for the compounds. These frequencies were of ≈0 intensity, but between 68cm-1 and -93cm-1.
When chosing a basis set, computational difficulty and accuracy of the basis functions, i.e. size of the basis set have to be weighed relative to each other. In addition, to simplify the calculations for second row atoms pseudo-potential functions are used that model the core electrons. This also explains why despite using a larger basis set, both optimisation and frequency calculations were very fast. For these compounds the higher level basis LNL2 DZ was used since Cl has 17 electrons and is therefore relatively large on a quantum-mechanical scale.
Calculations for dimer 1 were therefore repeated using different basis sets, however -ve frequencies were still observed: Basis set 3-21G (opt:DOI:10042/to-3339 , freq:DOI:10042/to-3340 ), 6-31G (opt:DOI:10042/to-3341 , freq:DOI:10042/to-3342 ).
However, it was decided that this error does not affect the data of interest in this project. For all dimers the -ve frequency vibration referred to the rotation of the methyl-group, which is difficult to eliminate. Also, the integral was already set to ultrafine. Changes that would be required to fully converge the frequency analysis are beyond the timeframe assigned for this project. In addition, from the .log file output the 2 important MAX and RMS forces were successfully converged. For dimers with -ve frequency only the RMS displacement was not convered.
The same basis set and method were used for all calculations, i.e. for optimisation and frequency or population in the form of molecular orbitals. The reason for this is that for instance frequency or molecular orbital calculations are done on the optimised structure. This optimised molecule was obtained using a particular basis set. The basis set is the functions that describe the electronic structure for a compound and therefore has to be consistent for different calculations based on the same compound. E.g. if a higher level basis set was used for the population than the optimisation, the electronic structure would be different and this would mean that in fact the population under these conditions is for excited electron density.
Results
The following table 2 shows a summary for the optimisation and frequency calculations for each dimer and corresponding DOIs.
| Dimer | Optimisation | Vibrations |
| Dimer 1 | 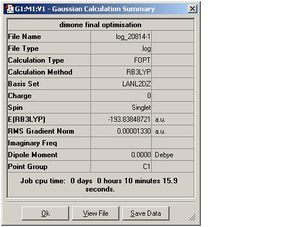 |
DOI:10042/to-3160 |
| Dimer 2 | 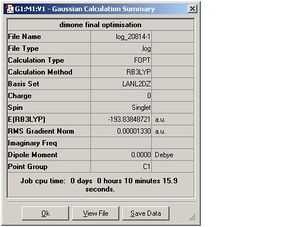 |
DOI:10042/to-3163 |
| Dimer 3 | 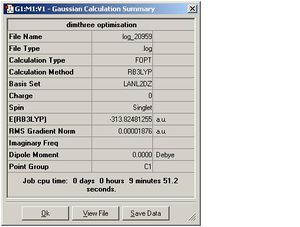 |
DOI:10042/to-3165 |
| Dimer 4 | 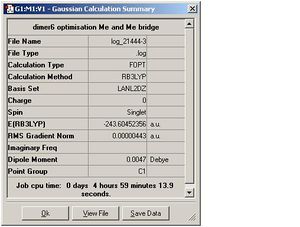 |
DOI:10042/to-3393 |
| Dimer 5 | 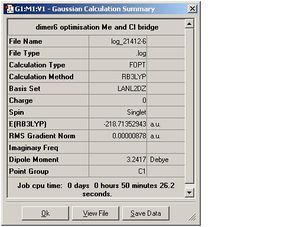 |
DOI:10042/to-3281 |
| Dimer 6 | 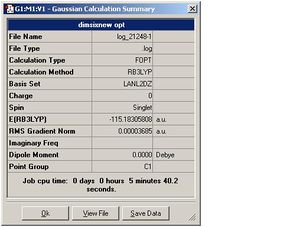 |
DOI:10042/to-3268 |
As can be seen, for each dimers the optimisation and the frequency calculations gave the same energy. The RMS deviation was <0.001. The RootMeanSquare, essentially indicates the deviation of the total energy from the ideal minimum. It is close to 0 and <0.001 for all Dimers computed. This was discussed in detail in part 1 of the Module. Several steps are carried out in the optimisation process until d(total energy) between 2 steps is close to 0 and the minimum energy has been reached. At this stage the RMS value should be <0.001. For each optimisation step the E(R) is computed for that particular position of the atoms. In the initial steps the nuclei and electrons are not in equilibrium and these nuclear-electron interactions within the molecule are not balanced. This imbalance causes a net force which makes the molecule shift to a better position, i.e. the internuclear distance r changes. Since the force is the slope of a energy vs r plot, the molecule will experience a force as long as a change in r causes a change in energy.
The final energy step refers to the equlibrium bond distance at which Nuclear-nuclear repulsion, nuclear-electron attraction and electron-electron interactions are most stabilised, giving the lowest possible energy minima.
For all optimised structures structural bond and energy data was recorded.
For all dimers the distance between Ga and the bridging atom X, the distance between Ga and the terminal group Y, and the Ga-Ga distance was measured. Also, the angle between the 2 terminal groups Y on the Ga was determined.
The results are shown in the following table 3.
| Dimer | Bridging Ga-X distance / Å | Terminal Ga-Y distance / Å | Ga-Ga distance / Å | Terminal Y-Ga-Y bond angle / ° |
| Dimer 1 | 2.51 | 1.96 | 3.70 | 135.2 |
| Dimer 2 | 2.67 | 1.96 | 3.88 | 134.8 |
| Dimer 3 | 2.46 | Ga-Me=1.94, Ga-F=1.73 | 3.59 | 129.7 |
| Dimer 4 | 3.38, 1.99 | 1.98 | 4.09 | 120.2 |
| Dimer 5 | Ga-Cl=2.49, Ga-Me=2.23 | 1.97 | 3.03 | 130.3 |
| Dimer 6 | 2.48 | Ga-H=1.56, Ga-Me=1.96 | 3.65 | 135.2 |
| Dimer | E monomer / a.u. | E dimer / a.u. | ΔE = 2xEmonomer-Edimer / a.u. | ΔE = 2xEmonomer-Edimer / kJ/mol |
| Dimer 1 | -96.901865 | -193.838487 | 0.034757 | 91.254511 |
| Dimer 2 | -95.115720 | -190.257438 | 0.025998 | 68.257754 |
| Dimer 3 | -156.893007 | -313.824812 | 0.038798 | 101.864157 |
| Dimer 4 | -121.801296 | -243.604523 | 1.931x10^-3 | 5.069841 |
| Dimer 5 | -96.901865 and -121.801296 | -218.713529 | 0.010368 | 27.221186 |
| Dimer 6 | -57.572157 | -115.183058 | 0.038744 | 101.722380 |
Analysis
Relative energies
Ga is electrondeficient (similarly to BH3 and BCl3 in part1). It is therefore expected that dimerisation if favourable for GaZ3 compounds in order to relieve this electron-deficiency. The electron density of substituent Z from another monomer is delocalised onto the empty orbital on adjacent electron deficient Ga, and thus stabilising the dimer.
It was expected that when the bridging bond is a halide, it coordinates to the 2nd Ga atom via its readily available lone pair.

Therefore, for Dimers 1,2,3 and 6 dimerisation is expected to be energetically favourable.
For dimer 4 the C of the bridging Me group would have to form 5 bonds, which is not common for C and unfavourable. Therefore, the monomeric conformation would have to be favoured over the dimer-structure.
Dimer 5 was computed to give insight into this trend.
From Table 4 above it was seen that for Dimers with halide-bridging (1,2,3 and 6) the energy of the dimer is significantly lower than 2x the energy of the specific monomer, which confirms that as expected these Ga-atoms are more stable in the dimer conformation since the halide heteroatom readily provides a pair of electrons (available lone pair) for formind an additional bond to the second Ga.
However, when the bridging atom is replaced by a C as in Dimer 4 and 5 the relative stability of the dimer over the monomer is less significant. It can therefore be concluded that in terms of Series 1 heteroatoms such as Cl and Br in dimer 1 and 2 are better at donation of electron-density and stabilising the dimer and Me does not readily exist as a 5-coordinated compound.
This can also be concluded from the optimised structure of Dimer 4. In this structure in fact not 4 equivalent 3c-2e bonds are formed, this will be further explained in the next section.
Based on this poor bridging power of Me, dE is smallest indicating the instability of the dimeric form. It was actually expected that dE is -ve, meaning that the monomeric form is actually more stable.
To see an even more significant and obvious kinetic stabilisation of the monomer , Me would have to be replaced by larger R groups. For GaZ3 compounds where Z=very large R group, e.g. Ph3, these large substituents sterically protect Ga from dimerisation. However calculations for such large groups were expected to take too long for this project.
Nevertheless, dE is very small compared to dimers with halide bridging only. Dimer 5 was created to confirm this trend. For compound 5 monomeric stability is less significant than when both bridging atoms are Me-groups as in Dimer 4, but dE is significantly smaller than e.g. for Dimer 1 and 2.
Also, looking at dE for dimer 1 compared to dimer 2 it was shown that it can be expected that down the halide group, dimerisation becomes less favourable. Down the group the halides become less electronegative and hence less electrondensity is available for bridging stabilisation. Furthermore, Cl and Br form relative stable bonds , making formation of a bridging bond energetically favourable. Down the group the lone pair orbitals of the halide become more diffuse and weaker bonds would be formed.
F was not chosen as the bridging atom since its very high electronegative makes it hold onto its LP, which is therefore less readily donated. Cl is better at bridging than Br, shown by the large dE of Dimer 1, as Cl forms stronger bonds.
As for Series 2 it was found that when Me is replaced with F dimerisation is most favoured and the monomer is in comparision least stabilised. This could be due to the fact that the terminal F is very electronegative, i.e. the electronwithdrawing inductive effect dominates, which makes Ga even more electrondeficient, favouring dimerisation. It could be argued that - similar to the analysis in part 1 for BCl3 and BH3 - the GaClF monomer should be stabilised by pi-donation (see part one). The effect of this however is expected to be reduced due to the energy/size mismatch and thus weak 2p(F)-4p(Ga) pi-overlap. Dimer 6 was also shown to favour dimersation, since H is neutral in terms of electrondonating and electronwithdrawing effects. The terminal Me in dimer 1 are weakly electrondonating, which decreases dE for dimer 1 relative to dimer 6, however this effect is limited since Me is only weakly electrondonating and the relative dE stability is only decreased by 10kJ/mol.
Bonds and angles in optimised Dimer structures
From the data above the presence of 3c-2e bridging bonds in Dimer 1-3,5 and 6 was confirmed since for all compounds the four distances between the 2Ga and the 2 bridging X atoms was identical. Dimer 4 was found not to show this trend. In Dimer 4 there are 2 distances to between the Ga and the bridging C. This indicates that the optimised structure for Dimer 4 deviates from the conventional dimer structure. The shorter distance of the 2 Ga-bridging Me bonds is close to the literature Ga-C distance [1]. The longer distance indicates very weak Ga-C bridging interaction only. This confirms the instability of Ga-Me-Ga bridges and in fact the final optimised structure is an intermediate between the dimer and the monomeric form.
Series 1: Based on the energy calculations above it was expected that Cl is better at bridging than Br. This was confirmed as upon changing Cl with Br (dimer2) the bridging bond length between Ga-X increases, indicating weaker bonds. Essentially this means that less electrondensity is accumulated in the bridging area between Ga-Br, due to weaker interaction. The terminal Ga-Me bond lengths are not significantly affected by changing the bridging units.
Series 2: Changing the terminal substituents had little effect on the bridging Ga-Cl bond length. The terminal Ga-Me distance was also unaffected by the changing the substituents.
Furthermore, the terminal and bridging Ga-Cl bond lengths in Dimer 1 and e.g. 5 can be compared. It can be seen that terminal Ga-Cl bonds are shorter than bridging Ga-Cl bonds. This provides evidence that the bridging bonds are weaker, which agrees with the fact that the briding bonds are 3c-2e bonds and the terminal bonds are 2c-2e bonds, i.e. based on this conventional conception of bonds there is a higher electron density between 2 atomic centers in the terminal "normal" bonds than the bridging bonds. The same trend was observed with terminal and bridging Ga-Me bonds as seen in Dimer5. The values can also be compared to literature: The literature bond length of Ga-Cl in GaCl3 is 2.100Å [2]. From the calculations carried out in this experiment, the bridging bond was longer by ≈0.57Å. The terminal Ga-Cl bond is slighlty longer, but only by 0.14Å. The literature Ga-F bond in GF3 is 1.74Å (cf reference 2), which compares well with the data obtained above. The terminal Ga-H bond length in dimer 6 is nearly identical to the literature terminal Ga-H bond in Ga2H6 of 1.577Å [3] . As are the terminal Ga-Me distances, for which the literature value of Ga-C = 1.968Å was found ([4]. In Dimer 5 the bridging Ga-Me is longer than this literature value, and the terminal Ga-Me agrees with the literature.
Bond angles were also computed to find out more about whether Ga is more sp2 or sp3 hybridised. It was found that the angles between the 2 terminal groups were closer to the trigonal planar angle of 120° than to the ideal tetrahedral angle of 109°. This also indicates that there is significant interaction between the 2 Ga-atoms. The Ga-Ga distance was therefore also measured. The literature value for the Ga-Ga separation in Ga2H6 was found to be 2.69Å (ref3). The Ga-Ga distances found in this experiment are significantly longer. However, in the reference above a different pseudo potential was used. It was difficult to find literature using the exact same calculation settings, hence giving more accurate reference data.
Therefore, to investigate this further the MOs for all dimers, relevant for this interaction were computed and are shown in the next section.
Further bonding analysis using MO and NBO calculations
In the following the MOs computed for dimer 1 were looked at in detail. Subseqeuntly, the HOMO and LUMO for the other dimers were compared. Further information was obtained from the NBO analysis
MOs for Dimer 1
In this part the MOs computed for Dimer 1 were examined DOI:10042/to-3317 . It was focused on the HOMO-LUMO region. Also, as the MOs get higher in energy they become more diffuse and abstract.
| LUMO and above | MO# | LUMO 29 | 30 | 31 | 33 | |||
|---|---|---|---|---|---|---|---|---|
| Computed MO |  |
 |
 |

| ||||
| HOMO and below | MO# | HOMO 28 | 27 | 26 | 25 | 24 | 23 | 21 |
| Computed MO |  |
 |
 |
 |
 |
 |

|
Description:
33 ... bonding in-phase interaction between the 2 Ga-atoms
31 ... antibonding between the 2 Ga-atoms, across the bridging area and also in the terminal Ga-Me region
30 ... antibonding, but significant electrondensity between the 2 Ga-atoms, which indicates that Ga is sp2 hybridised
29 ... LUMO, antibonding out-of-phase overlap across the bridging region
For these MOs it can seen that on goign from 29 to 33 the number of nodes in the MO increases, hence the total enegy increases Also, 29 is assumed to be close to non-bonding as there is no electron density across the terminal Ga-Me bonds. Also, this MO is still slightly -ve in energy, indicating little andti-bonding character. Therefore it can be assumed that the [Ga2Cl2Me4]- is stable and exists since electrons are donated into this low-energy non-bonding LUMO.
28 ... HOMO, many nodes, less diffuse, p-lone pair orbital on Cl, terminal Ga-Me bonding overlap
27 ... no contribution of Cl AOs, bonding orbitals in Ga-Me
26 ... p-orbitals on Cl
25 ... bonding overlap of terminal Ga-Me bonds
24 ... bonding in bridging region only
23 ... bonding interaction across the 2 planes of the molecule, only 1 node
21 ... MO that describes bonding in bridging region only
In addition MO#11 and 12 are thought to be the main bonding contributions with bonding interactions across the bridging region, and delocalisation onto the terminal units.
MO 12 could also be used as confirmation for the sp2 hybridisation of Ga and that the bridging bonds are formed from overlap of the empty p-orbital of Ga with the p-orbitals on Cl. Furthermore in MO12 significant electron density can be found in the space between the 2 Ga-atoms, indicating sp2 hybridisation. This would not be the case if Ga was sp3 hybridised.
 |
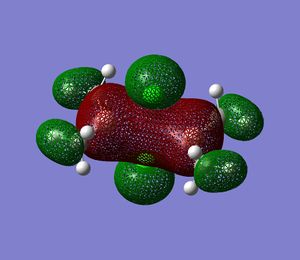 |
Furthermore, MO 30, 31 and 33 show significant bonding electron density between the 2 Ga-atoms.
MOs for other Dimers
For the other dimers, therefore the HOMO and LUMO were studied (left image:HOMO, right image:LUMO).
Dimer 2 DOI:10042/to-3260

|

|
As for Dimer 1 MOs computed showed significant electron-density between the 2 Ga-atoms. e.g. 34 and 31 As expected the HOMO 28 and the LUMO 29 were almost identical for Dimer 1 and 2. All other MOs described for Dimer 1 were found nearly identical in Dimer 2. The MOs describing primarily the terminal units were unchanged. The main difference was found in MO 11, which as for Dimer 1 (MO13) describes bridging bonding interaction. However, it can be seen that there is less electron distribution across the bridge, which is in agreement with the previous analysis that Cl is better at bridging than Br. Furthermore, for Dimer 1 there is another primarily bridging bonding MO 21, which was not found for Dimer2.
For the other dimers the HOMO and LUMO are shown below
Dimer 4 DOI:10042/to-3396
|
Dimer 5 DOI:10042/to-3275
|
Dimer 3 DOI:10042/to-3261
|
Dimer 6 DOI:10042/to-3266
|
Series 1:
Dimer 1,2,5 and 4
The HOMO remains largely unchanged. pi-bonding interaction in the bridging area. Sigma-star type bonding in the terminal region, antibonding on the bond.
However, it can be seen that the pi-bonding interaction in the bridging area is reduced in Dimer 5, which further confirms that Me is weaker as a bridging atom.
The LUMO for Dimer 1 and 2 remains unchanged. From its energy it was also seen that the LUMOs across series 1 are all low-lying in energy and non-bonding rather than anti-bonding.
The LUMO in Dimer 5 shows large diffusion around the Cl.
Series2
Dimer1,3,6
As the substituents are changed, it was found that the HOMO shows the same out-of-phase pattern, but compared to Dimer 1 in Dimer 6 and 3 there are fewer nodes in the terminal region.
The main difference is the LUMO in Dimer 3, which has significant antibonding out-of-phase overlap in the bridging regions and the LUMO is anti-bonding rather than non-bonding.
NBO analysis
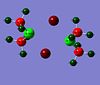
Since the MO computed above are very delocalised and complex, the charges in all dimers are shown below, to get a better understanding of where the areas of high electron density are:
 |
 |
 |
 |
 |
 |
| Dimer | Charge on bridging atoms | Charge on Ga |
|---|---|---|
| 1 | -0.430 | 0.926 |
| 2 | -0.392 | 0.858 |
| 3 | -0.387 | 1.088 |
| 4 | -1.035 (Me-C) | 0.980 |
| 5 | -0.397(Cl) | 0.900 |
| 6 | -0.420 | 0.735 |
These atomic charges were found to give more information of the change to the bridging bonding.
From this it can be seen that significant electrondensity delocalised in the bridging area and that the bridging bonds are most strong for dimer 1 as Cl is most -ve. For dimer 2 the -ve charge on Br is less, indicating weaker bridging.
The fact that the charges for both bridging atoms are the same, confirms that the compound is in fact a dimer and has 4 equal bridging bonds.
Upon comparing the the charge on Dimer 3 to Dimer 1 and electronwithdrawing terminal group minimises electrondensity in the bridging area. Again, the electrondonating effect of terminal Me on the bridging are is not significant as the atomic charge on Cl in Dimer 6 is close to Dimer 1.
In all compounds Ga has +ve atomic charge, which shows that it is Lewis acidic.It is most lewis acidic in compound 3 since the strongly electronwithdrawing F is attached as the terminal group. This agrees with the fact that dimerisation is most favourable for Dimer 3 to relieve this large electrondeficiency. This electrondeficiency is reduced in Dimer 6 and 1.
The NBO analysis also confirms that Ga is sp2 hybridised. This was taken from the log-file for dimer 2.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.94103) BD ( 1)Ga 1 - C 2
( 20.18%) 0.4492*Ga 1 s( 36.79%)p 1.72( 63.21%)
IR analysis for Dimer 1
When analysing the IR data for Dimer 1 it was primarily focused on the stretches relevant for this project, namely vibrations of the Ga-Me and the Ga-Cl bonds. Table 7 shows a summary of these vibrational modes found. Also, when multiple signals in the same region were found, frequencies were selected based on their relative intensities.
Furthermore, as mentioned at the outset, the C-H bonds of the Me attached to the Ga could not be a 100% optimised. Therefore a high number of Me-vibrations were observed. Any vibrations corresponding to these Me-Hs were not included in the analysis.
The frequency analysis is the second derivative of the potential energy surface. If the curvature, i.e. the second derivative is +ve, there is a minimum of the curve. Therefore, the +ve vibrational frequencies obtained confirm that specific compound has been optimised to its ground state. A -ve frequency would indicate a maximum, which would mean that is in an higher energy state and not at the lowest possible point of the PES-curve (shown in part 1), but in fact in a transition state. However, as mentioned at the outset the 2 main forces were converged in this calculation, and the data was used.
This confirmed that only 2 different kinds of bonds are formed in this molecule. the 3c-2e bonds are weaker and require less energy to be stretched. Therefore, the terminal bond stretching frequencies are at a significant higher wavenumber (E=hv' where v'...wavenumber/cm-1).
Also, at 104.39cm-1 and 167.20cm-1 vibrations corresponding to Ga-Ga stretching were observed. Even though these frequencies are very weak, this could be taken as a further confirmation for the sp3 hybridisation of Ga.
In order to get a better insight into the strength of the bridging bonds across the 2 series, the frequencies of the 2 main stretching vibrations of the bridging bonds in all dimers were tabulated below and then compared to Dimer 1.
Based on the relative energies calculated in table 4 it was expected that Dimer 1 and 3 and 6 have highest stretching frequencies as they form most stable bridging bonds, i.e. strongest brigding bonds and hence a higher energy input is required to stretch these bridging bonds.
| Dimer 1 | Dimer 2 | Dimer 3 | Dimer 4 | Dimer 5 | Dimer 6 |
|---|---|---|---|---|---|
| Dimer 1 vib#13 | #18, 178.54, 42 | #15, 259.53, 84 | #22, 562.00, 69 | #17, 267.33, 33 | #10, 232.01, 41 |
| Dimer 1 vib#17 | #16, 161.96, 94 | #14, 251.38, 163 | #13, 152.48, 19 | #16, (Cl) 194.14, 24 | #11, 241.76, 152 |
From the frequency of the Ga-bridgingX stretches it was further confirmed that Cl forms stronger bridging bonds than Br since in Dimer 1 the energy required to vibrate the Ga-Cl bond is significantly higher than in Dimer 2 for the Ga-Br bond.
Also, compared to Dimer 1 in Dimer 5 the Ga-Cl stretch is at a lower frequency indicating that the bridge in Dimer 2 (i.e. Ga-Cl-Ga) is longer. This could be also due to the weaker bridging capability of Me.
The stretching vibrations of the bridging bonds in dimer 4 also confirmed that this compound is closer in monomeric conformation. Significantly higher energy is required to stretch the shorter bond of the 2 distances to the bridging Me-C. Little energy is required to cause stretching of the longer of the 2 bridging distances. This indicates that in contrast to the other compounds, in Dimer 4 "normal" 2c-2e bonds are formed to one of the Ga-atoms rather than 3c-2e bonds. The 2nd bridging "bond" is significantly longer in distance than the other 3c-2e bonds observed and hence requires a low frequency for vibration.
Dimer 3 also confirms what was previously found, namely that the electronwithdrawing terminal F-atom stabilises the Dimer and strengthens the bridging bonds. Compared to Dimer 1 and 6 in Dimer 3 higher energy is required to stretch the bridging Ga-Cl bond.
Conclusion
From this analysis it was found that the heteroatoms with lone pairs form best bridging bonds. In this case of as you go down the halide group these LP coordinating 3c-2e bonds become weaker. Cl was found to form most stable bridging bonds. Furthermore, in Ga2-dimers 2 different types of bonds are formed: 3c-2e bridging bonds and "normal" 2c-2e terminal bonds. The bridging bonds are weaker than the terminal bonds. The stability of the dimer relative to the monomer can be increased by attaching terminal electronwithdrawing groups and hence making the Ga more electrondeficient, however the affect of changing the terminal groups on the bridging bonds was found not to be very significant. Comparing the IR frequencies corresponding to the same Ga-bridgingX stretches and comparison of the dimer energy and the 2xthe monomer energy was found to be most efficient for this analysis. Furthermore, it was found that using this computational method the real structure of the Ga2Me6 dimer could be predicted, which was found to significantly deviate from the conventional conception of GaZ3 dimers and 3c-2e bonds. This is one of the benefits of this computational method, in that the real structure of a compound can be computed.
Mini-Project References
- ↑ Structure of methylbis(salicylaldoximato-O1,N)gallium(III):S. J. Rettig, A. Storr and J. Trotter,Crystal Structure Communications, 1992,48,1587-1590 DOI:10.1107/S0108270192001318
- ↑ Ab Initio Studies of the GaH3−H2O, GaF3−H2O, and GaCl3−H2O Molecular Complexes:Kimberly A. Grencewicz and David W. Ball, J. Phys. Chem., 1996, 100 (14), 5672–5675 DOI:10.1021/jp952885k
- ↑ Ab initio theoretical studies of gallium compounds: Part I. Digallane and gallane:Brian J. Duke, Journal of Molecular Structure: THEOCHEM, 1990,208(3-4), 197-204 DOI:10.1016/0166-1280(90)80006-A
- ↑ An ab initio molecular orbital study of the trimethylgallium-arsine adduct: (CH3)3Ga:AsH3), Charles W. Bock, Structural Chemistry, 1993, 4, 15-18 DOI:10.1007/BF00672094
DOIs for Monomer calculations: GaMeHCl, opt:DOI:10042/to-3325 , freq: DOI:10042/to-3427 GaMe3, DOI:10042/to-3324 , DOI:10042/to-3426 GaMe2Cl, DOI:10042/to-3320 , DOI:10042/to-3321 GaMeFCl, DOI:10042/to-3319 , DOI:10042/to-3428 GaMe2Br, DOI:10042/to-3322 , DOI:10042/to-3323
References for the first part are stated in the other wiki-page














