Rep:Mod2:hulahoops312

Module 2:Inorganic Computational Chemistry Lab

Objectives

The aim of this experiment is to use basis sets within Guassian to calculate the total energies, molecular orbitals, geometrical parameters, IR frequencies and distribution of electronic charge for a range of molecules. In addition to this a mini project is carried out to investigate the favoured stereoisomers within the Schlenk equilibrium for a Grignard reaction.

Boron Molecules

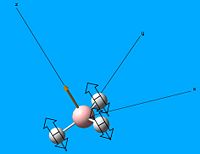
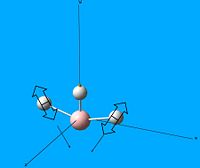
Borane, BH₃

Borane, BH₃ was drawn out on Gaussview 5.0 and was optimised with the calculation method: B3LYP, calculation type: OPT and the basis set: 3-21G. From this the optimised borane structure was produced:

Optimised borane structure

Product 7

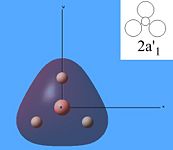
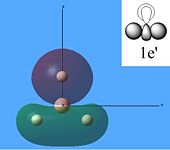
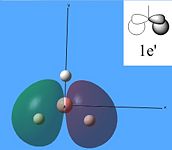
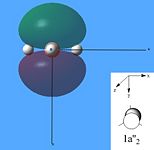
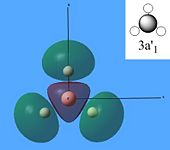
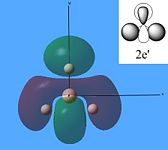
The molecular orbitals were then calculated from the optimised BH₃ molecule on Gaussian and were viewed through Gauss View 5.0, which are shown below.

Molecular Orbitals of BH₃

MO 1 (HOMO-3)

MO 2 (HOMO-2)

MO 3 (HOMO-1)

MO 4 (HOMO)

MO 5 (LUMO)

MO 6 (LUMO+1)

MO 7 (LUMO+2)

MO 8 (LUMO+3)

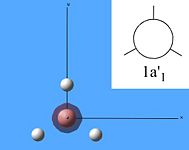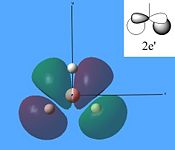From studying the images above it can be seen that there is quite good correlation between the calculated quantitative molecular orbitals and the qualitative LCAO molecular orbitals. This is seen in all the images above apart from MO 8 where they are quite different in appearance and therefore shows that the qualitative approach gives chemists a good idea of the MOs but it still has its limitations.

NBO analysis produced charge distribution for BH₃ where the boron atom has a positive charge of +0.198 Debye and the hydrogen atoms have a negative charge of -0.066 Debye each. This therefore means that the hydrogen atoms possess more electron density to that of the central boron due to it being more electropositive.

Natural Bond Orbital charges for boron and hydrogen

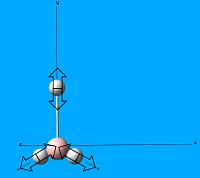
Frequency

This was followed by the vibrational frequencies being calculated from the optimised BH₃ molecule and the summary information of this calculation is shown below in table 1. From this it can be seen that the energy of the optimised borane molecule was -26.46 atomic units (-69.49x10³ KJ mol^-1).

Table 1: Summary information on the optimised BH₃

Filename	DOUGLASHUNT_BH3_freq
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46226338 a.u.
RMS Gradient Norm	0.00020662 a.u.
Imaginary Freq	0
Dipole Moment	0.0000 Debye
Point Group	D3H

IR spectrum for BH₃

There are 6 calcualted frequencies for BH³ and we can tell there are 6 frequencies from the 3n-6 rule for non linear molecules. 3 peaks are shown on the IR spectrum since 2 pairs of vibrational states are degenerate and vibration 4 has an intensity of 0, therefore it does not appear. The vibrations are assigned on the spectrum image on the right.

Table 2: Motions, frequency and intensity of each vibration for trigonal planar BH₃

Vibration No.	Form of the vibration	Frequency (cm-1)	Intensity	Symmetry of D3h point group
1		1145	93	a" 2
2		1204	12	e'
3		1204	12	e'
4		2598	0	a' 1
5		2737	104	e'
6		2737	104	e'

Thallium Tribromide, TlBr₃

Thallium Tribromide was optimised on Guassian and the summary file (shown below in table 3) shows that the calculation method was RB3LYP, the calculation type was FOPT, the basis set was LANL2DZ and the convergence was achieved at -91.22 atomic units (-239.5 KJ mol^-1).

The same method and basis set was used for the frequency calculation so it is comparable to the optimisations calculations.

Frequency analysis is essential within this calculation due to it being the second derivative of the potential energy surface. This means that if all the frequencies are all positive the system is at a minimum, if one of them is negative the optimised system is at a transition state, and if more than one are negative then the calculation has failed to find a critical point, which means the optimisation has failed. This therefore gives us a method of seeing whether the calculation has worked.

Table 3: Summary information on the optimised TlBr₃

Filename	douglashunt_tlbr3_optimisation
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-91.21812851 a.u.
RMS Gradient Norm	0.00000090 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time	days 0 hours 0 minutes 38.0 seconds

By looking at table 4 it can be seen that none of the frequencies are below -5 cm^-1 and so shows that the optimisation has been reached and is at a minimum and not a maximum. Therefore the geometry of TlBr₃ has been successfully optimised.

Table 4: Frequencies of TlBr₃

Low frequencies (cm-1)	-3.42	-0.0026	-0.0004	0.0015	3.9367	3.9367
"Real" normal frequencies (cm-1)	46	46	52	165	211	211

Table 5: Optimised parameters of TlBr₃

Tl-Br bond distance	Br-Tl-Br bond angle
2.65 Å	120.0 o

The literature value for the bond length is 2.41 Å.

Even though the optimised Th-Br bond distance is 0.24 Å longer than the literature length it is of the right magnitude and still very close, which shows that the result is not unreasonable. Gaussview draws bonds based on distance criteria and bonds can “disappear” on Gaussview due to the distance exceeding a set value. However this does mean the bonds are still there but just that Gaussview has not drawn them. The only reason they are even shown is due to them being a structural convenience to us chemists.

In this case a chemical bond is an attraction between atoms which allows the formation of molecules, which contain two or more atoms. A chemical bond is the attraction caused by the electromagnetic force between opposing charges or between nuclei and electrons and the strength of bonds varies significantly. We chemists represent this interaction as a line (or stick) even though it does not physically resemble this however this helps us understand the molecule in a qualitative way.

An organometallic complex: Isomers of Mo(CO)₄L₂

Optimisation

The cis isomer of and the trans isomer of were drawn out on Gaussview and were optimised with the B3LYP method, and the level basis set LANL2MB to get the rough geometry. In addition to this opt=loose was typed into the additional key words section .

After this the cis conformer had one chlorine on one group positioned so the bond was parallel with the top axial Mo-C bond while the other chlorine on the other group was positioned so the bond was parallel with the bottom axial bond. Which is shown in the link and image below.

The trans conformer had both the PCl₃ groups eclipsed to each other with both PCl₃ groups having one chlorine parallel to one M-C bond. Which is shown in the link and image below.

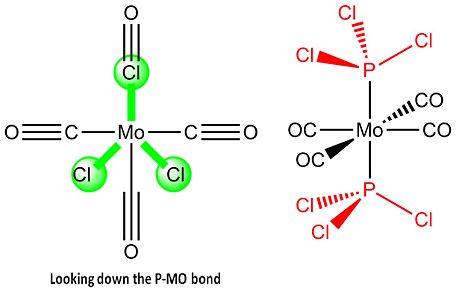
This was followed by the optimisation calculation being carried out again but using the LANL2DZ pseudo-potential and basis sets with "int=ultrafine scf=conver=9" entered within the additional key words section .

Fully optimised cis-Mo(CO)4(PCl3)2	Fully optimised trans-Mo(CO)4(PCl3)2
Fully optimised cis-Mo(CO)(PCl)	Fully optimised trans-Mo(CO)(PCl)

From studying table 6 below it can be deduced that the cis isomer is more stable by 2.73 KJ mol^-1, which is not a very large energy difference when compared to the literature value of 72.98 KJ mol^-1. The reason why my calculated difference is a lot smaller will most likely be due to the literature using the PPh₃ ligands and the steric hindrance will have more of an effect upon the energy since PPh₃ are much bulkier ligands.

The reason why the cis isomer is more stable is most likely due to the the angle between the Mo and the other ligands being distorted to accommodate the PCl₃ ligands and therefore lowering the energy of the complex.

A way to make the trans isomer more stable to that of the cis would be by making the ligand L=PR₃ bulkier by using PPh₃, P^tBu₃ or other bulky ligands. This would lead to large amounts of steric hindrance between the PR₃ ligands on the cis isomer, leading to it destabilising and so making the trans isomer more stable when compared to the cis isomer.

Table 6: Total energies of the cis and trans isomers of Mo(CO)₄(PCl₃)₂

Molecule	Total energy, atomic units	ΔE, atomic units (cis-trans)	ΔE, KJ mol-1 (cis-trans)
cis-Mo(CO)4(PCl3)2	-623.57707196	-1.04086 x 10-3	-2.73
trans-Mo(CO)4(PCl3)2	-623.57603110
Literature
cis-Mo(CO)4(PPh3)2	-1923.05810468	-27.79717 x 10-3	-72.98
trans-Mo(CO)4(PPh3)2	-1923.03030751

The bond lengths and angles below are not exactly the same as the literature values due to them being for the complexes with PPh₃ ligands.

The reason why the angles for P-Mo-P are not exactly 95 ^o (cis) and 180 ^o (trans) for both complexes is due to the electron density on the PCl₃ ligands repelling other ligands electrons and hence distorting the angle. This effect is further emphasised within the literature values by the PPh₃ ligands being larger and therefore distorting the angle more.

Another point to be made is that the equatorial C-Mo bond length is shorter to that of the axial within the cis isomer. The reason for this is due to the CO acting as an electron withdrawing group to the PCl₃ and so gaining electron density. This therefore makes the bond shorter.

Table 7: Geometric parameters of the cis and trans isomers of Mo(CO)₄(PCl₃)₂

cis bonds	length (Å)	cis literature values	trans bonds	length (Å)	trans literature values
axial Mo-C	2.06	2.022 and 2.059	axial Mo-C	2.45	-
equatorial Mo-C	2.01	1.972	equatorial Mo-C	2.45	2.01
P-Mo	2.51	2.58	P-Mo	2.45	2.50
P-Cl	2.24	-	P-Cl	2.24	-
triple bond CO	1.17	-	triple bond CO	1.17	-
cis bonds	angle		trans bonds	angle
P-Mo-P	94.2 o	104.62 o	P-Mo-P	177.4 o	-
Cl-P-Mo-C (dihedral angle)	179.8 o	-	Cl-P-Mo-C (dihedral angle)	174.7 o	-

Frequency

The vibrational frequencies were then calculated with "int=ultrafine scf=conver=9" as additional keywords.

Below in table 8 and 9 are the lowest frequencies for the vibrations of the two isomers. Within the animations below it can be seen that the chlorine atoms are rotating around their phosphorus and the molybdenum centre. This would happen due to the amount of energy required to rotate a bond being very small (in comparison to stretching or bending) and therefore would be taking place at room temperature.

Table 8: Motions, frequency and intensity for the low energy vibrations of cis-Mo(CO)₄(PCl₃)₂

Animation	Annotation	Frequency (cm-1)	Intensity
		11	0
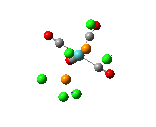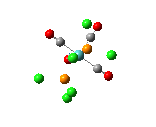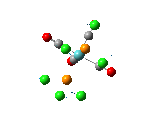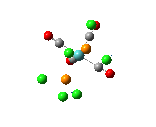		18	0

Table 9: Motions, frequency and intensity for the low energy vibrations of trans-Mo(CO)₄(PCl₃)₂

Animation	Annotation	Frequency (cm-1)	Intensity
		5	0
		6	0

Within the cis isomer there are four distinctive peaks and within the trans isomer there are only three. This is also mentioned within literature and was seen within my second year experiment. The reason why the trans isomer has one less peak is due to it having D_4h symmetry and not C_2v, which leads to the trans isomer having two chemically equivalent stretches (seen in the animations below) at 1950.28 and 1950.91 cm^-1 that are therefore symmetrically degenerate. This gives this one peak a very large intensity compared to the other two peaks.

The other two peaks within the trans isomer are very small in intensity and this is due to the isomer having high symmetry. Therefore the C=O bonds cancel each other out, which is shown in the animations below and so the intensity of these stretches is close to zero.

However within the cis isomer (C_2v point group) the peaks at 1945.31 and 1948.66 are chemically inequivalent C=O bonds that are stretching and therefore they give two distinctive peaks.

The literature and experimental frequencies are also higher to that of the calculated frequencies. One reason for this will be due to basis set over compensating within the calculations and so over estimating the frequencies. Additionally the calculation may not take into account back bonding within the metal complexes between the CO ligands and the metal centre which would weaken the CO bond and so lower the CO frequencies.

Table 10: Motions, frequency and intensity for the carbonyl vibrations of the cis and trans isomers of Mo(CO)₄(PCl₃)₂

cis-Mo(CO)4(PCl3)2
Animation	Annotation	Frequency (cm-1)	Intensity	Literature values (for the PPh3 ligand)(cm-1)	2nd year experimental values (for the PPh3 ligand)(cm-1)
		1945	763	1867	1840
		1948	1498	1896	1870
		1958	633	1924	1896
		2023	598	2026	2024
trans-Mo(CO)4(PCl3)2
Animation	Annotation	Frequency (cm-1)	Intensity	Literature values (for the PPh3 ligand) (cm-1)	2nd year experimental values (for the PPh3 ligand)(cm-1)
		1950	1475	1889	1890
		1951	1467	1889	1890
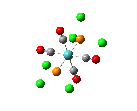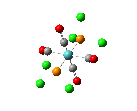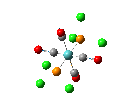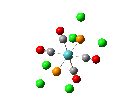		1977	1	1924	1943
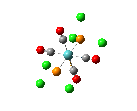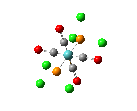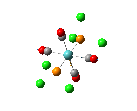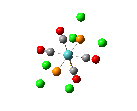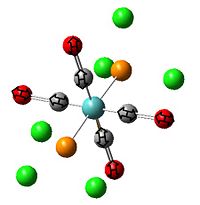		2031	4	2026	2019

IR spectrum for cis-Mo(CO)4(PCl3)2

IR spectrum for trans-Mo(CO)4(PCl3)2

Mini Project

Grignard reagents are alkyl/aryl-magnesium halides which act as nucleophiles by attacking electrophilic carbon atoms that are within polar bonds to create a carbon-carbon bond. They were discovered by Barbier and Grignard in 1900 and were such a significant tool in the formation of carbon-carbon bonds Grignard won a shore of the Nobel prize in 1912.

They are generally solvated by ether, which can lead to halide bridging within solution. A concise description of the situation is given by the Schlenk equilibrium. This is where the solutions of Grignard reagents can contain a variety of chemical species interlinked by equilibria, which is shown below.

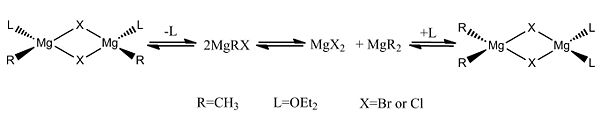
The relative amount of each species present depends upon:

- The size and electronic nature of the R group.

- The size and electronic nature of the halide group, X.

- The nature of the solvent.

- Concentration and temperature.

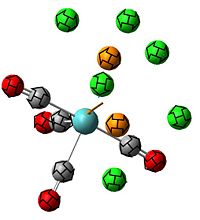
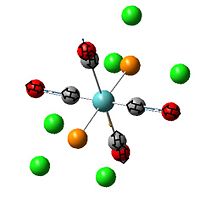
Since the X group changes the ratio of the two isomers within the equilibrium four structures will be drawn out with two being with chlorine bridging atoms (cis and trans) and the other two having bromine as the bridging atoms. From this the thermodynamically favoured isomer can be determined, the IR spectra and bond lengths/angles can be compared and the trans chlorine isomer's molecular orbitals can be analysed.

Therefore the main aim of this mini project is to see whether the bridging halides favour one isomer within the Schlenk equilibrium over another.

Optimisation

The , , and were all drawn on Gaussview 3.0 and were optimised with the B3LYP method, and the basis set 6-311G (d, p).

However the optimisation of the cis bromide isomer and cis chloride isomer failed at the first few steps of the optimisation. This was due to the hydrogen atoms on the diethyl ether being too close (error in the internal coordinate system) and so the Br/Cl-Mg bonds were increased to 3 Å and the diethyl ethers were tilted diagonally so they did not clash. The jmol files of both of these new conformers are below.

Table 11: Total energies of the cis and trans chloride isomers

Molecule	Total energy, atomic units	ΔE, atomic units (cis-trans)	ΔE, KJ mol-1 (cis-trans)
	-1868.21241703	4.4579 x 10-3	11.71
	-1868.21687493

From the table 11 it can be deduced that trans chloride isomer is more stable in terms of it's total energy compared to the cis conformer. This will most likely be due to the steric hindrance between the diethyl ether substituents in the cis conformer which would destabilise it. Therefore the "nature" of the solvent favours the trans conformation.

Table 12: Total energies of the cis and trans bromide isomers

Molecule	Total energy, atomic units	ΔE, atomic units (cis-trans)	ΔE, KJ mol-1 (cis-trans)
	-6096.05182941	6.27241 x 10-3	16.47
	-6096.05810182

By studying table 12 it can be seen that the trans bromide isomer is also more stable by comparing total energies. This again is due to the steric clash between the large diethyl ether substituents and so the "nature" of the solvent overrides any affect of the bridging halide groups. This therefore means that the diethyl ether solvent favours the trans conformation.

The bromide Grignard reagent in both conformations within the Schlenk equilibrium are considerably more stable to the chloride Grignard reagent. This is quantitatively shown by the bromo isomer being 4227.841227 atomic units (11.1 x 10⁶ KJ mol^-1) lower in energy.

Table 13: Geometric parameters of the cis and trans chloride isomers

bonds	cis length (Å)	trans length (Å)	literature values
Mg-Cl	2.46	2.48	2.501
Mg-Me	2.10	2.10	-
Mg-O	2.14	2.14	2.111
	cis angle	trans angle
Cl-Mg-Cl	88.7 o	89.3 o	-
Mg-Cl-Mg	89.9 o	90.4 o	-
Cl-Mg-O	100.1 o	101.7 o	-
Cl-Mg-Me	124.2 o	124.3 o	-

From looking at table 13 it can be stated that the positioning of the L groups and R groups does not change the bond lengths/angles around the bridging halides. The only slight difference is the trans Mg-Cl length being 0.02 Å longer, which is such a small difference it could be down the inaccuracies of the simulation. However from these geometries it can deduced that the optimisation went well by the bond lengths being the right order of magnitude when compared to the literature values.

Table 14: Geometric parameters of the cis and trans bromide isomers

bonds	cis length (Å)	trans length (Å)	literature values
Mg-Br	2.64	2.35	2.6008
Mg-Me	2.11	2.13	-
Mg-O	2.14	2.02	-
	cis angle	trans angle
Br-Mg-Br	91.9 o	97.1 o	-
Mg-Br-Mg	86.9 o	80.7 o	-
Br-Mg-O	102.4 o	112.3 o	-
Br-Mg-Me	123.1 o	114.4 o	-

From examining the parameters in table 14 it can be seen that they differ between the cis and trans bromide isomers. This mainly shown by the cis Mg-Br bond being 0.29 Å longer. This is most likely due to steric hindrance between the diethyl ethers with bridging bromides within such a small amount of space and so the structure distorts. It does this by lengthening the bridging bonds to lower the amount of repulsion within the conformation. This may possibly be the same reason to why the Mg-O bond is longer too in the cis isomer. However there is a possibility that the accuracy of the calculation was very low and so one of the sets of data is wrong but no errors showed up in any of the log files.

Frequency

Again the frequency calculation was carried out with the B3LYP method, and the basis set 6-311G (d, p).

Within both forms of literature the academics did not carry out any IR spectroscopy and mainly used ¹H NMR and X-ray crystallography to analyse their Grignard compounds. However the frequencies were calculated within this mini project and then examined.

The vast majority of the vibrations within the four isomers were from the diethyl ether substituents and the methyl groups. However the ones which we should be interested in are ones which involve any halogen or magnesium bond vibrating with a significant intensity. In table 15 and 16 below only one of these vibrations were found in which the magnesium atoms were moving without a low intensity. Within both trans isomers the same stretch had higher intensities to that of the cis. This could be due to the two methyl groups on either side of the trans isomers constructively adding to the vibration of the magnesium atoms.

Table 15: Motions, frequency and intensity for the vibrations of the cis and trans chloride isomers

Isomer	Animation	Frequency (cm-1)	Intensity
trans		541	130
cis		539	96

Table 16: Motions, frequency and intensity for the vibrations of the cis and trans bromide isomers

Isomer	Animation	Frequency (cm-1)	Intensity
trans		535	125
cis		533	80

The low frequencies were also checked to see whether all four molecules optimised successfully. Ideally we would want the lowest frequency to be no less than -5 cm^-1, however since there are a large number of hydrogens on the molecules this will be hard to achieve. The reason for this is that the hydrogens require a low level of energy to rotate and so you obtain such low frequencies.

Even though 3 of the 4 low frequencies are less than -5 cm^-1 they are significantly smaller negative numbers that what were originally calculated in the first attempt of the optimisation of both cis isomers.

Table 17: Low frequencies for all four isomers

Isomer	Low frequency (cm-1) :	1	2	3	4	5	6
trans chloro		-1.1083	-0.0012	-0.0011	-0.0011	6.5409	8.6270
cis chloro		-12.9612	-0.0028	-0.0027	-0.0023	2.3104	7.5693
trans bromo		-13.5727	-5.5025	-0.0043	-0.0032	0.0050	5.0600
cis bromo		-6.6564	-0.0081	-0.0081	-0.0068	4.4325	5.8360

Molecular Orbitals and Natural Bond Orbitals

The molecular orbitals were calculated by setting the job type as energy with the B3LYP method, and the basis set 6-311G (d, p). In addition to this the "Full NBO" option was chosen under the NBO tab and "pop=full" was added as additional key words.

From studying the table below it can be seen that after molecular orbital number 38 the interactions become much more anti boning to that of bonding by there being more nodes within the molecule. This would destabilise the entire molecule since these orbitals are occupied and so explains why this molecule only exists temporarily in equilibrium while in solution. The orbitals on diethyl ether substituents within the cis chloride isomer could interact across the halide bridging and further destabilise the molecule by having more anti-boning interactions. Another feature of the molecular orbitals is that the R and L groups do not interact with the magnesium or halide bridging until the higher valence electrons.

Table 18: Molecular Orbitals of the trans chloride isomer

Molecular orbital number	Energy	Images	Description
1 to 4	-101.50454 to -46.76677		No molecular orbitals are being shown
5 to 16	-19.17335 to -10.08695		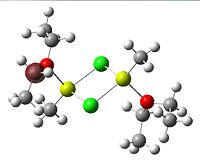Oxygen (molecular orbital numbers 5-6) and carbon S orbitals
17 to 18	-9.41979 to -9.41758		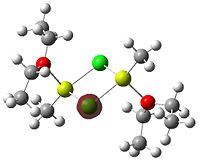S orbitals of chlorine
19 to 24	-7.17860 to -7.17458		P orbitals of chlorine
25 to 26	-3.07208 to -3.07102		S orbitals of magnesium
27 to 32	-1.81923 to -1.81376		P orbitals of magnesium
33 to 34	-1.06952 to -1.06947		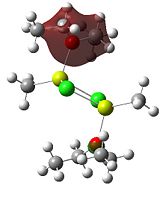S Orbitals have merged on the diethyl ethers
35 to 36	-0.80315 to -0.79860		Anti bonding on opposite ends the diethyl ether substituents by the S orbitals merging
37 to 38	-0.78004 to -0.76977		Bonding interaction (37) and anti bonding (38) interaction between chlorine atoms
39 to 62	-0.75981 to -0.38839		Anti bonding orbitals on the diethyl ether substituents between the hydrogen S orbitals
63 to 78	-0.38038 to -0.29564		A mixture of bonding and anti bonding interactions between diethyl ether, the methyl groups and the chlorine atoms. This is the first evidence that the R and L groups are now bonding with the bridging halides.
79 (HOMO-1)	-0.21924		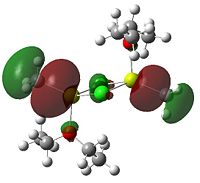Anti bonding between methyl groups and magnesium, which is the first bonding interaction between the R/L groups and magnesium. Chlorine atoms are non-bonding
80 (HOMO)	-0.21276		Anti bonding between methyl groups and magnesium atoms with chlorine this time having more of an anti bonding role. If any electrophile were to attack it would most likely do so at the Mg-Me bond since it has the highest amount of electron density within the HOMO.
81 (LUMO)	+0.00617		Anti bonding between the magnesium atoms with the diethyl ethers, methyl groups and chlorine atoms. Here the electrons are far more delocalised than any of the previous molecular orbitals.

Natural Bond Orbitals for the trans chlorine isomer

NBO from view 1

NBO from view 2

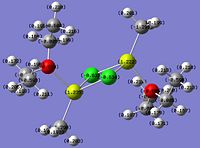By examining the images above it can be distinguished that the chlorine bridging atoms and the oxygen atoms have a large amount of electron density. This will be of course due to them being more electronegative to the hydrogen, carbon and magnesium atoms. In fact they get the vast majority of their electron density from the electropositive magnesium and therefore there will be a considerable amount of ionic character within the bonds.

Conclusion

I conclude that the type of halide bridging does not favour one isomer within the Schlenk equilibrium with the L group (diethyl ether) and R group (methyl group) I picked. This is due to the solvent being too bulky and therefore favours the trans conformer due to steric factors and so the size and electronic structure of the halide bridging it not a decisive factor. From my optimisation total energies I can also conclude that the bromide Grignard reagent is more stable to the chloride one. The energy difference is quite a large value and again is most likely to do with the bromine atoms being bigger and so the L group are further apart so there is no clash in electron orbitals.

From this I also learnt that the vibrational analysis did not tell me a lot about the electronics of the molecule and so understood why in the literature they did not run IR upon their Grignard reagents but carried out x-ray crystallography to determine the structure of the reagents.