Module 2

Optimisation of BH₃

The graphical interface GaussView can be used to create and manipulate molecules, which visually represent the results of calculations carried out by the program Gaussian. A molecule of BH₃ was created using such a program and was optimised with a modified B-H bond length of 1.5A and a bond angle of 120^oDOI:10042/to-3757 .

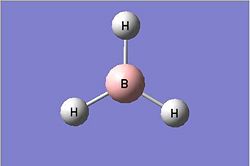
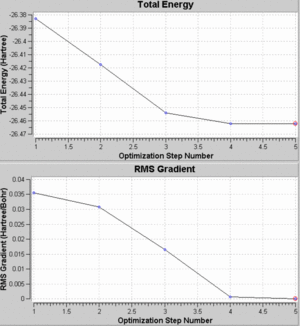
The full summary of the optimisation can be seen below. The optimised B-H bond length can be seen to be 1.193A, whilst the H-B-H angle was 120^o.

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: LANL2MB
Charge: 0
Spin: Singlet
E(RB3LYP): -26.46 a.u.
RMS Gradient Norm: <0.0001 a.u.
Dipole Moment: 0.0000 Debye
Point Group: D₃H
Time Taken: 32 seconds

As BH₃ is a relatively small molecule (consisting of one boron and three hydrogen atoms), the calculation could be processed in a short amount of time and this can be seen from the energy graphs for this optimisation. As the graph shows, there were only five steps required for this molecule to reach an optimised geometry. The energy decreases with increasing steps used until a minimum is reached. This is the point at which the molecule has the optimised geometry.

The MOs for BH₃ were then obtained by using gaussian to calculate a frequency job which can be seen here {{DOI|. Below are the visualisations for the first five molecular orbitals, including the HOMO and LUMO

These visual representations of the MOs can be seen to be in good correlation with MO theory. Below is the MO diagram for BH₃, built from its fragment orbitals of H₃ and Boron.

There are no significant differences between the real and LCAO MOs. The geometries of the bonding MOs from the diagram are very similar to those which have been visually represented and tells us that qualitative MO theory is reasonably accurate and useful for describing the MO theory of BH₃.

**Vibrational Modes of BH₃**
Frequency /cm^-1	Intensity /arbitrary units	Symmetry Label
1144.15	92.87	A₂''
1203.64	12.31	E'
1203.64	12.32	E'
2598.42	0	A₁'
2737.44	103.74	E'
2737.44	103.8373	E'

We can see that two of the vibrations have approximately equal intensities due to them being degenerate, whilst one vibration produces an intensity of zero. This is due to the vibrations producing no change in dipole. Therefore,, we would expect to only see three peaks in the IR spectrum and this can be seen.

Analysis of BCl₃

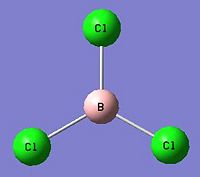
The same method was used to analyse and optimise a molecule of BCl₃ and we can see the summary of the calculation below.

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: LANL2MB
Charge: 0
Spin: Singlet
E(RB3LYP): -69.44 a.u.
RMS Gradient Norm: 0.0001 a.u.
Dipole Moment: 0.0000 Debye
Point Group: D₃H
Time Taken: 7 seconds

The point group of this molecule remains as D_3h, with a bond length of 1.87A and a dihedral angle of 120^o. In comparison with the literature^[1] the bond angle is slightly lower, being 1.72A. However, they do have similar geometries, both being trigonal planar.

The molecular vibrations were then calculated and are represented in the table below.

**Vibrational Modes of BH₃**
Frequency /cm^-1	Intensity /arbitrary units	Symmetry Label
214.13	3.93	E'
214.13	3.93	E'
376.94	43.78	A₂''
417.38	0	A₁'
939.47	258.39	E'
939.47	258.69	E'

In some structures, GaussView does not provide the expected bonds for molecules due to specifically being concerned with the nuclei of the molecules. The bonds between each atom only provide a means to constrain each atom in order for Gaussian to calculate the minimum distance between each of the nuclei.

A bond is an interaction between atoms or molecules and is associated with the sharing of electrons from each atom's atomic orbital, to form molecular orbitals . The strength of the bond depends significantly on the overlap of these atomic orbitals forming the bonding molecular orbitals. The number of electrons and nuclei which contribute to this bond will vary depending on the different atoms in each case.

Isomers of Mo(CO)₄L₂

Introduction

The stability of both cis and trans isomers for this molecule may be obtained by applying the same methods used in the previous exercises. Fully optimising the structure allows valuable information on the stability of each isomer to be obtained and may lead to an understanding as to which one is the most energetically favourable. The molecule used in this calculation is Mo(CO)₄L₂, where the L ligands should be PPh₃ groups. However, these ligands would be too big for Gaussian to calculate the optimised energies in a short amount of time. Therefore, chlorine atoms are substituted for the phenyl groups on the phosphorous and the energies of the cis and trans isomers of Mo(CO)₄(PCl₃)₂ can be calculated with relative ease.

Optimisation and Frequency Calculations

The summary of the optimisation for the cis form of the metallic complex can be seen here DOI:10042/to-3842 .

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: LANL2MB
Charge: 0
Spin: Singlet
E(RB3LYP): -617.53 a.u.
RMS Gradient Norm: <0.0001 a.u.
Dipole Moment: 8.63 Debye
Point Group: C₂V
Time Taken: 14 minutes 28 seconds

This calculation was then repeated using an improved basis set.

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: LANL2DZ
Charge: 0
Spin: Singlet
E(RB3LYP): -623.577 a.u.
RMS Gradient Norm: <0.0001 a.u.
Dipole Moment: 1.304 Debye
Point Group: C₂V
Time Taken: 22 minutes 19 seconds

The summary of the optimisation for the trans form can be seen here DOI:10042/to-3843

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: LANL2MB
Charge: 0
Spin: Singlet
E(RB3LYP): -617.52 a.u.
RMS Gradient Norm: <0.0001 a.u.
Dipole Moment: 0.00 Debye
Point Group: D₄H
Time Taken: 8 minutes 27 seconds

This calculation was then repeated using an improved basis set, similar to the improved set used for the cis isomer.

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: LANL2MB
Charge: 0
Spin: Singlet
E(RB3LYP): -623.576 a.u.
RMS Gradient Norm: <0.0001 a.u.
Dipole Moment: 0.0002 Debye
Point Group: D₄H
Time Taken: 11 minutes 25 seconds

From looking at the summaries for both the cis and trans form of Mo(CO)₄(PCl₃)₂, the isomer that is the most stable would be the cis isomer. According to the energy outputs for optimisation, the calculated energy difference between the cis and trans form is 3kJmol^-1. This is quite a small energy difference and means the cis isomer is 3kJmol^-1 more stable relative to that of the trans isomer. In theory however, trans-Mo(CO)₄(PCl₃)₂ should be energetically more stable and hence more readily formed. This is what was reported in the literature^[2] and can be thought to be due to the steric interactions between the PR₃ ligands being minimised in the trans structure, as the groups are further apart. The difference in experimental energy stabilities could be due to the fact that the Ph groups in the PPh₃ ligand were replaced with a Cl atom, in order to ease the calculations.

The vibrational modes for both the cis and trans isomer were then computed and can be found here DOI:10042/to-4055 and DOI:10042/to-4056 .

**Vibrational Modes of cis-Mo(CO)₄(PCl₃)₂**
Visual Representation	Frequency /cm^-1	Intensity /arbitrary units
	10.43	0.0266
	16.59	0.0079
	1945.48	766.49
	1948.65	1495.75
	1958.49	630.89
	2023.36	599.62

**Vibrational Modes of trans-Mo(CO)₄(PCl₃)₂**
Visual Representation	Frequency /cm^-1	Intensity /arbitrary units
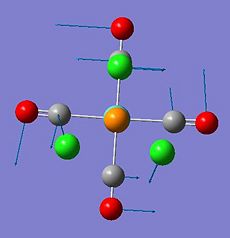	5.29	0.0941
	6.31	0.00
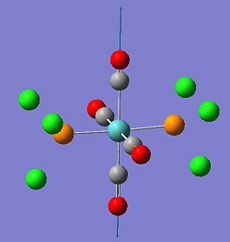	1950.22	1475.23
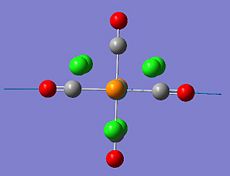	1950.22	1466.86
	1977.13	0.70
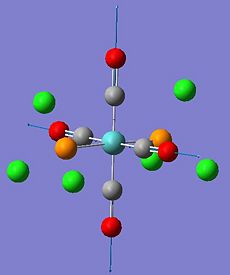	2030.91	3.86

The vibrational modes plotted in the table above are mostly due to the carbonyl vibrations, with the first two being the ones at the lowest frequency. It can be seen that the strongest vibrational modes are the ones which give rise to an overall change in dipole. The higher intensity stretches will involve the movement of the carbonyl groups. This is indeed what is observed looking at the tables of data above. The very low frequency vibrations can be related to the rotation of the P-Mo bonds.

The IR spectra for both the cis and trans isomers is shown below. Looking at the spectrum for the cis isomer, it can be seen that there are four peaks (1945, 1948, 1958, 2023cm^-1 each corresponding to different vibrational modes, whilst for the trans isomer there appears to be three (1950, 1977, 2030cm^-1) due to the symmetry of the trans-isomer. However, this is not the case when comparing the results from the literature ^[3], which reports there to be three vibrational modes for the cis form and only one for the trans form. This is because the geometry of both isomers are not constrained to their point groups, as the calculation is not very accurate. Hence, if the calculation was improved, we would expect to have the precise number of stretches which will be in good accordance with the literature.

Mini Project:Ammonia-Borane for future Hydrogen storage

Introduction

Hydrogen is an important energy source as it reacts with oxygen to release energy with the only by-product being water. However, at atmospheric pressure it is gaseous, and therefore needs to be stored at high pressure to reduce the storage volume. By using a solid material with a high hydrogen content, the volume required for hydrogen storage is considerably reduced, and the need for high pressure eliminated. Ammonia borane is one such molecule which contains a high hydrogen content and is stable at room temperature and can be formed directly from a mixture of NH₄Cl and LiBH₄ in diethyl ether when a trace of NH₃ is present.

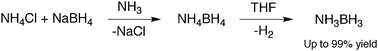
Geometry Optimisation

Ammonia-borane is a relatively small molecule, consisting of three hydrogen atoms per nitrogen and boron element. As such, we can use a relatively high level basis set for the optimisation as the calculations will not take as long compared to that of larger molecules. This was chosen to be B3LYP and 6-31G (d,p). Ammonia-borane exists as both the staggered and eclipsed conformations, similar to that of ethene. The summary of the initial optimisation for both the staggered and eclipsed conformations can be seen below. DOI:10042/to-4161

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: 6-31G (d,p)
Charge: 0
Spin: Singlet
E(RB3LYP): -83.22 a.u
RMS Gradient Norm: <0.0001 a.u.
Dipole Moment: 5.56 Debye
Point Group: C1
Time Taken: 2 minutes 27 seconds

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: 6-31G (d,p)
Charge: 0
Spin: Singlet
E(RB3LYP): -83.21 a.u
RMS Gradient Norm: <0.0001 a.u.
Dipole Moment: 5.61 Debye
Point Group: C1
Time Taken: 1 minutes 57 seconds

It can be seen that the staggered structure is the lowest in energy being slightly more stable than the eclipsed conformer by approximately 8kJmol^-1. This may be accounted for by the minimal steric hindrance between each hydrogen atom granted by this conformation. The post-optimisation B-N bond lengths were 1.688Å and 1.697Å for the staggered and eclipsed conformations respectively, whilst the average B-H and N-H bond lengths in both conformations were very similar, both being 1.20A and 1.02A. The dihedral angle for H-B-H was found to be 113.88^o, whilst the angle for H-N-H was 107.87^o. This is in agreement with the literature values ^[4]

The optimisations for both the staggered and eclipsed structures for ethane were then computed, in order to make a valid comparison with the data gathered for ammonia-borane. For the staggered conformation, the C-C and C-H bond lengths were 1.53A and 1.094A respectively. This is similar in the eclipsed structure, giving 1.54A for the C-C bond and 1.094A for the C-H bond length. The H-C-H bond angles for both were found as 109^o and 107^o. Upon initial comparison bewtween the bond lengths of the B-N bond and C-C bond, we can see a significant decrease in bond length going from ammonia-borane to ethane. This can be considered to be due to the difference in electronegativities of Boron and Nitrogen resulting in more electron density being centred around the nitrogen atom (as it has a higher electronegativity), creating a charge inbalance and hence a polar bond. The NBO analysis aswell as the frequency analysis of the B-N bond will give significant information to the type of bonding involved and looking at the specific molecular orbitals, will help explain the bonding.

NBO Charge Distribution Analysis

The NBO analysis can be found here File:AMMONIA BORANE ECLIPSED NBO.LOG for ammonia borane and was computed and shown here. The extract below was taken from this file, and is key to determining the nature of teh B-N bond.

(1.99414) BD ( 1) N   1 - B   5  
                ( 82.27%)   0.9071* N   1 s( 34.52%)p 1.90( 65.48%)d 0.00(  0.00%)
                                           -0.0001 -0.5873 -0.0166 -0.0002  0.8080
                                           -0.0440  0.0000  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.0027 -0.0016
                ( 17.73%)   0.4210* B   5 s( 15.20%)p 5.56( 84.55%)d 0.02(  0.24%)
                                            0.0000 -0.3894  0.0202 -0.0004 -0.9193
                                           -0.0216  0.0000  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000 -0.0427  0.0247

Looking at this information, it can be seen that 82.27% of the electron density is located on the Nitrogen atom, whilst the remaining 17.73% remains at the Boron. This supports the theory of a polarised B-N bond, due to the differing electron densities of the two atoms. It also shows that the nitrogen atom is sp² hybridised, whilst the boron exhibits the majority of the electron density in its p-orbitals (84.55% compared to 15.20% in s orbitals and 0.24% in d-orbitals). This suggests that the nitrogen atom may be donating electron density to the vacant, low lying p-orbitals of the boron indicating a dative bond between them. In order to investigate this further would be to analyse the molecular orbitals of ammonia-borane and see the visual representation of the electron clouds.

MO Analysis

The frequency calculation can be found here File:AMMONIA BORANE FREQ.LOG and the MOs for Ammonia-Borane up to the LUMO are represented below.

From analysing these representations, the MO of interest is number 3 as this shows the bonding between the boron and nitrogen. The electron density around nitrogen is slightly enveloping around the boron and this signifies a dative covalent bond. The orbitals for Nitrogen are larger and more diffuse than boron and this can be seen from the size of the orbitals in the diagrams.

References

↑ Branchadell, V.; Oliva, A.; J. Chem. Am. Soc., 1991, 113, 4132-4136, DOI:10.1021/ja00011a011
↑ Cotton, F. A.; Darensbourg, D. J.; Klein, S.; Kolthammer, B. W. S. Inorg. Chem., 1982, 21, 294-299 DOI:10.1021/ic00131a055
↑ Cotton, F. A.; Kraihanzel. C. S., J. Am. Chem. Soc., 1962, 84, 4432
↑ T. F.; Siegbahn, P. E. M.; Richardson, T. B.; Crabtree, R. H. Study of the N-H...H-B Dihydrogen Bond Including the Crystal Structure of BH3NH3 by Neutron Diffraction, Journal of the American Chemical Society, 1999, 121, 6337-6343

[1] Branchadell, V.; Oliva, A.; J. Chem. Am. Soc., 1991, 113, 4132-4136, DOI:10.1021/ja00011a011

[cis-2] Cotton, F. A.; Darensbourg, D. J.; Klein, S.; Kolthammer, B. W. S. Inorg. Chem., 1982, 21, 294-299 DOI:10.1021/ic00131a055

[3] Cotton, F. A.; Kraihanzel. C. S., J. Am. Chem. Soc., 1962, 84, 4432

[4] T. F.; Siegbahn, P. E. M.; Richardson, T. B.; Crabtree, R. H. Study of the N-H...H-B Dihydrogen Bond Including the Crystal Structure of BH3NH3 by Neutron Diffraction, Journal of the American Chemical Society, 1999, 121, 6337-6343

[1]

[2]

[3]

[4]

Module 2

Optimisation of BH3

Analysis of BCl3

Isomers of Mo(CO)4L2

Introduction

Optimisation and Frequency Calculations

Mini Project:Ammonia-Borane for future Hydrogen storage

Introduction

Geometry Optimisation

NBO Charge Distribution Analysis

MO Analysis

References

Optimisation of BH₃

Analysis of BCl₃

Isomers of Mo(CO)₄L₂