Rep:Mod2:david90

Module 2

David Freeman

BH3 Optimisation

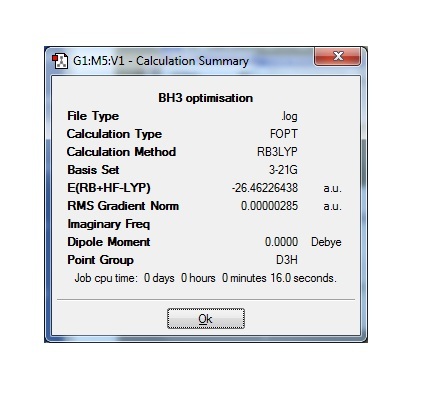
BH₃ was optimised as described in the instructions using a DFT-B3LYP method with a 3-21G basis set. This is a relatively simple basis set so will not give very high accuracy but is good for an initial optimisation. Calculation methods are good for this molecule in particular due to difficulties in isolating it. BH₃ is an important intermediate in many reactions but left on it's own it will dimerise to B₂H₆, making obtaining the physical data of BH₃ problematic. For this reason a computational method of accurately estimating this data is apt. The calculated bond distances and angles are given below.

B-H bond distance:1.19Å

H-B-H angle:120.0^o

The literature value for the B-H bond length is 1.19001(1)Å which is clearly in very good agreement with the calculated value. The sp² hybridized boron is expected to have bond angles of 120^o which also agrees with the calculation. This shows for this molecule the minimal basis set is a good approximation.

To see if the conformation was really minimised the gradient of the total energy vs calculation step was found at the point that the calculation stopped. To do this the summery file of the calculation was found and is shown below.

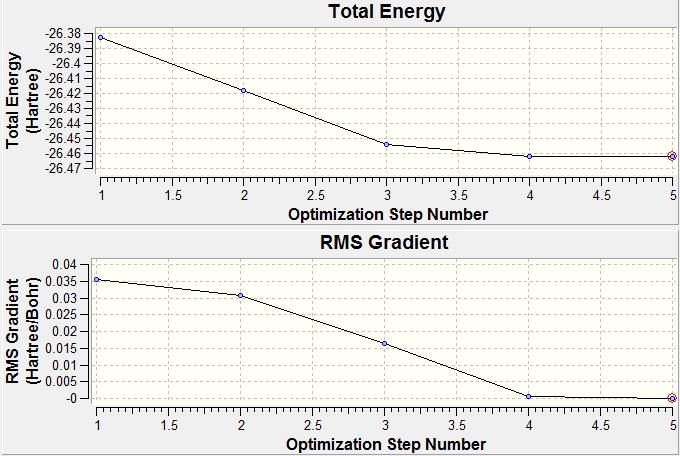
The gradient is very close to 0 which indicates that the calculation has levelled out to a minimum. Each time a molecule was minimized it was checked in the same way by looking at the summery and ensuring the gradient was close to 0. For BH₃ the graphs of total energy vs optimisation steps and root mean square forces vs optimisation steps are shown. Notice that with each step of the calculation the energy gets closer to the final value and finally levels out. The root mean square forces vs optimisation steps graph shows how the gradient of the other graph changes with each step and shows that each time a new step is started the gradient gets closer to 0. This means each subsequent step in the calculation will be closer to the real energy than the last.

http://hdl.handle.net/10042/to-5269 
     This is the optimisation file for BH3

TlBr₃ optimisation

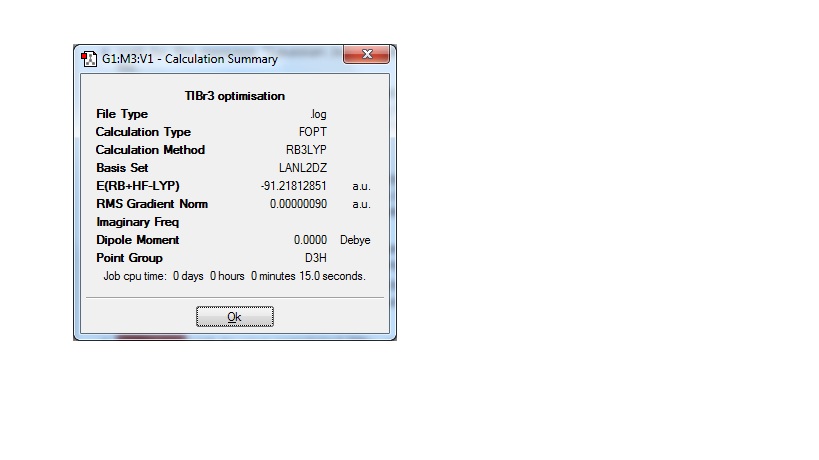
The same method was used on TlBr₃ but the basis set was changed to LANL2DZ which is a more accurate basis set and will better model the heavy thallium and to a lesser extent the bromides. The symmetry was also restricted to D_3h and the tolerance made very tight. The bond distances and angles in this case were:

TlBr3 bond distance: 2.65Å

Br-Tl-Br angle: 120.0^o

http://hdl.handle.net/10042/to-5425

The literature Tl-Br bond distance is 2.52Å. This is in good agreement with the calculation, which has slightly overestimated the distance in this case. One way of getting better accuracy would be to use a more sophisticated basis set that could better model the bonds. The orbitals, especially the valence orbitals, will be more diffuse and less easy to calculate so the basis set will have to be changed to get a better picture of the real molecule.

A frequency analysis was then carried out on the molecule to ensure it had been correctly optimised. The low frequencies that correspond to the vibrations of the centre of mass of the molecule were found to be -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 which are an order of magnitude lower than the lowest real normal mode which was 46.4289. This shows the calculation was indeed accurate and the optimisation was good.

Sometimes Gaussview may not draw in bonds after an optimisation has taken place, this did not occur here but did later in the report in the "Cis and Trans Isomerism of Octahedral Mo Complexes" section where the reasons for this are explained in more detail.

Molecular Orbitals of BH₃

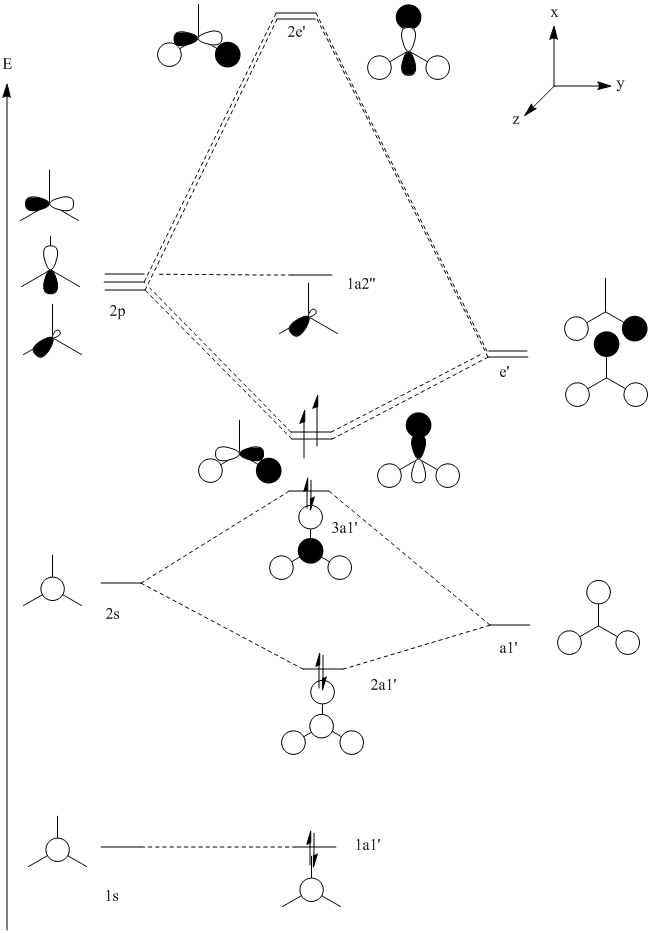
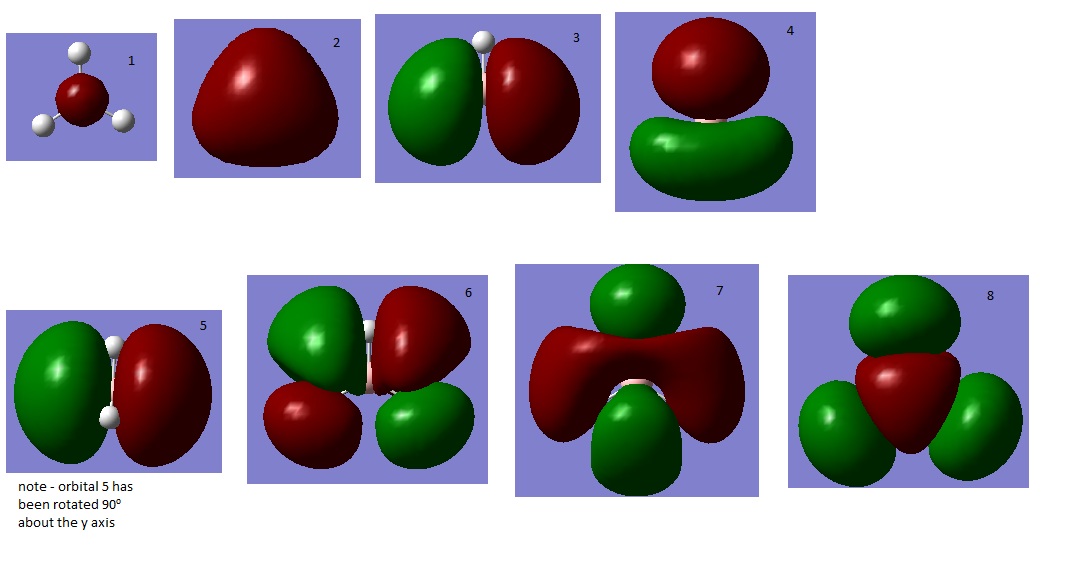
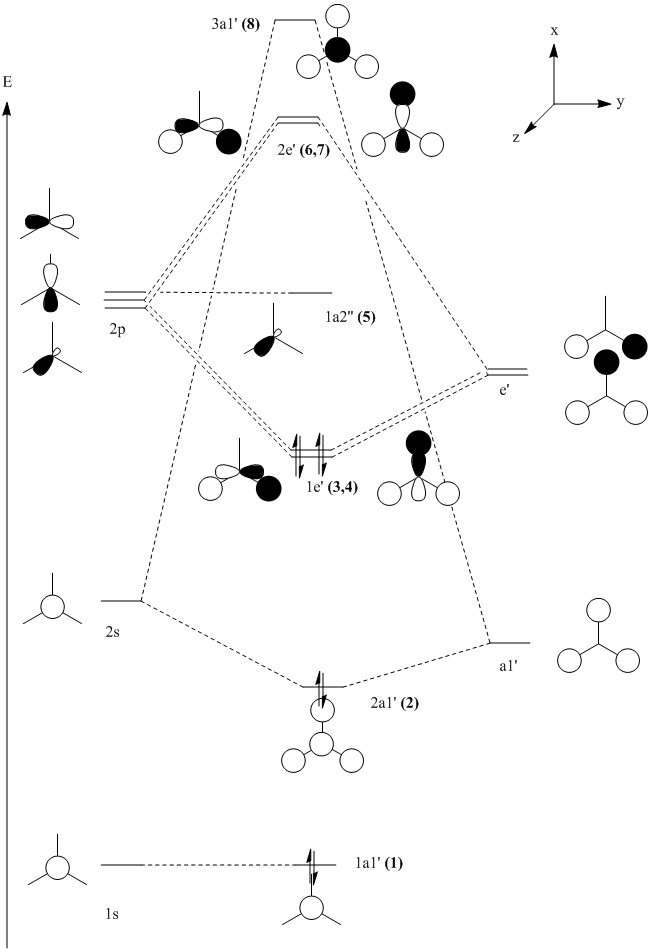
The molecular orbitals of the BH3 molecule were computed. An MO diagram of the molecule has been drawn so that the orbitals may be assigned. Only orbitals 1-8 have been included, after this point the energies of the orbitals increase by a lot, this is due to all the low lying orbitals having been used up and a different shell of orbitals being combined (the 3rd shell for boron and the 2nd for the hydrogens). These orbitals are not very interesting as it is unlikely that any real chemistry will happen in these orbitals.

An MO diagram was drawn using the techniques from second year and is shown below.

By looking at the calculated MOs it is possible to assign each calculated MO to a MO on the diagram and re-draw it to assign energies to each orbital. Pictures of orbitals 1-8 are shown below with the re-drawn MO diagram. The HOMOs are orbitals 3 and 4 (they are degenerate) and the LUMO is orbital 5.

Table of energies for orbitals 1-8

Orbital	Energy
8	0.19192
7	0.18859
6	0.18859
5	-0.07458
4	-0.35681
3	-0.35681
2	-0.51765
1	-6.73049

What is interesting here is how high up in energy the 3a1' (8) orbital is. In the initial diagram this orbital is filled (as the 2s orbital combinations were kept separate to the 2p combinations) yet in the real calculated molecule this orbital is not filled. The LUMO is the pz orbital of the boron. This is unsurprising as BH3 is vulnerable to nuclephillic attack due to it's empty p orbital and electron deficiency, it makes sense therefore that the LUMO is a p orbital. The redrawn diagram also shows that BH3 has no unpaired electrons which shows that it must be diamagnetic.

This shows one of the limitations of MO theory, namely that it is difficult to predict exactly what order the orbitals are in energy and therefore which orbitals will be filled first. Computational methods allow energies to be found for these orbitals which gives a much better idea about which orbitals will be filled in a molecule.

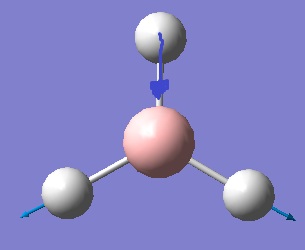
NBO Analysis

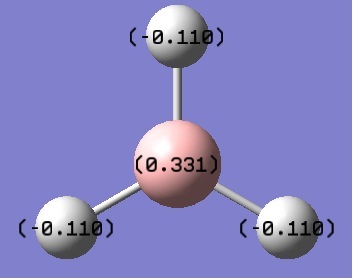
The natural bond order analysis shows how charge is spread across the borane molecule in Debyes. The diagram above shows the atomic charges. It can be seen that most of the charge is on the hydrogens an that the boron is δ⁺, meaning the electron density is mainly on the hydrogens. This makes sense as the boron in borane is very electron deficient and acts as an electrophile.

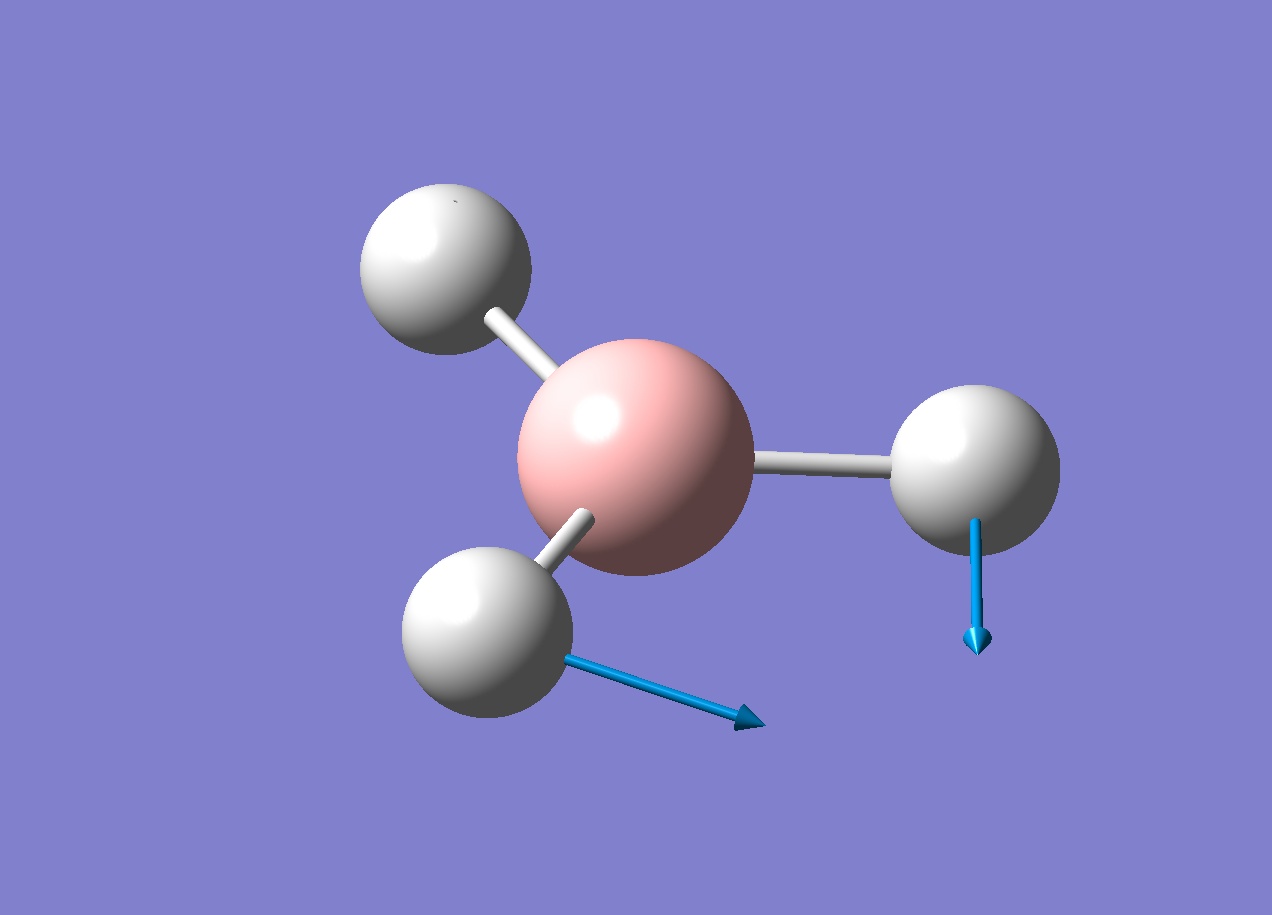
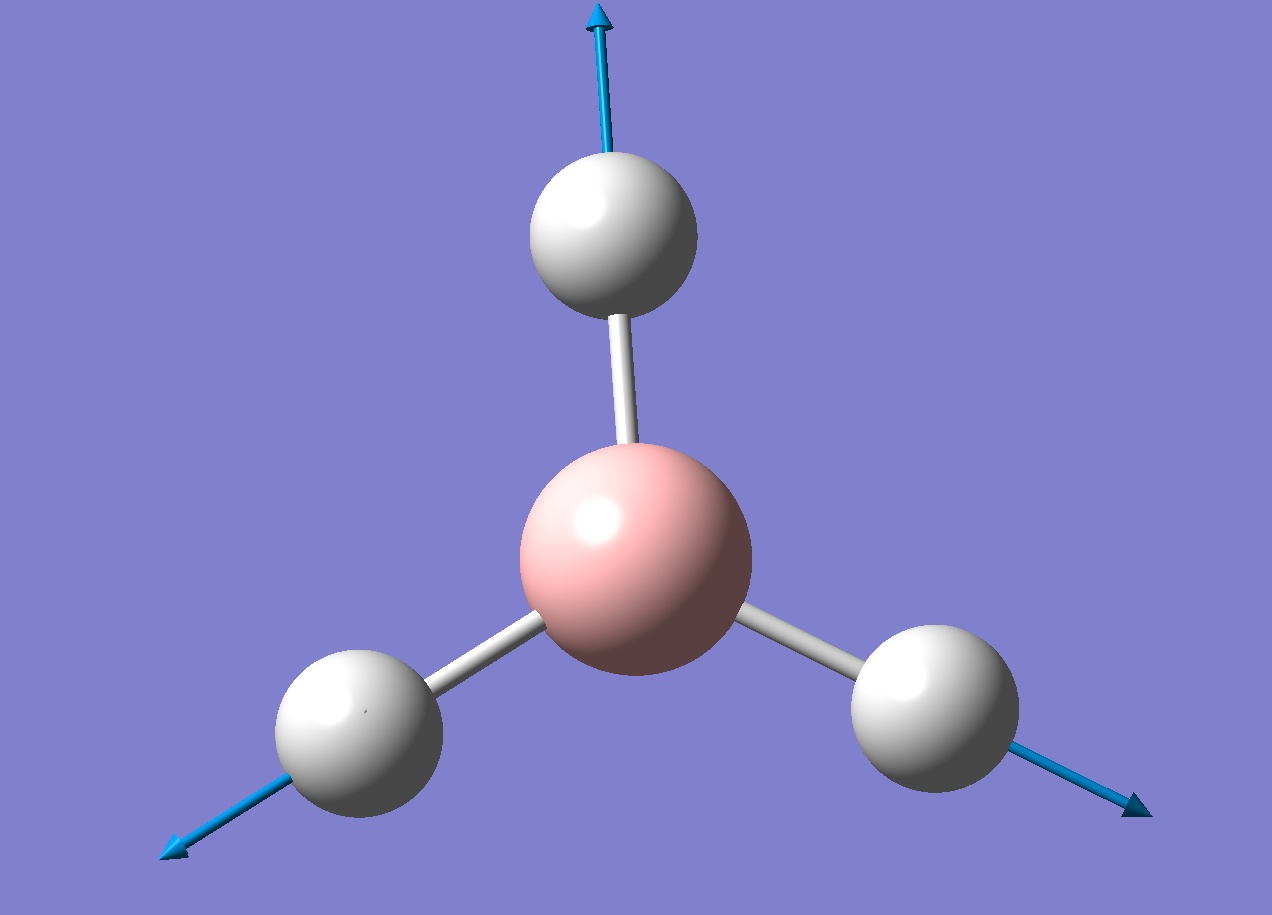
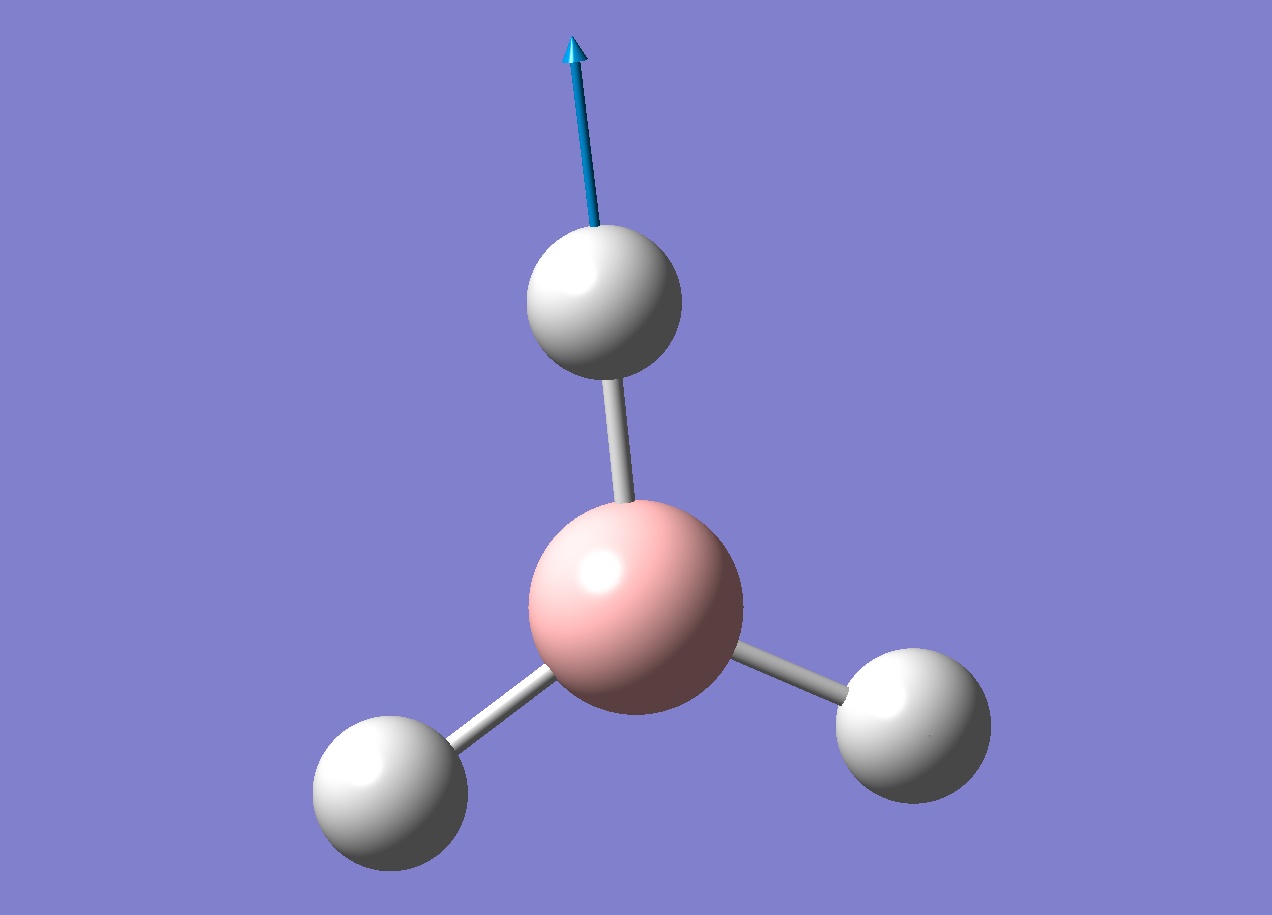
Vibrational Analysis of BH₃

A frequency analysis was run on the optimised borane molecule to find the 6 vibrations of borane (note that there are six because of the 3n-6 equation). Each vibration is shown below in the table.

Frequency	Intensity	Symmetry Label	Diagram
1145.71	92.6991	A2	Symmetric bend of all hydrogens, boron remains stationary
1204.66	12.3789	E'	Antisymmetric bend of two hydrogens
1204.66	12.3814	E'	Symmetric bend of two lower hydrogens with antisymmetric bend of upper hydrogen
2592.79	0	A'1	Symmetric stretch of all hydrogens
2731.31	103.837	E'	Antisymmetric stretch of two lower hydrogens
2731.31	103.83	E'	Symmetric stretch of lower hydrogens with antisymmetric stretch of upper hydrogen

Looking through the log file showed two lines labelled "low frequencies". The first line had values that were much lower than the second line, these are the vibrations of the centre of mass of the molecule and should be 0 if the calculation were perfect. The largest "0 value" in this case is 21.4975 which is two orders of magnitude smaller than the first non 0 value (1145.7148), suggesting the calculation is fairly good. With a better basis set these values would be closer to 0.

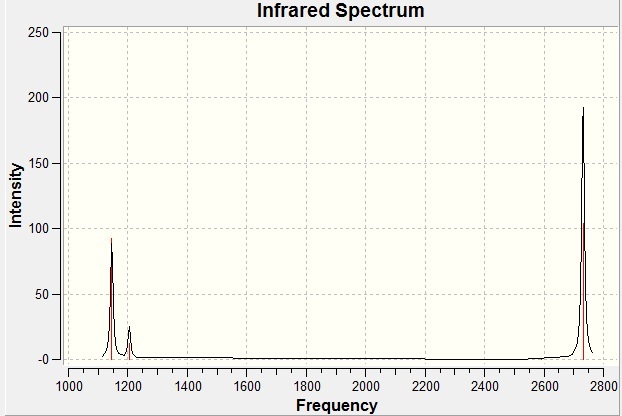
An infra-red spectrum would show which vibrations are optically active. Since there are six vibrations we could conclude that there will be six peaks, however looking at the IR spectrum (below) shows only three peaks.

There are two pairs of degenerate vibrations that will result in the same peaks (1204.66 and 2731.31cm^-1) which would result in four peaks but this does not explain why the 2592.79cm^-1 vibration does not show a peak. This vibration is completely symmetric, this means there is no overall dipole as all the stretches will cancel each other out. Since there is no overall dipole the IR spectrometer has no way of measuring this vibration and as such it will not show up on an IR spectrum (the intensity will be 0). This results in only three peaks being present.

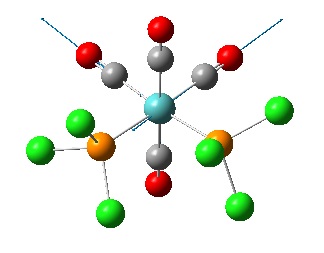
Cis and Trans Isomerism of Octahedral Mo Complexes

The cis and trans isomers of Mo(CO)₄(PCl₃)₂ were drawn using Gaussview and minimised using DFT/B3LYP and the LANL2-MB basis set. Note that the real world molecule actually has phenyl groups instead of chlorides, this substitution has been made to reduce computing time as phenyl groups are larger and will therefore take more time to optimise. This may seem at first like a strange substitution but for the sake of this calculation chlorides are fairly similar to phenyl groups in terms of electro-negativity, so will have a similar effect on the computed bonds but will take much less computer time. LANL2-MB is a simple basis set (MB stands for minimal basis) so will only give approximate results but will take relativity less time to compute. The PCl₃ groups were rotated as in the instructions and then the molecule was optimised again using LANL2-DZ, a better basis set (DZ stands for double zeta). This gave the molecules below.

cis isomer: http://hdl.handle.net/10042/to-5281

trans isomer: http://hdl.handle.net/10042/to-5282

The trans isomer appears not to have any bonds between the P and Cl, this is in fact not the case and is due to what Gaussview views as a bond. If two atoms are too far from each other, Gaussview will not draw a bond between them. This does not mean there isn't one, only that the bond distance is larger than some pre-set distance (organic bonds tend to be shorter than inorganic). Obviously a bond isn't just a line between two atoms that is either there or not there, it is in fact an area of space between (and around) two (or more) atoms that either share, donate or accept electrons from each other and in doing so lower their overall energy. The lines that we draw to represent these bonds are simply a means of visualising them and in fact do not describe them very well. Gaussview will only draw lines between atoms that are under a set distance from each other, if there is no line this does not mean there will not be a bond in reality.

LANL2DZ is better than LANL2MB, but for phosphorus it is still a minimal basis set. D orbitals are not included so the hyper-valency of the phosphorus is not considered which may lower the accuracy of the calculation. To increase the accuracy the text file must be changed before submitting the molecule again to SCAN, this was done as in the instructions by adding "extrabasis" to the line containing the basis set data and

(blank line)

P 0

D 1 1.0

0.55 0.100D+01

(blank line)

to the bottom of the file. This tells the programme to add a phosphorus with d orbitals of a certain width to the calculation. The new, more optimised files were used in the frequency calculations, before submitting to scan the above code was again placed in the log file to keep the basis set and pseudo potential the same.

The cis isomer was found to have 4 vibrations of the C=O bonds while the trans was found to have 2, however they were found to be degenerate. There were also two more vibrations for the trans isomer but these were at very small intensity (~5) so have not been included. A table of the results is shown below along with diagrams showing the vibrations of the two molecules as displacement vectors. It is rather difficult to see but the background has been changed to white to try and make it clearer, the displacement vectors are the thin blue arrows.

Cis and Trans vibration frequencies

Trans vibration frequencies	Cis vibration frequencies
1939.18 (degenerate)	1938.57
1939.89 (degenerate)	1941.51
	1952.53
	2019.43

1939.18cm^-1 1939.89cm^-1

Notice that the two degenerate vibrations are very similar, two carbonyls vibrate anti to each other on two different axes. It is probable that the frequencies (and therefore the energies) of the two vibrations are slightly different because the calculation is run on a rigid molecule where the position of the Cl will influence the carbonyl vibrations. In a real molecule (>0K) the Mo-P bond could rotate and the two vibrations would be exactly equivalent. This is why the vibrations have been described as degenerate. The four vibrations of the cis carbonyls are:

1938.57cm^-1 1941.51cm^-1

1952.53cm^-1 (asymmetric)2019.43cm^-1 (symmetric)

The free CO vibrational frequency is 2143cm^-1 but when coordinated to a metal the stretching frequency is lowered by an amount that depends on the extent of backdonation. This means a larger amount of backdonation will result in a lower wavenumber and as such we can see which carbonyl experiences the most. The trans isomer carbonyls all experience the same degree of backdonation as can be seen by their equal wavenumbers. The cis carbonyls however have different degrees of backdonation since they are not in the same environment, with the carbonyls that vibrate with a higher wavenumber (on the diagram the ones pointing left and right with wavenumber 1941.51cm^-1) experiencing less backdonation than the other two. This is could be due to the phosphorus group which has a large structural trans effect which would be expected to lengthen the trans CO bond, lowering it's energy which would also lower it's wavenumber. This does seem to explain the difference in the vibrational wavenumbers but it should be noted that this explanation is mainly for square planer complexes so may not be entirely accurate for this example. The quoted literature actually goes into some detail explaining the differences in square planer and octahedral transition metal complexes regarding the trans effect. It explains how in octahedral complexes the cis effect (like the trans effect but for cis ligands) can actually be equal or even larger in intensity than the trans effect. For this reason it is difficult to say with confidence that the difference between the vibrations of the carbonyls is due to the trans effect. It would be interesting to see the effects of removing two carbonyl groups from this molecule to give a square planer complex to see experimentally how the CO frequencies change, however it may be difficult to get the square planer complex rather than the tetrahedral. A way around this would be to use computational methods, this could be done in this lab if more time were allocated.

Optimising a 10 atom Gold Cluster and Comparison of Ions

Gold clusters of small number of atoms normally adopt planar conformations. To see why this is the case the planer structure of the lowest energy Au₁₀ cluster according to the literature was optimised as well as the lowest energy 3D structure. The method used was DFT/B3LYP and the basis set was LANL2DZ. This basis set must be used in this case because 3-21G is only available up to Xenon. The LANL2DZ pseudo-potentials used are very good approximations for gold as the valence electrons move so fast (0.5 speed of light) which means making the assumption that all the Coulumbic potential terms for non valence electrons (core electrons) can be replaced with an effective potential in the Shrödinger equation is fairly accurate since the core electrons move slowly compared to the valence electrons. The relitivistic effect is also included which further increases accuracy. Ionic effects were also considered by changing the charge on the planer complex to +1 and -1. The models of the neutral molecules were drawn on gaussview 5.0 by adding 1 atom at a time and then adjusting the bond angle and length to put the new atom in the correct place before repeating the process. This worked very well for the 2D structure as the molecule is basically lots of connected equilateral triangles and worked still fairly well for the 3D structure which also contains many equilateral triangles. The bond angle therefore was 60^o in most cases and the bond length was initially set to 2.47Å which is the literature value for the experimental bond length of Au₂. Jmols of the 2D and 3D structures are shown.

http://hdl.handle.net/10042/to-5390

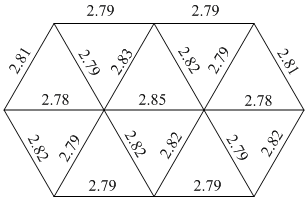
The most notable thing about the optimised molecule is that the middle bond has disappeared. As discussed above, this does not mean the bond is not there but simply that it is longer than the others. The bond has been left out to show that this is longer than the rest, this idea has been used throughout the project (with the exception of the 3D structure that contained many "long" bonds) to show how the bond lengths have changed to allow easy comparison. A diagram showing the bond lengths is shown below.

Au₁₀ bond lengths

The bond lengths in the optimised molecule are longer than the bond length of Au₂. The bond lengths are actually closer to the bond length associated with an aurophillic bond (2.7-3.3Å). This is a bond that is similar to a hydrogen bond and occurs because of the single s electron of gold. This is not the type of bonding in this molecule however as this only occurs in Au(I) complexes, not elemental gold (oxidation state 0). Since this cannot explain the bond lengths it is unclear why they should be so much longer than Au₂. The bonds are definitely there, since the Van der Waals interactions would be much longer (3.7Å) but the

The atomic charges of the molecule were calculated and are shown below.

These charges show that most of the electron density is around the outside of the molecule to the left and right. The literature reports that a similar structure of Au₁₀ reacts with carbon monoxide around the outside of the molecule which leaves the electronic structure of the middle of the molecule relatively unchanged. This structure is likely to be similar. It also suggests that the HOMO is largest around these areas, a MO analysis has been carried out later to see if this is correct.

An optimisation was then run for the 3D structure.

http://hdl.handle.net/10042/to-5397

Note that bonds have been drawn in to the 3D structure to make it look more like the literature picture. The 3D structure shown above is fairly similar to that shown in the literature but is not exactly like it. This is because a different method was used (DFT rather than MP2), the literature reports that DFT tends to favour 2D complexes which is what has happened here. The optimised structure could be changed slightly and the calculation run again but this was not run due to the fact that the first optimisation of the 3D structure took 4hour 55minutes compared to 44 minutes for the 2D structure. Further optimisation of the 3D structure was therefore considered to be an unnecessary use of computer time and was not performed. The structure given above is still interesting however, it shows how gold does indeed prefer to be 2D in small clusters. In fact this 3D structure can be considered two 2D structures on top of each other as shown below.

Au₁₀ (3D) bond lengths

The bond distances between the two levels (inter-layer) are higher than the distances of atoms in the same level (intra-layer). This suggests having multiple layers is less stable than having all atoms in the same level, thus the 2D structure is predicted to be more stable. The bonds also seem to be shortest (and therefore strongest) when involved in an equatorial triangle, again supporting the 2D structure above.

The Au₁₀^- cluster was then considered to see the effects of ionisation.

http://hdl.handle.net/10042/to-5398

This structure has it's shortest bonds horizontally across the molecule. This was surprising as the longest bond in the neutral complex is now one of the strongest. This means this bond has actually been strengthened by the addition of an electron which means we can then infer that the LUMO of the neutral complex must be a bonding orbital around the middle Au-Au bond.

Au₁₀^- bond lengths

The bond lengths show that the middle bond is now the strongest and that the bonds between the "lines" are the weakest. This suggests a LUMO where the combined atomic orbitals are bonding down a horizontal line but antibonding between lines. This would result in the observed change in bond lengths if the complex were made anionic.

The Au₁₀⁺ cluster was then analysed to see what happens when an electron is removed from the neutral complex. A jmol is shown with a diagram showing bond lengths below that.

http://hdl.handle.net/10042/to-5399

Au₁₀⁺ bond lengths

The bond lengths in the cation are generally longer than those in the neutral complex. This suggests the molecule has been destabilised by the loss of an electron. The two bonds that have disappeared have been especially destabilised, going from 2.78Å to 2.88Å. The HOMO is therefore most likely to be a bonding one across these bonds, as removing an electron has had the biggest destabilising effect here.

To see if the hypotheses formulated about the HOMO and LUMO from the ion bond lengths were correct, a molecular orbital calculation was run. This proved problematic as the basis set used (LANL2-DZ) seemed to have some problems involved with the format checkpoint file output and the 6-31G basis set could not be used as it wouldn't work for gold. To overcome this the GEN basis set was used as well as some code specific for gold from basis set exchange. The calculated HOMO and LUMO are shown below.

HOMO LUMO

The LUMO is as expected, bonding horizontally across the molecule but antibonding up and down it. This is in agreement with the conclusions made from analysis of the Au₁₀^- bond lengths. Notice that the middle bond has been stabilised the most because there is a large bonding interaction between the two atoms while the bonds left and right of this will be stabilised less since there is less interaction along this bond.

Also, the HOMO is in agreement with the conclusions from the Au₁₀⁺ bond lengths (the orbital is bonding along the bonds that have been desabalised most by the removal of an electron). However there is not a large interaction along these bonds so it is likely that something else has occurred to destabilise them further. The middle bond is antibonding in the HOMO. This means the removal of an electron from this orbital will stabilise this bond, making it shorter. This could have the effect of further stretching the bonds either side of it, resulting in them being even more destabilised. The conclusions from the atomic charges also appear to be correct, with the HOMO being largest about those atoms that have the lowest charge (~-0.14Debye).

The HOMO-2, HOMO-1, LUMO+1 and LUMO+2 were then analysed to see what would happen if more electrons were removed from or added to the cluster.

HOMO-2 HOMO-1

If a second electron were removed the original HOMO would be completely empty and the bond lengths would change in a similar way in which they did when the first electron was removed, since the second will be removed from the same orbital. The third electron would be removed from the HOMO-1 to give Au₁₀³⁺. This would destabilise the bonds that are bonding in this MO, namely the middle and extreme left and right bonds. This may be possible looking at the relative energies of these two orbitals (-0.234AU for the HOMO-1 and -0.232AU for the HOMO) which are very close. The HOMO-2 is slightly further away in energy (-0.271AU) so would be less likely to lose an electron, but if it did this would destabilise the upper and lower parts of the molecule that experience bonding from this MO.

LUMO+1 LUMO+2

If electrons were added to the LUMO+1 much of the molecule would be destabilised due to the large amount of antibonding character in this MO. There doesn't seem to be any bonding interactions between atoms with most of the electron density on the extreme left and right atoms in what appear to be formed from s orbitals although this is hard to be sure of because of the large number of occupied orbitals of gold. The LUMO+2 is much the same story with very few bonding interactions. This suggests it would take a lot of energy to add more than two electrons to Au₁₀ as this would start putting electrons in these orbitals.

This mini-project has shown the effects of ionisation on a 10 atom gold cluster and has explained them using bond lengths, atomic charges and molecular orbitals. An effort was also made to explain why a 2D structure was adopted in favour of a 3D structure but due to difficulties with the optimisation of the 3D structure and time constraints was only slightly successful. The MO analysis was however quite good and supported ideas that were formulated earlier from charges and bond lengths. If more time were allotted then the 3D structure as well as more structures (3D and 2D) would be optimised. It would also be interesting to see how different sizes of cluster behave, this would also be looked into.