Rep:Mod2:cathyleeinorganic

Module 2

Analysis of BCl₃

BCl₃ molecule

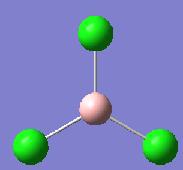
The method to calculate the optimisation of BCl₃ was DFT B3LYP. This tells the programs the different approximations it should use in the Schrodinger approximation.

Basis sets are a set of functions used to determine the molecular orbitals of a molecule. The more basis sets used will allow a more accurate representation of the MO but the calculation would take a very long time. Therefore, the basis set used was LanL2MB, which is a medium level set of function (won't take too long too work out but the results are reltively accurate). This calcualation took 14.0 seconds to run.

Same method is needed because the same approximations need to be applied in order for the calculations to be comparable to each other. Using different asumptions will lead to different results. The same applies for the basis set, it is to do with how accurate the results will be. The current basis set being used is a medium level one, if two different ones are used then the calculations would have different accuracies and results may not be able to correspond to each other.

Frequency analysis is carried out to ensure the optimised molecule is indeed the most stable conformer. If all the frequencies are positive then the lowest energy is achieved.

Some bonds are not shown after completing a calculation. This does not mean that the bond does not exist but what it is the program believing that the bond is "too long" to exist. Gaussian has set bond lengths for each bond and if goes over that it expects the the "bond" does not exist. The two main types of bond that we need concern are ionic and covalent bonds. The bonds represent the electronic interactions between two atoms. If they are far away then the bond is weak because the nuclei and electrons are far apart to interact.

Results

• B-Cl bond length = 1.87A Literature Value = 1.75A
• Cl-B-Cl bond angle: 120 degrees
• Point Group: D_3h

The bond angle of BCl₃ of 120 degrees corresponds to the bond angle expected of the trigonal planar molecule.

Symmetry elements of BCl₃ are C₃, 2C₂, σ_h and σ_h and from using the point group flow chart, this assigns BCl₃ with the point group D_3h which corresponds to what Gaussview predicted.

Analysis of BH₃

MO Diagram of BH₃

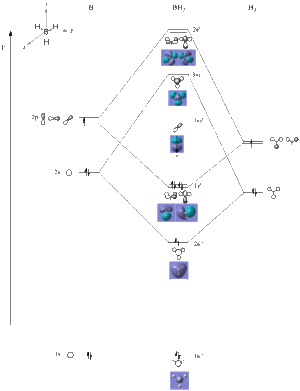
All the occupied molecular orbitals (MO), the non-bonding orbital and the σ^* orbital were very accurate to linear combination of atomc orbitals (LCAO).

The π^* orbitals do not show huge similarities to the LCAOS. This suggest that the calculations are still approximations and some assumptions are made so not everything will be correct but most results will be accurate. This is expected because the basis set used is 3-21G which is a relatively low accuracy causing the MO not to be similar to the LCAO. However, the nodal planes in LCAO do correspond to what is seen in the molecular orbital.

Analysis of an Organometallic Complex

Structure and Stability of Mo Complex

• Total Energy of Cis Complex = -1637201kJmol^-1
• Total Energy of Trans Complex = -1637199kJmol^-1
• Difference in Energy = 2kJmol^-1

The molecule with the lowest energy would be the most stable complex. The cis complex is therefore the most stable complex. It would be expected that the trans would be more stable due to the steric reasons. In the cis molecule you would expect there to be steric clash between the Cl on the PCl3 groups. However, the Cl groups are relatively small so the steric clash will be very minor, if the groups were larger, say phenyl groups, it would be expected then the trans to be more stable.

The energy difference between the two complexes is very small. This suggests that the groups make little difference to whether the groups are in cis or trans position.

Analysis of Vibrations

	P-Mo-P Stretch	P-Mo-P Stretch	C=O Stretch	C=O Stretch	C=O Stretch
Cis Mo Complex
Vibrational Frequency	321	348	1806	1807	1873
Infrared Intensity	412	168	673	1317	679
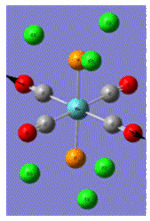
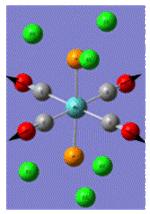
Trans Mo Complex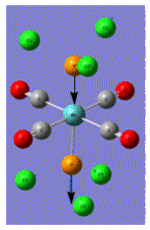
Vibrational Frequency	409		1906	1951	2031
Infrared Intensity	727		1475	1467	4

Both molecules have positive frequencies (lowest cis conformer frequency = 60cm^-1, lowest trans conformer frequency = 5cm^-1), suggesting that the optimised molecules are indeed at the the minimum energy. A vibration at a very low frequency suggests that it has a very low energy so at room temperature this vibration will be very small.

According to literature values, the carbonyl frequencies should be found around 1900 - 2000cm^-1. The trans complex coniside with these numbers but the cis does not. However, it is relatively close and is probably due to the PCl₃ groups lowering the frequency. However, the same number of bands do appear although slightly shifted.

Mini Project

Ammonia Borane Conformers

Introduction

Many believe that hydrogen is the fuel of the future. The storage of hydrogen is difficult, so scientist have come up with the compound ammonia borane (NH₃BH₃ as a molecule with many sources of hydrogen that is stable at room temperature. Ammonia Borane decompose to release hydrogen and the byproduct borazine:

• NH₃BH₃ --> B₃N₃H₆ + 3H₂

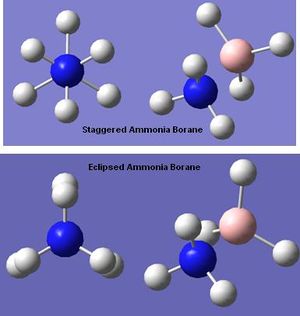
Structure of Ammonia Borane

• Ammonia Borane Staggered Energy = -217305kJmol^-1
• Ammonia Borane Eclipsed Energy = -217300kJmol^-1
• Difference in Energy = 5kJmol^-1

The staggered conformer has the lowest energy so it is the most stable, suggesting that this is the favoured conformer which correspons to literature data . The eclipsed conformer is expected to be higher in energy because the slight steric hinderance of the hydrogens. The energy difference is relatively small because the hydrogens are small groups and the N-B bond is quite long (eclipsed N-B = 1.68A, staggered N-B = 1.71A).

• Ethane Staggered Energy = -208465kJmol^-1
• Ethane Eclipsed Energy = -208455kJmol^-1

Ethane has a higher energy than ammonia borane because C-C bond length is shorter than N-B bond (staggered C-C = 1.54A, eclipsed C-C = 1.56A) so the steric hinderance caused by the hydrogens will be greater increasing the energy of the overall molecule.

Since the N-B bond length is longer, this suggests that the bond is weak so is therefore more reactive. This means that hydrogen will be released better when compared with ethane.

The melting point of ammonia borane is 110°C whereas ethane melting point is -181.76°C. Even though the ammonia is isoelectronic to ethane, the difference in the two melting points is very large. Ammonia borane has a dipole moment of 5.83 debyes and because of this, the molecule will arrange itself in a lattice. The lattice is stabilised by the di-hydrogen bonds between B-H----H-N.

Formation of Ammonia Borane

• NH₄Cl Energy = -1351728kJmol^-1
• NaBH₄ Energy = -1351729kJmol^-1
• NH₄BH₄ Energy = -220229kJmol^-1

• NH₄Cl + NaBH₄ --> NH₄BH₄ + NaCl
• NH₄BH₄ --> NH₃BH₃ + H₂
  • E(reactants)-E(products) = 113kJmol^-1

The overall decomposition to produce ammonia borane is lower in energy compared to the reactants. This implies that the reaction is energetically favourable.

Comparing the energies, NH₄BH₄ is slightly ,lower in energy compared to NH₃BH₃ (difference of 2924kJmol^-1).