Rep:Mod2:SBen

Module 3

The Cope Rearrangement

The Cope rearrangement of 1,5-hexadiene is a [3,3]-sigmatropic shift rearrangement. The objective of this section of the investigation is to locate the low-energy minima and transition structures on the C6H10 potential energy surface which will enable determination of the perferred reation mechanism. There have been a number of studies, both experimental and computational, into this rearrangement and there has been a large amount of discussion regarding the mechanism. It is now widely accepted that the reaction goes via a concerted transition state, the two possible transition state structures are the "chair" and "boat" structures as shown below. The "boat" transition structure is the higher energy of the two..

Cope rearrangement

Chair Transition State	Boat Transition State

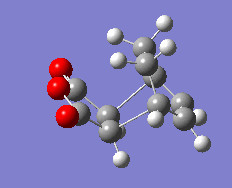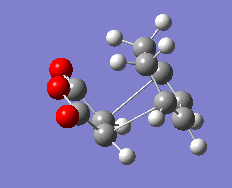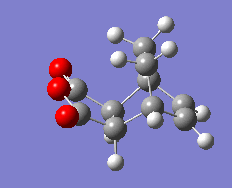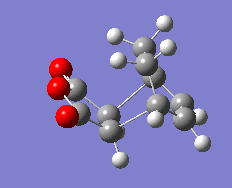
Initially, a range of conformers of 1,5-hexadiene were drawn in Gaussview and optimised at the HF/3-21G level of theory. Table 1 shows the low energy conformers that were found along with their point group and energy after optimisation. The low energy conformers found have identical energies to those in the tutorial appendix. The lowest energy conformer found corresponds to the gauche 3 conformer.

Table 1. Conformers of 1,5-hexadiene

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G	Relative Energy/kJmol-1
Anti	Anti structure	C2	-231.69260	0.2
Gauche	Anti structure	C2	-231.69153	3.0
Low Energy	Anti structure	C1	-231.69266	0.0
Anti 2	Anti structure	Ci	-231.69254	0.3

The anti 2 conformer was then optimised at the B3LYP/6-31G* level. The energy of the anti 2 conformer was found to be -234.61171 a.u. at this higher level of theory, this is 7664.3kJmol^-1 lower than the energy found at the HF/3-21G level of theory. There were also differences found in the overall geometry of the anti 2 conformer when it was reoptimised at a higher level of theory, some of these geometric differences are displayed in the table 2. They are compared with values found in computational studies in literature. with reasonable success.

Table 2. Comparison of geometric data found at different theory levels

Geometric Feature	HF/3-21G	B3LYP/6-31G*	Literature
C1=C2 bond length	1.316 Å	1.333 Å
C2-C3 bond length	1.509 Å	1.504 Å
C3-C4 bond length	1.552 Å	1.548 Å	1.535 Å
C1-C2-C3-C4 dihedral angle	114.63°	118.53°	115.9°(-64.1°)
C3-C4-C5-C6 dihedral angle	114.63°	118.53°	115.9°
C2-C3-C4-C5 dihedral angle	180.0°	180.0°	180.0°

A frequency analysis of the optimised Ci anti 2 conformer was run at the B3LYP/6-31G* level, all vibrational frequencies were found to be real and positive, confirming that a minimum energy had been found. The IR spectrum is shown here. The results from the frequency analysis also give a list of energies which are tabulated below, in table 3.

IR spectrum of the Anti 2 conformer of 1,5-hexadiene

Table 3. Energies

Sum of electronic and zero-point energies	(E = Eelec + ZPE)	-234.46920 a.u.
Sum of electronic and thermal energies	(E = E + Evib + Erot + Etrans)	-234.46186 a.u.
Sum of electronic and thermal enthalpies	(H = E + RT)	-234.46091 a.u.
Sum of electronic and thermal free energies	(G = H - TS)	-234.50078 a.u.

Optimising the "Chair" and "Boat" Transition Structures

In this section different methods were used to set up and perform a transition structure optimisation. The reaction coordinate was visualized and an IRC (Intrinisic Reaction Coordinate) analysis run. Calculation of the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures was also possible.

Chair Transition Structure

An allyl (CH₂CHCH₂) fragment was drawn in Gaussview and optimized at the HF/3-21G level. Two allyl fragments were then placed next to each other so they looked like the chair conformation, with a 2.2 angstrom gap between the terminal ends of the fragments. This "guess" structure was then optimised in two different ways; optimisation to a TS (Berny) and the frozen coordinate method.

Transition state optimizations are often more difficult than minimizations because the calculation needs to know where the the reaction coordinate is. Here we can use the TS (Berny) method of optimization as we have a good guess for the transition structure geometry, so we can easily produce this information by computing the force constant matrix, or "Hessian". This is then updated as the optimization proceeds. The other method used is the frozen coordinate method in which a better transition structure can be generated by freezing the reaction coordinate and minimising the rest of the molecule. Once the molecule is fully relaxed, the reaction coordinate can then be unfrozen and the transition state is optimized again. One advantage of using this method, is that it is not always necessary to compute the whole Hessian, and simply differentiating along the reaction coordinate may give a good guess for the initial force constant matrix. The frozen coordinate method can save a considerable amount of time in cases where the force constant calculation is expensive.

The frequency calculation gave and imaginary frequency of -818cm^-1 with both methods, as expected. This vibration has been animated below for the TS (Berny) method. The animations follow what would be expected in the Cope rearrangement.

The energy of the transition state was found to be the same for both methods at -231.61932 a.u. The distance between the terminal ends of the allyl fragments was found to be 2.02045 Å using the TS (Berny) method and 2.02044 Å using the frozen coordinate method. These can be said to be the same as the differences are outside the accuracy of the methods used.

Boat Transition Structure

The boat transition structure was optimised using the QST2 method. In this method, the reactants and products for the reaction are specified and the calculation interpolates between the two structures in order to find the transition state between them. Initially, the job failed so the reactant and product structures were altered to resemble the boat transition state, as shown to the right, and a QST2 calculation was performed again. This time the job converged and one imaginary frequency was calculated at -840cm-1, this has been animated. The energy of this transition structure was found to be -231.60280 a.u. and the distance between the terminal ends of the allyl fragments was 2.14Å.

Intrinisic Reaction Coordinate (IRC) Analysis

The IRC method you to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. It creates a series of points by taking small geometry steps in the direction where the gradient of the energy surface is steepest. The aim is to find out which conformers of 1,5-hexadiene the transition structures lead to. Intially, the IRC job was run for both the boat and chair structures with the force constant calculated at the begining of the calculation and the number of points along the IRC was set to 50. The energies found in this IRC calculation were -231.61932 a.u. for the chair structure and -231.67507 a.u. for the boat structure. These are not minimum energies and the total energy plots show that minima had not yet been reached with 50 points. This left a few possible options to complete the IRC analysis; the method chosen was to take the last point on the IRC and run a normal minimization. After optimisation of the last point on the IRC of the chair structure the energy was -231.69167 a.u. this corresponds to the gauche 2 conformer of 1,5-hexadiene which is shown in the tutorial appendix. Optimisation of the last point on the IRC of the boat structure gave an energy of -231.68303 a.u. this does not correspond to any of the low energy conformers of 1,5-hexadiene, to find a minimum for the boat structure it may necessary to improve the IRC method used, possibly by increasing the number of points calculated in the IRC and optimising again after that.

Activation Energies

Starting from the HF/3-21G optimized structures, the chair and boat transition structures were reoptimised using the B3LYP/6-31G* level of theory. The following tables display and compare some of the properties found in these calculations at both levels of theory. It can be seen that the level of theory has little effect on the geometry of the structures but there is a noticable difference in the energies.

Chair transition state
Theory Level	HF/3-21G	B3LYP/6-31G*
Energy (a.u.)	-231.61932	-234.55698
C-C-C bond angle (°)	120.5	120
Fragments bond distance (Å)	2.02	1.97
C-C bond length (Å)	1.39	1.41
Imaginary frequency (cm-1)	-818	-566

Boat transition state
Theory Level	HF/3-21G	B3LYP/6-31G*
Energy (a.u.)	-231.60280	-234.54309
C-C-C bond angle (°)	121.6	122.3
Fragments bond distance (Å)	2.14	2.21
C-C bond length (Å)	1.38	1.39
Imaginary frequency (cm-1)	-840	-530

Table. Thermochemical data compared at both theory levels

	HF/3-21G level of theory			B3LYP/6-31G* level of theory
	Electronic energy /a.u.	Sum of electronic and zero-point energies /a.u.	Sum of electronic and thermal energies /a.u.	Electronic energy /a.u.	Sum of electronic and zero-point energies /a.u.	Sum of electronic and thermal energies /a.u.
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.46670	-231.46134	-234.55698	-234.41493	-234.40901
Boat TS	-231.60280	-231.45092	-231.44529	-234.54309	-234.40234	-234.39601
Reactant (anti 2)	-231.69254	-231.53954	-231.53257	-234.61170	-234.46921	-234.46186

The thermochemical data has been tabluated above, this data can be used to find the activation energies via the chair and boat transition structures. A summary of these activation energies is shown below and compared with experimental values. At both levels of theory the values computed are in good agreement with those quoted in the tutorial. It can also be seen that the higher level of theory gives results that are closer to experimental values.

	HF/3-21G		B3LYP/6-31G*		Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)/kcal/mol	45.71	44.69	34.06	33.16	33.5 ± 0.5
ΔE (Boat)/kcal/mol	55.61	54.76	41.96	41.32	44.7 ± 2.0

The results from this investigation show that the chair transition state is lower in energy this is in accordance with literature..

The Diels Alder Cycloaddition

The Diels Alder cycloaddition is an example of a pericyclic reaction in which the π orbitals of a dieneophile are used to form new σ bonds with the π orbitals of a diene. The number of π-electrons involved in the pericyclic transition state determines whether the reaction goes via a concerted stereospecific fashion (allowed) or not (forbidden). In this exercise, we will characterise transition structures of the Diels Alder reaction between ethylene and cis-butadiene and look at the shape of some of the molecular orbitals.

The Diels-Alder reaction between ethylene and cis-butadiene

Reactants

The AM1 semi-empirical molecular orbital method was used to optimise cis-butadiene and ethylene, and the HOMO and LUMO of the reactants was visualised. The results are shown in the table below.

Reactant	Molecular Orbital	Image	Energy (a.u.)	Symmetry
cis-Butadiene	HOMO		-0.3438	Anti-symmetric
	LUMO		0.01707	Symmetric
Ethylene	HOMO		-0.38775	Symmetric
	LUMO		0.05283	Anti-symmetric

For orbitals to interact they need the same symmetery, so the HOMO of cis-butadiene can interact with the LUMO of ethylene, and the LUMO of cis-butadiene can interact with the HOMO of ethylene.

Transition Structure

The frozen coordinate method was used to optimise the transition structure at the B3LYP/6-31G* level. The transition state has an envelope type structure to maximize the overlap between the ethylene π orbitals and the π system of butadiene. The starting geometry was obtained by drawing the bicyclo system, as shown in the wiki, then removing the CH₂-CH₂ fragment. The interfragment distance was set to 2.2 angstrom. The energy of the transition structure was found to be -234.54390 a.u. with one imaginary frequency at -525cm^-1, the vibration is animated below. The C-C bond forming length calculated was 2.27 angstrom. The vibration shown corresponds to the synchronous formation of two C-C bonds which is expected in the Diels-Alder reaction. MOs have also been visualised in Gaussview.

HOMO and LUMO of transition state Molecular Orbital Image Energy (a.u.) Symmetry HOMO -0.32395 Anti-symmetric LUMO 0.02317 Symmetric

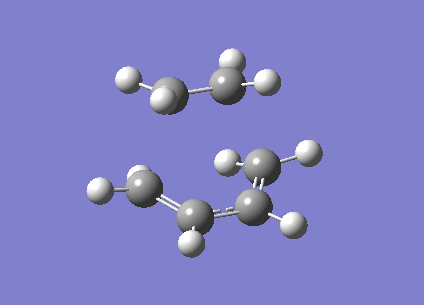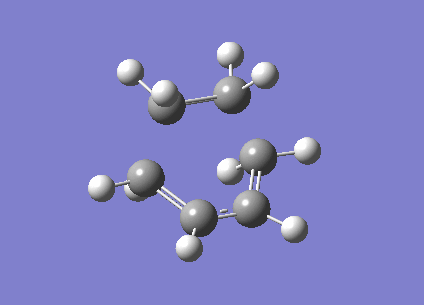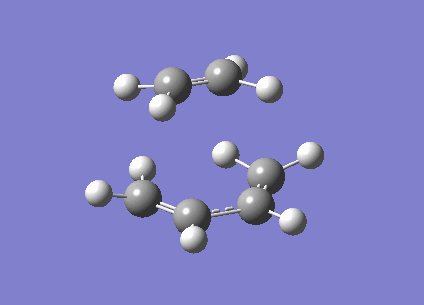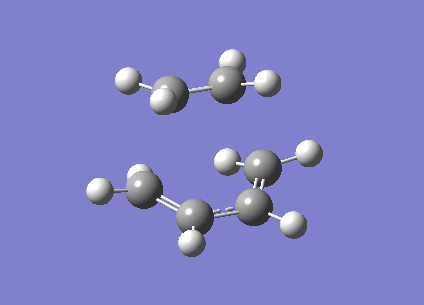
Visualisation of the molecular orbitals of the transition structure shows that the HOMO is asymmetric and therefore formed by the interaction of the asymmetric HOMO of cis-butadiene with the asymmetric LUMO of ethylene. The LUMO is symmetric and therefore formed by the interaction of the symmetic HOMO of the ethylene and the symmetric LUMO of cis-butadiene.

Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

The reaction between cyclohexa-1,3-diene and maleic anhydride is another example of a Diels-Alder reaction, but this time there are two possible products with different stereochemistry; the endo-product or the exo-product. In this section we will use computational methods to study the regioselectivity of this reaction. The table below displays the results of the transition structure optimisation.

	Exo	Endo
Product energy /a.u.	-0.15991	-0.16017
Transition state energy /a.u.	-0.05042	-0.05150
Fragment bond distance /Å	2.17	2.16
(C=O)-C-(C=O) through space distance /Å	2.2796	2.2792
C=C distance /Å	1.3968	1.3972
C-C bridge distance /Å	1.5221	1.5230
Imaginary frequency vibration /cm-1	-812	-806
Animation

The results show that the endo transition state and endo product are lower in energy than the exo transition state and product. This means that due to the kinectic control of the reaction the endo product is favoured. The lower energy of the endo transition state can be attributed to the presence of a stabilising secondary-orbital overlap, which is not present in the exo transition state.. The exo and endo HOMOs have been plotted and are shown below.

Exo	Endo
Anti-symmetric	Anti-symmetric

Conclusion

We have shown that computational methods can be a powerful tool in characterising transition structures. Here we have used different methods to successfully model transition states and locate the conformers that they lead to, as well as find transition state energies and MOs. There are however a few things that we have been unable to model in this investigation, for example solvent effects and whether a reaction is under thermodynamic or kinetic control.